喷嘴射流径向偏移斗叶对冲击式水轮机稳定性的影响
2023-12-27卿启维邓方雄李文斌邓慧铭余志顺卢加兴刘小兵
卿启维,邓方雄,李文斌,邓慧铭,余志顺,卢加兴,刘小兵*
(1. 国能大渡河革什扎水电开发有限责任公司,四川 丹巴 626300; 2. 西华大学流体及动力机械教育部重点实验室,四川 成都 610039)
水轮机的运行稳定性是一个非常复杂的综合性问题,涉及水力、机械、电气等诸多因素[1],尤其是水力因素引起的水轮机水力振动问题.水轮机水力振动与水轮机内部流动情况紧密相关;由于冲击式水轮机转轮内部流动的复杂性,近年来国内外研究者多采用数值方法开展研究.
VESSAZ[2]通过有限体积粒子法(FVPM)和流体体积法VOF模型,对冲击式水轮机内部流动进行了数值模拟研究,追踪到了水斗表面的压力变化情况;KVICINSKY等[3]将水斗固定,研究了水斗内部的压力分布.YOU等[4]采用VOF两相流模型和DOF动网格方法,模拟了冲击式水轮机飞逸过程对机组运行稳定性以及效率的影响.SANTOLIN等[5]对冲击式水轮机内射流与水斗的相互作用进行了数值研究,分析了射流形状对水轮机能量损耗以及运转效率的影响.PANAGIOTOPOULOS等[6]采用欧拉网格法进行了转轮内流动数值模拟,发现水斗背面切入射流时存在高压区,认为水斗内水流出时可能击打到后一水斗出水边背面的流动干扰会阻碍水斗转动,造成水斗水力性能下降,并采用欧拉方法与快速拉格朗日模拟(FLS)方法对冲击式水轮机数值模拟结果进行对比,研究表明FLS方法在预测转轮的水力效率方面显示出了非常好的准确性.XIAO等[7]用CFX软件进行了非定常数值模拟,分析了非定常自由表面流态和转矩随斗叶旋转的变化规律,同时研究了斗叶背面与水射流的相互作用.MACK等[8]和ŽIDONIS等[9]研究表明在射流被水斗切割过程中,水斗背面会由于相邻叶片工作面打回的射流而产生射流干扰,这种干扰会造成射流做功能力下降,从而影响水轮机运转性能.EQUSQUIZA等[10]对损坏前、损坏时和修复后监测系统测量到的振动特征进行了分析,利用模态分析技术(EMA)对转轮进行了试验研究,表明射流不对准时,动态应力分布在斗侧增加,最大应力位于裂纹出现处.肖业祥等[11]利用VOF模型对冲击式水轮机的射流流动状态进行了分析,动态分析了自由射流的变化,发现自由射流有严重干涉现象.魏鸿达[12]分析了六喷嘴冲击式水轮机内部的流动过程,找出运行中流动损失的因素.王堃[13]研究了四喷嘴冲击式水轮机内部给水机构能量损失机理,提出喷嘴能量损失主要集中在从配水环管进入喷嘴内部的不断发展的二次流中,在射流冲击转轮水斗做功的过程中,存在过量射流溢散流失现象,使得射流较多的水斗并未完全和射流进行能量转化,是做功过程中主要的能量损失点之一.曹永[14]分析了冲击式水轮机斗叶内的流固耦合及振动特性对转轮斗叶结构的影响程度,计算了不同水头段下的流固耦合特征.
目前一些冲击式水电站水轮机在安装和检修过程中,存在喷嘴射流中心线与转轮斗叶节圆发生偏移的问题,这将引起转轮内部流动变化而造成水轮机效率降低,振动加剧,影响机组安全稳定运行,甚至引起安全事故.文中针对国电大渡河吉牛水电站冲击式水轮机喷嘴射流中心线径向偏移转轮斗叶节圆的情况,采用数值方法对转轮斗叶内压力脉动及转轮受力进行研究,并实测水轮机振摆和效率情况,分析对水轮机稳定性的影响.
1 数学模型
冲击式水轮机内部流动为气液两相流动,研究中采用VOF模型方法,以便于能够更好地分析和处理复杂的气液两相界面问题.该方法中,通过引入液相体积分数C这一变量实现对计算域内相间界面的追踪,即
ρ=Cρw+(1-C)ρa,
(1)
μ=Cμw+(1-C)μa,
(2)
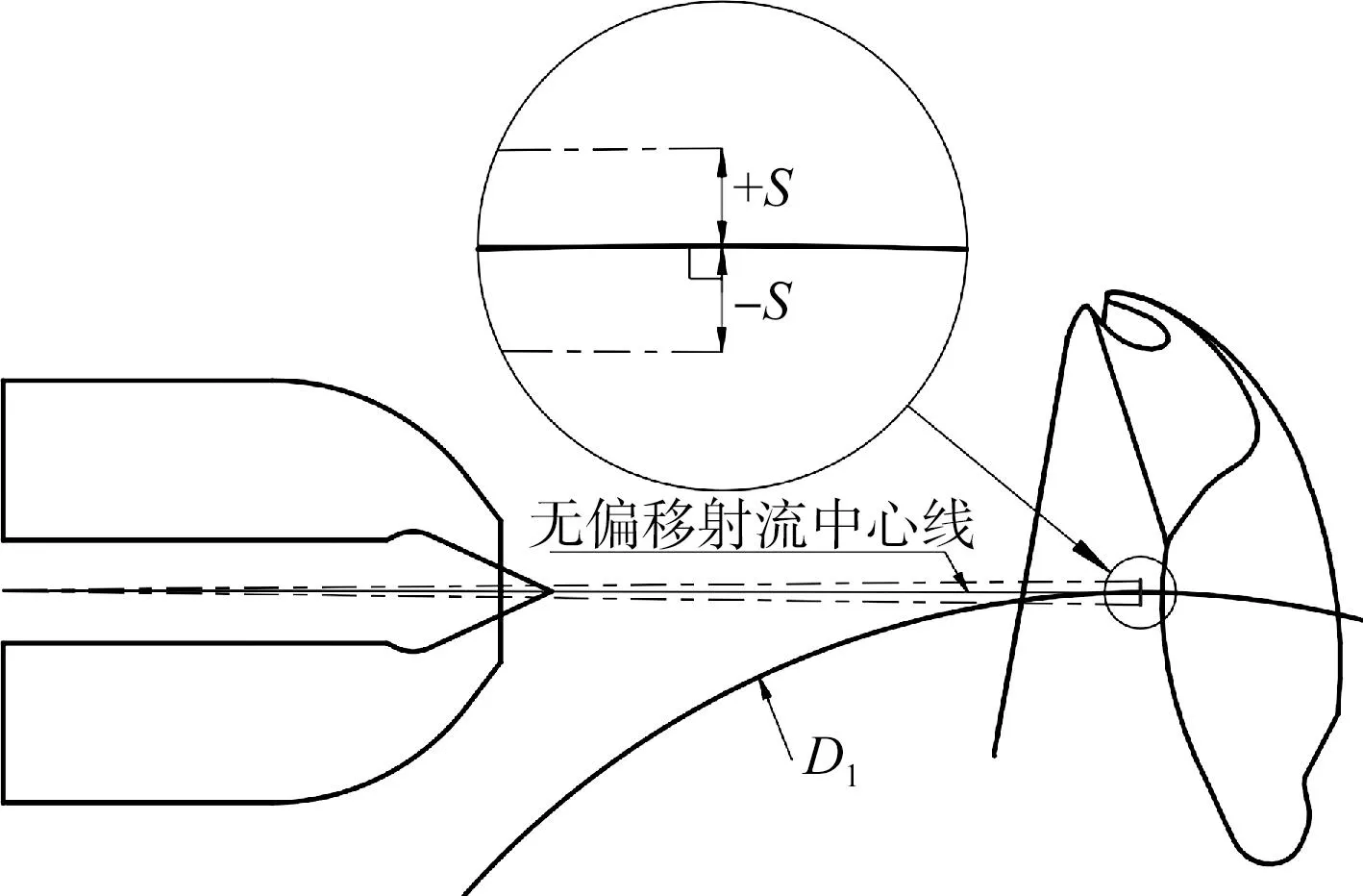
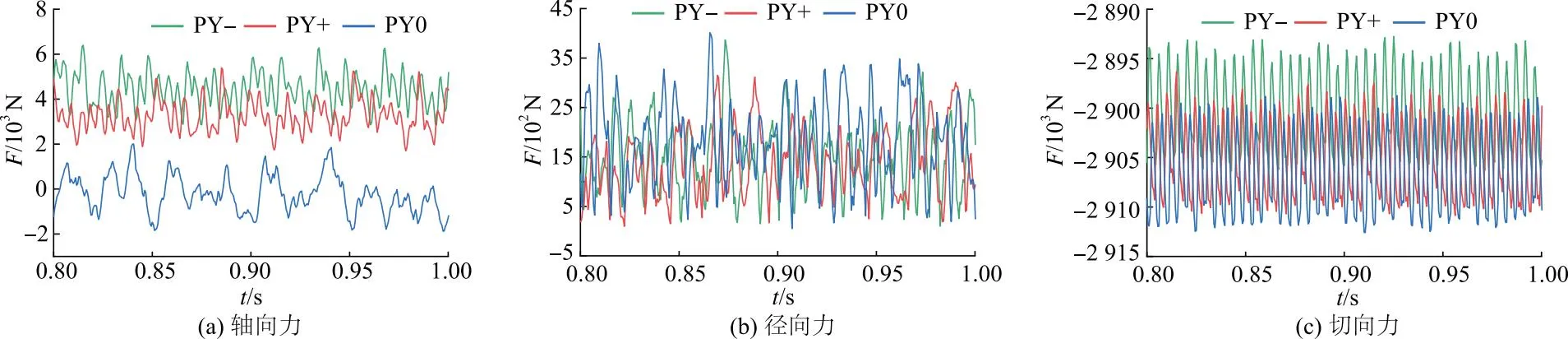
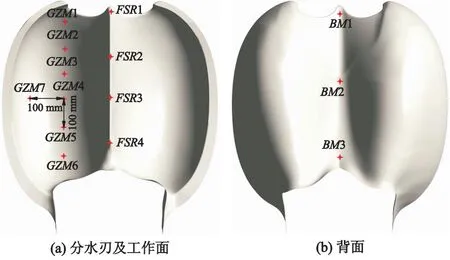
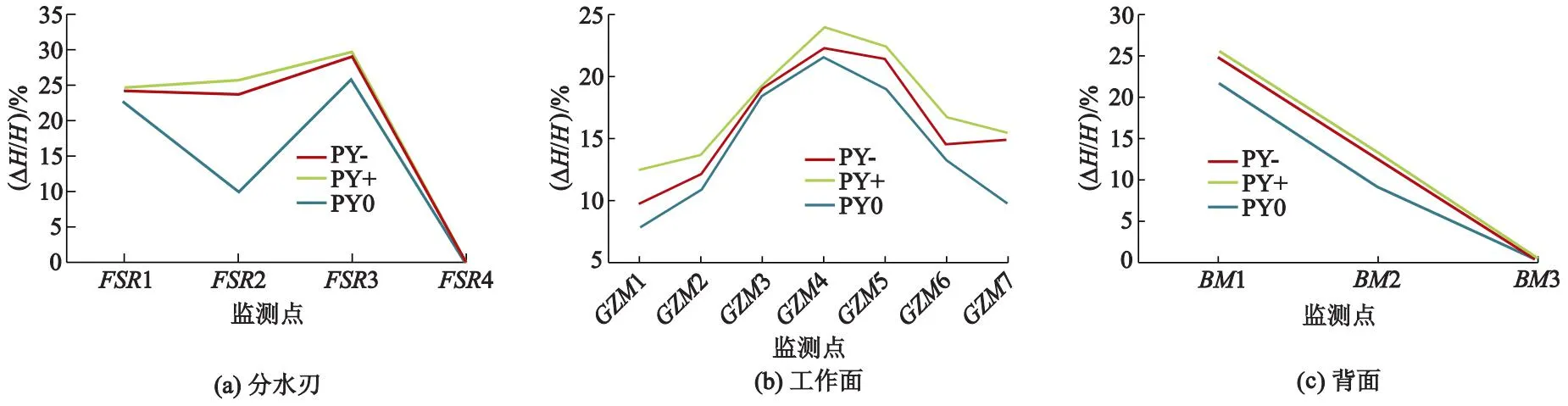
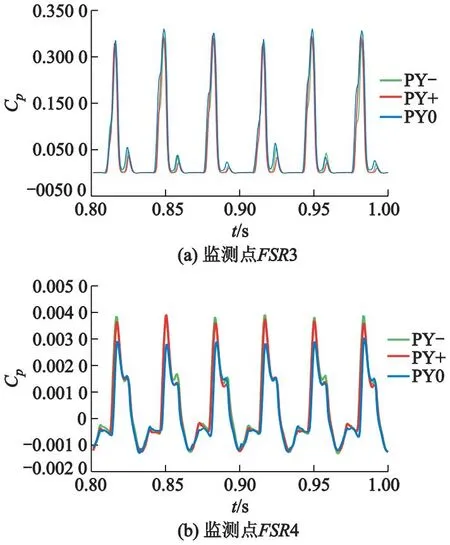
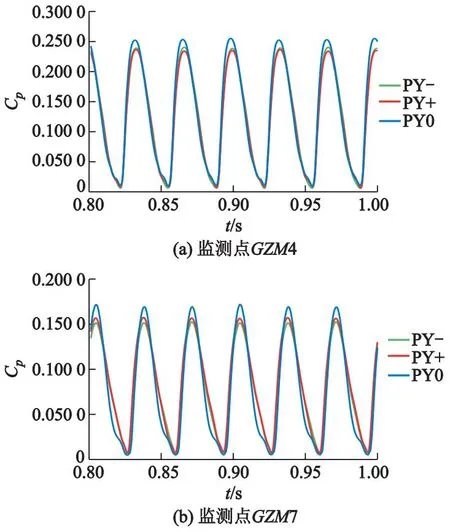
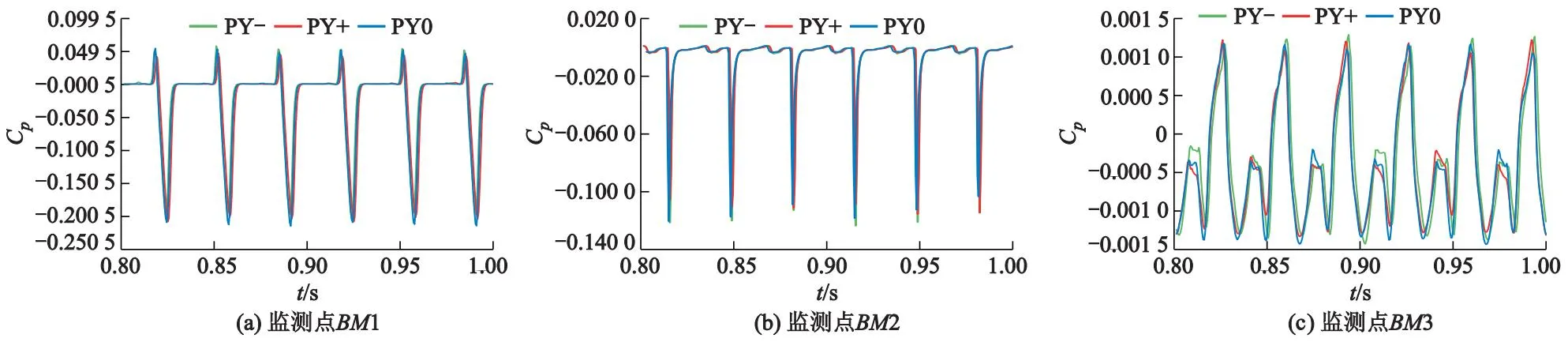
式中:ρ为流体密度,kg/m3;ρw,ρa分别为水、空气的密度, kg/m3;μ为流体动力黏性系数,Pa·s;μw,μa分别为水、空气的黏性系数,Pa·s;C为液相的体积分数,1-C为气相的体积分数,当0 冲击式水轮机内部流动基本控制方程为 (3) (4) 式中:u为流体速度,m/s;x为坐标,m;t为时间,s;p为压力,Pa;ν为流体运动黏性系数,m2/s;f为质量力,m/s2;下标i,j为张量坐标,m. 研究采用具有良好近壁面特性的SSTk-ω湍流模型对冲击式水轮机内部流动进行数值模拟.该湍流模型的湍动能k方程及耗散率ω方程如下,即 (5) (6) 上述式中:Gk为湍动能k产生项;Gω为ω产生项;Yk和Yω分别为k和ω的有效扩散项;Sk和Sω为用户自定义源项;Dω为正交发散项;μt为湍涡流动力黏性系数, m2/s,σk和σω分别为k和ω的湍流普朗特数;F1为壁面函数值. (7) (8) (9) 根据吉牛水电站冲击式水轮机设计资料,以及水电站给出的水轮机喷嘴射流中心线与转轮斗叶节圆直径偏移量S(5.78 mm),建立水轮机过流部件水体模型.按国家标准[15]允许的最大偏移值,分别向转轮斗叶外缘和中心方向偏移,射流偏移如图1所示;水轮机基本设计参数见表1,所建水体模型如图2所示. 表1 吉牛水电站水轮机基本参数 图1 射流偏移示意图 图2 三维水体模型 吉牛水电站冲击式水轮机主要过流部件由6个喷嘴和喷针及1套21叶片的转轮组成,每个喷嘴在轴向上安装了2组导流板,以约束喷嘴内部水体流动过程中的能量交换. 采用非结构的Poly-Hexcore复合型网格进行几何模型计算域网格划分,以效率为目标对其进行网格无关性验证.验证结果见表2,表中N为网格数;ηc,ηr,RE分别为计算效率、额定效率、相对误差.最终选定方案3为数值计算网格模型,该方案喷嘴内流道域、空气域及静止域的网格数为698万个,旋转域的网格数为514万个.基于研究重点区域为喷针和水斗表面,方案3网格模型在重点研究区域的y+值为10~100,基本符合SSTk-ω湍流模型对网格质量的要求.几何模型局部网格划分如图3所示. 表2 网格无关性验证 图3 几何模型局部网格划分 依据吉牛水电站冲击式水轮机额定工况时的流动条件进行边界条件设置.进口边界条件设为速度进口vin(7.51 m/s),出口边界条件设为压力出口(guage pressure)0.设置旋转域交界面,转轮采用moving wall设置.采用transient rotor stator模型实现旋转域与静止域之间的信息传递.近壁区采用标准壁面函数. 分别对计算步长0.5°,1.0°和2.0°为1步进行计算后发现,0.5°和1.0°为1步的计算结果无差异;同时为了节约计算资源,采用1.0°为1步的计算设置,计算时间步长设置为0.000 556 s,时间步为3 600步,计算周期为10转. 采用VOF多相流模型和SSTk-ω湍流模型[16],对吉牛水电站冲击式水轮机在额定工况时,分别对3种偏移运行工况进行数值计算:PY+(喷嘴射流中心线向转轮斗叶外缘方向偏移5.78 mm)、PY-(喷嘴射流中心线向中心方向偏移5.78 mm)、PY0(无偏移). 为了验证不同湍流模型对冲击式水轮机的影响,对Standardk-ε,RNGk-ε,SSTk-ω3种湍流模型均进行运行效率数值模拟.模拟结果见表3. 表3 不同湍流模型的比较 综合对表3的分析,湍流模型采用SSTk-ω模型相对误差最小,同时验证了数值模拟的准确性. 转轮受力不平衡会引起质量偏心,产生不平衡离心力,引起转子弓状回旋和支承横向振动,增加轴承磨损,降低机械效率,甚至引发破坏性事故.研究中监测了转轮在运行过程中轴向z、径向r和切向τ的受力F,并取计算收敛稳定后的0.80~1.00 s为1个旋转周期的数据进行了分析.在3种运行工况下,转轮的径向力、轴向力和切向力均表现为不规则的震荡趋势,如图4所示,图中t为时间. 图4 转轮3种运行工况下z,r,τ向受力随时间变化曲线 表4为转轮3种运行工况下z,r,τ方向受力最大值Fmax、水导振摆值R和水轮机运行效率实测值ηt.根据表4和图4可知,偏移后,转轮轴向z的最大受力增加很大,工况PY+增大了2.27倍,PY-增大了1.79倍;实测斗叶向外缘方向偏移后,轴向振动值高达3.40倍,径向摆度也达到了1.30倍.表明对水轮机轴向振动影响很大,也增大了抬机的风险,这在水轮机振摆实测数据中也得到了充分体现,但都还未达到预警值. 表4 转轮3种运行工况下z,r,τ方向的受力及振摆和效率实测值 转轮径向r的最大受力有所减小,工况PY-的径向力减小了30.22%,PY+减小了12.58%,如果不考虑压力脉动,单从受力考虑,发生径向偏移后径向摆动值有所减小;尽管切向τ的受力减小得很少,仅0.19%,但由于切向力与转轮转矩有关,并直接影响出力和效率,因此减少了水轮机的出力和效率.计算表明效率减小了0.33%. 为了观测水轮机转轮内部压力脉动情况,在斗叶工作面及分水刃按每100 mm为间隔,等距离设置了11个监测点:GZM1—GZM7,FSR1—FSR4;为了观测分水刃背面水流干涉现象对压力脉动的影响,在斗叶背面从尖端到根部位置等距设置了3个监测点:BM1—BM3,如图5所示. 图5 转轮斗叶压力脉动监测点布置 流体在管道内流动时,其惯性力和管道的阻力共同作用产生不同大小的压力脉动.定义压力脉动系数Cp与压力脉动相对幅值ΔH/H这2个量纲一的参数作为量化冲击式水轮机压力脉动强度的参数.表达式为 (10) (11) 式中:ΔH为水头压力脉动峰峰值;H为水头;pumax,pumin分别为u点处压力最大和最小值;Cp为量纲一的压力脉动系数;pu为u点相对应的压力;参考压力pref为1.01×105Pa. 为了分析不同监测点在3种运行工况下的压力脉动系数情况,取计算时长为0.8~1.0 s一个旋转周期的数据进行分析.斗叶在1个旋转周期中平均压力脉动系数Cp,a的变化及压力脉动相对幅值见表5;1个旋转周期内,斗叶内各监测点的压力脉动相对幅值周向分布情况如图6所示. 表5 3种运行工况斗叶监测点平均压力脉动系数和压力脉动相对幅值 图6 3种运行工况各监测点压力脉动相对幅值周向分布 图7为3种运行情况分水刃监测点压力脉动系数.在分水刃上,从分水刃尖端到水斗根部方向,径向偏移对压力脉动的影响呈逐渐增大的趋势.越靠近水斗根部,径向偏移后的压力波动越大于无偏移工况,见表4以及图6a和图7所示.这样,在运行过程中,发生径向偏移后,靠近水斗根部的位置更容易发生破坏. 图7 3种运行工况分水刃监测点压力脉动系数 图8为3种运行情况工作面监测点压力脉动系数.在斗叶工作面上,靠近分水刃尖端与水斗根部位置,径向偏移对压力脉动的影响较大,其压力脉动相对幅值均大于无偏移运行工况,同时,工况PY+的压力脉动相对幅值较PY-更大.越靠近斗叶边缘(出水边监测点GZM7)处,偏移后的压力脉动相对幅值越大于无偏移情况,且径向偏移工况PY+的压力脉动相对幅值普遍大于PY-,见表4以及图6b和图8所示.这表明运行工况PY+对压力脉动影响大于PY-,并远远大于无偏移运行工况. 图8 3种运行情况工作面监测点压力脉动系数 图9为3种运行工况水斗背面监测点压力脉动系数.在斗叶背面,径向偏移运行工况的压力脉动相对幅值和系数的绝对值总体较小,从外缘到根部逐渐减小,偏移工况的压力脉动与无偏移工况相差不大,见表4以及图6c和图9所示.这表明偏移对背面的稳定性影响很小.压力脉动系数值多为负值,是由于水斗背面有凹面区域,射流的流动与斗叶背面之间容易形成空腔区域,产生负压.在监测点BM1处出现正压是因为部分水流冲击到分水刃尖端缺口的同时也冲击到了监测点BM1的区域,从而造成正压的产生. 图9 3种运行情况水斗背面监测点压力脉动系数 结果还表明,3种运行情况下工作面与分水刃处各监测点的压力脉动系数多为正值,仅背面的压力脉动系数多为负值,并且除了GZM7等个别监测点,其他监测点在3种运行工况的压力脉动系数差别不超过30%,但压力脉动相对幅值差异显著,尤其是工况PY+的明显增大. 在斗叶工作面,分水刃以及背面的压力脉动相对幅值变化具有一定的规律性.径向偏移后的压力脉动相对幅值较无偏移工况均呈现增大趋势,工况PY+较PY-增大更多,有的监测点是无偏移工况的3.28倍.监测点GZM1,GZM7及FSR2的压力脉动相对幅值在偏移前后的变化最明显,尤其是工况PY+的压力脉动相对幅值分别为PY0的1.82,3.28及2.60倍.最大相对幅值出现在工况PY+的FSR3,达到了29.95%. 对射流发生径向偏移后的冲击式水轮机稳定性进行了研究,得到以下主要结果: 1) 射流发生径向偏移后,转轮轴向受力远远大于无偏移工况的受力,吉牛水电站水轮机在国家标准规定的最大偏移量工况下,机组运行时轴向最大受力增大了2.27倍,实测斗叶向外缘方向偏移后轴向振动高达3.40倍,表明射流发生径向偏移会增大转轮轴向振动,加剧机组损害风险. 2) 射流发生径向偏移后,从分水刃尖端到水斗根部方向,对压力脉动的影响呈现逐渐增大的趋势,越靠近水斗根部,压力脉动相对幅值越大,斗叶工作面越靠近斗叶边缘出水边压力脉动相对幅值越大,向斗叶外缘方向偏移的压力脉动相对幅值均大于向中心方向偏移的,更远远大于无偏移工况的.吉牛水电站水轮机在国家标准规定的最大偏移量工况下,斗叶向外缘方向偏移工况较无偏移工况最大相对幅值达到3.28倍,实测斗叶向外缘方向偏移后径向摆度也达到了1.30倍. 3) 射流径向偏移转轮斗叶后,将引起水轮机轴向力和压力脉动显著增大,效率也有所降低,吉牛水电站水轮机在国家标准规定的最大偏移量工况下,实测效率降低了0.33%,尤其是射流向斗叶外缘方向偏移时,造成机组运行稳定性降低,安全风险增大.因此在冲击式水轮机机组安装以及运行过程中,应尽力避免发生射流径向偏移转轮斗叶情况.

2 几何模型及边界条件
2.1 过流部件三维水体模型建立


2.2 计算网格划分及无关性验证


2.3 边界条件设置
3 水轮机稳定性计算及结果分析
3.1 数值模拟结果验证

3.2 偏移对转轮受力的影响

3.3 偏移对转轮压力脉动的影响

4 结 论
