导电滑环的随机振动仿真分析研究
2023-12-26宗晓明张亚楠杨尚矗宋玉杰李宁
宗晓明,张亚楠,杨尚矗,宋玉杰,李宁
(中航光电科技股份有限公司,河南 洛阳 471003)
1 引言
导电滑环属于电接触滑动连接应用范畴,也被称为集电环,此外,还有旋转关节、集流环、汇流环等多种称法[1]。导电滑环可以实现两个相对转动体之间图像、数据信号及动力的传递。尤其适用于连续旋转、并需要把功率或数据从固定位置传送到旋转位置的场所,广泛应用于机械、电子、航空航天等领域[2-4]。
随机振动指那些无法用确定性函数描述,但又有一定统计规律的振动[5]。例如,车辆行进中的颠簸,阵风作用下结构的响应,喷气噪声引起的舱壁颤动及海上钻井平台发生的振动等。在导电滑环领域,随机振试验是环境试验的重要组成部分[6,7]。目前,对于导电滑环的随机振动性能考核多通过试验进行实测[8],尚未开展相关仿真技术的研究。近年来,用户对前端设计支撑的要求不断提升[9],需要在设计阶段对产品的随机振动工况进行模型建立与仿真分析。
本研究以导电滑环为研究对象,对导电滑环的刷丝组件、刷束组件和旋转轴系进行模型建立与随机振动工况的仿真分析,得到了三个方向上的形变和应力分布,为导电滑环仿真技术的发展提供理论基础和技术支持。
2 分析过程与方法
本研究以DX50 导电滑环为分析对象,导电滑环的结构图如图1 所示,该导电滑环共有12 路功率环和24路信号环,信号环采用刷丝结构,功率环采用刷束结构。刷丝组件与刷束组件的结构图如图2 所示。建模采用creo 软件,在进行随机振动仿真分析前需要求出分析结构的模态,首先使用仿真分析软件中的modal 模块进行模态分析求解,获得固有频率及振型。随后,在Random Vibration 模块开展随机振动分析。
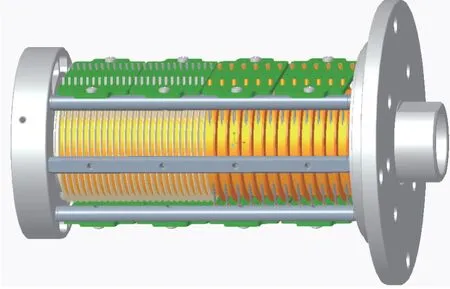
图1 DX50 导电滑环结构图
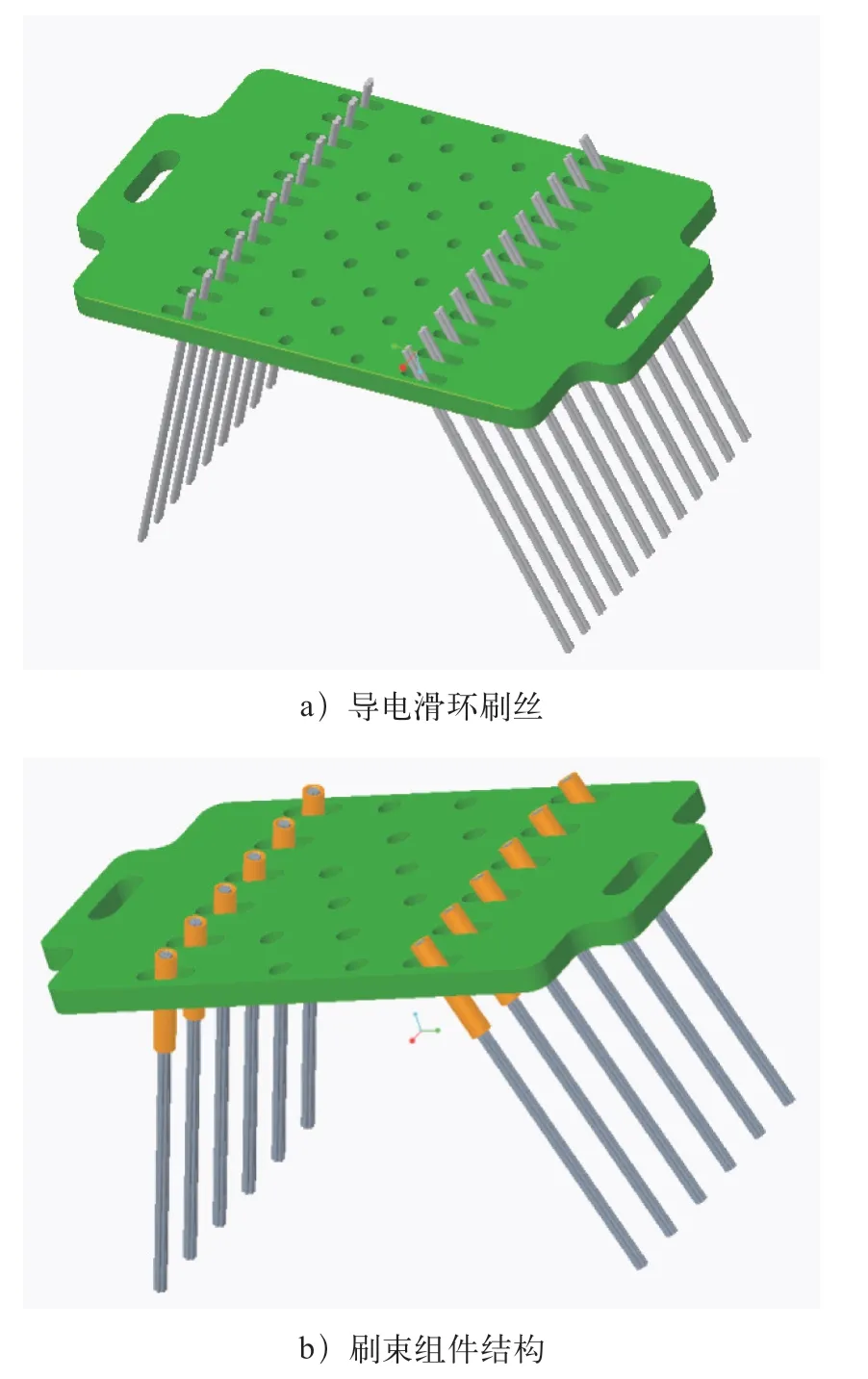
图2 导电滑环刷丝、刷束组件结构图
一般对于随机振动问题,用户会根据工况给出功率谱密度函数,后续分析都是基于给定的功率谱密度函数开展,对于复杂的工况,会给出多组不同的功率谱密度函数,以下以常见工况为例,对功率谱密度函数进行分析。某随机振动试验条件见表1。

表1 随机振动工况表
画出其功率谱密度曲线,如图3 所示,是由平直谱和斜线谱组合的简单谱。
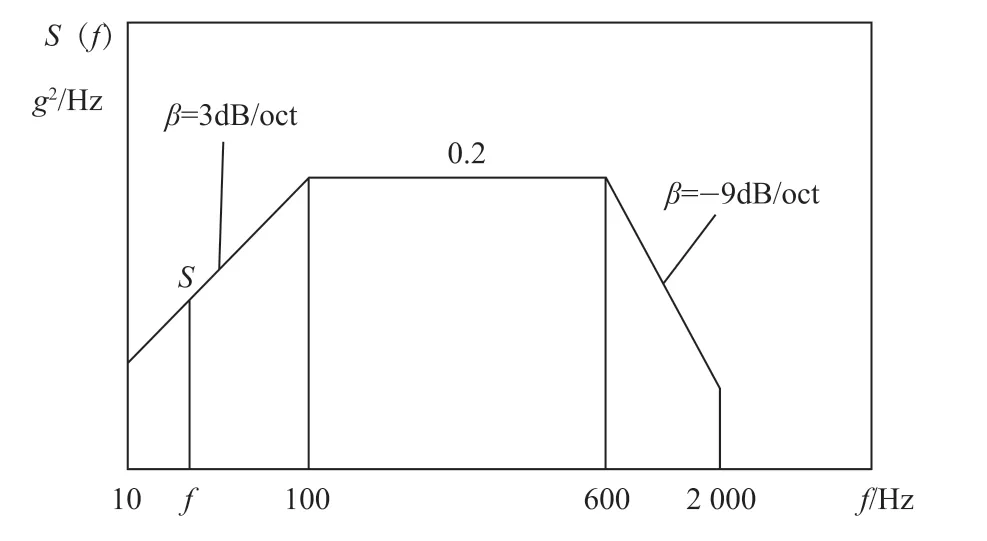
图3 随机振动的激励谱
图3 中,频率在100~ 600 Hz 范围内,功率谱密度函数为一个常数,这种随机过程称为“白噪声”随机过程,表示在该频带内,系统的输入加速度均方值是恒定的,为0.2g2/Hz。“非白噪声谱”的区域是用倍频程带宽增加或减少的分贝数表示的,因此需要转换为功率谱密度函数值,才能供计算分析使用。设斜线段的功率谱密度函数为S,频率为f,f0=100 Hz,S0=0.2g2/Hz,β为斜线段的斜率,则其转换公式推导如下:
由以上两个公式,即可求得10 Hz 和2 000 Hz 对应的功率谱密度分别为0.02 和0.005 4。
2.2 DXC50 旋转连接器随机振动工况分析
对于电旋转连接器产品,一般用户会给出随机振动的输入条件,典型的输入条件见表2,振动方向与电旋转连接器的对应安装位置如图4 所示。

表2 随机振动的试验条件
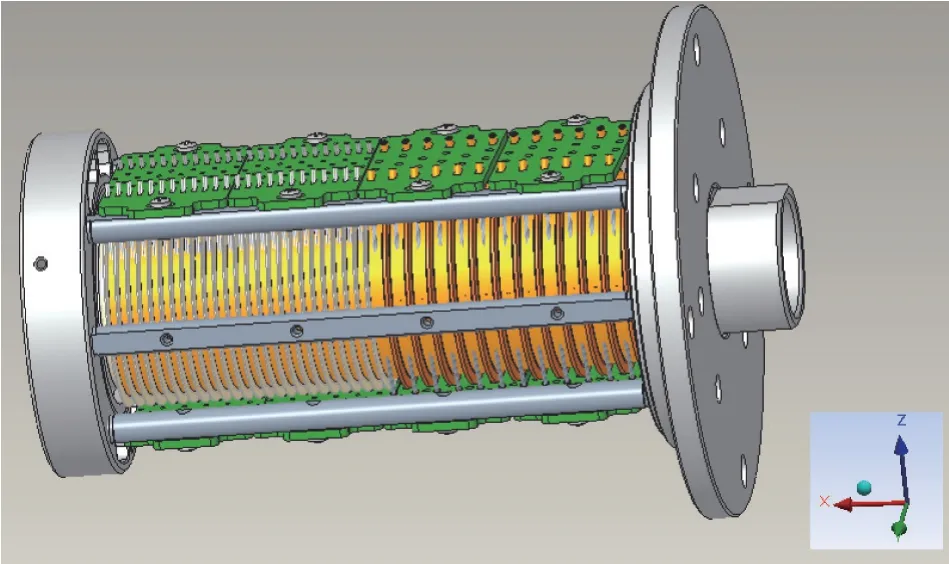
图4 振动方向与旋转连接器对应的安装位置
根据前述计算方法,即可求得10Hz 和2 000Hz 时功率谱密度分别为0.000 432g²/Hz 和0.000 216g²/Hz。其功率谱密度函数如图5 所示。
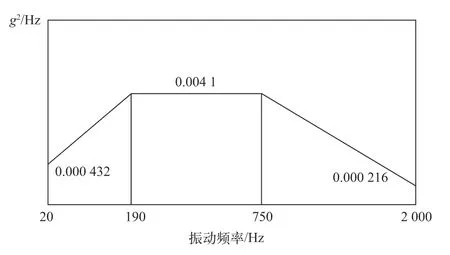
图5沿X、Y 和Z 方向的功率谱密度函数
3 结果与讨论
3.1 刷丝组件随机振动工况分析
刷丝组件的网格模型及固定位置如图6 所示,在分析时,将其左右两侧螺钉安装部位设置为固定端。在X、Y、Z方向上,分别施加随机振动工况。
X方向随机振动工况下的变形情况如图7 所示,可知最大变形量为6.49×10-4mm,发生在刷丝的边缘位置;X方向随机振动工况下的最大应力分布如图8 所示,可知最大应力为1.01MPa。
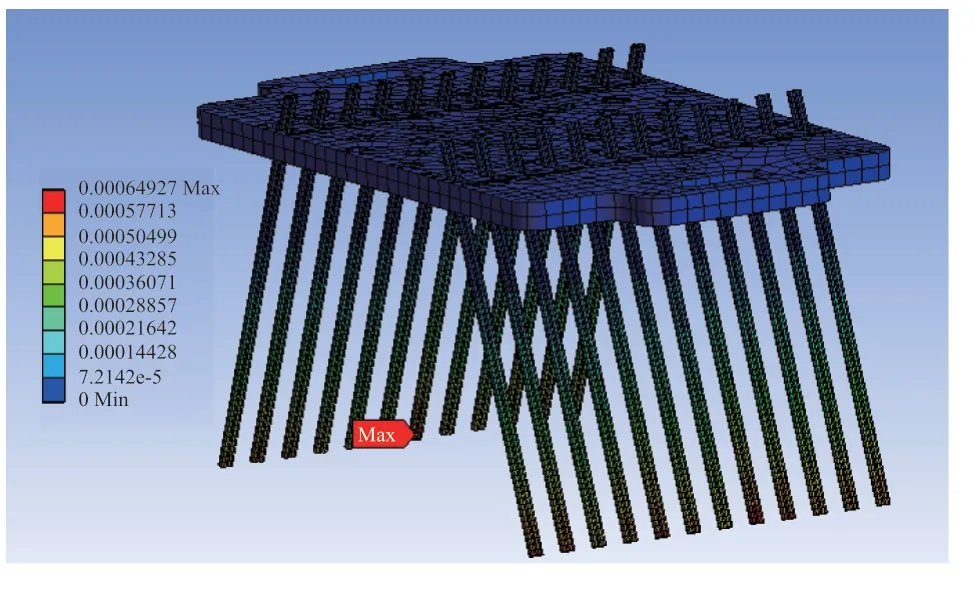
图7 X 方向上的随机振动位移情况

图8 X 方向上的随机振动应力情况
Y方向随机振动工况下的变形情况如图9 所示,可知最大变形量为1.07×10-5mm,发生在刷丝的边缘位置;Y方向随机振动工况下的最大应力分布如图10 所示,可知最大应力为0.017MPa。

图9 Y 方向上的随机振动位移情况

图10 Y 方向上的正弦振动应力情况
Z方向随机振动工况下的变形情况如图11 所示,可知最大变形量为2.44×10-3mm;Z方向随机振动工况下的最大应力分布如图12 所示,可知最大应力为3.82MPa。

图11 Z 方向上的随机振动位移情况
3.2 刷束组件随机振动工况分析
刷束组件的网格模型及固定情况如图13 所示,由于刷束模型较刷丝复杂,采用全尺寸仿真时模型过大,无法计算,因此对其进行了简化处理,仅留下一对刷束进行仿真计算。
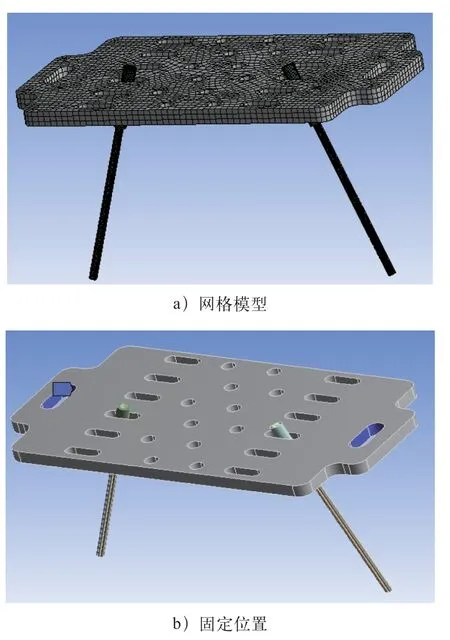
图13 刷束模型的网格模型及固定位置
X方向随机振动工况下的变形情况如图14 所示,可知最大变形量为1.18×10-5mm,发生在刷丝的边缘位置;X方向随机振动工况下的最大应力分布如图15 所示,可知最大应力为0.093 MPa。
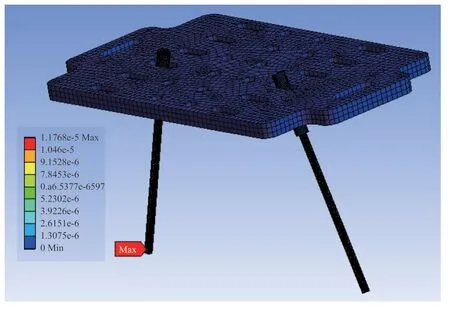
图14 X 方向上的随机振动位移情况
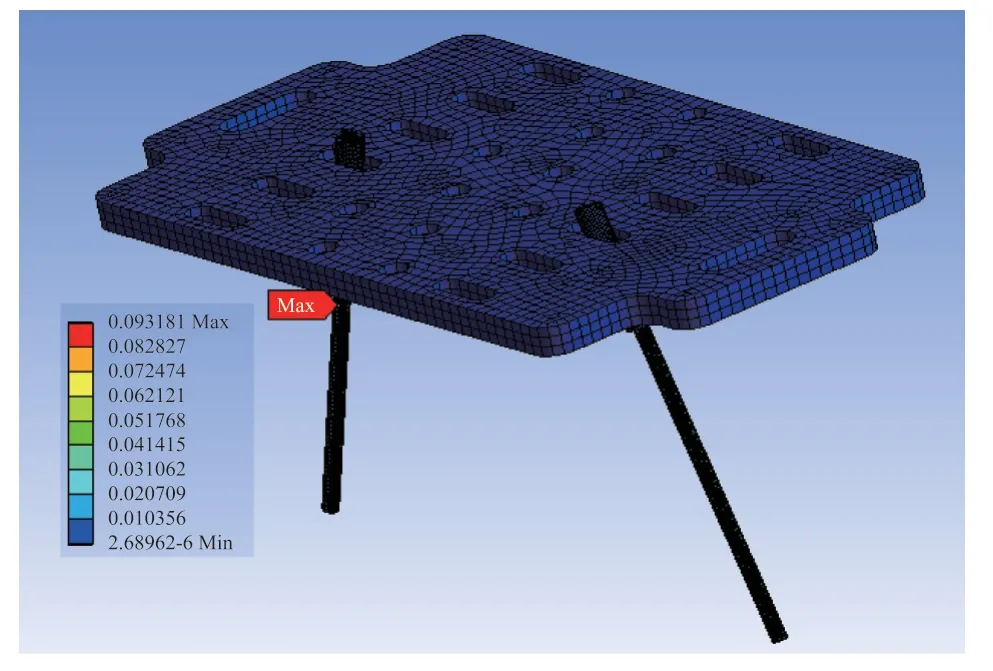
图15 X 方向上的随机振动应力情况
Y方向随机振动工况下的变形情况如图16 所示,可知最大变形量为4.29×10-7mm,发生在刷丝的边缘位置。
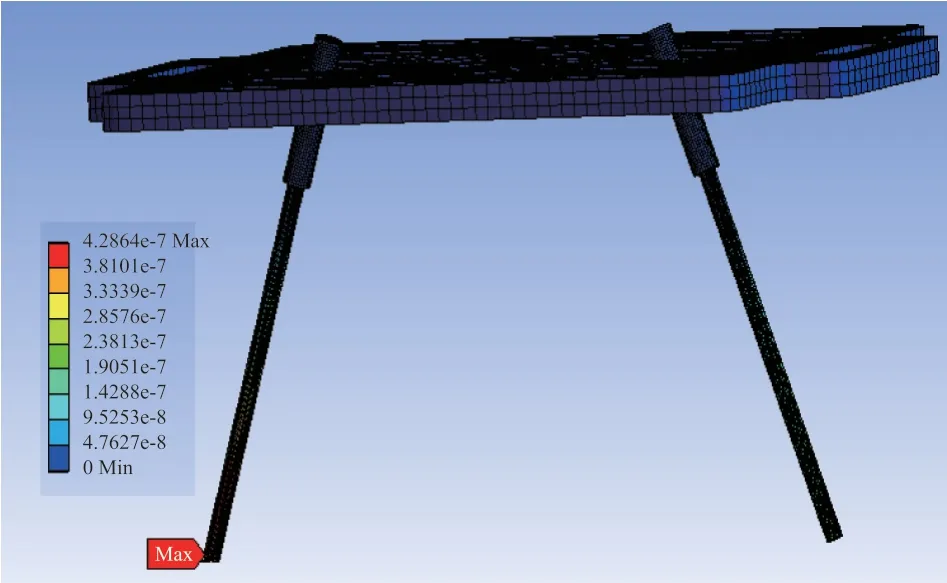
图16 Y 方向上的随机振动位移情况
Y方向随机振动工况下的最大应力分布如图17所示,可知最大应力为0.132 Ma。
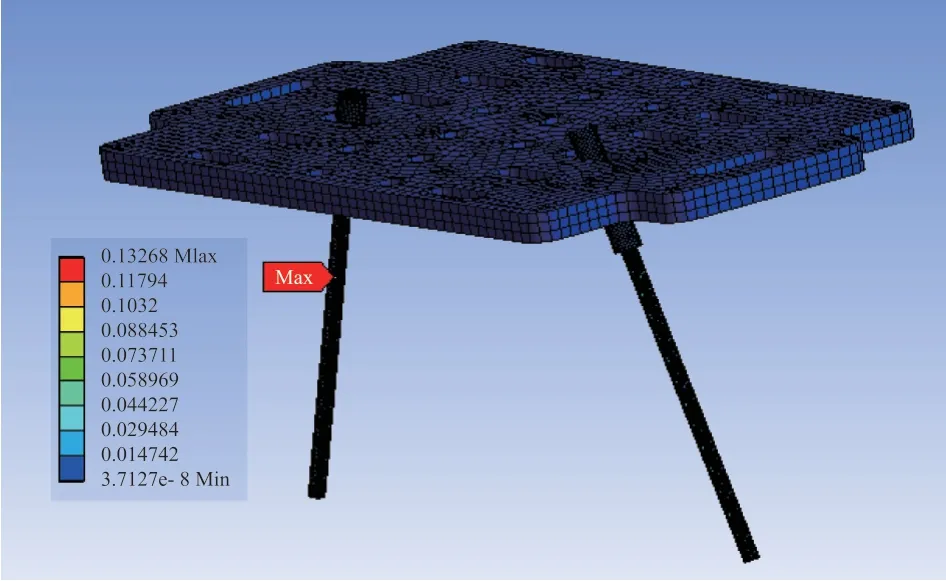
图17 Y 方向上的随机振动应力情况
Z方向随机振动工况下的变形情况如图18 所示,可知最大变形量为9.36×10-7mm,发生在刷丝的边缘位置;Z方向随机振动工况下的最大应力分布如图19 所示,可知最大应力为0.155 MPa。
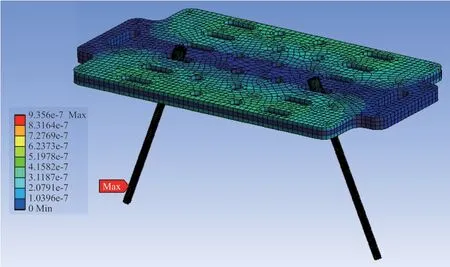
图18 Z 方向上的随机振动位移情况
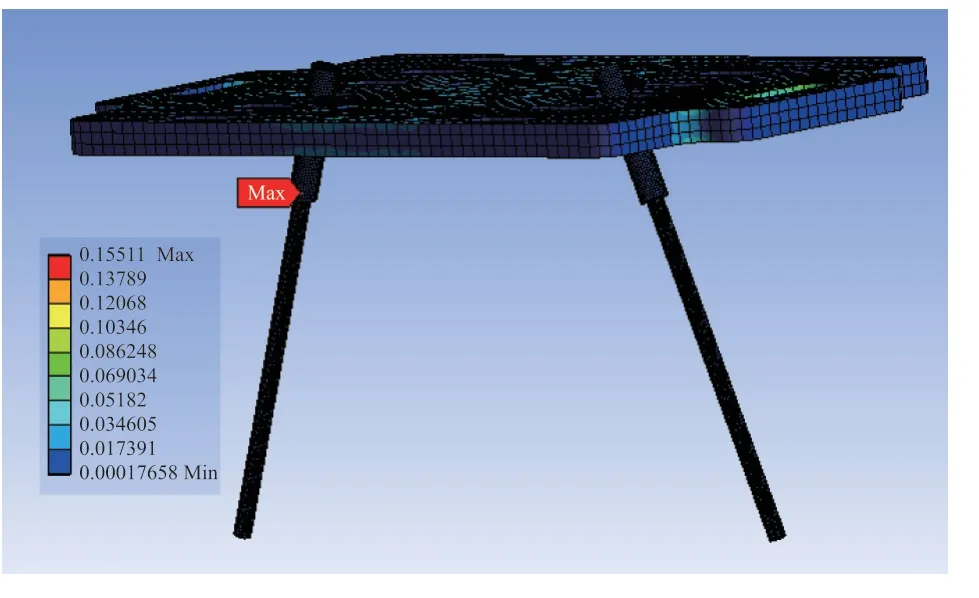
图19 Z 方向上的随机振动应力情况
3.3 旋转轴系随机振动工况分析
旋转轴系的网格模型及固定情况如图20 所示,由于旋转轴系模型相对复杂,对其进行了简化处理,仿真过程中保留轴系基础框架结构,并对倒角、微孔等细节进行了简化处理。

图20 旋转轴系的网格模型及固定情况
X方向正弦振动工况下的变形情况如图21 所示,可知最大变形量为1.13×10-7mm,发生在非固定端边缘位置;X方向正弦振动工况下的最大应力分布如图22 所示,可知最大应力为0.002 14 MPa,发生在轴承位置。
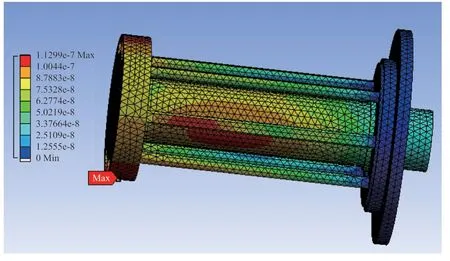
图21 X 方向上的随机振动位移情况
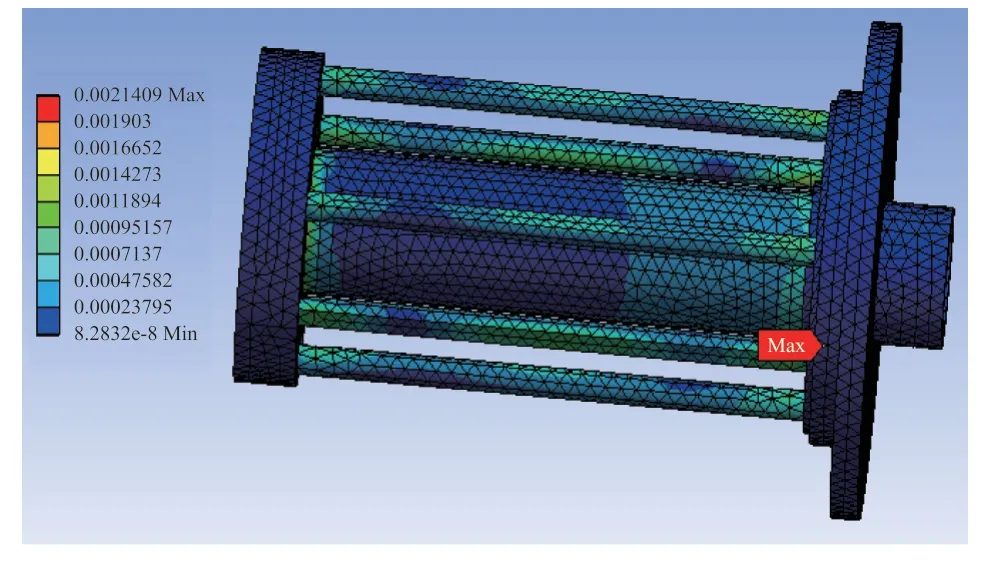
图22 X 方向上的随机振动应力情况
Y方向随机振动工况下的变形情况如图23 所示,可知最大变形量为2.92×10-4mm,发生在非固定端边缘位置;Y方向随机振动工况下的最大应力分布如图24 所示,可知最大应力为4.18 MPa,发生在轴承位置。
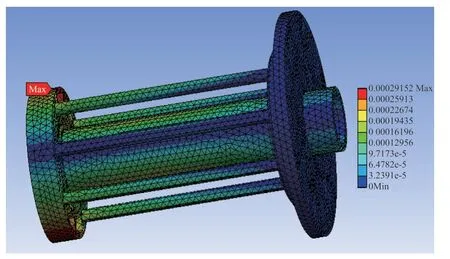
图23 Y 方向上的随机振动位移情况

图24 Y 方向上的随机振动应力情况
Z方向随机振动工况下的变形情况如图25 所示,可知最大变形量为1.89×10-4mm,发生在非固定端边缘位置;Z方向随机振动工况下的最大应力分布如图26 所示,可知最大应力为3.45MPa,发生在轴承位置。

图25 Z 方向上的随机振动位移情况

图26 Z 方向上的随机振动应力情况
4 结论
本论文对导电滑环随机振动工况进行了仿真分析,根据导电滑环的结构特点,分别对刷丝、刷架组件及旋转轴系的随机振动工况进行了仿真分析。得到以下结论:
1)对于刷丝组件,在给定随机振动工况条件下,最大应力为3.82 MPa,发生在刷丝与电路板连接位置,最大变形为2.44×10-3mm,发生在刷丝自由端。
2)对于刷束组件,在给定随机振动工况条件下,最大应力为0.155 MPa,发生在刷束与电路板连接位置,最大变形为1.18×10-5mm,发生在刷束自由端。
3)对于旋转轴系,在给定随机振动工况条件下,最大应力为4.18 MPa,最大变形为2.92×10-4mm,发生在非固定端边缘位置。
通过对导电滑环随机振动仿真分析研究可知,在给定工况下,刷丝组件、刷束组件和旋转轴系最大应力均处于较低水平,远小于金属材料的强度极限,整体结构安全可靠。通过本研究,增强了导电滑环产品设计的完整性,为导电滑环的基础研究提供了理论基础与技术支持。
