基于镜像蜜罐的USB病毒传播动力学研究

李汉伦, 任建国

(江苏师范大学 计算机科学与技术学院,江苏 徐州 221116)

0 引言

由于存储和交换数据的便利,U盘、移动硬盘等USB(universal serial bus)设备成为除网络外,传播计算机病毒的另一种主要载体.移动介质传播的USB病毒通过攻击计算机,达到数据泄露、机密窃取、文件篡改等非法目的[1-2].由于好奇心或缺乏安全意识等因素,人们有时会使用来路不明的移动介质[3],这增加了个人计算机和学校、企业等公用场所中计算机之间的交叉感染风险,使得病毒传播的速度更快、范围更广[4].

目前,研究人员通过建立数学模型研究移动介质对病毒传播行为的影响,如文献[5]为了研究良性蠕虫对恶意蠕虫的抑制作用,在易感—感染—免疫(susceptible-infected-recovered,SIR)模型[6-8]的基础上,建立了考虑移动介质和良性蠕虫的病毒传播模型,并重点关注与移动介质相关的参数对蠕虫传播的影响;文献[9]建立了外部计算机和移动介质两者同时影响计算机病毒传播的模型,得出模型仅有一个病毒平衡点,且地方病始终存在的结论;文献[10]根据反病毒软件的更新状态,把未感染的计算机分为弱保护状态和强保护状态,并研究它在移动介质影响下的传播规律,最后总结出用户意识对抑制病毒的传播起到关键作用;文献[11]通过在易感—感染—损毁(susceptible-infected-damaged,SIP)模型中加入移动介质的2种状态,对Stuxnet病毒的传播进行研究,并通过参数的讨论提出控制策略;文献[12]的模型同时考虑了网络拓扑结构和移动介质,在复杂网络环境下建立了更接近实际的病毒传播模型,结论指出,移动介质对病毒的传播行为具有重要影响;文献[13-14]在考虑网络拓扑结构的同时,建立了利用蜜罐对抗计算机病毒的仓室模型.用移动介质作为媒介进行病毒传播的研究虽然取得了一定进展,但在模型适用范围的讨论上还存在一定不足:一是忽略USB病毒与一般网络病毒在传播方式上的不同[15];二是未考虑系统中不同类型的主机与移动介质接触频率不同,主机被感染的概率也是不同的;三是移动介质从感染状态到易感状态的转化过于简单,不能反映使用者主观行为、反病毒策略和硬件环境与它之间的关系.

针对上述研究不足,受文献[13-14]在模型中引入蜜罐节点对抗病毒的启发,结合文献[15]提出的镜像蜜罐技术,建立同时考虑镜像蜜罐和网络拓扑结构的病毒传播模型.镜像蜜罐解决了现有网络检测方法对USB病毒无效的问题,本文的模型把镜像蜜罐作为独立仓室,为研究抑制USB病毒传播提供了参考依据.

1 模型构建

模型的建立需要考虑移动存储介质病毒的传播方式、镜像蜜罐的反病毒原理、移动介质使用者的行为习惯和网络拓扑结构.先根据与移动介质接触频率的不同,将网络中的计算机节点分为个体节点和公用节点.个体节点通常是网络中的个人计算机,此类节点与移动介质的接触频率较小并且在统一管理和部署镜像蜜罐上存在一定困难,而公用节点多存在于学校的打印室、多媒体教室、图书馆和机房等公共场所,这类节点通常存在多个USB接口,与不同移动介质的接触频率远大于个体节点,并且易由技术人员进行集中管理.当公用节点被感染了USB病毒的移动介质感染后,镜像蜜罐随即捕获到病毒样本并将它保存在镜像文件中,同时将计算机中的病毒清除,防止进一步感染其他移动介质.镜像文件中存有病毒样本的公用节点称为捕获节点.与网络蜜罐类似,镜像蜜罐捕获到病毒样本后通过发布免疫信息使个体进入免疫状态[13].免疫信息的反馈需个体节点和公用节点之间进行直接的数据通信来完成,而节点之间的均匀接触不足以反映实际网络的通信情况,因此,利用平均场理论建立考虑度分布非均匀的USB病毒传播模型.

通过以上分析,对模型作以下关键假设:

1)由个体节点和公用节点组成的网络为非均匀网络,且节点之间的连接不具有度相关性,度分布服从幂指数为σ的幂律分布p(k)～k-σ,p(k)表示在网络中随机选取的节点度为k的概率.令Δ表示节点度的最大值,个体节点和公用节点的平均度为

易感或感染个体节点的一条边连接到捕获节点的概率为

2)个体节点均未部署镜像蜜罐,根据状态的不同,分为3类节点:易感节点、感染节点、免疫节点.

3)公用节点均部署了镜像蜜罐,根据状态的不同,分为2类节点:易感节点和捕获节点.

4)移动介质根据状态的不同分为2类节点:易感节点和感染节点.USB病毒仅通过移动介质在个体节点之间传播,传播模式为“移动介质—计算机—移动介质”.

5)公用节点被移动介质感染后,镜像蜜罐必定能捕获到病毒样本,且捕获后镜像蜜罐立即清除病毒,避免进一步感染其他移动介质.

模型中变量和参数的定义如表1所示.

节点、移动介质的状态(用节点、移动介质的密度表示,下同)转化关系如下:

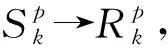
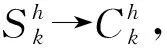
Sm→Im,易感移动介质与感染个体节点接触,被病毒感染.

Im→Sm,感染移动介质与公用节点接触,病毒被镜像蜜罐识别,采取某种杀毒措施将移动介质中的病毒清除.由于移动介质不具有免疫能力,因此,病毒被清除后仍处于易感状态.

模型各个状态之间的转化示意图见图1.

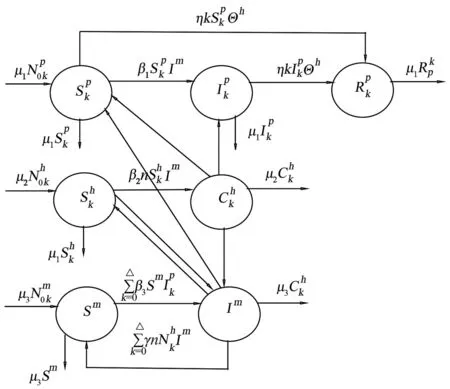
图中的圆框表示节点所处的状态,箭头线表示节点状态的转化方向,箭头线上的符号表示状态转换参数.图1 模型的状态转化示意图Fig.1 State transition diagram of model

模型的微分动力学方程[13]如下:

(1)

1.1 模型动力学分析

Nm(t)=Sm(t)+Im(t),

对系统(1)进行化简,可以得到如下子系统:

(2)

系统(2)的可行域为

该集合为系统(2)的正不变集.

由平衡点存在的条件,得到系统(2)唯一的无病平衡点

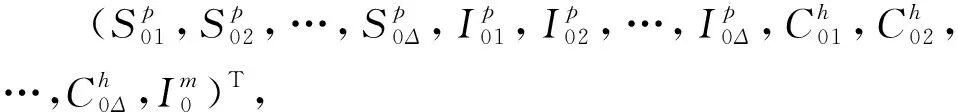
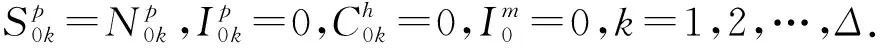
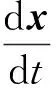
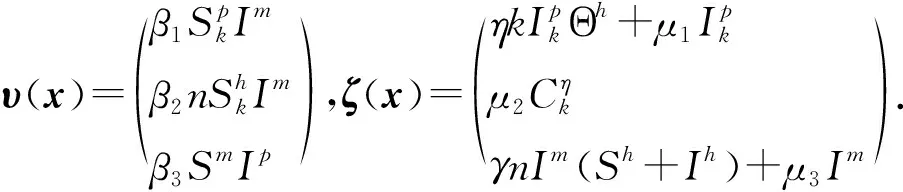
有

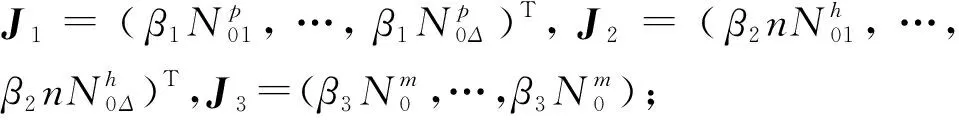
由此得到(2Δ+1)×(2Δ+1)阶的再生矩阵

通过计算FV-1的最大特征值,得到其谱半径ρ(FV-1)的数学表达式,因此,系统(2)的基本再生数

在流行病学中,基本再生数是决定病毒是否流行的传播阈值,本文所讨论的模型中,它表示单个的感染个体节点和感染移动介质在移出感染状态之前所能感染的易感个体节点和易感移动介质的数量.当R0<1时,被感染节点(包括系统(2)中被感染的个体节点、捕获节点和被感染的移动介质)的数量逐渐趋于0,即病毒最终会从计算机和移动介质中消失;当R0>1时,被感染节点的数量逐渐趋于正的常量,即病毒会始终存在于计算机和移动介质中.由于病毒不直接通过网络在计算机之间进行传播,病毒流行与否不受网络拓扑结构的直接影响,因此,在预测病毒的爆发和制定应对措施时应重点关注模型中2类感染率(从移动介质到计算机的感染率和从计算机到移动介质的感染率)和移动介质上的病毒清除率.除USB病毒本身的特性外,感染率β1还和移动介质使用者对陌生移动介质的使用率有关,β2则与移动介质使用者的使用范围有关.

1.2 平衡点的稳定性

定理1当R0<1时,系统(2)的无病平衡点E0在Ω上局部渐近稳定;R0>1时不稳定.

证系统(2)在无病平衡点E0处的Jacobian矩阵为

(3)

其中

L1=diag(-μ1,…,-μ1),

L2=diag(-μ2,…,-μ2),

矩阵(3)的特征多项式为

该式有2Δ重具有负实部的特征根-μ1,Δ重具有负实部的特征根-μ2和特征根

其中

2 仿真分析

为验证系统的理论分析结果和更好地观察病毒的传播规律,我们在Intel Core i3-10110U CPU、主频2.1 GHz、内存4 GB,Windows 10操作系统环境下,采用MATLAB R2020a平台进行仿真实验,并假定系统所有参数的取值为正的常量.实验重点关注个体节点和移动介质在各参数影响下的感染情况,其中涉及的参数取值情况见表2.

易知,在服从幂指数为2.4、网络最大度为20的幂律分布网络中,经计算,由个体节点和公用节点所组成的网络平均度为2.36.此外,为了便于观察网络拓扑结构对不同度值的个体节点密度随时间演变的影响,假设系统不同度值的公用节点和个体节点的初始值均相同.

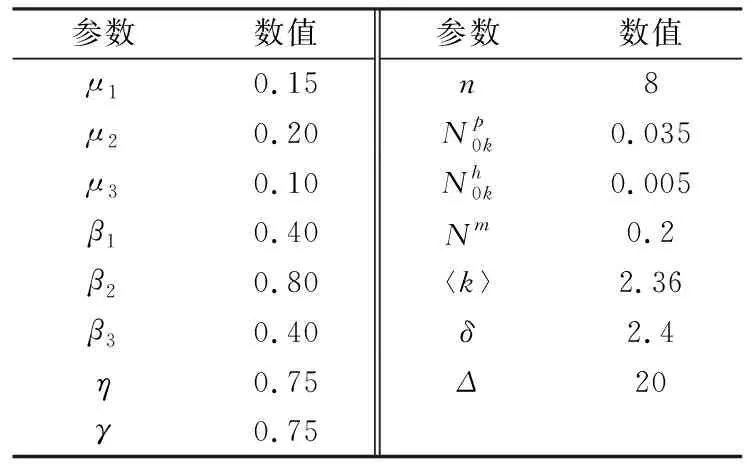
表2 实验的参数设置Tab.2 Setting of experimental parameters

首先,研究个体感染节点、捕获节点和感染移动介质的密度随时间的整体演变趋势.当系统各参数取表2所示的值时,传播阈值R0=0.57<1,因此,只要经过足够长的时间,病毒将从个体节点和移动介质中彻底消失,图2a验证了这一点.此外,由R0表达式知,病毒最终是否会消失不受移动介质更换率的影响.接着,取γ=0.01,其他参数同表2,此时R0=1.38>1,病毒将持续存在于个体节点和移动介质中,由图2b可以看出,在大幅降低移动介质上的病毒清除率后,感染个体节点和感染移动介质密度在短暂增加后仍出现大幅减少趋势,表明此状况下病毒虽然会一直存在于个体节点和移动介质中,但短时间内病毒的传播得到了较好的抑制.为进一步研究其他因素对病毒爆发的影响,在其他参数与表2一致的情况下,取γ=0.01、μ3=0.02,此时R0=5.33>1,由图2c可以看出,感染移动介质的密度在短暂的下降后又迅速提高并稳定在某个值上,原因是系统前期只有少量的感染个体节点,此时感染移动介质的减少速度大于被感染个体节点新感染的移动介质的增加速度,但随着感染个体节点密度的不断提高,被新感染的移动介质的增加速度超过了减少速度,因此感染移动介质的密度出现上升趋势.

为研究β1和β32类感染率对感染个体节点密度变化影响的异同,将β1和β3分别取一组相同的值,其他参数取值同表2.从图3可以看出,2类感染率在取值相同的情况下,感染个体节点的变化趋势是有差别的.图3a、b中不同感染率取值下的感染个体节点密度几乎均在t=4.57 h时达到峰值;不同的是,β1取不同数值时,感染个体节点的密度几乎在同一时刻达到不同的峰值(图3a),而β3取不同数值时,感染个体节点密度几乎在同一时刻达到非常接近的峰值(图3b).

图3 2类感染率下感染节点密度随时间的演变Fig.3 Evolution of infection node density with time under two different infection rates

图4中,μ3=0.02,其他参数取值同表2.图像显示了在移动介质的更换率和病毒清除率同时取相对较小值的情况下,通过提高病毒清除率后的感染个体节点和感染移动介质密度变化曲线.t相同时,Ip(t)、Cn(t)越大,对应的γ越小,即越是上面的曲线对应的γ取值越小.因此,通过提高移动介质的病毒清除率,病毒在移动介质中的传播得到了明显的抑制,同时间接减少了个体节点的感染规模,即通过技术手段提高移动介质的病毒清除率以及提高使用者对移动介质的杀毒意识可以充分发挥镜像蜜罐的作用,从而对病毒的传播起到更好的控制效果[17].图5中,μ3=0.02、γ=0.01,其他参数取值同表2.图像显示了不同的反馈率对病毒抑制的效果,越是居上的曲线对应的η值越大.与图4相同之处在于通过提高反馈率同样可以减少感染的个体节点和移动介质,不同的是,与图4b相比,在不同反馈率的作用下,图5的感染移动介质密度几乎以相同的速度下降到极为接近的最小值,然后才以不同的速度迅速递增,因此,在相同条件下,病毒清除率的提高对抑制病毒传播的效果更为明显.

图6中,γ=0.01、μ3=0.02,其他参数取值同表2.图像显示了网络拓扑结构对镜像蜜罐反馈免疫信息效用的影响,可以看出,图6a中越是上面的曲线对应的度值越小,图6b中越是上面的曲线对应的幂指数越大,因此,度大的个体节点比度小的更易接收到免疫信息,而网络的幂指数越小,被感染的个体节点就越少.由于反馈率η并不影响基本再生数的值,而节点度值和幂指数的改变仅能影响免疫信息的反馈效果,因此,在该模型中病毒的传播行为受网络拓扑结构的影响较小.

图4 不同病毒清除率γ下感染节点密度随时间的演变Fig.4 Evolution of infected node densitiy with time under different virus clearance γ

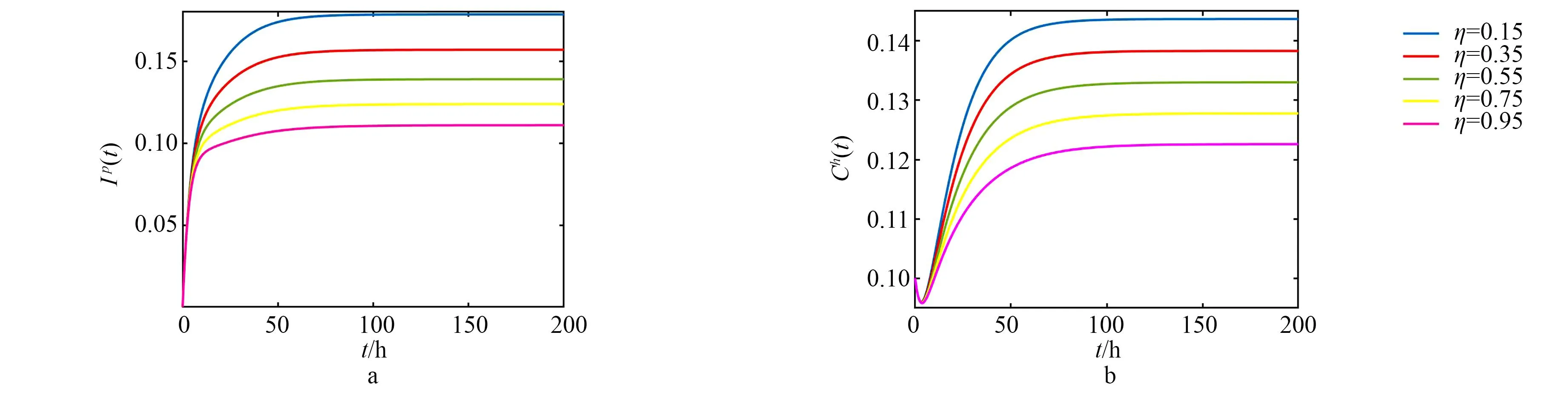
图5 不同反馈率η下感染节点密度随时间的演变Fig.5 Evolution of infected node density with time under different feedback rates η

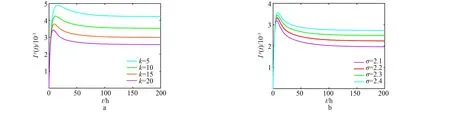
图6 网络拓扑结构对感染个体节点密度演变的影响Fig.6 Influence of network topology on evolution of infected individual node density

3 结论

由于缺乏统一和有效的管理及防御措施,目前对仅通过移动介质进行传播的USB病毒的相关研究较少,并缺少相应的数学模型和仿真实验可供参考.从移动介质使用者行为习惯角度出发,构建一类防御此类病毒的新颖模型,通过模型的动力学分析并对影响USB病毒传播行为的几个重要参数进行仿真,得到如下具有现实意义的结论:

1)当感染率一定时,移动介质的更换率和病毒清除率同时较低时,系统的感染情况最为严重,此时镜像蜜罐难以发挥作用.通过提高使用者清除病毒的主动性和科学性,避免感染了病毒的移动介质长期且大范围地在个体节点之间使用.

2)从移动介质到个体节点的感染率和从个体节点到移动介质的感染率对病毒传播行为的影响是不同的,感染个体节点的密度受前者的取值变化影响较大,通过限制或减少对陌生移动介质的使用可以减小其值.

3)USB病毒的传播行为受网络拓扑结构的影响较小,受USB病毒传播特性和移动介质使用者的主观行为影响较大.