基于LOGISTIC的海南热带雨林国家公园公路沿线地质灾害敏感性评价

李 信 ,薛桂澄 ,柳长柱 ,马 波，杨永鹏，杨 峰，王晓林

1.海南省海洋地质资源与环境重点实验室，海南海口 570206；2.海南省地质调查院，海南海口 570206

地质灾害敏感性是指一定空间范围内，在自然和人类活动作用下，发生地质灾害的可能性。山区公路沿线的地质灾害敏感性是指在山区公路沿线，当自然或人为因素导致某一地段或段落发生地质灾害的可能性。开展地质灾害敏感性评价与区划，可以有效地识别地质灾害敏感性，对地质灾害精准化监测与防控具有指导意义。海南热带雨林国家公园位于海南岛中部山区，是建设中的海南自由贸易港的重要组成部分，也是海南国家生态文明试验区的核心区，加强海南热带雨林国家公园的地质环境监测和保护具有重要意义。开展海南热带雨林国家公园山区公路沿线的地质灾害敏感性评价与区划，可以有针对性地为海南热带雨林国家公园管理局提供地质灾害防治措施和减灾建议，提高对山区公路沿线地质灾害的监测与预警能力。随着GIS的应用推广和机器学习理论日臻完善，地质灾害影响因素相关性定量化程度越来越高，地质灾害敏感性评价在机器学习和深度学习的加持下，敏感性评价预测的准确性得到了大幅度的提升。目前地质灾害敏感性因素的定量研究主要基于证据权重法（赵祈溶等，2021）、信息量法（彭珂等，2018；李信等，2022a；赖波等，2023；章昱等，2023）、频率比（齐信等，2017）、贡献率（吴森等,2016）、确定性系数（李剑锋等，2021）等热门方法；而基于敏感性指数与地质灾害影响是否呈线性关系，敏感性评价模型有模糊数学、多元回归分析、层次分析法的线性假设模型和灰色理论、人工神经网络、支持向量机等非线性假设模型（Althuwaynee et al.,2016；张晓敏等,2018；Adineh et al.,2018；宋亚娅和张航泊,2020；Nanehkaran et al.,2022；李明等，2023）；实际研究中敏感性因素对地质灾害发生并不是一致的线性关系，前者缺点是结果客观性不强，后者需要对样本数据进行深度挖掘才能得到较好的非线性假设，对于样本不大的区域适用性不高。确定性系数法评价地质灾害敏感性具有可操作性强和运用广泛等特点；作为一种机器学习方法，逻辑回归模型不需要曲线估计，只需对对数概率进行转换，将敏感性因子与地质灾害发生与否的非线性关系变换为线性关系，是一种较为成熟的统计方法（Ayalew and Yamagishi,2005）；李信等（2022b）以五指山市为例分别利用逻辑回归模型与信息量模型的耦合模型和信息量的单一模型进行敏感性评价，结果显示耦合模型预测的准确性更高。以往研究尺度集中在县域行政区，对山区公路沿线开展的敏感性评价研究较少，本文将以国家热带雨林山区公路沿线为研究对象，选取断裂、坡度、坡向、水系、公路、降雨量作为敏感性评价指标，对地质灾害主控因素进行分级分析，采用确定性系数法与逻辑回归的耦合模型和确定性系数的单一模型开展地质灾害敏感性评价；并对评价的准确性和合理性进行对比分析。研究成果将为海南热带雨林国家公园沿线公路地质灾害防治和灾害预警提供科学依据。

1 尖峰岭公园公路沿线地质概况

海南热带雨林国家公园尖峰岭园区位于海南岛西南部，乐东县的尖峰镇内（图1）。地理坐标为东经108°36′～109°05′，北纬18°23′～18°52′。尖峰岭园区地处热带北缘，属热带季风气候，年平均气温24.5°C，年平均降雨量2265.8 mm，年均相对湿度88%，年均日照时数1625 h。尖峰岭园区发育河流主要有东南向的南巴河和南向的望楼河，南巴河经昌化江汇流入海;望楼河经长茅水库后汇流入海。尖峰岭公园公路地区属侵蚀构造中低山区，最高的山峰为尖峰岭，海拔1400 m。

图1 海南省热带雨林公园概况图Fig.1 Overview of Hainan Tropical Rainforest Park

尖峰岭公园公路沿线地质环境条件较复杂，公路沿线面积约为96 km2；地层为第四系，岩性为砾质粘性土、冲洪积砂粒、粉砂；岩浆岩为二叠纪、三叠纪花岗岩。尖峰岭公园公路沿线发育的较大断裂为东西向尖峰-吊罗断裂带，小型断层为尖峰七队断层等。尖峰岭公园公路沿线崩塌地质灾害频发，共计80 处，发育密度最高为2.87 处/km2，严重威胁公路沿线过往的人民生命财产安全。

2 研究方法

地质灾害影响因素分析旨在通过概率函数将影响因子定量化，来衡量在不同因子条件下地质灾害的响应程度（罗路广等,2021a）。确定性系数模型是指将各因子分级区间内地质灾害个数转换成确定性系数，通过各级确定性系数大小变化规律判定因子分级内部的主控因素。以确定性系数为自变量，以是否发生地质灾害为因变量，运用二元逻辑回归模型，计算出二元回归系数，将回归系数归一化后作为刻画各个独立因子之间对地质灾害的影响程度大小，确定地质灾害影响因素在地质灾害敏感性评价中的权重，最后对定量化的图层进行叠加分析，形成地质灾害敏感性区划和结果。

2.1 确定性系数模型（CF）

确定性系数模型是精度较高、可操作性强且能定量地反映出地质灾害发育规律的模型（李剑锋等,2021）。该模型是假设已发生的地质灾害和未来将发生的灾害处于相同的地质环境条件下。计算公式为：

式中：ICF为确定性系数；Pa为地质灾害在因子a 中发生的条件概率，以因子a 中的地质灾害个数（或面积）与a的面积比值表示；Ps表示灾害总数（或面积）与总面积的比值。由公式（1）可知，ICF的变化范围为[-1，1]。ICF为正值时表示地质灾害发生的确定性高；ICF为负值时表示地质灾害发生的确定性低（李剑锋等,2021）。

2.2 确定性系数-逻辑回归模型（CFLR）

二元逻辑回归是一种能针对定性不连续变量进行有效、准确定量的预测统计模型（罗路广等,2021b）。该模型以确定性系数值为自变量（xi），以地质灾害发生与否（地质灾害发生取值为1，不发生为0）为因变量，建立逻辑回归方程预测地质灾害发生的概率（P）。二元逻辑回归模型操作简单，自变量类型可以是连续的也可以是离散的，在地质灾害易发性评价中得到广泛应用。逻辑回归函数公式为：

式中：P 为当Y 取值为1 时发生地质灾害的概率；xn为自变量，此处为确定性系数ICF；βn为逻辑回归系数。

利用确定性系数模型计算公式（1）计算出各个因子的敏感性指数ICF值，再将ICF值作为自变量代入逻辑回归模型公式（3）进行运算得出二元逻辑回归系数，最后将回归系数归一化为各评价因子的权重，并对所有评价因子加权求和得出确定性系数逻辑回归模型易发性指数ILRCF，公式如下：

3 影响因素敏感程度分析

由于众多影响因素中，不同因子之间存在一定的相关性，如坡度、起伏度等具有地质灾害发育响应的同方向性。Pourghasemi and Rossi（2017）回顾了2005～2012年220篇文献研究，坡度、地层岩性、坡向、土地利用、河流缓冲距离、海拔高程、断裂缓冲距离、平面曲率、剖面曲率、公路缓冲距离为从高到低使用频次前十的影响因子。根据前人研究成果和海南热带雨林国家公园地质背景，选取了地质灾害敏感性分析中最常使用的断裂、坡度、坡向、水系、公路、降雨量6个因素应用于本研究；利用确定性系数模型公式（1），运用GIS 空间分析功能绘制出敏感性分级与各因子之间的叠加分布图，基于各分级灾害百分比和面积百分比的敏感性指数的方法来衡量和刻画地质灾害在各因子分级内部的分布规律，因子分级间的数据采用右半开区间，即数据只含左端点而右端点不包含在内的区间（如图2）。

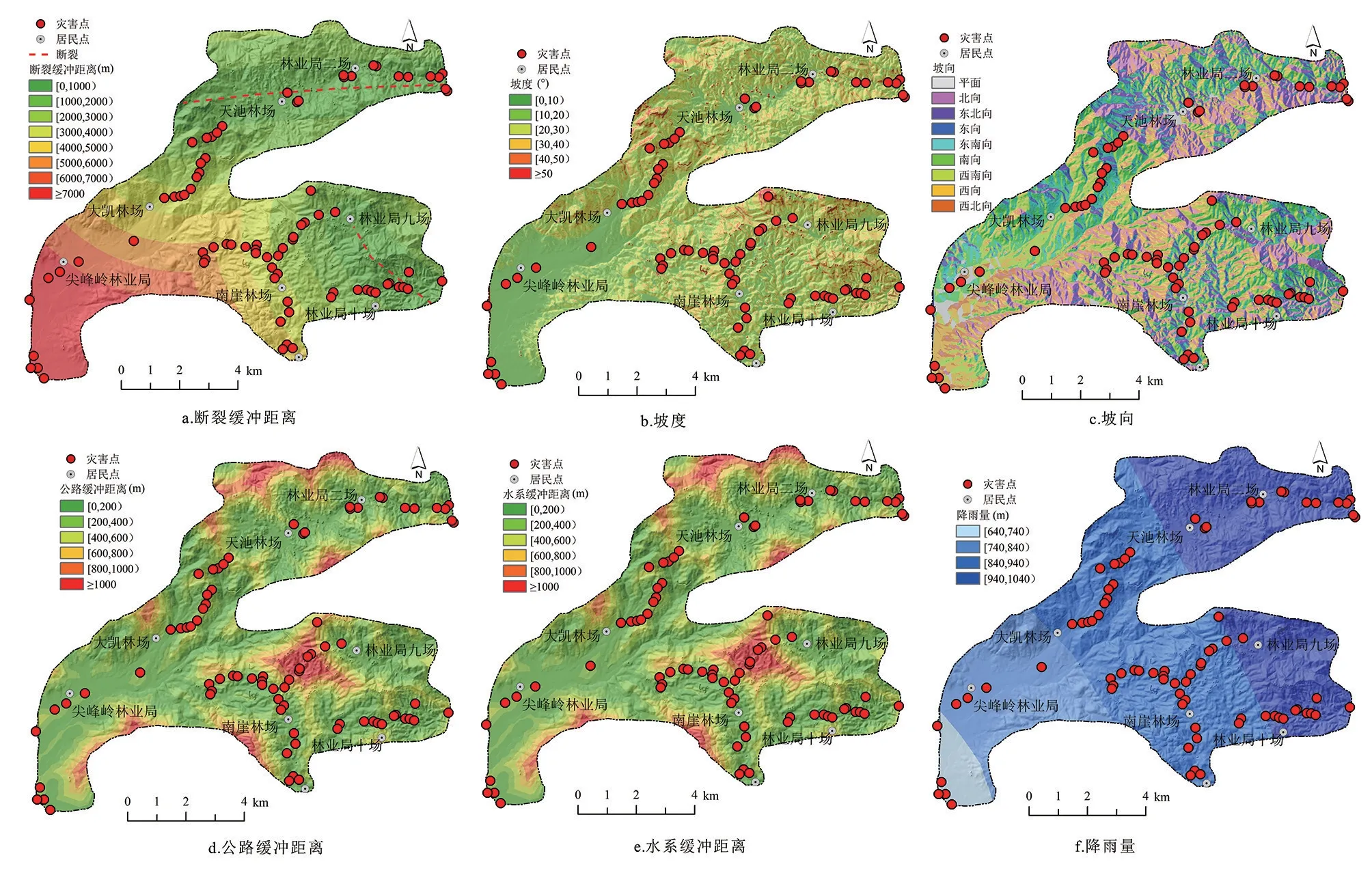
图2 研究区地质灾害影响因子分级图Fig.2 Classification map of susceptibility evaluation factors of geohazards in study area

3.1 断裂距离

断裂构造作用为灾害的孕育提供了破碎的岩层和软弱的结构面（刘广宁等,2019）。尖峰岭公园公路沿线主要的大断裂带为尖峰-吊罗构造断裂带，呈东西走向，位于北部的天池林场-林业局二厂一带；其次为尖峰七队断层，呈北西走向（图1）。断裂带一定范围内岩层破碎,裂隙、结构面发育，形成大量破碎、松散堆积物。黄润秋和李为乐（2009）就断裂构造对地质灾害影响范围进行研究表明：断裂在0～7000m范围内对地质灾害影响较大，故将尖峰岭公园公路沿线的断裂缓冲距离（单位：m）分级为[0,1000）、[1000,2000）、[2000,3000）、[3000,4000）、[4000,5000）、[5000,6000）、[6000,7000）、≥7000（图2a）。

断裂构造对崩塌、滑坡的发育延伸方向、发育规模及分布密度具有一定的控制作用（王高峰等,2017）。公路沿线地质灾害受东西向尖峰-吊罗构造（断裂）带以及尖峰七队断层的影响，如图3a所示距断裂带越近，地质灾害占比越大，距离断裂1000 m范围内地质灾害发育最多；随着距断裂缓冲距离的增加，地质灾害占比总体减少；在断裂缓冲距离（m）[3000，4000）处地质灾害百分比达到第二个高点，敏感性指数达到最大，为0.254，表明[3000 m，4000 m）是尖峰岭公路沿线地质灾害最易发生的断裂缓冲区间。由此可见，断裂是影响地质灾害发育分布的重要因素之一，断裂对地质灾害的影响作用随着距离的增加而减弱。

图3 研究区地质灾害影响因子分级敏感指数统计图Fig.3 Statistics of susceptibility evaluation index of geohazard in study area

3.2 坡度

坡度对斜坡体应力分布有直接影响，坡度的大小决定了坡体表层松散物失稳概率的大小（冯卫等,2021）。为便于分析，以10°坡度为间隔将尖峰岭公园公路沿线坡度（单位：°）划分为6级，分别为[0，10）、[10，20）、[20，30）、[30，40）、[40，50）、≥50（图3b）。尖峰岭公园公路沿线地质灾害主要分布在坡度以0～30°为主的地区（图2b）。敏感性分析结果表明，虽然在50°以上坡度范围内地质灾害分布不多，但是敏感性指数最高，表明此坡度段是崩塌地质灾害发育最有利的坡度。

地质体失稳破坏基本上发生于松散覆盖层与基岩交界面或岩石破碎的结构面，当坡度较低时，斜坡体上利于形成松散堆积物（张宏鑫等,2020）。如图3b，坡度在30°以内地质灾害占比最高，当坡度缓慢增长时，地质灾害敏感性指数呈现缓慢下降趋势；当坡度大于40°时，敏感性指数开始反转，其原因是道路工程的切坡、开挖诱发了大量的地质灾害；当坡度大于50°时，地质灾害发育数量不多，敏感性指数和频率比却达到峰值，主要是当坡度变陡时，斜坡上土体滑动力显著增大，超过摩擦阻力的临界值时，发生地质灾害的概率将显著增加。

3.3 坡向

太阳入射角度、辐射强度、辐射时间在不同坡向上存在一定的差异；植被发育状况和土壤湿度在不同的坡向上也存在较大的差异（冯凡等,2019）。本文将不同分布位置的坡向分为9 个，分别为平面、北坡、东北坡、东坡、东南坡、南坡、西南坡、西坡、西北坡（图2c）。通过坡向与地质灾害叠加分析，统计出地质灾害在各个方位上的分布，并计算各个坡向的敏感性指数。

向阳的南坡、东坡和东南坡是发生地质灾害的几率大于其他坡向。如图3c 所示，北坡、东坡、南坡、东南坡、西南坡方向的地质灾害发育占比超过了70%，主要因为受台风强降雨以及热带强辐射的影响，南坡、东坡方向向阳面的干湿循环速度明显高于阴面西坡的土体。

3.4 公路缓冲距离

公路施工常常伴随着斜坡体的开挖、切削，其对土体的振动、扰动改变了斜坡体的应力状态，降低了岩土体的粘聚力，增大了渗透系数，在强降雨的作用下形成地质灾害（张晓东等，2018；刘广宁等，2019）。尖峰岭公园公路包括西段的林业局场部至天池公路和东段的林业局场部至尖峰岭公路，根据公路切坡对地质灾害的影响情况，本文将公路缓冲距离（单位：m）划分为[0，200）、[200，400）、[400，600）、[600，800）、[800，1000）、≥1000六个区间（图2d）。对公路缓冲距离与地质灾害进行叠加分析，统计出地质灾害在不同缓冲距离区间内的分布，并计算其敏感性指数。

由图3d 可知，当公路缓冲距离在[0m，200m）区间时，敏感性指数最高，为0.297，其原因是公路施工切割坡体产生了众多的人工危岩或不稳定边坡，在强降雨作用下危岩或不稳定斜边坡易失稳发生崩塌、滑坡地质灾害。

3.5 水系缓冲距离

河流等地表流水对两侧岸坡岩土体的长期侧蚀、浸泡和软化，增大了斜坡的临空面积，降低了岩土体强度，达到一定程度会失稳形成崩塌地质灾害（李信等，2022c）。由于坡脚的土体常年浸泡变软，土体强度逐渐降低，当土体重力大于其拉应力时，发生崩塌地质灾害（黄长生等，2002）。根据尖峰岭公园公路沿线水系对地质灾害的影响情况，本文将水系缓冲距离（单位：m）划分为[0，200）、[200，400）、[400，600）、[600，800）、[800，1000）、≥1000六个区间（图2e）。通过GIS 空间分析和叠加分析，统计水系不同缓冲距离内的地质灾害分布数量，并计算其敏感性指数。

由图3e 可以看出，地质灾害主要分布于距离水系800 m 以内，当水系缓冲距离逐渐增大时，地质灾害占比总体呈下降趋势。水系缓冲距离在1000 m 以上时仍可见一定数量的崩塌，主要是水系、沟壑两侧一定距离范围内修路或建房开挖边坡导致而成。故水系在一定程度上影响和控制了地质灾害发生的概率。

3.6 降雨量

海南岛地质灾害集中发生在7～10 月的汛期，主要是受风暴潮和强降雨的诱发，降雨量是诱发地质灾害的重要因素。尖峰岭公园公路沿线出露花岗岩风化土，其斜坡变形破坏与累积降雨量具有明显的相关性；斜坡变形破坏有一定的滞后性，滞后期为5～7 天。根据收集到的降雨量等值线图，本文将降雨量（单位：mm）分为[640，740）、[740，840）、[840，940）、[940，1040）四个区间（图2f）。

如图3f，尖峰岭公园公路沿线敏感性指数均为正，表明地质灾害在640～1040 mm 内降雨量对地质灾害发生的确定性高，在该范围内的降雨量条件易于发生地质灾害；敏感性指数随着降雨量的升高而逐渐升高，单从灾害点的占比来看，840～1040 mm地质灾害发生的概率较大。

4 地质灾害敏感性区划与评价

4.1 确定性系数模型

依据确定性系数公式（1），计算出评价因子的确定性系数值即为敏感性指数ICF。运用GIS空间分析功能，对评价因子图层进行叠加，按自然断点法将叠加图层进行划分，得出地质灾害敏感性评价区划图。

4.2 确定性系数逻辑回归模型

依据逻辑回归模型原理及公式,以确定性系数值作为逻辑回归模型的自变量，以地质灾害发生或不发生作为因变量进行逻辑回归运算。为满足逻辑回归模型样本点数量要求，文章利用GIS空间分析功能，生成420 个非灾害点，与原有的80 个地质灾害点共同组成500个逻辑回归样本。当运算的结果满足显著性水平小于0.05 时，统计具有意义，结果显示显著性均小于0.05（表1），满足要求。

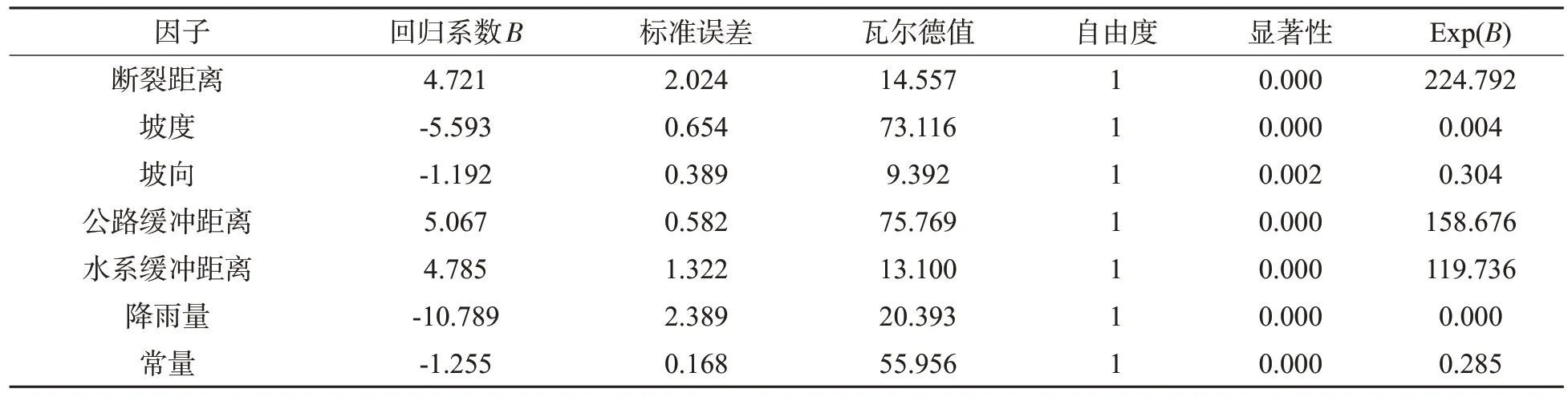
表1 逻辑回归运算结果Table 1 Logistic regression calculation results

表1 中的B 为逻辑回归模型的回归系数，刻画了评价因子确定性系数值（自变量）与是否发生地质灾害（因变量）之间的相关度，常量代表无其他因子影响时不发生地质灾害的相对程度。将逻辑回归系数加权相加、归一化运算后，分别得出了海南热带雨林国家公园公路沿线地质灾害敏感性评价六个因子之间的权重值，并依据权重大小进行排序（表2），影响因素对地质灾害发生概率的相关程度由大到小依次为：降雨量＞坡度＞公路缓冲距离＞水系缓冲距离＞断裂距离＞坡向。

表2 研究区地质灾害敏感性评价因子权重大小及排名Table 2 Weight and ranking of susceptibility evaluation factors of geohazards in study area

将回归系数B代入公式（2）可得出逻辑回归模型如下：

将回归系数归一化作为模型的权重，代入公式（3），可得出敏感性指数ICFLR。运用GIS空间叠加功能对因子图层叠加，采用自然断点分级法得到基于确定性系数与逻辑回归耦合模型（CFLR）的敏感性区划图。

5 地质灾害敏感性评价结果及检验

5.1 地质灾害敏感性评价结果

基于确定系数模型（CF）和确定性系数逻辑回归模型（CFLR），将易发性指数分别赋值评价因子图层，运用GIS 叠加分析功能和重分类功能，分别进行了地质灾害敏感性区划，形成了基于两种模型下的地质灾害敏感性区划图（图4）。

图4 研究区地质灾害敏感性评价因子叠加示意图及两种敏感性评价区划图Fig.4 Schematic diagram of the geohazard factors and zoning maps of two models of susceptibility evaluation in study area

根据两种模型评价结果，将尖峰岭公园公路沿线地质灾害敏感性等级分区划分为极低易发区、低易发区、中易发区和高易发区，其中，高易发区主要位于公路沿线地质灾害较发育的地段，极低和低易发区位于人迹罕至的高海拔地区。尖峰岭公园公路沿线地质灾害点数量由低到高分别分布在极低易发区、低易发区、中易发区和高易发区（表3），因此，两种评价模型结果都表明实际的地质灾害发育分布情况与评价结果基本吻合。将已发生的地质灾害点投入到敏感性分区得到CF 模型和CFLR 耦合模型高易发区的灾害点比例分别为67.50%和83.75%；在极低易发区的灾害点比例均为1.25%，在低易发区的灾害点占比分别为6.25%和5.00%（表3）。灾害点数量在CFLR 耦合模型中高易发区占比明显高于CF 模型，灾害点数量在低易发区占比CFLR 模型明显低于CF 模型，表明CFLR 模型预测灾害点的准确性高于CF 模型。

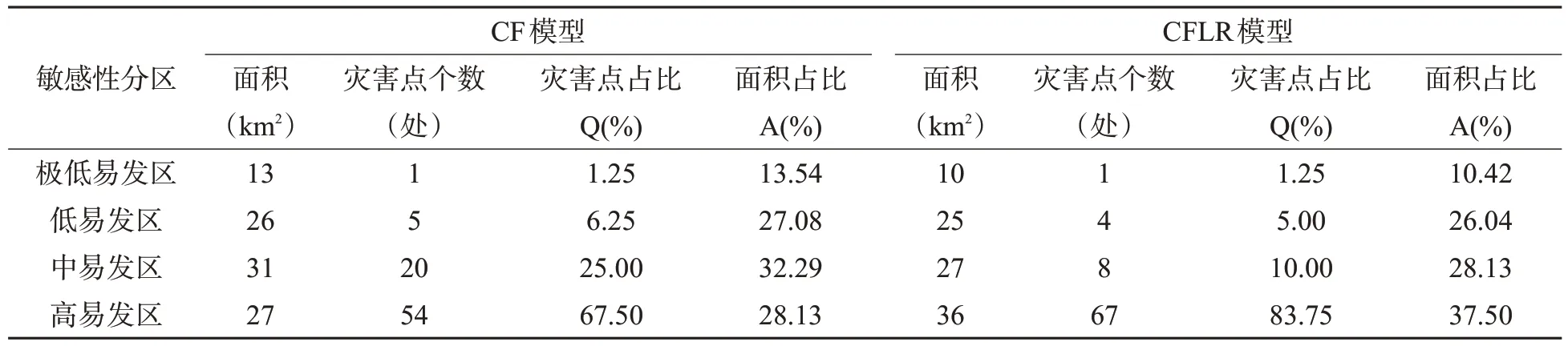
表3 研究区两种地质灾害敏感性评价模型检验结果对比Table 3 Comparison of test results of both evaluation models in study area

5.2 地质灾害敏感性结果检验

地质灾害敏感性评价结果的可靠性取决于模型的精度和敏感性，ROC 曲线被广泛应用于分析模型特异性和敏感性的关系，具有较强的可操作性和科学性（杨志华等,2018），ROC 曲线（受试者工作特征曲线，Receiver Operating Characteristic）是反映敏感性与特异性之间关系的曲线，横轴为1-特异性，也称为假阳性率（误报率），表示未发生灾害被正确预测的累计百分比；纵轴称为敏感度，也称为真阳性率，表示灾害单元被正确预测的累计百分比；ROC 曲线能够较为直观的以定量方式来描述预测模型的精度，使用AUC（曲线和横轴之间的面积，Area Under Curve）值来对模型进行准确的比较和衡量，其值介于0.5～1之间，越接近1，则精度越高（缪信等,2016）。运用SPSS 软件进行运算，CF模型和CFLR 模型的AUC 值分别为0.785、0.808（图5），表明两种模型均能客观准确的对尖峰岭公园公路沿线敏感性进行评价，然而在预测的精度上差异明显，预测效果准确性为确定性系数与逻辑回归耦合模型（CFLR）高于确定系数模型（CF）。

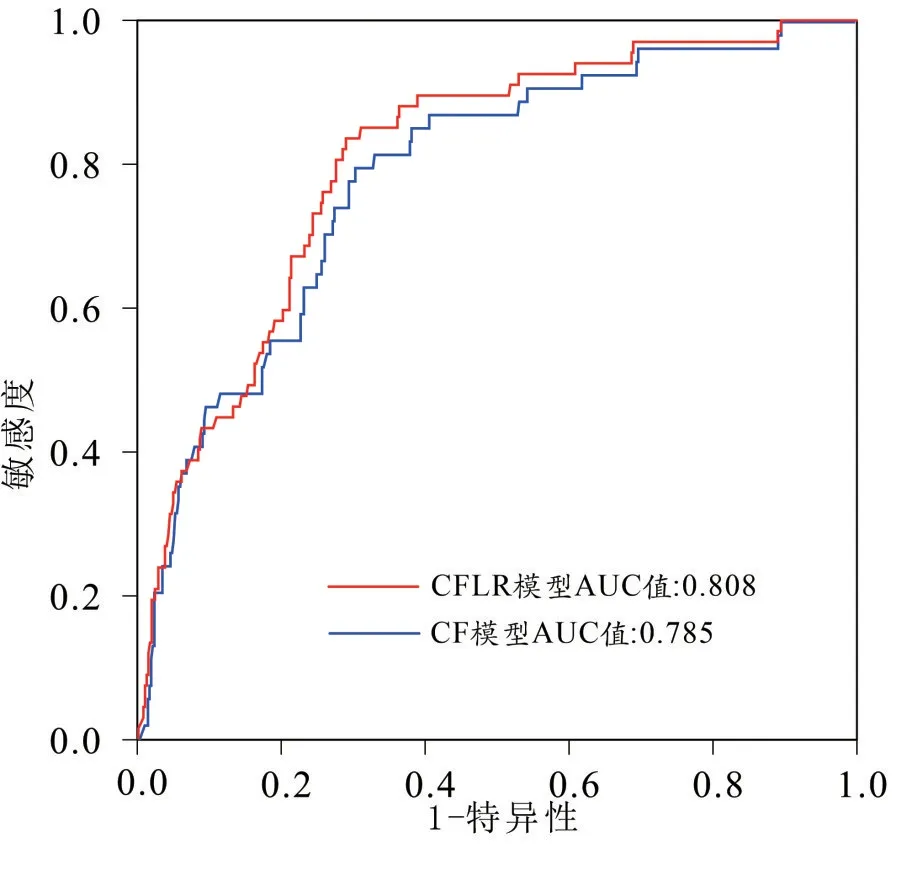
图5 研究区地质灾害敏感性预测ROC曲线Fig.5 ROC curve of geological hazard sensitivity prediction in study area

综上所述，基于两种模型对于海南热带雨林国家公园公路沿线进行地质灾害敏感性评价，其评价结果与海南热带雨林国家公园公路沿线地质灾害发育的实际情况基本一致，但确定性系数逻辑回归模型（CFLR）较单一的确定性系数法（CF）具有更高的准确度和可靠性。

6 结论

（1）海南热带雨林国家公园公路沿线地质灾害敏感性评价的六种影响因子中，断裂距离[3000 m，4000 m），坡度50°以上，坡向为北坡、东坡、南坡、西南坡，公路缓冲距离为[0 m，100 m），水系距离为[0 m，200 m）时，在各评价因子分级中敏感性指数较高，对地质灾害发育较为有利。评价因子对地质灾害的影响程度由大到小依次为降雨量＞坡度＞公路缓冲距离＞水系缓冲距离＞断裂距离＞坡向。

（2）海南热带雨林国家公园公路沿线地质灾害敏感性评价结果将该区地质灾害敏感性等级划分为极低易发区、低易发区、中易发区和高易发区，高易发区主要位于公路沿线地质灾害较发育的地段，极低和低易发区位于人迹罕至的高海拔地区。研究结果将为海南热带雨林国家公园公路沿线地质灾害敏感性识别、精准化监测与防灾减灾提供指导。

（3）评价结果与地质灾害发育分布情况基本吻合。评价模型的AUC值分别为0.785、0.808，均大于0.7，表明两种评价模型具有较好的可靠性和客观性；确定性系数逻辑回归模型（CFLR）相比单一的确定系数模型（CF）具有更高的准确率。