非充气轮胎弹性支撑体的疲劳寿命仿真分析研究

韩 雪，顾博超，刘 晨，叶 欣，卢咏来，李凡珠*

（1.北京化工大学 有机无机复合材料国家重点实验室，北京 100029；2.北京化工大学 材料科学与工程学院，北京 100029）

近年来科技飞速发展，传统充气轮胎难以满足人们对新型轮胎日益增长的要求。非充气轮胎的设计理念应运而生，目前非充气轮胎已成为轮胎行业重点研究的新一代产品。非充气轮胎的典型结构见图1[1]，它包括胎面、增强剪切带、弹性支撑体和轮辋4个部分。非充气轮胎弹性支撑体由高强度、高韧性、耐疲劳的橡胶材料制成，其取代了传统充气轮胎的气囊结构，避免了非充气轮胎爆胎和漏气等安全风险。非充气轮胎的接触压力和垂直刚度不再耦合，两者相对独立，仅通过调整弹性支撑体和剪切带的结构形式和尺寸参数就可以有效地、大范围地优化非充气轮胎的性能[2]。目前，米其林推出的Tweel和Uptis非充气轮胎走在行业前列，各种类型的新概念非充气轮胎得到了很大的发展[2-3]。

图1 全地形车辆用Tweel非充气轮胎Fig.1 Tweel non-pneumatic tire for all-terrain vehicle

动态工况下，疲劳性能既反映了轮胎的耐久性、安全性和可靠性等，又决定了其全生命周期成本。橡胶材料的疲劳失效问题复杂，橡胶产品的疲劳失效更是甚之。橡胶产品的实际疲劳性能测试需要结合其真实工况条件，所用人力和物力较大及时间较长。高效精准的有限元分析法对解析橡胶产品的疲劳失效和疲劳寿命有很大的帮助。

在有限元分析中，选用合适的网格并兼顾分析精度和计算效率是十分必要的。本工作基于橡胶材料的疲劳裂纹扩展理论和临界平面分析法，运用Abaqus和Endurica软件联合仿真，实现非充气轮胎弹性支撑体的疲劳寿命预测。本文先简要介绍橡胶材料的疲劳理论和有限元分析用网格类型，然后以三维Tweel非充气轮胎结构为分析对象，系统分析有限元网格类型及网格尺寸对非充气轮胎弹性支撑体的疲劳寿命的影响。

1 橡胶材料的疲劳理论

1.1 疲劳概念

疲劳是指材料在某点或某些点承受周期性应力，即在一定次数的循环加载作用下形成裂纹或完全断裂时材料发生结构破坏的发展过程[4]。橡胶材料的疲劳破坏过程既存在物理机械作用，又存在化学降解作用，是非常复杂的动态过程，因此橡胶材料的疲劳破坏机理十分复杂[5]。断裂力学理论[6]认为橡胶材料的疲劳破坏源于外加载荷作用，导致橡胶材料内部的微观裂纹即裂纹前兆体逐渐扩展直至破坏。

1.2 疲劳失效分析方法

通常情况下可以将橡胶材料的疲劳失效过程分为两个阶段[7]：一是裂纹萌生阶段，在此阶段萌生的裂纹肉眼看不见；二是裂纹扩展阶段，即成核的裂纹不断扩展直至失效。与裂纹萌生阶段和裂纹扩展阶段对应的分析方法分别称为裂纹萌生法和裂纹扩展法。

裂纹萌生法（S-N数据法）[8]是基于连续介质力学观点，建立材料的应力、应变或应变能等参数与疲劳裂纹萌生寿命之间的关系，得到S-N曲线，进而预测裂纹萌生寿命。其中，S为损伤因子，N为裂纹萌生寿命。S-N数据法概念简单，易于理解，但对于橡胶材料很难得到较为精确的S-N曲线，即橡胶材料的S-N数据法存在数据波动大、测试成本高的问题[5]。

裂纹扩展法（dc/dN-T数据法）[7，9]是基于断裂力学观点，给定材料的加载模式和引入初始裂纹，建立裂纹扩展速率与撕裂能之间的关系，从而预测特定裂纹的扩展过程。其中，dc/dN为疲劳裂纹扩展速率，T为撕裂能。dc/dN-T数据法是以单个裂纹的扩展为研究对象，从能量角度进行疲劳扩展寿命的预测，与S-N数据法相比，其理论研究更加深入，测试更为简单。在完全松弛的动态加载条件（最小载荷为0，最小载荷与最大载荷之比R为0）下，最常用且最简单的疲劳裂纹扩展法则为Thomas模型[10]，其表达式如下：

式中，r为裂纹扩展速率，rc为临界裂纹扩展速率，Tc为临界撕裂能，F为幂率指数。rc和F可通过疲劳裂纹扩展试验得到[11]，rc是Tc对应的裂纹扩展速率。

1.3 疲劳寿命预测方法

橡胶材料的疲劳寿命是疲劳失效过程中两个阶段所对应的裂纹萌生寿命与裂纹扩展寿命之和[7]。在理解橡胶材料的疲劳破坏机理基础上，W.V.MARS[12-14]采用临界平面法、dc/dN-T数据法和雨流计数法等研究了多轴载荷条件下橡胶材料的疲劳过程，提出了橡胶材料的裂纹萌生寿命计算方法。这些课题以开裂能密度代替应变能密度作为基本判据，结合裂纹扩展模型和疲劳数据，将疲劳寿命最短的平面作为裂纹扩展平面，在多轴复杂载荷作用下对橡胶材料的疲劳寿命进行预测。在此基础上，W.V.MARS综合多种因素对橡胶材料的疲劳寿命的影响，开发了Endurica软件，其用于橡胶材料疲劳寿命的有限元分析。

本工作首先对非充气轮胎弹性支撑体橡胶材料进行单轴拉伸、平面拉伸和双轴拉伸的应力-应变关系测试，基于拟合效果筛选出超弹性本构方程及其材料参数；然后基于Thomas疲劳裂纹扩展理论[10]，得到相应加载条件下橡胶材料的Tc，rc和F等参数，确定橡胶材料内部裂纹前兆体的长度（c0）和橡胶材料失效对应的临界裂纹长度（cf），认定裂纹从c0增长至cf时橡胶材料发生了疲劳失效；最后采用Abaqus和Endurica软件进行联合仿真计算，得到非充气轮胎弹性支撑体的疲劳寿命仿真结果。

2 网格划分

在有限元分析中，三维连续体单元主要包括四面体、楔形和六面体3种形状。按照节点位移插值的阶数，将单元分为线性单元和二次单元。而根据单元的积分，可以分为完全积分单元和减缩积分单元。三维连续体单元的网格类型如表1所示，不同网格类型单元对应的节点分布如图2所示。

表1 三维连续体单元的网格类型Tab.1 Mesh types of 3D continuum cells

图2 不同网格类型单元对应的节点分布Fig.2 Node distributions corresponding to cells of different mesh types

以C3D8RH网格单元为例，C表示连续体单元，3D表示三维，8表示节点个数，R表示减缩积分，H表示杂交单元。C3D8RH表示8节点六面体线性减缩积分单元。

种子是网格划分中沿区域边缘放置的标记，能够控制节点的位置和密度。沿区域边缘的种子决定了沿区域边界以及区域内部的网格密度。本研究通过设置全局种子的大小即网格尺寸来调整网格密度。

3 非充气轮胎模型的建立与有限元分析

3.1 几何模型和材料模型

建立如图3所示的非充气轮胎三维模型，主要包括胎面、增强剪切带、轮辋、弹性支撑体、弹性支撑体内覆盖层和弹性支撑体外覆盖层6个部分，其中弹性支撑体是重点研究对象。在此基础上建立路面部件，以实现工况条件的有效施加。非充气轮胎的三维模型参数如表2所示。

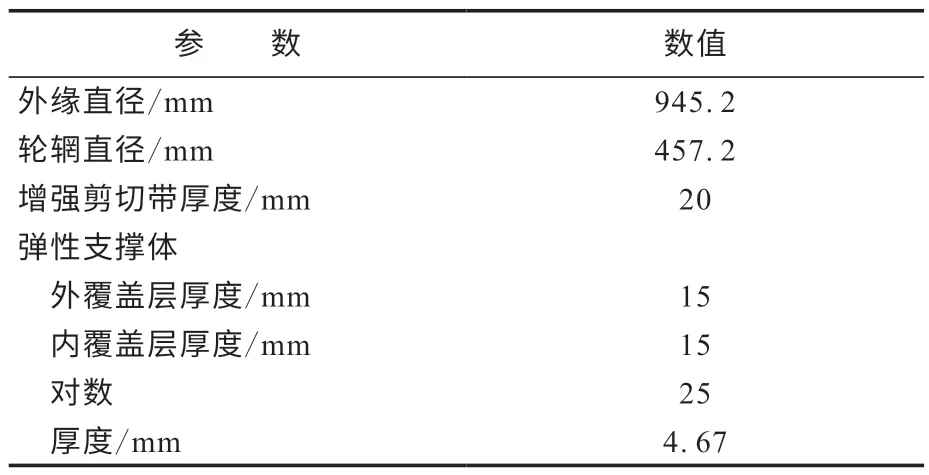
表2 非充气轮胎的三维模型参数Tab.2 3D model parameters of non-pneumatic tire

图3 非充气轮胎的三维模型Fig.3 3D model of non-pneumatic tire

非充气轮胎弹性支撑体橡胶材料的模型选用六阶Ogden超弹性本构方程，表达式如下所示：

式中：W为应变能密度；λ为拉伸比，其下标1，2，3分别表示3个主方向；µi和αi为材料常数。

弹性支撑体橡胶材料的六阶Ogden超弹性本构方程的材料参数如表3所示。

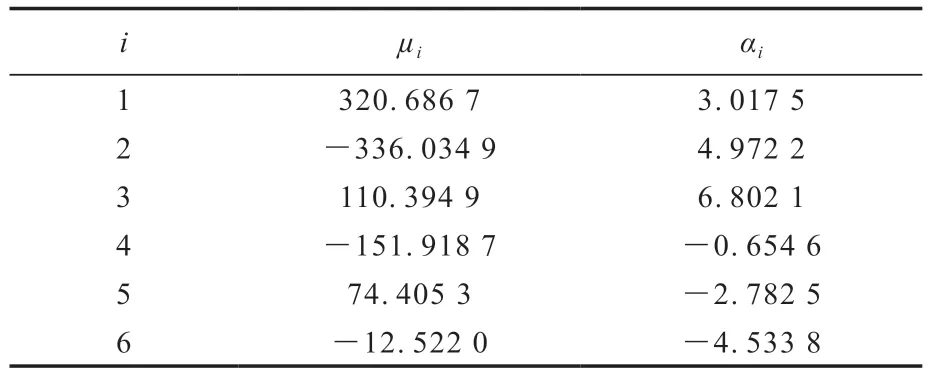
表3 弹性支撑体橡胶材料的六阶Ogden超弹性本构方程的材料参数Tab.3 Material parameters of sixth order Ogden hyperelastic constitutive equation of elastic spoke rubber material

3.2 边界条件设置及网格划分

将弹性支撑体和增强剪切带等各相互接触的部件通过约束和耦合等多种作用力连接，设置路面与胎面之间的接触；边界条件为地面向上20 mm位移。对每一部件依次进行网格划分，除弹性支撑体外，胎面、增强剪切带、弹性支撑体外覆盖层和弹性支撑体内覆盖层均使用C3D8RH网格类型，根据不同部件的特征属性设置合适的网格密度。在其余部件网格划分条件一致的情况下，按照表1所示8种网格类型对弹性支撑体进行网格划分，每种网格类型对应10，11，12，13 和14 mm共5种网格尺寸。不同网格类型和不同网格密度共对应40种弹性支撑体模型，从而可得到网格划分对弹性支撑体仿真分析结果的影响。

非充气轮胎网格划分及弹性支撑体不同类型网格划分示意如图4所示。

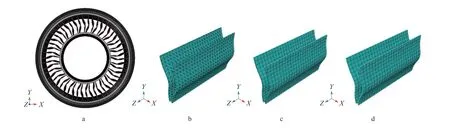
图4 非充气轮胎网格划分及弹性支撑体不同类型网格划分示意Fig.4 Schematic diagram of non-pneumatic tire mesh generation and different type mesh generations of elastic spokes

3.3 疲劳参数设置

基于Thomas模型理论，设置疲劳参数如下[15]：Tc＝30 mJ·mm-2，rc＝5.908×10-5mm·r-1，F＝1.085，c0＝0.025 mm，cf＝1 mm。

4 结果与讨论

4.1 力学响应分析

当网格密度相同（网格尺寸均为12 mm）时不同网格类型的弹性支撑体的位移云图如图5所示。

图5 不同网格类型弹性支撑体的位移云图Fig.5 Displacement nephograms of elastic spokes with different mesh types

从图5可以看出，不同网格类型的弹性支撑体的最大位移差异较大，其中C3D4H，C3D6H和C3D8H网格的弹性支撑体的最大位移分别为4.218，2.687和7.586 mm，小于其他5种网格类型的弹性支撑体，同时C3D8RH，C3D20H和C3D20RH网格的弹性支撑体的最大位移相近。可见不同网格类型对弹性支撑体的位移云图有一定影响。

力-位移曲线可以反映弹性支撑体在不同负荷下的位移变化，其斜率代表垂向刚度。当网格密度相同（网格尺寸均为12 mm）时不同网格类型的弹性支撑体的力-位移曲线如图6所示。

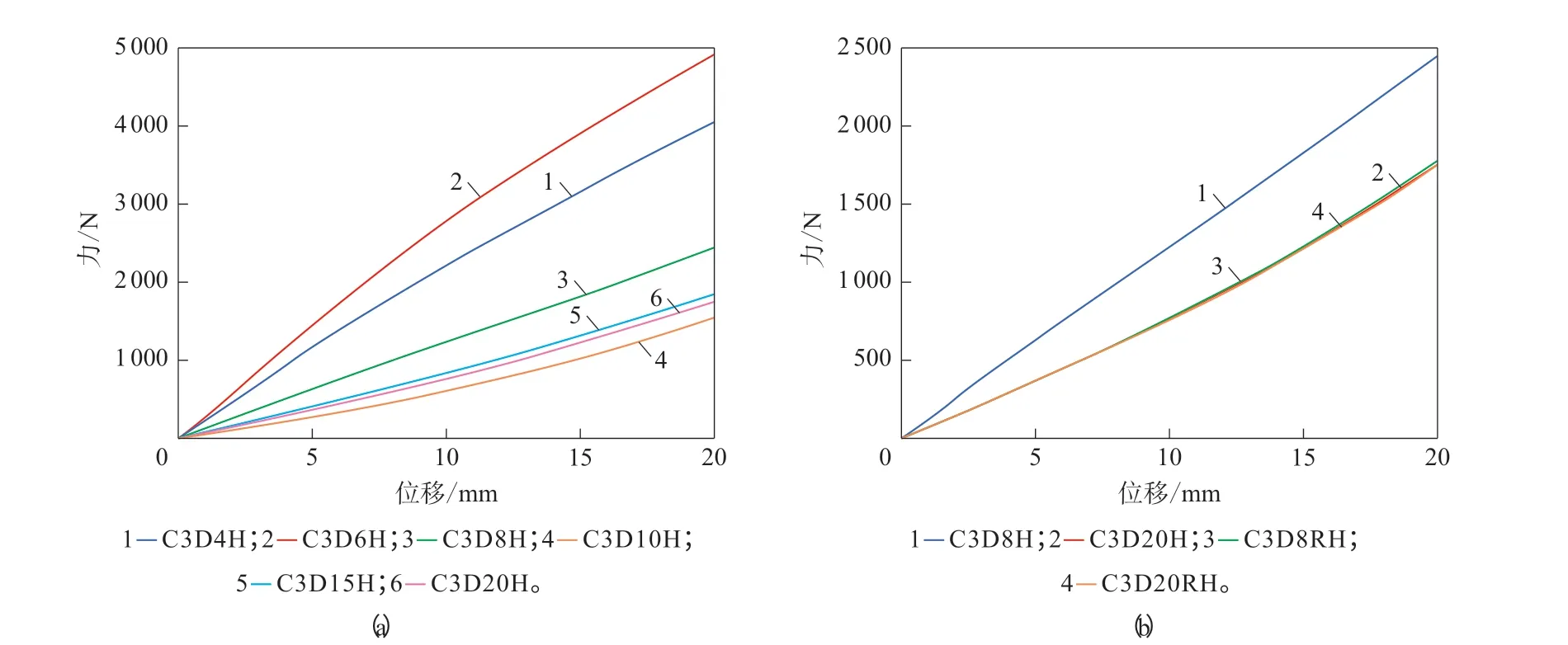
图6 不同网格类型的弹性支撑体的力-位移曲线Fig.6 Force-displacement curves of elastic spokes with different mesh types

从图6（a）可以看出：C3D6H，C3D4H 和C3D8H三种线性网格类型的弹性支撑体的力-位移曲线斜率依次减小，且降幅较大；C3D10H，C3D15H和C3D20H三种二次网格类型的弹性支撑体的力-位移曲线斜率基本一致，且均小于线性网格类型的弹性支撑体。从图6（b）可以看出，C3D8RH，C3D20H和C3D20RH网格的弹性支撑体的力-位移曲线几乎一致。整体来看，不同网格类型对非充气轮胎力学响应结果有一定影响。

C3D8RH网格的弹性支撑体在不同网格密度下的力-位移曲线如图7所示。从图7可以看出，网格尺寸为10～14 mm时网格密度对非充气轮胎力学响应结果的影响很小。

图7 C3D8RH网格弹性支撑体在不同网格密度下的力-位移曲线Fig 7 Force-displacement curves of elastic spokes with C3D8RH meshes under different mesh densities

在有限元分析中，计算时间也是重要的参考指标。弹性支撑体的网格类型/网格尺寸-力学响应计算时间曲线如图8所示。

图8 弹性支撑体的网格类型/网格尺寸-力学响应计算时间曲线Fig.8 Mesh type/mesh size-mechanical response calculation time curves of elastic spokes

从图8可以看出：当网格密度相同时，减缩积分网格的弹性支撑体的力学响应计算时间总体短于完全积分网格的弹性支撑体，线性网格的弹性支撑体的力学响应计算时间短于二次网格的弹性支撑体；二次网格的弹性支撑体的力学响应计算时间受网格密度影响较大，因此二次网格的弹性支撑体对力学响应计算时间的敏感度较大；C3D8RH网格的弹性支撑体的力学响应计算时间最短，且其网格密度对计算时间几乎没有影响。

4.2 疲劳寿命仿真分析

使用Endurica软件计算得到的弹性支撑体的疲劳寿命仿真结果如表4所示，不同网格类型的弹性支撑体（网格尺寸均为12 mm）的疲劳寿命云图如图9所示。

表4 弹性支撑体疲劳寿命的仿真计算结果Tab.4 Simulation and calcuation results of fatigue lives of elastic spokes

图9 不同网格类型的弹性支撑体的疲劳寿命云图Fig 9 Fatigue life nephograms of elastic spokes with different mesh types

从表4和图9可以看出，当网格密度相同时，不同网格类型的弹性支撑体的疲劳寿命分布存在差异，可见不同网格类型对疲劳寿命仿真计算结果有一定的影响。

弹性支撑体的疲劳寿命与计算时间的散点如图10所示。

图10 弹性支撑体的疲劳寿命与计算时间的散点Fig.10 Scatters of fatigues lives and calculation time of elastic spokes

从图10（a），（b）和（c）可见：当网格密度相同时，线性网格与二次网格的弹性支撑体的疲劳寿命差别较小；节点总数越多、网格密度越大，疲劳寿命计算时间越长；六面体网格的弹性支撑体的疲劳寿命明显长于四面体和楔形网格的弹性支撑体。

从图10（d）和（e）可见：当网格密度和节点总数相同时，减缩积分网格的弹性支撑体的疲劳寿命略长于使用完全积分网格的弹性支撑体；六面体网格的弹性支撑体的疲劳寿命差距较小，计算时间较短。

从图10（f）可见，C3D8RH和C3D20RH网格的弹性支撑体的疲劳寿命及计算时间均基本一致，更是推荐C3D8RH网格类型。

从图10整体可见：六面体网格的弹性支撑体的疲劳寿命计算结果较四面体和楔形网格的弹性支撑体更加稳定，计算时间更短；当网格类型相同时，弹性支撑体的疲劳寿命随网格密度的变化不敏感。

5 结论

（1）基于橡胶疲劳裂纹扩展理论和临界平面疲劳分析法，运用Abaqus和Endurica软件联合仿真的有限元分析法，对非充气轮胎弹性支撑体的疲劳寿命进行了仿真分析。在后续研究中还需要对非充气轮胎其他部件以及整个非充气轮胎的疲劳寿命进行仿真分析。

（2）在非充气轮胎弹性支撑体的疲劳寿命的有限元分析中，网格类型与网格密度对仿真结果均有一定影响。对于本研究的非充气轮胎三维模型，六面体网格的弹性支撑体的疲劳寿命计算结果较四面体网格和楔形网格的弹性支撑体受网格密度影响更小，垂向刚度计算结果更稳定。其中，C3D8RH网格的弹性支撑体的疲劳寿命和垂向刚度计算结果更是对网格密度不敏感，计算时间最短。

（3）本工作未对热力耦合条件下非充气轮胎弹性支撑体的疲劳寿命进行仿真分析，后续可以将此作为进一步的研究方向。