周向对称零件分析模型及约束、加载方法研究

黄云霞 郭越江 窦柏通

（中国航发商用航空发动机有限责任公司，上海 200241）

0 引言

在工程中有很多构件，如车床的光杆、搅拌机轴、汽车传动轴等，都是受扭构件。在使用有限元对这些受扭构件进行静强度分析时，如果用整圈模型进行计算，约束及加载相对容易，但是网格数量大，需要的计算资源多；若网格数量少，则计算精度不够。因此，一般采用扇形段模型来进行模拟，但扇形段模型的边界条件和载荷施加方法不能按照整圈模型来加载。本文尝试了各种整体模型和扇形段模型的约束及加载方法，为结构受力与变形分析提供依据[1]。

1 理论

扭矩是刚体发生扭转变形的动力，扭矩实际上是一力偶矩。在实际分析过程中，将受扭构件一端约束，另一端施加扭矩。

在进行受扭构件静力分析时，需要对受扭杆件的扭转变形进行平面假设，即扭转变形前后截面的大小形状均不变，相邻两个截面间的距离不变。物理依据是剪切胡克定律，即剪应力和角应变成正比，系数为材料的剪切弹性模量。静力关系主要是通过微积分形式来表示扭矩，进而确定最大应力。变形几何关系和静力关系推出的扭转角公式为：

式中：θ为扭转角；M为扭矩；G为剪切弹性模量；I为对称中心的惯性距。

根据物理关系，得出剪应力计算公式为：

式中：τ为剪切应力；M为扭矩；W为抗弯截面系数[2]。

2 计算模型

几何模型直径120 mm，长度100 mm，厚度2 mm，密度7.8×103kg/m3，弹性模量为195 000 MPa。共有4个有限元模型：

1）整圈模型周向均匀网格，如图1所示；

图1 整圈模型周向均匀网格

2）整圈模型周向非均匀网格，如图2所示；

图2 整圈模型周向非均匀网格

3）扇形段模型周向均匀网格，如图3所示；

图3 扇形段模型周向均匀网格

4）扇形段模型周向非均匀网格，如图4所示[3-5]。

图4 扇形段模型周向非均匀网格

3 网格及扭矩加载方式

针对第2章描述的4个有限元模型，本文尝试了10种扭矩加载方式：

方式一：整圈模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端在端点施加节点力。

方式二：整圈模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端在截面中心点处施加扭矩。

方式三：整圈模型周向非均匀网格，在模型的一端进行轴向和周向约束，另一端在截面中心点处施加扭矩。

方式四：扇形段模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端在端点施加节点力，在对称面上设置循环对称约束。

方式五：扇形段模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端在截面中心点处施加扭矩，在对称面上设置循环对称约束。

方式六：扇形段模型周向非均匀网格，在模型的一端进行轴向和周向约束，另一端在截面中心点处施加扭矩，在对称面上设置循环对称约束。

方式七：整圈模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端通过控制点建接触的方法施加扭矩，相当于在实际受载荷区域建立一个刚性区域，然后把载荷施加在跟这个刚性区域连接的“pilot node”上。

方式八：整圈模型周向非均匀网格，在模型的一端进行轴向和周向约束，另一端通过控制点建接触的方法施加扭矩，相当于在实际受载荷区域建立一个刚性区域，然后把载荷施加在跟这个刚性区域连接的“pilot node”上。

方式九：扇形段模型周向均匀网格，在模型的一端进行轴向和周向约束，另一端通过控制点建接触的方法施加扭矩，相当于在实际受载荷区域建立一个刚性区域，然后把载荷施加在跟这个刚性区域连接的“pilot node”上。

方式十：扇形段模型周向非均匀网格，在模型的一端进行轴向和周向约束，另一端通过控制点建接触的方法施加扭矩，相当于在实际受载荷区域建立一个刚性区域，然后把载荷施加在跟这个刚性区域连接的“pilot node”上。

方式一至方式十的有限元模型及扭矩加载方式如表1所示。

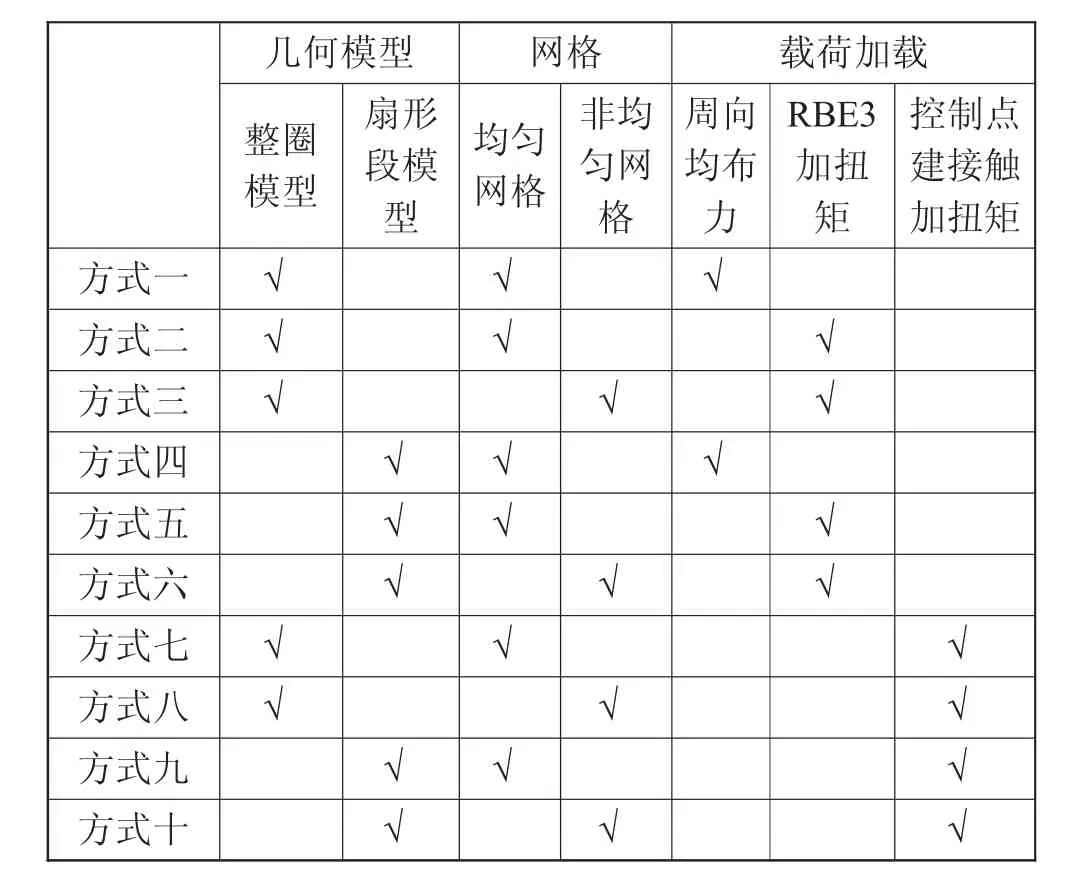
表1 有限元模型及扭矩加载方式

4 计算结果

以周向变形结果为目标，以上各种加载方式下的计算结果如图5～14所示。

图5 方式一周向变形

图6 方式二周向变形

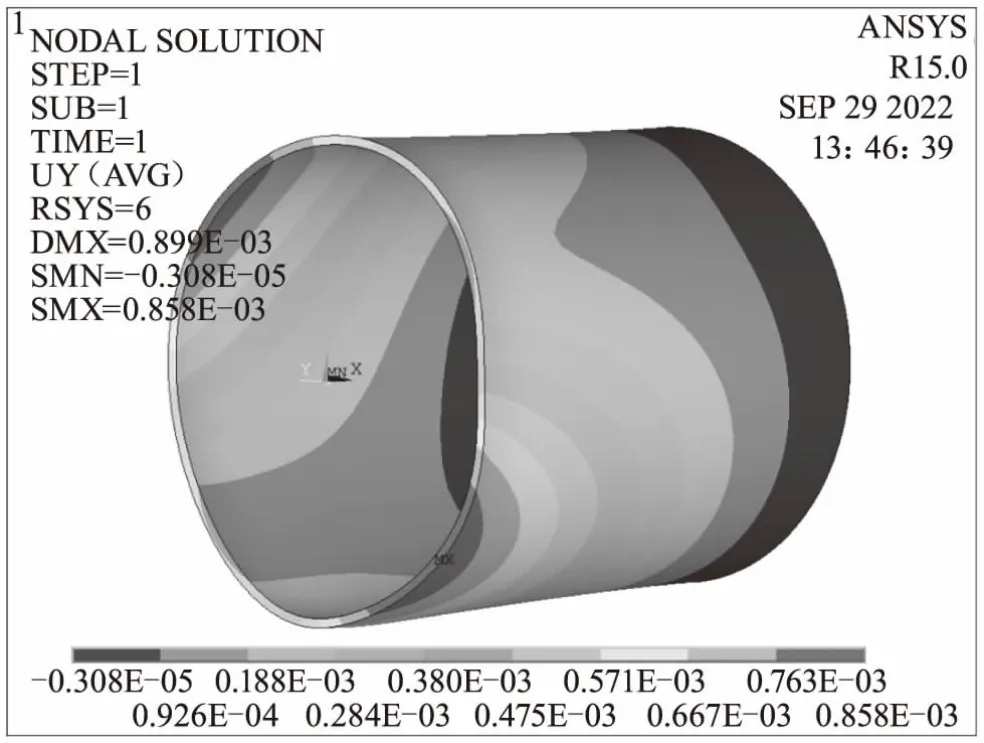
图7 方式三周向变形

图8 方式四周向变形

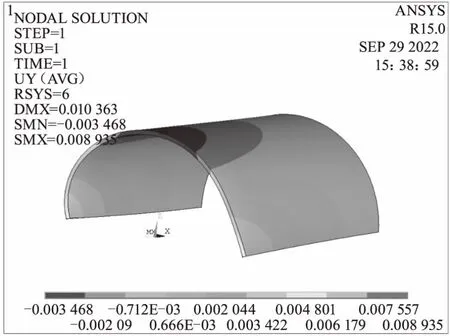
图9 方式五周向变形

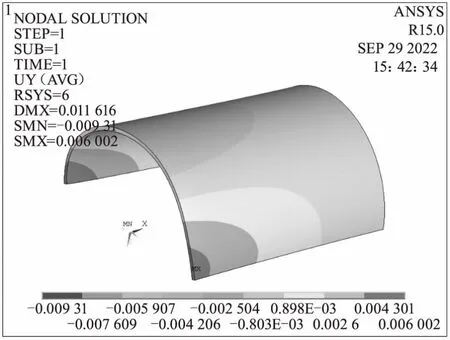
图10 方式六周向变形

图11 方式七周向变形

图12 方式八周向变形

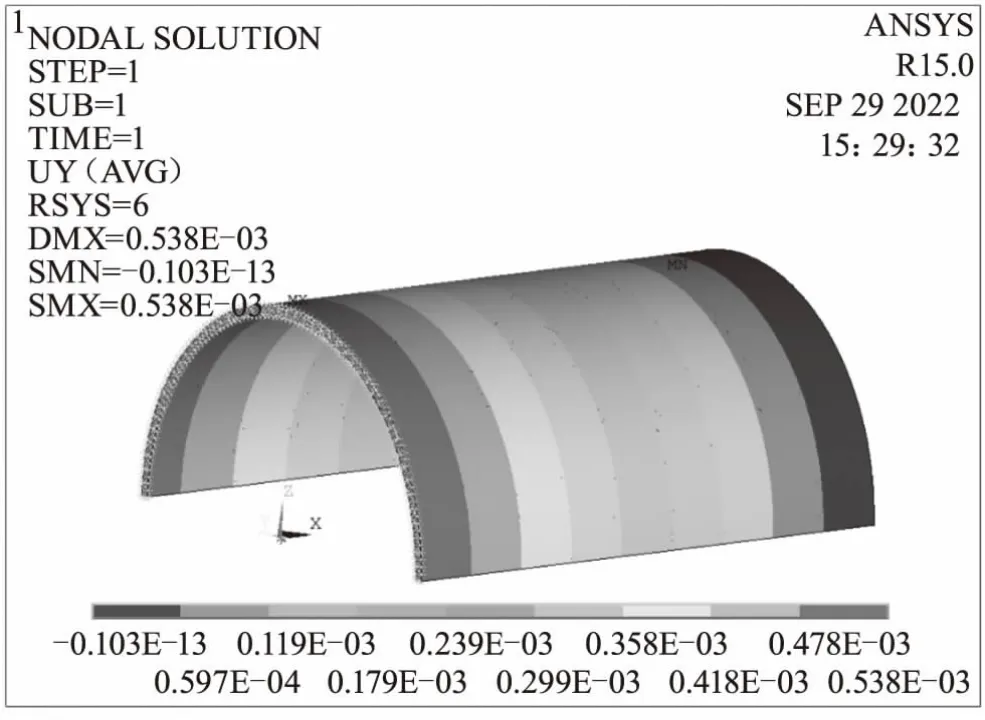
图13 方式九周向变形

图14 方式十周向变形

从图5～14和表2可以看出：

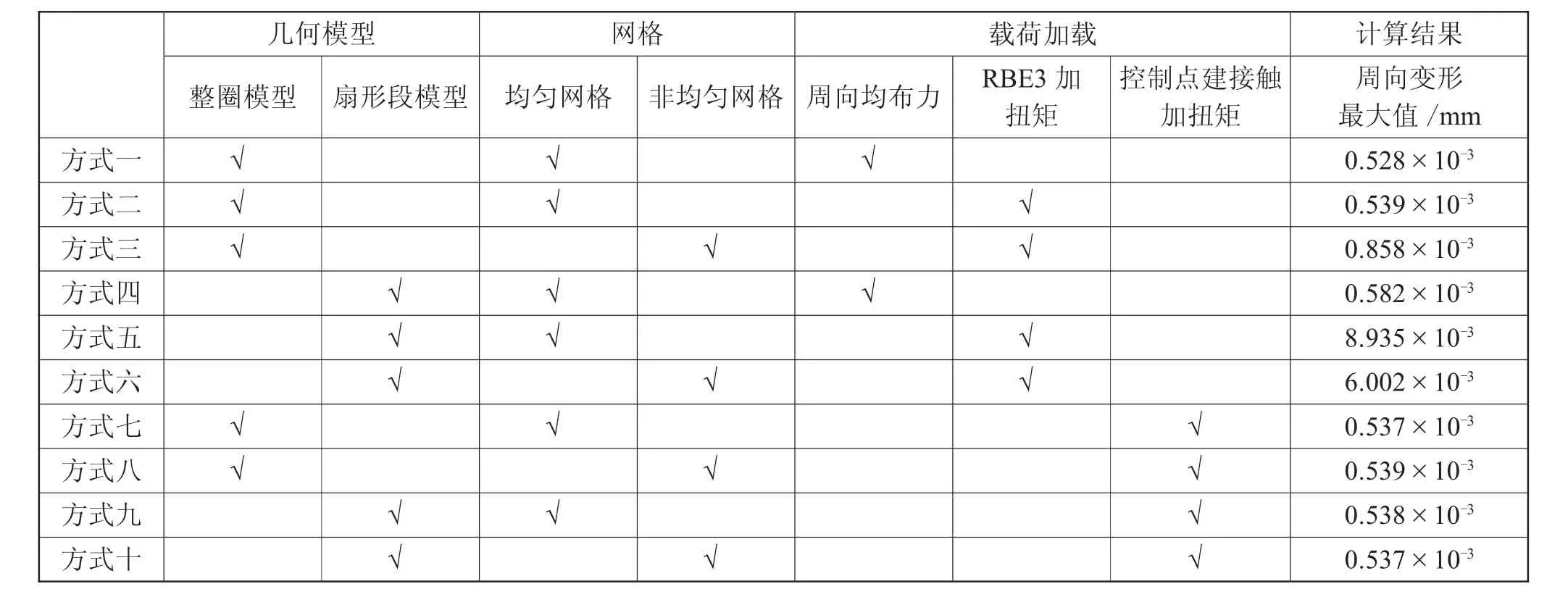
表2 有限元模型及扭矩加载方式

1）整圈模型用周向均匀网格对模型进行离散，在末端加周向力和通过RBE3在中心点加扭矩的方式得到的结果一致；

2）整圈模型用周向非均匀网格对模型进行离散，在末端通过RBE3在中心点加扭矩的方式得到的结果和整圈模型周向均匀网格得到的结果不一致；

3）扇形段模型用周向均匀网格对模型进行离散，在末端加周向力得到的结果和整圈模型周向均匀网格得到的结果一致；

4）扇形段模型用周向非均匀网格对模型进行离散，通过RBE3在中心点加扭矩，得到的计算结果和整圈模型周向均匀网格的结果不一致；

5）扇形段模型用周向非均匀网格对模型进行离散，在末端通过RBE3在中心点加扭矩得到的计算结果和整圈模型周向均匀网格的结果不一致；

6）整圈模型用周向均匀网格和周向非均匀网格对模型进行离散，通过控制点建接触在控制点加扭矩，得到的计算结果和整圈模型周向均匀网格的结果一致；

7）扇形段模型用周向均匀网格和周向非均匀网格对模型进行离散，通过控制点建接触在控制点加扭矩，得到的计算结果和整圈模型周向均匀网格的结果一致。

5 结论

针对各种有限元模型及扭矩加载方式，基于周向变形计算结果，得到的结论如下：

1）整圈模型均匀网格，可以用截面节点周向力、RBE3和控制点建接触的方式施加扭矩；

2）整圈模型非均匀网格和扇形段模型（循环对称边界）只能用控制点建接触的方式施加扭矩，计算结果与整圈模型均匀网格一致。

因此，结合计算效率，建议采用扇形段模型周向非均匀网格开展周向对称零件的有限元分析。