借图示表征,解“烙饼问题”
2023-12-25潘冰宁付芳
潘冰宁 付芳


[摘 要]图示表征可以使抽象的数学概念具体化、可视化,帮助学生更好地理解和运用数学知识。以北师大版教材四年级下册“烙饼问题”为例,从找准课堂教学起点、突破学生学习难点、关注数学学习节点和助力学生达成学习目的四个方面,谈一谈如何利用图示表征解决“烙饼问题”教学中的难点,使学生在不同要求的图示表征中有所思、有所想、有所悟。
[关键词]图示表征;烙饼问题;优化
[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068(2023)29-0059-04
图示是指使用图表、图形、图像或其他可视化方式来呈现信息、数据、概念或思想的过程。图示表征可以将问题可视化,促进思考、沟通联系、分析问题。如图1所示,“烙饼问题”的目的是通过生活中常见的烙饼问题,让学生经历探索多种解决方案的过程,从而选择最优方法,渗透优化思想。
在教学中,部分教师容易将“烙饼问题”上成一节“探索规律—发现规律—总结方法”的课,课堂氛围虽一片热闹,但缺乏冷静思考。这导致学生仅仅学会套用方法,虽得其法却不解其意,一旦变换题型就会束手无策。过于热闹的课堂和过于冷静的课堂都不是好的教学状态。因此,教师需要在必要的时机对学生的热闹进行“冷处理”,利用图示表征提高解决问题的效率。
一、利用图示表征理解题意,找准课堂教学起点
如果说智慧的大脑是解决问题的关键,那么理解题意就是解决问题的开端。在生活中,多数学生都会烙饼,但是将烙饼和数学相结合还是第一次,这也是让学生体会数学与生活密切联系的契机。因此,读懂题意在此时显得尤为重要。
【教学片段1】
师:“每次只能烙2张饼”是什么意思?
生1:锅里最多同时放2张饼。
师:请你上来画一画。
(生1画出如图2所示的图形)
师:“两面都要烙”是什么意思?
生2:一张饼有两个面,如果用正面、反面表示,出现“正”字表示烙正面,出现“反”字表示烙反面(如图3)。
师:根据他们说的这些数学信息,你能提出什么问题?
生3:烙3张饼要多长时间?
生4:烙3张饼至少要多长时间?
师:大家的理解能力越来越好了。烙3张饼可能要1个小时或1天,而加了“至少”,说明你们用数学的眼光去看待问题了。
【教学思考】教材中所给的情境看似贴近生活實际,实则离生活还有一定距离,因为生活中很少有或者说基本没有关注烙饼要多久的问题。教师要帮助学生梳理图中的信息,找到题眼——“每次只能烙2张”“两面都要烙”。在这一过程中,虽然可以让学生用自己的话说一说,但是利用锅和饼的图示表征会更直观,也更具说服力。教师利用图示慢慢地剥离问题的生活情境,让学生集中思考“烙3张饼至少要多长时间”。这有助于学生直观地理解问题的本质、结构和关系,从而更好地把握问题的核心。
二、利用图示表征寻找方法,突破学生学习难点
直接进入“烙3张饼至少要多长时间”对学生而言有些难以接受,因此教师可以从最基础的烙1张饼开始,利用表格表示烙饼过程(正面3分钟,反面3分钟,一共6分钟)。紧接着让学生思考烙2张饼的方法,这时候可能有学生受思维的局限,出现表1-1的方法,也有学生经过思考后给出表1-2的方法。
【教学片段2】
师:谁看懂了表1-1和表1-2中的烙法?
生1:表1-1的方法是锅里每次放1张饼,2张饼烙完一共12分钟;表1-2的方法是锅里每次放2张饼,2张饼烙完一共6分钟。
生2:为什么烙1张饼是6分钟,烙2张饼也是6分钟?
生3:因为2张饼可以同时放在锅里一起烙。
师:也就是说,要想烙饼所用时间最少,就要保证锅里每次都有2张饼。怎样将表1-1的方法进行调整,才能做到用时最少呢?
(学生进行调整,见表2-1、表2-2)
师:调整后的方法(见表2-2)对吗?
生4:不对,因为1张饼不可能同时烙两个面,只能是先烙完一面再烙另一面。
【教学思考】烙1张饼很简单,烙2张饼的时候有的学生就忽略了“每次只能烙2张饼”的信息,才会产生1张1张地烙的想法。此时,教师就需要及时借助图示,让这些学生学会2张饼同时烙的省时方法。让学生经历修正的过程,也是拉长学生思考的过程。在这个过程中让学生感受只有在“满锅”的状态下才最节省时间,提高学生思维的缜密性。这种思想也影响着接下来烙3张饼的方法。解决“烙饼问题”时,利用图示表征方法能够有效地帮助学生克服难点,为问题的理解和解决提供了强有力的工具。
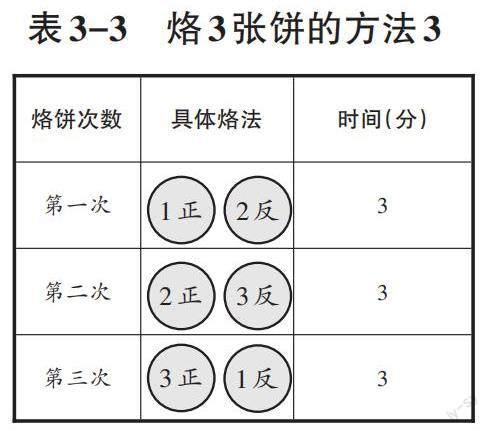
学生想到的烙3张饼的方法有很多,教师可选择以下三种情况(见表3-1、表3-2、表3-3)来给学生讲解。对第一种烙法教师进行肯定,因为在一定程度上达到了节省时间的目的。对第二种烙法,教师需要学生回顾“1张饼不可能同时烙两个面”这个原则,以强化学生的优化意识。
【教学片段3】
师(出示表3-3):像他这么烙,烙几次?
生5:3次。
师:除了这么烙还能怎么烙?
生6:“3反”和“2反”互换位置。
生7:“1正”和“1反”互换位置。
师:结合大家的方法,谁还有什么想说的?
生8:只要保证不出现同时烙1张饼的两个面,其他怎么烙都行。
师:现在请你们利用手中的学具,一边画一边说3张饼怎么烙3次的情况。
【教学思考】教师在教学过程中要善于倾听学生不同的声音。将烙3张饼的方法按照顺序依次出现,是符合学生的知识发展和心理特点的。而交替式的烙饼方法是学生思考由浅入深的必然过程。相信当学生看到不同的图示时,都会有自己的观察、比较、思考在其中。让每个学生都能有所发展正是数学学习的意义所在。学生在经历烙2张饼后,一定会对烙3张饼有不一样的思考,教师应充分相信学生,充分相信合作的力量,给予学生充足的时间和空间去探索、去发现。
烙3张饼很难突破,只有让学生直面教学难点,才能留下思考的痕迹。在这个环节中,利用图示,学生可以直观看到烙饼的方法,进而发现烙饼问题中的规律、模式及瓶颈,为问题求解提供新的思路和启示。
三、利用图示表征辨别优化,关注数学学习节点
当学生明白2张饼、3张饼的烙法后,心中必然是有所得意,教学也进入白热化阶段。教师可相机提出“烙4张饼最少要用几分钟”。教师巡视发现,有学生选择2张2张地烙(见表4-1),有学生受烙3张饼的影响用交替烙的方法(见表4-2)。教师让学生比较两种方法,大部分学生觉得交替烙的方法劳心费神,且容易出错。
【教学片段4】
师:烙5张饼怎么烙呢?最少要用几分钟?
生1:先按顺序烙2张,再用交替法烙3张,一共烙5次,用时15分钟。
[烙饼次数 具体烙法 时间(分) 第一次 3 第二次 3 第三次 3 第四次 3 第五次 3 ] [1正] [1反] [2正] [2反] [3正] [4反] [4正] [5正] [3反] [5反]
师:烙6张饼呢?
生2:2张2张地烙,一共烙6次,共用3×6=18(分)。
师:烙7张饼呢?
生3:按顺序2张2张地烙,烙4张后,剩下的3张用交替法烙3次。
师:这么多饼都烙完了,你觉得烙几张饼对我们解决问题最重要?
生4:烙3张,我从中知道了交替烙的方法。
生5:我觉得烙2张饼也很重要。
师:为什么?
生5:如果没有烙2张饼的方法总结,就解决不了烙5张饼的问题。
师:掌声送给会思考的孩子。
(教师继续教学烙6张饼、7张饼以及9张饼)
【教学思考】对比烙4张饼的2种方法,让学生打破思维定式进一步感受“优化”。有了这样的体验,学生在思考烙5张饼时,会将思考的重心放在如何缩短时间上,进而发现烙2张和烙3张的重要意义,为后面用最少的时间烙更多的饼打下坚实的基础。在烙饼问题中,图示表征的优势显而易见。通过简洁明了的图示,学生可以直观地观察每次烙饼的结果,无须进行烦琐的计算,进而快速找到最优策略。此外,随着饼的数量的增加,图示的优势更加凸显,因为在复杂的烙饼序列中,图示可以帮助学生更好地跟踪和分析每一步的操作,也更容易发现问题中的关联性,从而更全面地理解烙饼问题的整体架构。
四、利用图示表征拓展思维,助力学生达成学习目的
烙饼问题是有规律可循的,而有的教师仅仅通过简单的讲解便将公式“灌输”给学生。正确的教学方法应该是教师通过层层铺垫,化繁为简,从简单的烙1张饼开始教学,到烙2张饼、3张饼,以及烙更多的饼。当学生意识到烙更多饼的方法可以总结成一个公式时,就是揭示烙饼问题背后规律的最佳时机。
【教学片段5】
师:在烙饼的时候,你有什么新的发现吗?
生1:有几张饼就要烙几次。
师:为什么烙的次数和饼的张数相同呢?
生2:烙饼的时候,每次烙2个面,2个面就是1张饼。
生3:因为我们要利用锅的最大空间,如果一个锅一次可以烙 2 张饼,那么烙饼次数=饼数×每个饼要烙的面数÷一个锅最多放的饼数。
师:观察表6,烙饼所需的最少时间和什么有关?它们有怎样的关系?
生4:烙饼所需最少时间=烙1面饼的用时×烙饼次数。
师:这个公式适用于所有情况吗?
生 5:不适合1张饼的情况,因为1张饼的两面不能同时烙。
生 6:如果一次能烙3张饼,每个饼烙的面数就不能和每次最多放的饼数相抵消了,所以这个公式只适合一次放2张饼的情况。
【教学思考】通过观察烙饼时间分析表,很多学生都能发现“烙的次数等于饼的张数”这一规律,但并不理解其背后的真正原因。而通过质疑公式的局限性,能让学生理解公式背后的真正含义,从而提升思维的严谨性。烙饼问题这节课通过一系列的观察、操作、归纳、总结、转化,将学生的思维以一个动态发展的过程呈现,让思维得以提升、发展。
综上所述,图示在烙饼问题中起着重要的作用,它通过可视化的方式展示烙饼的初始状态和每次操作后的位置變化,帮助学生直观地观察和分析问题。通过图示,学生也更清楚地理解烙饼的顺序和位置关系,发现规律和性质,从而制定最优的解题策略。在教学中,教师要善于借助图示解决教学中的难点,让学生的思维真正做到动态化。
[ 参 考 文 献 ]
[1] 李小燕.借助图示直观突破教学重难点[J].广西教育,2019(21):93-94.
[2] 沈强.借助多元比较,深化概念理解[J].小学数学(数学版),2022(5):72-73.
[3] 侯小卿.巧用图示表征促进小学数学学习[J].考试周刊,2018(6):65-66.
(责编 覃小慧)
