圆盘形结构的非接触式电压传感器设计与实验
2023-12-25李远李孟阳杨家全梁俊宇袁兴宇汪金刚
李远,李孟阳,杨家全,梁俊宇,袁兴宇,汪金刚
(1. 云南电网有限责任公司电力科学研究院,昆明 650217;2.输变电装备技术全国重点实验室( 重庆大学电气工程学院) ,重庆 400044)
0 引言
近年来,随着我国输配电技术的不断发展,电力系统运行的可视化、数字化已经成为时代要求[1-3]。其中电网中电压的实时测量对于全面获取电力系统的运行状态具有极其重大的意义,可有效提高电网运行的效率以及安全性[4-7],为此,大量的学者对电网电压测量进行了研究。
电网对于电压监测的选择以传统的接触式分压系统为主[8-10],这种电压的监测方式可靠性较高,但是存在价格昂贵、安装和维修困难等缺点,使其无法满足现在的电力系统监测需求[11-13],如工频测量和暂态测量能力较好的电容式电压互感器( CVT) 因其体积庞大,需要与线路直接接触等原因,无法对其进行广泛的部署[14-15]。为提高电压测量的便利性,有些学者提出了非接触式电压测量系统,它具有与主要设备无电气连接、无需为传感器提供额外电源、宽频带和快速响应的特点[16-17]。然而,非接触式电压传感器测量电压时需要测量三相电压,测量过程中会由于电场耦合,导致结果稳定性和准确性不高[18-19]。且在实际的运行过程中,极易受到外界因素的干扰,如天气、人为的误差等[20-21]。
球形传感器结构在矢量电场中因为其结构特性可进行有效的电压测量[22],但在实际工程运用中由于竖直方向上的电荷量难以完整检测,传感器测量范围无法覆盖全部电荷,得到的电压结果精度不高,且传感器空间的浪费较大。文章提出了一种非接触式的圆盘形电压传感器,该传感器调整了各个方向上的极板测量面积,优化了结构,增加了竖直方向上的矢量采集与分析能力,增强了解耦能力,从而对矢量电场信号测量的实时性、准确性和稳定性进行了提升。
1 传感器测量原理
1.1 电场耦合测电压原理
电压传感器在电场中如何得到电场信号的矢量特性,是电压测量的关键所在。以输电架空导线中的单导体电场与电势的耦合感应为例,如图1 所示。
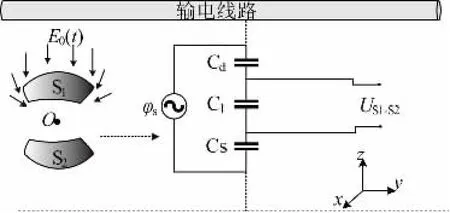
图1 单维弧面电极空间电场耦合Fig.1 Space E-field coupling of single-dimensional arc electrode
非均匀电场E的计算公式为:
式中E(r)为矢量电场信号;φ(s)为源电势;er为电荷指向测点的单位矢量电场方向;l为测点与导线的轴心中心距离;a为单源导体半径。由式( 1) 和图1 可知,使用单极板电场传感器对电场信号进行测量时,仅能得到电场信号的大小,而无法得到其方向,同样,若输电线路为三相导线,也无法得到准确的电场信号。增加传感器的矢量信号采集与分析能力,对于电压的测量至关重要。
1.2 电场信号矢量特性分析
在图1 传感器O 点处构建ex=(1,0,0) ,ey=(0,1,0) ,ez=(0,0,1) 三维正交基,可以得到空间电场矢量信号的划分,该正交基满足以下条件:
分别用Es1-s2、Es3-s4、Es5-s6代表z、x、y轴上的电场信号。当电压传感器位于输电线路下方测量时,由于地面的存在,输电线路的电场会在竖直方向上感应到地面上的电荷,因此产生了垂直于输电线路的电场信号,相比之下,在水平方向上的电场信号通常会较小,因为电流主要在输电线路的水平方向上流动,对水平方向上的电场信号的影响相对较小。
即Es3-s4<Es1-s2、Es5-s6<Es1-s2,在输配电线路中竖直方向上的矢量电场信号强于水平方向,测量难度更高。为得到完整的电场信号,需增大电场传感器竖直方向上的极板测量面积。该传感器结构对位极板的组合采用内接长方体切割所形成的对称弧面,具体表现为圆盘形结构。
2 圆盘形传感器分析
2.1 基于圆盘形结构测量电压原理
在圆盘形传感器的设计中,需满足单个极板可以完整的采集到对应方位上的电场分量,多维矢量感应模块可以实现空间电场的全覆盖感应,实现矢量信号的同步采集与合成的条件,且具备一定的抗角度偏差测量特性,如图2 所示。

图2 圆盘形传感器结构Fig.2 Disc-shaped sensor structure
分别用S1~S2、S3~S4、S5~S6表示该传感器在z、x、y轴上的极板,其结构参数如式(3) 所示:
式(4) 给出了圆盘形传感器对于电场测量的计算机制,可通过测量各个方向上的电场信号的大小,来准确的计算出电场信号的大小和方向。若在测量过程中,传感器发生了一定的偏移,如图3 所示。
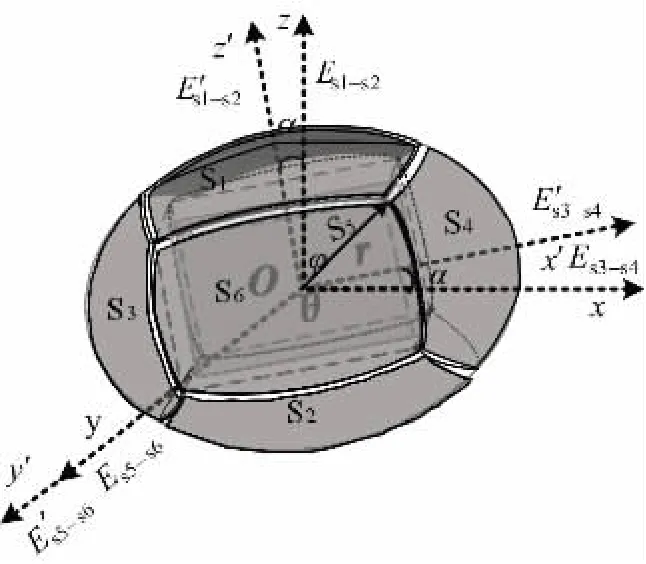
图3 传感器角度偏移Fig.3 Sensor angle offset
传感器在x-z平面上偏移角度α,此时y轴的位置不会改变,则各个方向上的电场信号变化为:
式(5) 表明由于圆盘形传感器结构的特点,在进行电压测量时,即使传感器发生一定的偏移,电场信号的输出信号幅值不会发生变化。说明圆盘型传感器具有抗角度干扰的能力,满足准确测量电场信号的设计要求。
2.2 圆盘形传感器等效电路分析
建立圆盘形传感器的综合等效电路模型,需要考虑到含对位、间位、邻位的对应分布电容以及杂散电容。电容的大小只与导体之间的形状、尺寸、相互位置以及导体间的介质有关,与带电的实际情况无关,而由于圆盘形传感器水平方向上的对称性,电容的大小也具有对称的特点,如图4 所示。

图4 等效电路模型Fig.4 Equivalent circuit model
式(6) 中,Hx、Hy、Hz为传感器的差动输出矩阵函数项,表示电压与电场之间的线性比例关系,其大小由仅由电路中的电容、电阻有关。通过节点电压方程,便可得到H值。
在图4 中,Is(s) =0,则可以将式(7) 化简为式(8) :
将图4 简化为节点模型,可得节点连通图,如图5所示。

图5 节点连通图Fig.5 Node-connected graph
根据连通图可得到关联矩阵A,基本环路矩阵Bf,旁路导纳矩阵Yb(s) ,进而推出式(9) :
因传感器与地面之间的距离较大,电容值的大小和两个导体之间距离成反比,故Csi和Cdi的数量级相较于输入电阻R 足够小,且因为水平结构的对称结构,C3与C4大小近似,则输出传递函数可以简化为:
图4 中,节点0 ~6 分别表示输电线路源等效电位和六个极点等效电位。C1为节点1 和节点2 之间的自电容,C2为节点1、2 与节点3 ~6 之间的互电容,C3为节点3 和节点4、节点5 和节点6 之间的自电容,C4为水平方向上邻位的互电容,Cd1~Cd6为极板与电势源导体之间的分布电容,Cs1~Cs6为极板与地面之间形成的杂散电容。
构建圆盘形传感器矢量电场信号输出矩阵:
其中幅频特性可表示为:
相频特性可表示为:
综上所述,教师应该以学生为中心,优化教学内容,改进教学方法,丰富教学手段,完善考核机制就能有效激发出学生热情,提高学生的工程实践能力,使学生更好地适应社会对电子技术人才的要求,提高他们的就业竞争力。
由于极板与地和激励源之间的距离远大于极板之间的距离,故自电容与互电容的大小远大于分布电容与杂散电容的大小。则Hz可近似为仅由R1、Cd1、Cd2、C1~C3的大小决定,同理,Hx和Hy可通过调节这些系数的大小,来改善圆盘形传感器的测量带宽、精度。
2.3 圆盘形传感器自解耦电压测量方法
受电磁场离散特性影响,传统电场传感器或互感器无法完全感知各个方向的电场信号,从而未能准确反映出真实电场情况,而三维电场传感器结构可采用自解耦型解耦方法来获得实际电场信号。文章所设计的圆盘形电场传感器便可通过自解耦技术获取准确的电场信号。在此过程中,电场与电势呈现的关系为:
式中,kAz~kCz、kAx~kCx、kAy~kCy分别为各组对位电极的方向分量系数矩阵,如kAz为A 相输电线路在z方向上对于电场信号的贡献,φA~φC则为三相电压。式(13) 的矩阵展示了圆盘形传感器和三相架空线路之间的三维电场信号的关系。可以得知,该解耦方法无需使用多个传感器,便可以准确地测量出三相互相作用的电场信号。
由高斯定理可知,传感器中心的电场强度E0为:
式中σ 为三相导线的组合虚拟表面电荷强度;r为测点与导线之间的距离;s则表示高斯积分曲面。对各组极板中心路径上的电场信号进行积分,得到每组极板的输出电压信号为:
其中gi为各组电极的中心距离,且g2=g3。uz、ux、uy分别表示三维感应电压信号。由电场高斯定理可知,若使用电场耦合式传感器测量电压,则:
式中V0为输出电压,正比于电场幅值与时间的一阶微分; εr为相对介电常数;Zm为该传感器的输出阻抗。根据式(16) 、式(17) 及σ∝φ,可得解耦系数为:
式(18) 中,λi为校对系数,与电极板厚度、所处位置等参数有关,若测点位置被确定下来,则λi可经过多次校准得到。在线路中的电压测量通过自解耦方法可以减少传统解耦方法所需要的传感器数量,且可设置位置参数来调整自适应矩阵系数。仅需一个圆盘型传感器便可得到三相电压信息,大大降低了解耦的难度,增强了电压测量的准确性与完整性,符合电场矢量信号测量的设计要求。
图6 中,d和R分别表示了导线间的间距以及导线的半径,h则为输电线路与地面之间的距离,rA、rB、C分别表示了测点与三条线路之间的距离。
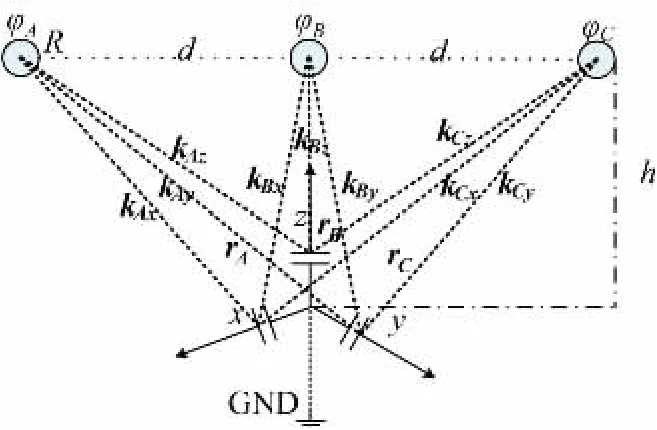
图6 自解耦方法示意图Fig.6 Schematic diagram of self-decoupling method
由于测点高度对称分布,解耦矩阵中的部分系数可相等。采用如下等效:kAx=kCyk1,kAz=kCz=k2,kAy=kCx=k3,kBx=kBy=k4,kBz=k5。由于该分量系数矩阵是非奇异矩阵,可将解耦矩阵化简为逆矩阵K-1的形式,得到:
3 仿真分析
为检验圆盘形传感器在电压测量中的实时性、准确性和抗干扰能力,建立如图7 所示的三维Maxwell 电场仿真模型。该模型以三相水平架空线为激励源、圆盘形传感器为观测目标,其导线参数、传感器参数、激励输入参数、边界条件等设置如表1 所示
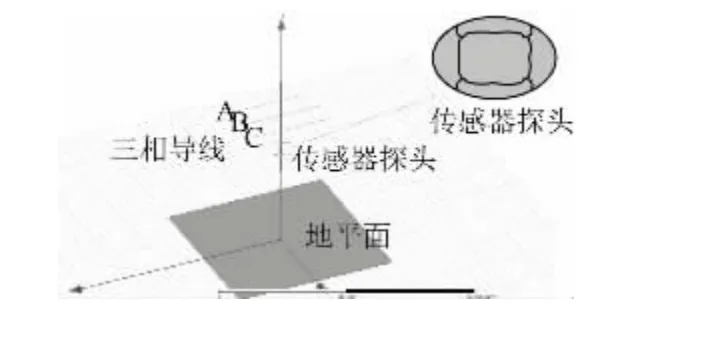
图7 三维Maxwell 电场仿真模型Fig.73D Maxwell E-field simulation model
为满足传感器圆盘形结构,在直角坐标系中引入一个半轴分别为a、b、c的圆盘形传感器结构,其参数关系为:
传感器的参数设为a=b=20 mm,c=10 mm。将传感器布置于中心水平线下方的[1.6 m,3.15 m]的高度位置,通过有限元仿真,可以得到传感器在各个时刻电场分布、极性、大小的变化情况。单周期内各个方向上的极板电荷量变化曲线如图8 所示。

图8 单周期内各个方向电荷量变化曲线Fig.8 Charge variation curve of each direction in a single period
ΔQ1-2、ΔQ3-4、ΔQ5-6分别代表z、x、y方向上单周期内的电场变化趋势,可以得到,当圆盘形传感器在激励源正下方测量电压时,各个维度感应的电荷量以及输出信号随周期变化,且与施加激励的变化周期一致,峰值、波谷以及过零点时刻都一一对应。极板信号输出幅度同增同减,不存在相差,具有良好的跟随性。且z轴上的电荷量明显大于x轴和y轴上的电荷量,需要更强的测量能力,说明了增大竖直方向上的极板测量面积符合提升测量准确性的设计要求。
为测量圆盘形传感器抗角度干扰能力,将该传感器以x-z进行平面进行偏移,即调整α 角,观测对位极板电荷量ΔQ在传感器偏移角从0 ~45°的变化,如图9所示。
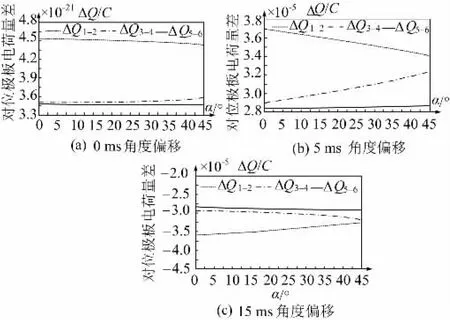
图9 不同时刻角度偏移所对应的极板感应电荷量差Fig.9 Difference in the amount of induced charge on the plate corresponding to the angular offset at different times
可以得到,圆盘形传感器可以测量出在各个时刻对应极板之间的电荷差因角度偏移而产生变化的值。在偏移角度大于15°时,电荷差变化尤为明显,但最终的E'幅值与偏移前的E幅值相差较小,可忽略不计。这表明该传感器对于角度偏移具有较强的抗干扰测量能力,符合电压传感器设计要求。
4 圆盘形传感器系统设计
4.1 硬件模块
为实现复杂空间电场信号的采集、处理、通信等功能,对圆盘形传感器进行针对性设计,其整体框架如图10 所示。
图10所示硬件处理电路主要由矢量电场感应探头、信号采集模块、中央处理模块、通信模块和显示平台模块组成。由信号采集模块实现三通道矢量电场信号的同步采集、触发采样功能; 中央处理模块以MSP430 系列的单片机为处理核心,实现信号处理、控制、低功耗模式等功能; 通信模块实现数据的快速传输,最终在显示平台显示。该电路满足圆盘形传感器测量的高精度、低功耗、信号采集与处理的设计需求。
4.2 系统程序
匹配相对应的硬件程序和上位机程序来实现硬件系统的协调工作。结合Quartus II、NI LabVIEW 操作平台,完成FPGA 软件端设计、上位机解析软件设计,以满足稳态/暂态电场测试数据的需要。总体系统程序逻辑如图11 所示。
在该框架中,FPGA 端软件负责数据采集、存储和读取以及通信功能,微处理器软件则实现了信号采样、无线通信、触发电平感知等功能。
5 电压测量实验
为检测圆盘形传感器对于电压的实际测量能否达到实时性、精确性且具有抗干扰能力的设计要求,搭建电场传感器测试平台。在该实验平台中,使用三相输电线路模拟激励源,三根输电导线的间距为0.6 m; 设置三相调压器,实现0 -20 kV/Hz 的分阶电压调节;增加冲击浪涌发生器,完成0 -12 kV/( 1.2/50 μs) 的分阶电压调节;增添高压探头Tek P50,在测量中得到的衰减比为1000∶1; 使用SMA 同轴电缆作为各个极板的连接线,可以消除其他信号对测量结果的干扰。实验平台具体布局如图12 所示。

图12 实验平台与现场测试图Fig.12 Experimental platform and on-site test diagram
为检验该圆盘形传感器电压测量的实时性、精确性和抗干扰能力,分别对其进行稳态测试、暂态测试和抗角度偏差测试,获取传感器的输出特性,并进行分析。
5.1 稳态测试
调节三相调压器,向三相输电导线施加在0 -20 kV 的电压范围内变化的电压激励,使得圆盘形传感器可在各个电压等级下进行实验,以检测电源的输入输出与传感器三维电场之间的联系。
为验证该传感器在矢量电场中测量的准确性,分别将标准电场感应以及矢量电场感应探头作为信号的输入。记测得的总标量记号为Es,矢量信号幅值输出为Uv,并以Es、Uv之间的线性度作为电压传感器各方向分量的线性关系,经过实验后可以得到图13 所示结果,图13 表明了合成场强Es、电压Uv与激励电压UTek之间存在线性度。

图13 线性度测量结果Fig.13 Linearity measurement results
由图13 可以得到以下表达式:
式(20) 和式(21) 描绘了三维电场输出信号幅值、测点电场以及场源之间的关系。式(20) 和式(21) 系数常数项以及标准偏差单位均为km-1;截距表示电场,单位为V/m。图13 表明,在稳态测量时,竖直方向上的电压值更大,需要更大的极板测量面积。由式(20) 和式(21)可知,圆盘形传感器结构在进行电场测量时,无论各方向电场分量还是合成电场,均与场源具有较好的一致性响应关系,满足传感器测量的准确性要求。
5.2 暂态测试
为检验圆盘形传感器的暂态响应情况,通过冲击浪涌发生器对传感器施加1.2/50 μs 的电压波形,对其在高频情况时的信号测量跟随性能进行检验,在多段频率信号下进行测试的结果如图14 所示。
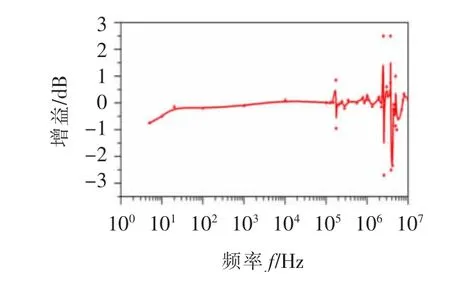
图14 高频动态响应图Fig.14 High-frequency dynamic response diagram
实验对不同频段的激励源进行了测试,从图14 高频测试结果可知,圆盘形传感器在各个频率段的放大增益系数均小于3 dB,保证了电压稳定测量时具有较大的带宽,但一旦频率高于兆赫兹,则该传感器的增益会出现较大的波动。说明圆盘形传感器可以在兆赫兹的频率范围内进行应用,实现电场信号的稳定测量。
5.3 抗角度偏差测试
将激励源的有效值固定在10 kV,对圆盘形传感器在正交坐标系上的法向位置进行调整,使其可以实现在x-z平面进行0° -45°的角度偏移,并测量其总体输出电场信号幅值,与标准电场测量仪进行比较,得到测量误差,每次角度变化测量五组,取平均值,最终得到结果如表2 所示。

表2 不同偏置角情况下传感器的响应特性Tab.2 Response characteristics of the sensor under the condition of various offset angle excitation
可以得到,当偏移角度为0°的时候,幅值测量所得误差较小,当偏移角度逐渐增加到15°,幅值偏移误差增加的较小,与仿真结果一致。而若偏移角度逐渐大于15°时,幅值的测量误差较大,但在实际工程应用中,若角度偏移大于15°时,圆盘形传感器偏移已经较为明显,需要直接进行调整。这表明,即使圆盘形传感器在测量电压发生角度偏差,依然能够充分感应到来自三维方向上的电场分量,该电场传感器具有较为稳定的电场幅值测量效果和抗角度偏差测量能力。
6 结束语
基于矢量电场中电压传感器测量困难的问题,设计了一种基于圆盘形结构的非接触式电压传感器,对圆盘形传感器的结构与测量原理进行了分析; 建立了以三相架空线路为激励源的有限元模型,对该传感器进行了仿真分析;并搭建了现场实验平台,进行了稳态实验、暂态实验和抗角度偏差测量。得到以下结论:
1) 圆盘形传感器可以有效地测量矢量电场中的信号,得到其大小和方向,且因为其结构特点,有利利用了极板空间,完整地测量竖直方向上的电场信号。通过调节极板的自电容、互电容来改善圆盘形传感器的测量带宽、精度。提出一种基于测点场源结构参数的自解耦电压还原方法,实现了单传感器对三相电压的准确还原;
2) 仿真实验中,通过测量在一个周期内以及多个角度的圆盘形传感器电荷量差值,证实了水平方向上的电场分量小于竖直方向电场分量,极板信号输出幅度同增同减,不存在相差,具有良好的跟随性和角度抗干扰能力;
3) 电压测量实验中,稳态实验证明该传感器结构使得电场测量无论是各方向电场分量还是合成电场,均与场源具有较好的一致性响应关系,满足传感器测量要求。暂态实验证明,该圆盘形结构传感器在兆赫兹的范围内进行测量时,各个频率段的放大增益系数小于3 dB。且抗角度偏差实验说明圆盘形传感器在0° ~15°的偏移角度中测量误差较小,若偏移角度过大,可直接通过观察调整。
上诉实验表明,圆盘形传感器优化了结构,增强了传感器在竖直方向上矢量采集能力,满足电压传感器测量所需要的实时性、准确性和抗干扰能力。
