柔性互联配电网概率潮流算法研究

赵真，袁旭峰，艾小清，彭月，朱拉沙，朱江行

( 贵州大学电气工程学院，贵阳 550025)

0 引言

传统以辐射性架构运行为主的配电系统有着多回馈线负载不平衡［1］、供电可靠性差［2］等缺点。随着电力电子器件的快速发展，基于电压源换流器VSC( Voltage Source Converter) 的柔性直流配电技术得到快速发展，使中低压柔性互联配电成为可能［3］。柔性互联配电网有着闭环运行，分布式电源易于消纳，电能质量高等优点，已成为近些年研究热点。

随着能源革命的进行，以风光为代表的具有不确定性特征的分布式电源大规模接入柔性互联配电网已成为发展的必然趋势［4］。这种不确定性对柔性互联配电系统的可靠性［5］分析、经济规划、优化调度等研究带来巨大挑战。潮流计算是这些研究的基础，因此基于不确定性的概率潮流研究在新形势下显得愈发重要。概率潮流PLF( Probabilistic Load Flow) 计算方法分为模拟法［6］、点估计法PEM［7］( Point Estimation Method) 、解析法［8］三种。而现有的以上三种PLF 计算方法目前都是在交流配电系统层面实现应用，而对于以交替迭代算法为基础的柔性互联配电网概率潮流计算能否实现尚未有文献进行研究论述。

模拟法通常为蒙特卡洛模拟法MCS( Monte Carlo Simulation) ，是以大规模计算来准确求解PLF 的一种方法，但因为计算时间长往往作为其他方法有效性的对照方法，显然并不适合直接作为基于交替迭代法的柔性互联配电网概率潮流算法。解析法中常用方法是半不变量法，通常是将潮流方程线性化处理［9］得到输入变量与输出变量的线性关系进行求解，而柔性互联配电网交替迭代算法实则是交流潮流方程与直流潮流方程交替迭代计算的，对于这样两个系统潮流方程交替迭代形式传统半不变量法难以直接应用。点估计法是以确定性潮流计算作为基础，有着良好的计算速度与准确性，交替迭代法中间的耦合过程并不影响此方法的使用，因此针对目前尚未有柔性互联配电网概率潮流算法研究的现状，文中选择点估计法中准确度较高的三点估计法3PEM( Three-Point Estimation Method)作为实现方法。

1 柔性互联配电网拓扑结构

直流配电网通过电压源换流器连接多条交流馈线组成柔性互联配电网，柔性互联配电网有着潮流可控、电能质量高、分布式电源易消纳等优点，已成为未来配电网的主要发展方向。

文中提出基于三点估计法的柔性互联配电网概率潮流计算方法。以改进交替迭代算法作为确定性潮流算法; 以Nataf 变换方法结合Cholesky 分解进行风电、光伏不确定变量的相关性处理;最后以IEEE 33节点结合直流配电中心组成柔性互联配电网作为算例，验证所提算法的有效性，如图1 所示。

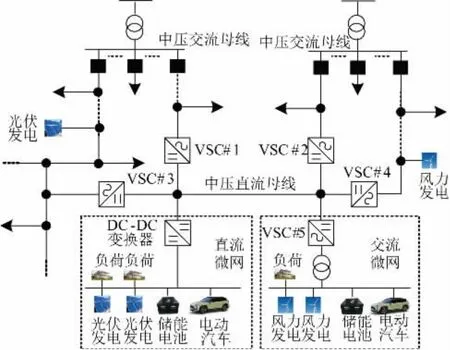
图1 柔性互联配电网拓扑图Fig.1 Topology of flexible interconnected distribution network

2 改进交替迭代算法

改进交替迭代算法相比传统的交直流交替迭代算法计算时间大大缩减。此方法对换流器端口潮流模型分界重新进行划分，将两个子系统( 交流子系统、直流子系统) 划分为三个子系统( 交流子系统、直流子系统、换流器系统) 更贴近于实际的运行情况。其改进后的等效示意图如图2 所示，其中PCC 表示交流网络，Ps、Qs分别为交流端的注入换流器有功、无功功率，Pc、Qc为换流器端注入直流电网有功、无功功率，Zc为换流器等效阻抗，Pdc、Qdc为直流电网电压与功率。

图2 VSC 稳态潮流模型Fig.2 VSC steady state power flow model

为了提高计算速度此方法将交替迭代过程划分为两个阶段进行处理，第一阶段为解耦处理即将流过换流器的损耗近似为1%( VSC) 或3%( 多电平换流器为) ，以式(1) 、式( 2) 分别得到定交流有功、定直流电压控制模式下的直流节点有功功率初值。在2 次～3次交替迭代后便可得第一阶段结果更加接近真实值。第二阶段将第一阶段得到的结果作为初值带入常规交直流迭代方程进行计算，在更少的迭代计算中得到最终结果，具体计算过程见文献［10］。

其中i与j表示直流系统节点号(i≠j) 。

3 输入变量概率模型

3.1 风电概率模型

风速的概率密度PDF( Probability Density Function) 服从Weibull 分布，表达式为:

式中v、k、c分别为风速以及形参与尺参。

有功功率函数表达式为:

式中Pwg、Pr分别为实际与额定功率;vin、vr、vout分别为最小、额定、最大风速。

3.2 光伏发电概率模型

光强的PDF 按Beta 分布，表达式为:

式中a、b 为形状参数;r为实时光强，rmax为光强最大值。则光伏发电输出功率Ps为:

式中A为总面积;h为转换效率。

3.3 负荷概率模型

负荷PDF 以normal 分布表示:

式中PL、QL表示有功与无功功率; μp、δp分别为有功期望与均方差; μQ、δQ分别为无功期望与均方差。

4 计及输入变量相关性的三点估计法

4.1 三点估计法

点估计法是一种通过近似计算得到输出变量数字特征的方法。设点估计法点个数为m，随着m的增多，近似得到的结果越接近真实值，但因为四阶以上中心矩难以求得，因此一般以两点估计法、三点估计法为主。而m=3 的三点估计法因为准确度更高，在概率潮流计算中应用更广泛。

设n维输入变量Xi的h维输出变量构成的多元函数为H=F(X) ，Xi的3 个点xi，k为:

式中μxi、σxi、ξxi，k分别为期望、标准差、位置系数。

点xi，k的权重系数pi，k为:

其中ξxi，k、pxi，k可由下式求得:

求得的位置与权重系数为:

求出ξxi，k、pxi，k后，由式(12) 可近似求得输出变量的各阶原点矩为:

4.2 输入变量相关性处理

三点估计法通常只能处理独立随机输入变量，但实际随机输入具有相关性，因此需要对相关性输入变量进行处理，以满足点估计法的要求。Nataf 变换是一种处理输入变量相关性的常用手段［11］。

设X为n维具有相关性的非正态输入变量，相关系数矩阵为CX，矩阵i行j列对应元素为ρij。设独立标准正态分布变量为Y，相关系数矩阵为CY，i行j列对应元素为ρoij。

X与Y之间的关系为:

式中Φ－1(·) 为标准正态分布逆累积分布函数;F(·) 为累积分布函数CDF( Cumulative Distribution Function) 。相关系数定义如下:

式中σi、σj为xi、xj的均方差。

ρij与ρoij之间满足:

由于式(15) 计算复杂，对于风电常用文献［12］中的经验公式进行计算，如式(16) 、式(17) 所示:

而对于光伏转化系数可用文献［13］中改进方法，以三阶多项式变换法代替，如式(18) 所示，式中a表示三阶多项式变换系数。

经上述变换求出CY后对其进行Cholesky 分解:

得到下三角矩阵L。经过Z=L－1Y 变换便可得到独立标准正态分布输入随机变量。

5 算法流程

改进交替迭代法潮流方程简化为:

式中R为输出向量。以三点估计概率潮流算法求出输出变量的各阶原点矩后，用Cornish-Fisher 级数［14］拟合得到输出变量的PDF 与CDF。

设α 为随机变量的z分位度，则z( α) 可表示为:

式中ξ( α)=Φ－1( α) 。

由z( α)= F－1( α) ，便可求得z的累积分布F(z) 。

算法流程如图3 所示。

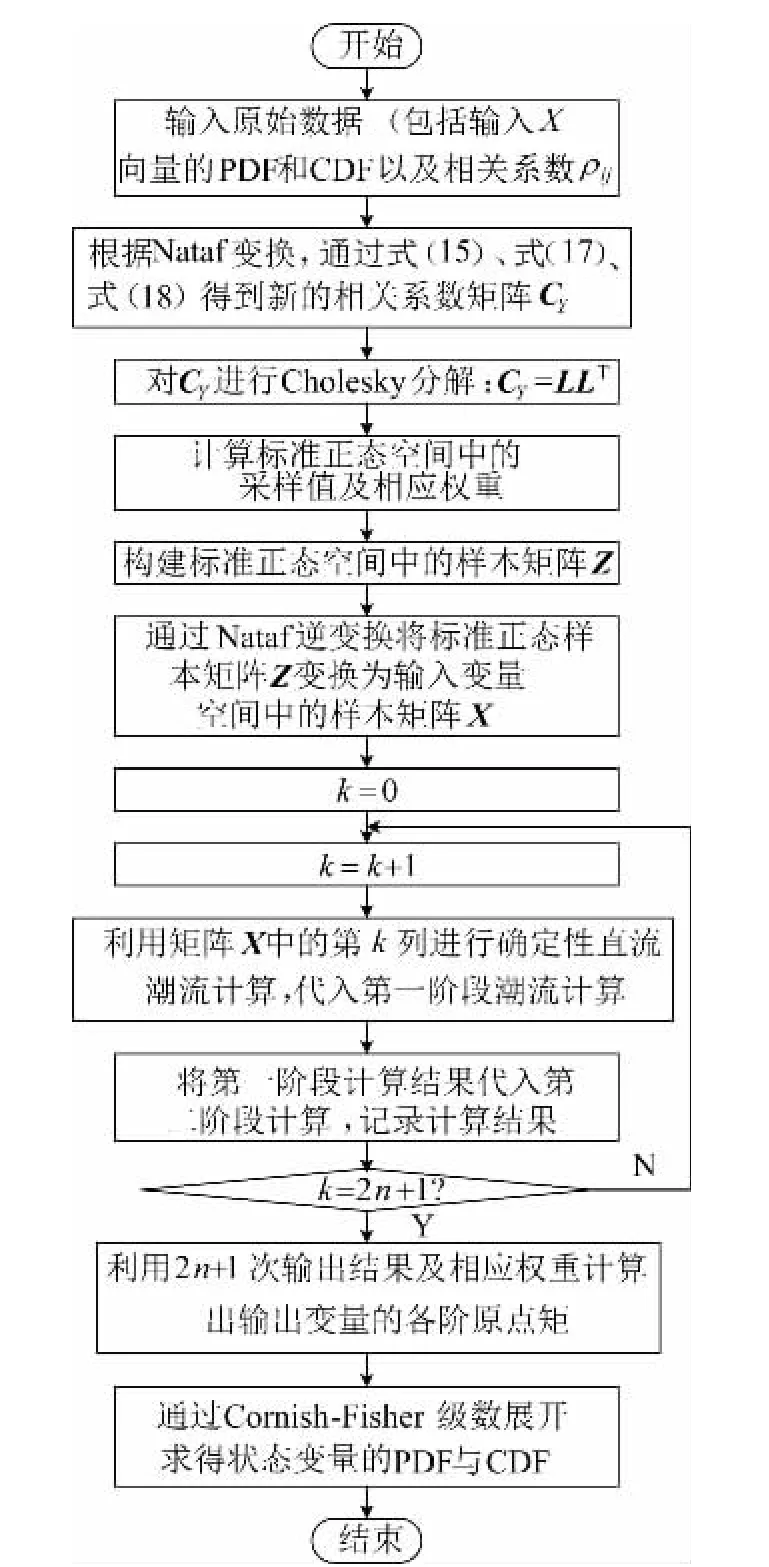
图3 算法计算流程Fig.3 Algorithm calculation process

6 算例分析

6.1 参数设定

以改进的IEEE 33 节点配电网结合国内首个五端柔性直流示范工程-直流配电中心组成柔性互联配电网作为算例进行验证，结构模型如图4 所示。

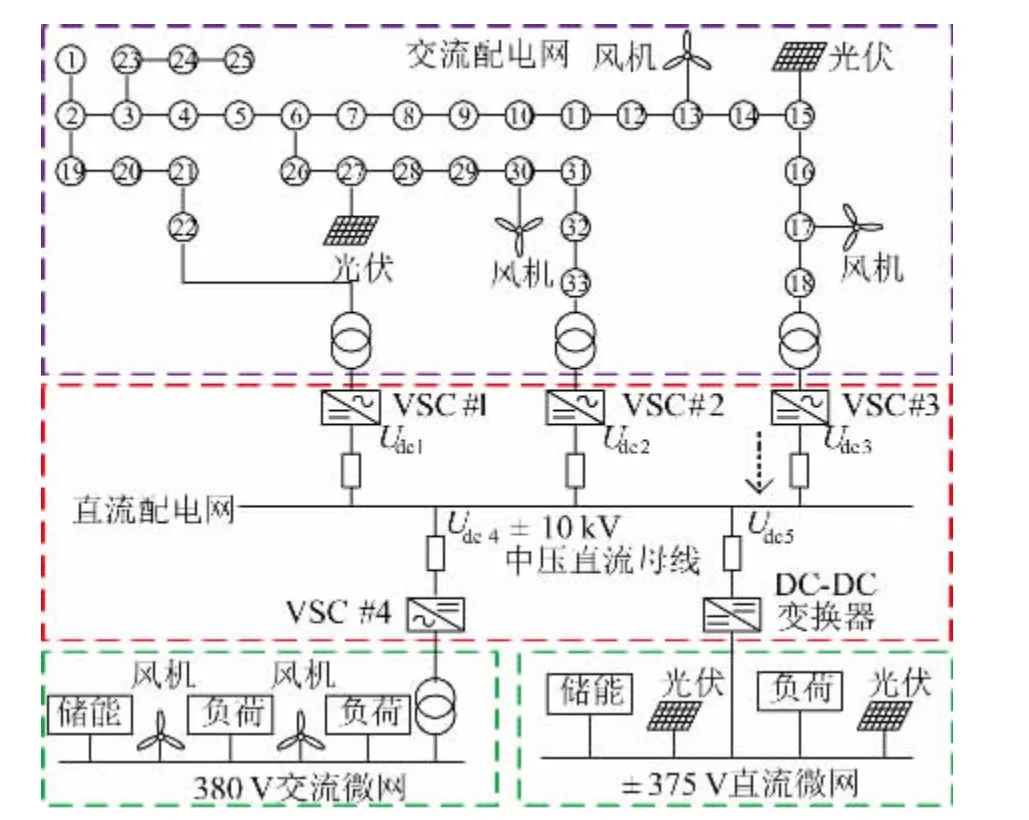
图4 柔性互联配电网算例图Fig.4 Calculation example of flexible interconnected distribution network

系统基准容量为10 MVA，交流网络基准电压12.66 kV，直流系统基准电压为10 kV，直流线路电阻均为0.005 p.u.。换流器具有相同参数: 电阻为0.02 p.u.，电导为0.033。交流网络中的13、17、30 节点接入装机容量分别为300 kW、400 kW、200 kW 的3 组风电机组; 直流网络中的交流微网接入2 组有功功率为300 kW 的风电机组。风电机组均服从形状参数为7.0，尺度参数为1.8，切入、额定、切除风速分别为4 m/s、15 m/s、25 m/s，功率因数为1 恒定运行。5 组风电机组间的相关系数矩阵如式(22) 所示。

在柔性系统中共接入4 组装机容量均为100 kW的光伏发电机组，分别接于交流网络中15 节点、27 节点以及直流网络的直流微网中。光伏机组服从形状参数分别为0.6798、1.7888，光电转化率0.13，最大光强1.1333 kW/m2，功率因数为1 恒定运行。相关系数矩阵如式(23) 所示。

在直流配电网的直流微网与交流微网各接入一组充放电功率为250 kW/h 的储能电池，以恒功率方式进行处理。对IEEE 33 节点系统进行简化处理，保持负荷有功不变，各节点负荷功率因数都为0.55 进行计算。同时直流网络中的交流微网与直流微网共接入3组有功功率均为200 kW 的负荷。柔性系统中负荷间相关系数均设定为0.4，变异系数( 标准差) 为0.1。

计算过程对两个微网进行等值处理为不含中间电压变换环节的电源或负荷( 等值电源指将同一微网中以文中方法得到的分布式电源的样本数值减去负荷的样本数值，等值负荷反之即可) 。图4 中Pdc1表示换流器1 注入有功功率功率，箭头方向表示注入功率的正方向。Udc1表示为节点1 直流电压。

为了验证文中算法的准确度，以MCS 计算结果作为比较值。以式( 25) 、式( 26) 的误差指标进行评价。其中μMCS、σMCS为MCS 的期望与均方差，μ3PEM、σ3PEM为3PEM 的期望与均方差，Nr为输出变量的维数。

6.2 场景一

储能电池切换至非工作模式，换流器组设定主从控制模式，即换流器1 为定交流有功/定交流无功模式(0．06/ －0．17，参数单位均为标幺值) ，换流器2 为定直流电压/交流无功模式(1/0．07) ，换流器3 设定为定交流有功/定交流电压模式( 0．03/0．97) ，其余电压初值均为1。以20 000 次MCS 计算所得结果作为精确值进行参考，表1 给出部分输出量平均相对误差( εμ－max、分别为期望最大误差与平均误差，εσ－max、分别为标准差最大误差与平均误差) ，交流系统电压幅值V、电压相角δ、线路有功功率Pij，直流系统电压Udc、换流器注入功率Pdc。

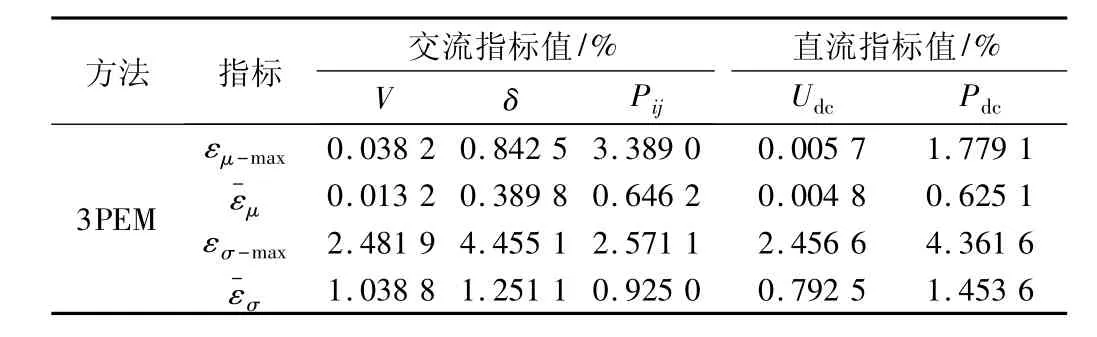
表1 场景一相对MCS 的误差指标Tab.1 Scenario 1 error index relative to MCS

由表1 可以看到，交流系统与直流系统部分输出变量的期望值与标准差平均相对误差都维持在1.5%以内，最大误差均在5%以内。同时，20000 次MCS 耗时27632.2035 s，三点估计法耗时48.6956 s，相比MCS 计算时间大大缩短。因此三点估计法在场景一下的柔性互联配电网概率潮流计算中保持良好的快速性与准确性。

图5 给出部分输出变量( 交流系统风电注入节点17 的电压幅值、风电注入的线路13-14 的有功功率、直流节点4 的电压幅值、换流器1 的注入直流有功功率)拟合得到的PDF。图5 中可以看到由3PEM 拟合得到的PDF 与MSC 图像基本保持一致。同时相对于交流节点电压幅值波动范围直流节点电压幅值的波动范围要小得多，展现出柔性直流配电网在接入分布式电源方面优异的性能。

图5 部分输出变量的PDFFig.5 PDF of partial output variables

6.3 场景二

储能电池切换到充电模式，换流器参数设定与场景一保持一致。与20000 次MCS 计算结果对比，部分输出变量相对误差如表2 所示。

由表2 得，各变量期望平均相对误差均小于0.7%，标准差平均相对误差均小于1.2%，期望最大误差均小于3%，标准差最大误差均小于4%，准确性良好。图6给出直流节点4 的电压PDF，与场景一直流节点4 的PDF 比较可以看出加入储能装置后，节点4 电压的波动范围更接近于额定值1，反映出储能良好的平抑功率波动保持电压稳定的能力。

6.4 场景三

换流器组设定为混合控制模式，即将换流器1 调整为直流电压下垂/交流无功控制模式，其初试运行点数据为下垂控制系数0.47、功率0.06 以及交流无功－0.17( 单位均为标幺值) 。其他参数与场景二保持一致，与20000 次MCS 比较后，相对误差如表3 所示。

由表3 可以看出，在混合控制策略下，误差指标依然处于适度范围内。综合场景一、场景二与场景三误差指标可看到3PEM 在不同换流器组控制策略下能够保持良好的准确度与快速性，适用于柔性互联配电网概率潮流计算。

7 结束语

文章针对目前鲜有柔性互联配电网概率潮流算法研究的现状，结合不同概率潮流算法的特点，提出基于三点估计法的柔性互联配电网概率潮流计算方法。以改进交替迭代算法作为柔性互联配电网确定性潮流算法，以Nataf 变换方法结合Cholesky 分解对风光负荷进行相关性处理。以IEEE 33 节点结合五端直流配电网-直流配电中心作为算例，分析了该方法的有效性。

与MCS 方法相比此方法在获得相似精度的情形下，大大降低计算所用时间，同时在换流器的主从控制策略与混合控制策略下该方法都能保持高效的计算速度与良好的精确性。