直驱风电场经交流并网系统dq 阻抗模型及稳定性分析

2023-12-25肖垒蔺红

电测与仪表 2023年12期

肖垒，蔺红

( 新疆大学电气工程学院，乌鲁木齐 830047)

0 引言

近年来，以光伏和风电为代表的新能源发电得到了快速发展和应用。其与传统发电机组有所区别，新能源发电机组多采用电力电子变流器接入电网，风电机组控制器与电网相互作用可能引发新的次同步振荡［1］( Subsynchronous Oscillation，SSO) 。

目前针对新能源并网稳定分析的主要研究多采用频域下的阻抗分析法。阻抗分析法需要先建立风电场并网系统的频域小信号阻抗模型，然后采用基于阻抗特性的频域稳定判据来对系统进行稳定性判定［1］。当前，对风电场进行小信号阻抗建模主要以选取坐标系的不同分为两种方式: 在dq 旋转坐标系中建模和在abc 三相坐标系下建立正负序模型。

三相( abc) 建模的正负序小信号阻抗模型采用了谐波线性化的建模方法，得到一维阻抗。文献［2-3］建立了风电机组的正负序阻抗模型，并采用基于阻抗特性的奈奎斯特( Nyquist) 判据来对系统稳定性进行分析。但，由于风电机组控制器中锁相环的动态特性、dq轴控制器结构以及参数不对称等因素的影响，正负序阻抗存在耦合［4］。并且因为耦合项的存在使得采用正负序阻抗模型分析系统稳定性的结果存在误差。

基于同步旋转坐标的dq 阻抗模型得到的为二维矩阵模型。其与三相阻抗模型区别处在于，dq 阻抗模型的二维矩阵非对角元素表现出了控制策略中存在的耦合问题，进而能够得到更准确的稳定性分析结果。文献［5-6］建立了逆变器在dq 坐标系下的阻抗模型，并基于广义的奈奎斯特判据研究了接入电网强弱、锁相环带宽等因素对并网系统稳定性的影响。文献［7］建立了双馈风电机组在dq 坐标系下的导纳模型，结合广义奈奎斯特判据分析了电流环、锁相环等因素对系统稳定性的影响。

文章在计及网侧变流器锁相环特性、内部电流环、直流电压环等控制环节，综合考虑交流动态响应和功率传输特性，推导了适用于次同步振荡研究的直驱风电场经交流并网系统dq 等效阻抗模型。并在PSCAD/EMTDC 软件环境中扫频验证了阻抗建模结果的正确性。采用一种系统阻抗矩阵行列式的稳定判据，研究了接入交流电网时直驱风电机组网侧变流器内部PI控制参数对并网系统稳定性的影响。

1 直驱风电场经交流并网系统的阻抗模型

图1 所示为直驱风电场经交流并网系统的结构示意图。将整个风电场聚合为一台直驱风电机组，风电场经过汇流变将电能汇集至PCC( Point of Common Coupling) 处与交流电网相连进行传输并网。

图1 直驱风电场经交流并网系统结构示意图Fig.1 Schematic diagram of the AC grid-connected system structure of a direct-drive wind farm

直驱风电场的全功率变流器由于其直流侧的电容解耦作用，可将风力机、直驱永磁发电机和机侧变流器等效为一个直流电流源［8］。在对并网系统进行等效简化之后，其阻抗建模的重点集中在网侧变流器( Grid-Side Converter，GSC) 和交流传输线路，如图2 所示。

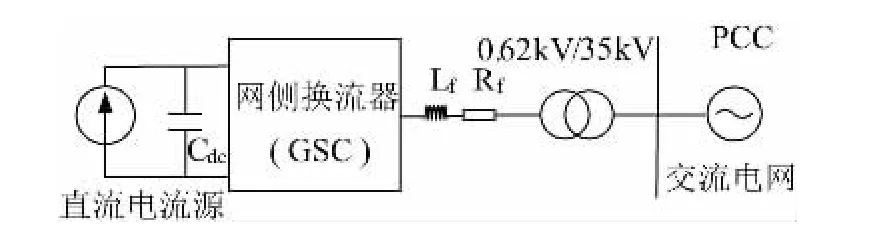
图2 直驱风电场经交流并网系统简化示意图Fig.2 Simplified schematic diagram of direct-drive wind farm via AC grid-connected system

1.1 直驱风电场阻抗模型

在建立网侧变流器的阻抗( 导纳) 模型时，选取频域内的电压/电流偏差ΔU、ΔI作为输入/输出，推导出输入/输出与控制策略实际变量之间的关系，得到呈现导纳( 阻抗) 特性的传递函数［9］。

永磁同步发电机发出的有功功率经背靠背换流器变频并网前，需要滤掉换流器产生的高频谐波，再经变压器提升电压等级后，经交流线路至PCC 点处。

直驱风电场网侧变流器的控制与响应如图3 所示，外环为电压环，内环为电流环［10］。

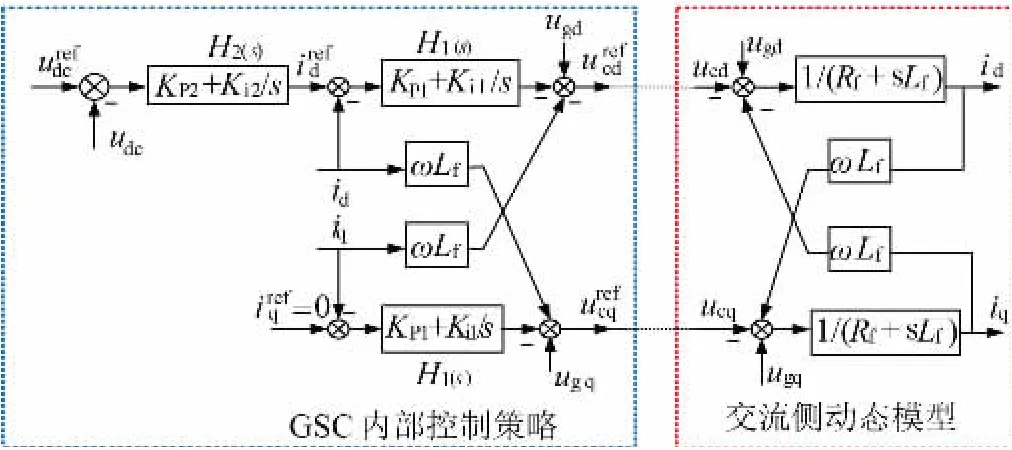
图3 GSC 的控制与响应框图Fig.3 GSC control and response block diagram

网侧变流器出口处电流电压在dq 同步旋转坐标下的频域动态方程为:

式中Rf、Lf为网侧变流器出口处滤波器的等效电阻以及电感。记(Rf+Lf) 为H0(s) ，为书写方便略去(s) 。

内环采用常规的解耦dq 电流矢量控制:

式中H1为内环PI 传递函数H1=。

风电机组变流器的开关频率高达数千赫兹，远远大于电源频率( 50 Hz) ，故在这样的开关频率下，变换器输出可以很快地跟踪其参考值［11］，即ucd/q= urefcd/q。联立式(1) 和式(2) 可得:

对式(3) 进行线性化得:

外环d 轴采用直流母线电压控制，同时能对有功功率进行控制:

H2为外环d 轴直流电压控制PI 传递函数H2=Kp2+。

网侧变流器的功率传输特征方程为:

式中Pw为风电机组输出功率，稳态时Pw= P0;Pg为注入PCC 处有功功率:Pg=(ugdigd+ ugqigq) 。

外环q 轴无功控制Q=0，此时变流器的功率因素为1，即=0 。

上述推导是基于变流器dq 同步旋转坐标系。由于锁相环环节的存在变流器dq 坐标与交流电网dq 坐标存在偏差。

锁相环( Phase-Locked Loop，PLL) 的输出是为了追踪电网电压的相位，其控制信号传递如图4 所示。

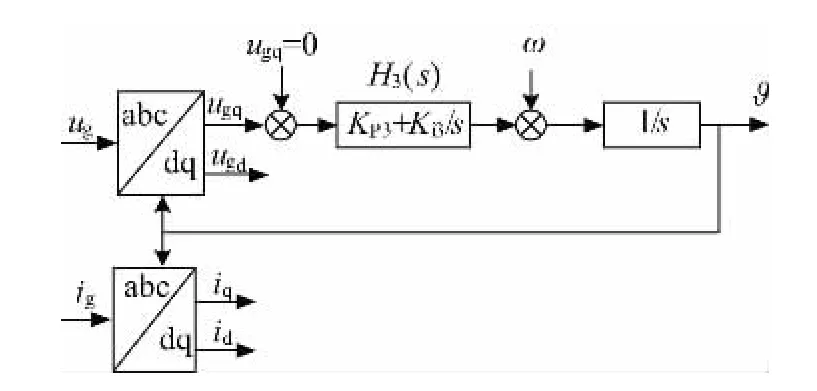
图4 锁相环( PLL) 控制框图Fig.4 Phase-locked loop ( PLL) control block diagram

在dq 坐标变换时，考虑锁相环动态的PPC 处电流电压与变流器出口电流电压之间的关系［12］如下:

式中H3为锁相环的PI 参数H3=;HP是锁相环闭环传递函数，;Δu、Δi为变流器出口处dq 坐标下的直流分量，Δug、Δig为电网PCC处dq 坐标下的直流分量。

结合式(3) 、式( 7) 和式( 8) 可得网侧变流器的阻抗模型，即直驱风电场的小信号阻抗模型可表示为:

1.2 交流线路dq 阻抗模型

交流线路dq 坐标下的阻抗模型［13］:

式中Rg、Lg为汇流变压器、线路的等效电阻以及电感; ω0为电网角频率。

1.3 风电机组交流并网系统dq 阻抗模型

由并网系统拓扑连接关系，可得系统dq 阻抗模型:

式中Zs为一个2 阶矩阵，表示直驱风电场经交流并网系统在dq 坐标系下的阻抗模型。

1.4 风电机组dq 阻抗模型验证

为验证所建并网系统dq 阻抗模型的准确性，在PSCAD 软件中根据表1 参数，建立仿真模型，采用扫频法［14］进行验证。

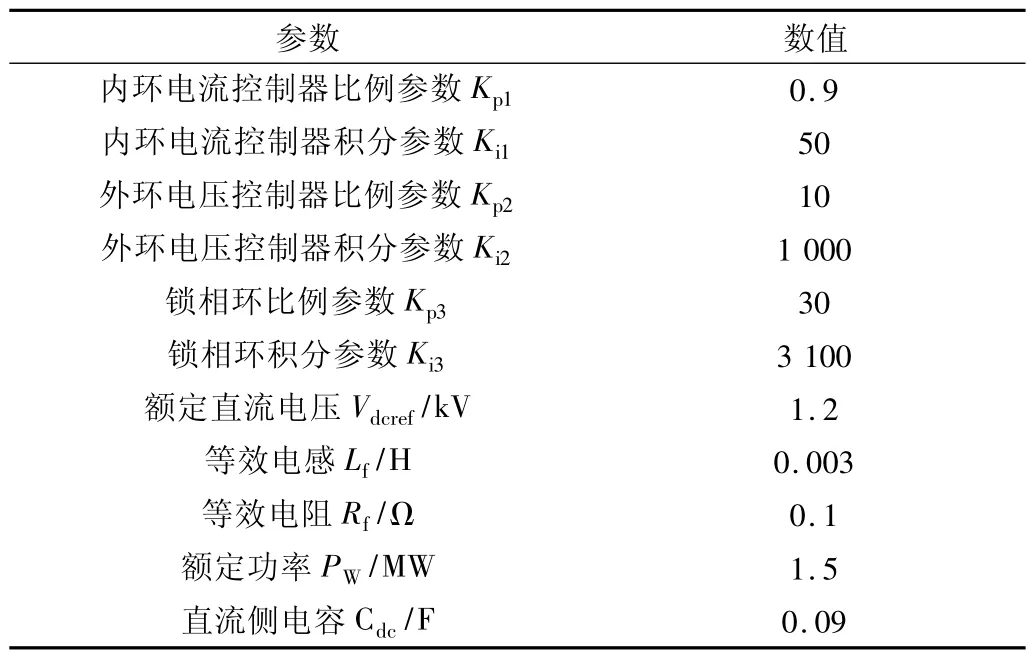
表1 直驱风电机组控制参数Tab.1 Direct-drive wind turbine control parameters

步骤分为:

(1) 向系统注入频率不同、幅值为5%的电压扰动;

(2) 测量网侧变换器在dq 坐标系下的电流响应;

(3) 对扰动电流和电压信号进行FFT 分析提取相应频率的幅值和相角，将其存储计算，进行Bode 图绘制。

直驱风电机组运行控制参数如表1 所示，将表1数据代入式(9) 即可获得风电机组在dq 坐标系下的阻抗解析曲线。

直驱式风电场连接弱交流系统时可能会出现次同步频率内的振荡风险，主要研究内容针对次同步振荡。次同步振荡频率范围内为2 Hz ～50 Hz［15］，考虑其频率耦合范围，故给出1 Hz ～100 Hz 范围内模型解析曲线与仿真扫频曲线，对所建立的模型进行验证，如图5 和图6 所示。

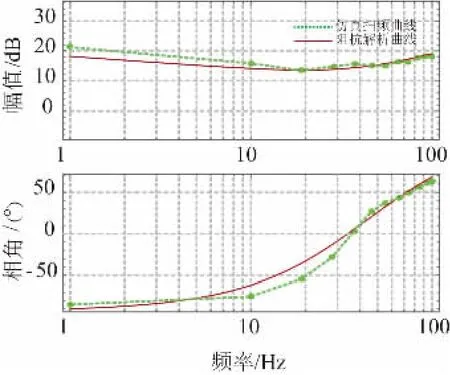
图5 Zdd阻抗模型解析曲线与仿真扫频曲线Fig.5 Zdd impedance model analytical curve and simulated frequency sweep curve

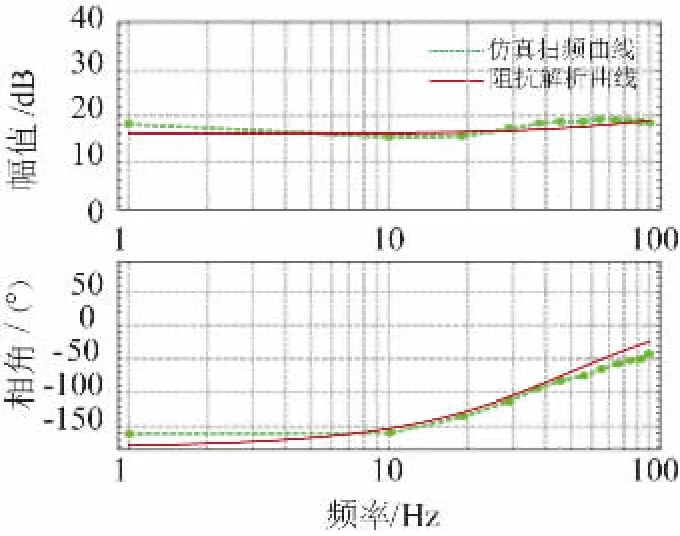
图6 Zqq阻抗模型解析曲线与仿真扫频曲线Fig.6 Zqqimpedance model analytical curve and simulation frequency sweep curve

经对比阻抗模型解析曲线和仿真扫频曲线，其具有良好的一致性，验证了所建立直驱风电机组dq 阻抗模型的正确性。

2 直驱风电机组控制参数对系统稳定性影响

直驱风电机组经交流并网系统中包含多个动态元件，系统阶数非常高，在实际应用中，Nyquist 稳定判据的条件过于苛刻，计算过程较复杂，许多学者为了便于电力系统分析的需要，推导出一些基于Nyquist 判据的衍生稳定判据。

2.1 基于dq 阻抗行列式的稳定判据

基于第一节中所建立的并网系统dq 阻抗模型Zs，对其行列式D( s) 进行分析，采用下述稳定判据［16］为:

(1) 当D(s) 虚频曲线从负向正穿越过零点时，如果Re［D( jωr) ］＞0，SSO 稳定;反之，SSO 不稳定;

(2) 当D(s) 虚频曲线从正向负穿越过零点时，如果Re［D( jωr) ］＞0，SSO 不稳定;反之，SSO 稳定。

其中ωr为D(s) 过零点频率。

2.2 电流内环控制参数对系统稳定性的影响

风电机组的阻抗特性与网侧控制器内部的参数有着密切的关系，从而会导致系统阻抗特性的不同。本文主要分析直驱风电机组控制器PI 参数对并网系统稳定性的影响。

2.2.1 电流内环比例参数对系统稳定性的影响

电流内环比例参数Kp1变化时阻抗行列式实频曲线与虚频曲线如图7 所示，当电流内环比例参数Kp1=1.08 时，虚频曲线由正向负过零点，虚部过零点频率12.5 Hz，对应频率处实频曲线值为－0.35 为负数，故SSO 稳定。

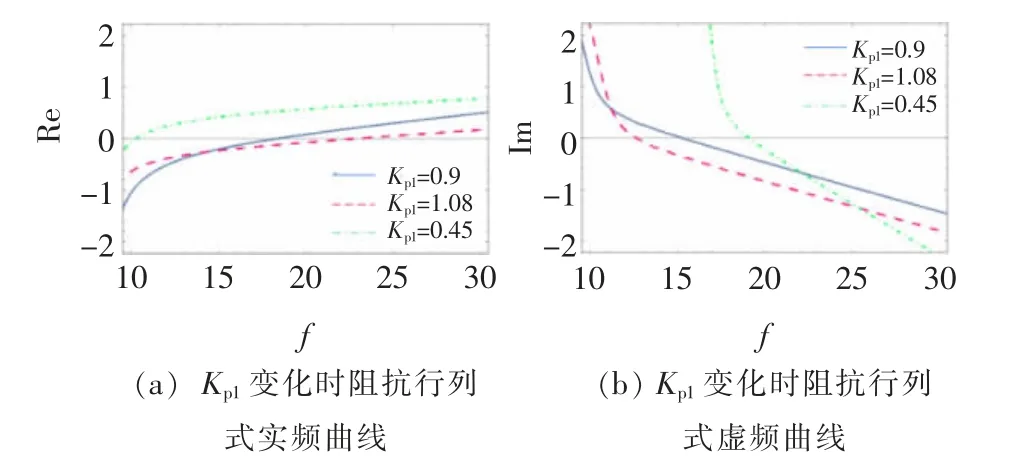
图7 Kp1变化时阻抗行列式实频曲线与虚频曲线Fig.7 Real frequency curve and imaginary frequency curve of impedance determinant when Kp1 changes

当电流内环比例参数Kp1=0.9 时，虚频曲线由正向负过零点，虚部过零点频率15.3 Hz，对应频率处实频曲线值为－0.17 为负数，故SSO 稳定。

当电流内环比例参数Kp1=0.45 时，虚频曲线由正向负过零点，虚部过零点频率19.1 Hz，对应频率处实频曲线值为0.54 为正数，SSO 不稳定。

对比电流内环PI 比例参数Kp1从1.08 减小至0.45，系统的状态由稳定到失稳，可知随着Kp1的减小，系统稳定性降低，发生振荡的风险升高，并且振荡频率变大。

2.2.2 电流内环积分参数对系统稳定性的影响

电流内环积分参数Ki1变化时阻抗行列式实频曲线与虚频曲线如图8 所示，当电流内环积分参数Ki1=75时，虚频曲线由正向负过零点，虚部过零点频率22.3 Hz，对应频率处实频曲线值为－0.34 为负数，SSO 稳定。

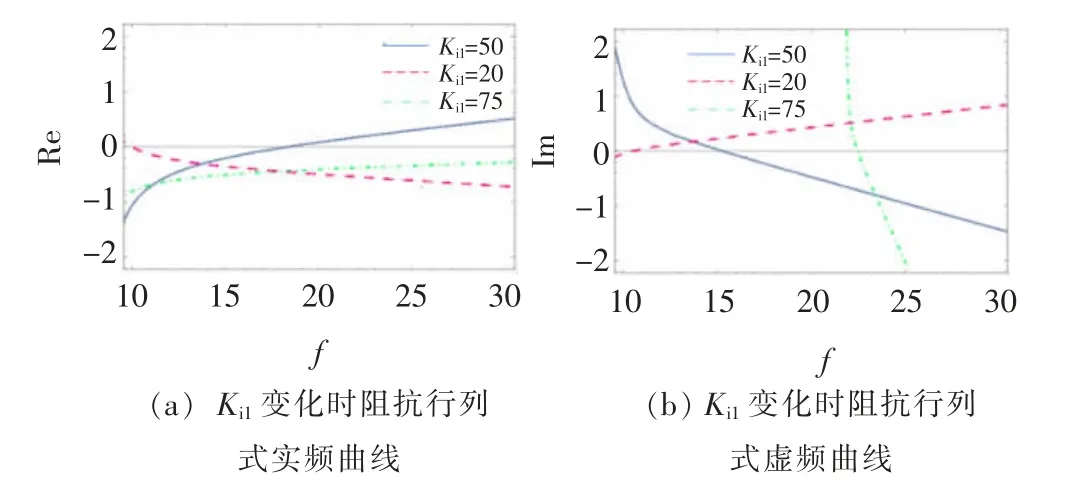
图8 Ki1变化时阻抗行列式实频曲线与虚频曲线Fig.8 Real frequency curve and imaginary frequency curve of impedance determinant when Ki1 changes

当电流内环积分参数Ki1=50 时，虚频曲线由正向负过零点，虚部过零点频率15.3 Hz，对应频率处实频曲线值为－0.17 为负数，SSO 稳定。

当电流内环积分参数Ki1=20 时，虚频曲线由负向正过零点，虚部过零点频率10.7 Hz，对应频率处实频曲线值为－0.11 为负数，SSO 不稳定。

对比电流内环PI 积分参数Ki1从75 减小至20，系统的状态由稳定到失稳，可知随着Ki1的减小，系统稳定性降低，发生振荡的风险升高，并且振荡频率变小。

2.3 直流电压外环控制参数对系统稳定性的影响

2.3.1 直流电压外环比例参数对系统稳定性的影响

直流电压外环比例参数Kp2变化时阻抗行列式实频曲线与虚频曲线如图9 所示，当直流电压环比例控制参数Kp2=15 时，虚频曲线由负向正过零点，虚部过零点频率11.4 Hz，对应频率处实频曲线值为0.86 为正数，SSO 稳定。

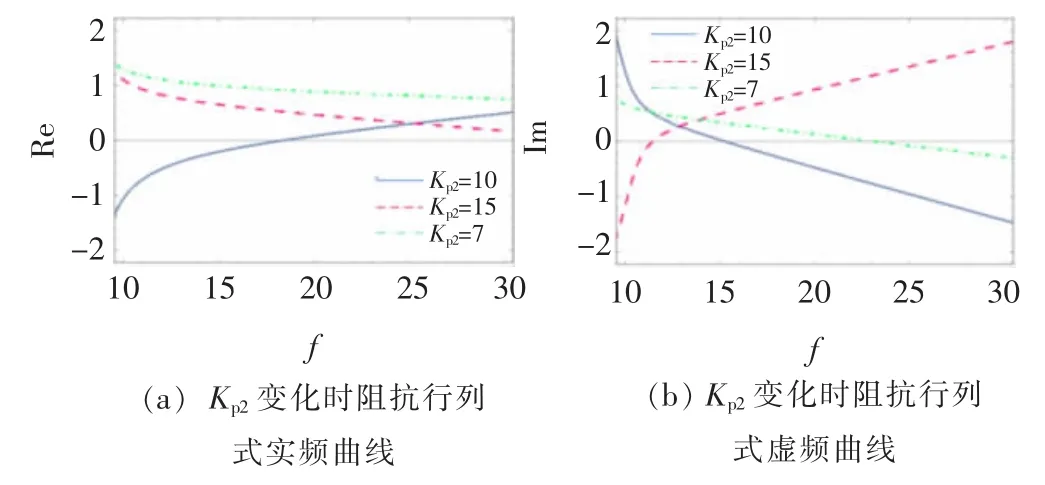
图9 Kp2变化时阻抗行列式实频曲线与虚频曲线Fig.9 Real frequency curve and imaginary frequency curve of impedance determinant when Kp2 changes

当直流电压环比例控制参数Kp2=10 时曲线由正向负过零点，虚部过零点频率15.3 Hz，对应频率处实频曲线值为－0.17 为负数，SSO 稳定。

当直流电压环比例控制参数Kp2=7 时曲线由正向负过零点，虚频曲线过零点频率23.3 Hz，对应频率处实频曲线值为0.82 为正数，SSO 不稳定。

对比直流电压外环PI 比例参数Kp2从15 减小至7，系统的状态由稳定到失稳，可知随着Kp2的减小，系统稳定性降低，发生振荡的风险升高，且振荡频率变大。

2.3.2 直流电压外环积分参数对系统稳定性的影响

直流电压外环积分参数Ki2变化时阻抗行列式实频曲线与虚频曲线如图10 所示，当直流电压环积分控制参数Ki2=1500 时曲线由负向正过零点，虚频曲线过零点频率24.4 Hz，对应频率处实频曲线值为0.19为正数，SSO 稳定。

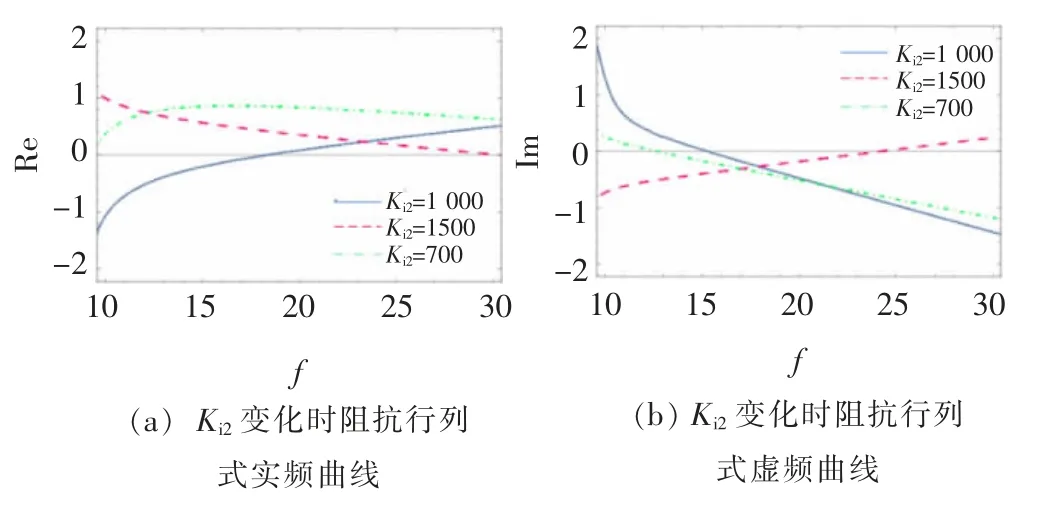
图10 Ki2变化时阻抗行列式实频曲线与虚频曲线Fig.10 Real frequency curve and imaginary frequency curve of impedance determinant when Ki2 changes

当直流电压环积分控制参数Ki2=1000 时曲线由正向负过零点，虚频曲线过零点频率15.3 Hz，对应频率处实频曲线值为－0.17 为负数，SSO 稳定。

当直流电压环积分控制参数Ki2=700 时，虚频曲线由正向负过零点，虚部过零点频率12.6 Hz，对应频率处实频曲线值为0.78 为正数，SSO 不稳定。

对比直流电压外环PI 积分参数Ki2从1500 减小至700，系统的状态由稳定到失稳，可知随着Ki2的减小，系统稳定性降低，发生振荡的风险升高，并且振荡频率变小。

3 直驱风电机组交流并网系统稳定性分析

在PSCAD 中建立直驱风电机组接入无穷大系统仿真模型，系统接线图如图1 所示，风电机组出力为1MW，变流器控制参数如表1 所示。由上一节分析，改变电流内环PI 比例参数Kp1=0.45 和电流内环PI 积分参数Ki1=20，其风电机组功率如图11 所示，分别对比Kp1=0.9、Ki1=50，皆发现其有功功率出现一定程度的振荡，明显地当Kp1=0. 45 时其振荡频率大于当Ki1=20 时的振荡频率，并且有功功率振幅也略高。可知电流内环控制参数中比例参数对稳定性影响较大。

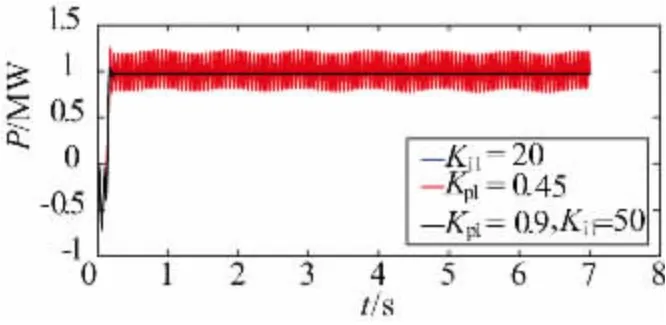
图11 内环控制参数( Kp1，、Ki1) 变化时功率图Fig.11 Power diagram when inner loop control parameters ( Kp1，Ki1) change

类似的，改变直流电压外环PI 比例参数Kp2=7 和直流电压外环PI 积分参数Ki2=700，其风电机组功率如图12 所示，分别对比Kp2=10、Ki2=1000，皆发现其有功功率出现一定程度的振荡，明显地当Kp2=7 时其振荡频率大于当Ki2=700 时的振荡频率，并且有功功率振幅也略高。可知直流电压外环控制参数中比例参数对稳定性影响较大。