基于自相关和时频分析的跳频参数估计*
2023-12-25解西坤
张 玮,王 平,解西坤,3
(1.海军工程大学 电子工程学院,武汉 430033;2.中国人民解放军92038部队,山东 青岛 266041;3.中国人民解放军91202部队,辽宁 葫芦岛 125000)
0 引 言
跳频[1-2](Frequency Hopping,FH)通信是最常用的扩频通信的方式之一,其信号的载波频率可随时间按伪随机规律跳变,具有较好的抗干扰、抗截获、抗多径能力,在军事和民用领域都有广泛的应用。获得准确的跳频信号参数是通信对抗领域的重要内容[3],因此,跳频参数估计逐渐成为信息对抗领域的热点问题。
目前跳频信号参数估计算法可主要分为时频分析法[4]和非时频分析法[5],而时频分析法是当前跳频信号分析的最常用的方法。时频分析法是通过时间和频率两个维度来描述能量密度变化的方法。文献 [6]提出了一种结合图像处理的跳频信号参数估计算法,采用一种迭代匹配算法抑制复杂的毛刺干扰信号。文献[7]提出了一种基于最大值的慢跳频信号检测算法,根据统计各信道辐射强度判断是否存在跳频信号。文献[8]以传统能量对消方法为基础进行改进,能够在完成信号检测的同时具有较好的鲁棒性和更小的计算量。但是,上述三种算法在低信噪比时性能较差。文献[9]提出了一种改进时频脊线的跳频参数估计算法,抗噪声性能较好。文献[10]提出了一种提出基于有噪模板的互相关监测方案,能够解决快跳频系统检测难算法性能低的问题。但是,上述两种算法在含有其他突发干扰时性能较差。文献[11]采用修正时频图和二次估计的方法实现跳频频率和跳变时刻的估计,具有较好的估计精度和抗噪声性能,但是仅能在高斯白噪声的条件下完成,存在其他干扰时算法性能下降较快。
为解决以上问题,本文提出一种基于自相关和时频分析的跳频参数估计算法。首先,通过基于能量检测的分段自相关算法对信号进行预处理预处理,利用短时傅里叶变换(Short-Time Fourier Transform,STFT)得到时频图像;然后,采用二值化和形态学滤波进行降噪提取;最后,通过聚类算法完成跳频信号参数估计。
1 跳频信号的数学模型
在观测时间T内接收到N个跳频簇,则跳频信号的数学模型可进行如下定义:
(1)
(2)
式中:rectTh为门函数;τ0为起跳时刻;Th为跳频周期;fk为第k个跳频簇的跳频频率;N是观察时间内频率跳变数量。
接收端信号r(t)中除了包含跳频信号s(t)外,还包括干扰信号J(t),可表示为
r(t)=s(t)+J(t)。
(3)
2 跳频信号特征参数估计方法
2.1 基于能量检测的分段自相关预处理
自相关是信号在不同时刻的数值相关性的一种描述,是信号时域处理的重要方法[12]。自相关函数定义如下:
(4)
式中:x(t)为待处理信号;τ为自相关函数的延时值;T为信号周期。
根据自相关函数的性质,随着延时τ的增加,高斯噪声的自相关值随之快速衰减,并逐渐趋近于零,而具有周期特性的信号自相关数值不会随着延时τ的增加而衰减,其周期特性会有效保留,因此可以采用自相关的方法对信号实施预处理,实现信号降噪。
跳频信号不是周期信号,但是其每一簇信号都是周期性的,因此需要对信号进行分段,算法的具体流程如下:
1)基于能量检测的时域分段
通过能量检测判断跳频信号数量,若已知跳频周期,时域分段的长度应与跳频周期长度相等,此时自相关运算效果最佳。在盲估计的情况下,设计一种时域分段算法,具体的执行流程如下:
输入:步长T0
输出:段长L
1 初始化i=1,从信号起点截取段长L=i×T0的信号x1(n),此时段长L=T0;
2 求取截取信号x1(n)的功率谱X1(m),求取X1(m)的最大值;
3 设置i=i+1;
4 重复步骤1~2,截取段长为L=i×T0的信号xi(n),计算截取信号功率谱Xi(m)的最大值;
5 判断Xi(m)的最大值是否继续升高,如果刚好不再升高,则输出此时的段长L=i×T0,如果最大值继续升高,则重复步骤4,直至最大值不再升高,然后输出此时的段长L=i×T0。
信号截取时刻的功率谱如图1和图2所示。观察图像可知,当截取信号长度为跳频周期时,功率谱图的最大值为第一簇跳频信号的频点,截取长度大于跳频周期时,第一簇信号频点的信号强度不再变化,而新截取的部分第二簇信号所在频点的信号强度随着截取长度变长而变大,因此当功率谱最大值不再发生变化时的信号长度即为时域分段的段长。
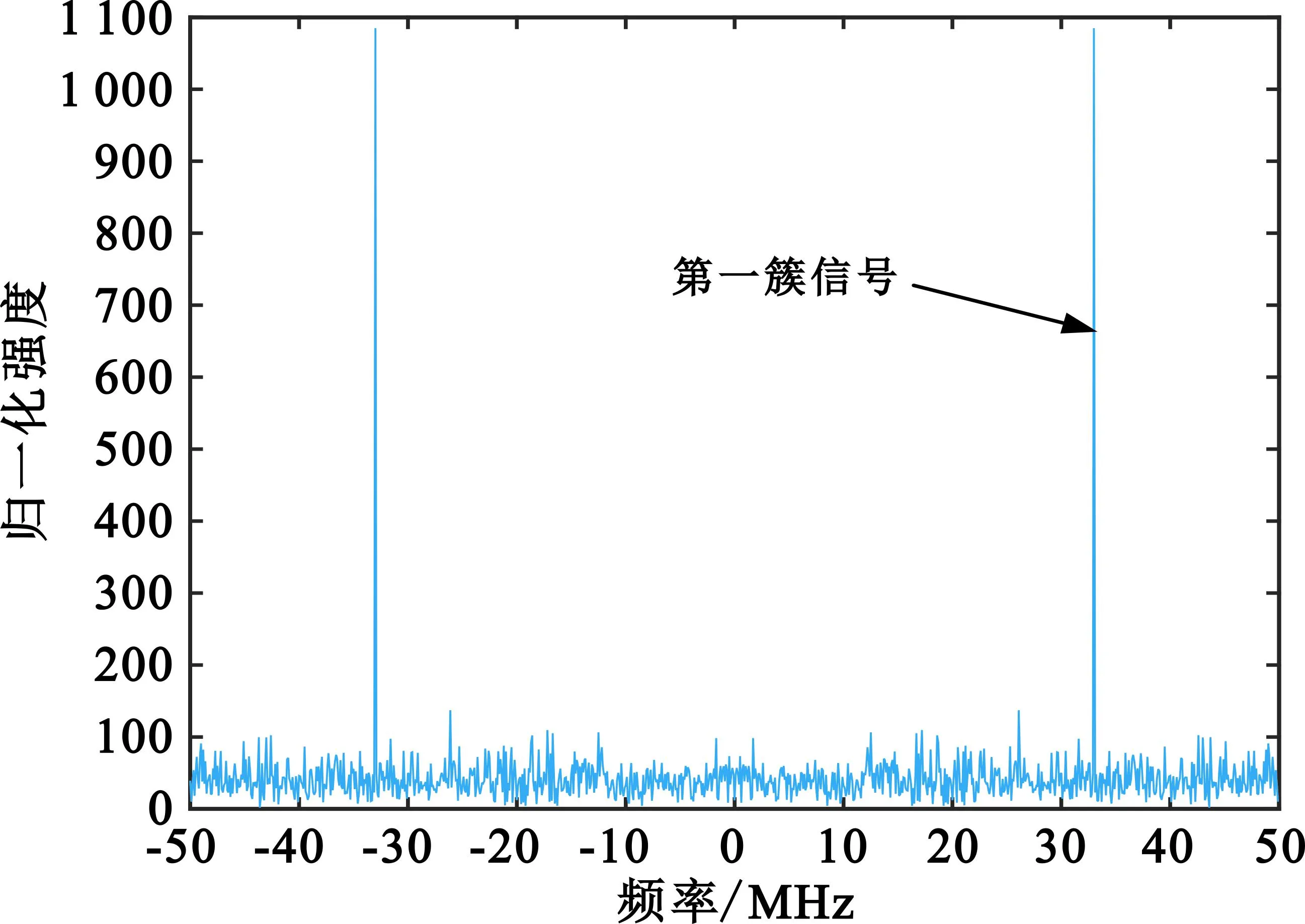
图1 第一簇信号功率谱
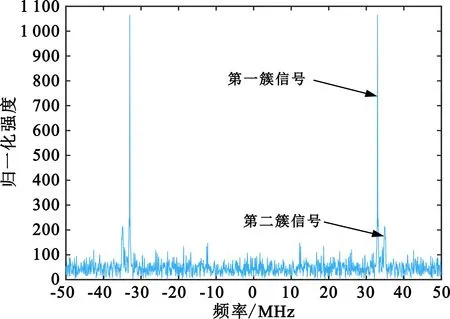
图2 过量截取信号功率谱
2)自相关运算
使用公式(4)对每一段信号进行自相关运算,得到每一段削弱噪声的时域信号。
3)信号拼接
将每一段信号拼接起来,可以得到完整的预处理信号。
因为短时傅里叶变换具有较好的时频聚集性,因此通过STFT的方式进行时频变换,可得到信号的时频图像。
图3为接收端信号未经预处理直接时频变换得到的时频图像,设置信噪比为-7 dB,图4为经过预处理降噪后的时频图像,可以看出经处理后消除了大部分高斯白噪声影响。在图4中可以看到竖直的细线形状的噪声,是因为当τ=0时噪声的自相关值最大,每两条细线的间隔为选取的步长,扫频信号具有周期特性,但是由于其周期大于步长,因此在一个步长内的扫频信号并无周期特征,自相关运算也消除了扫频信号带来的干扰。
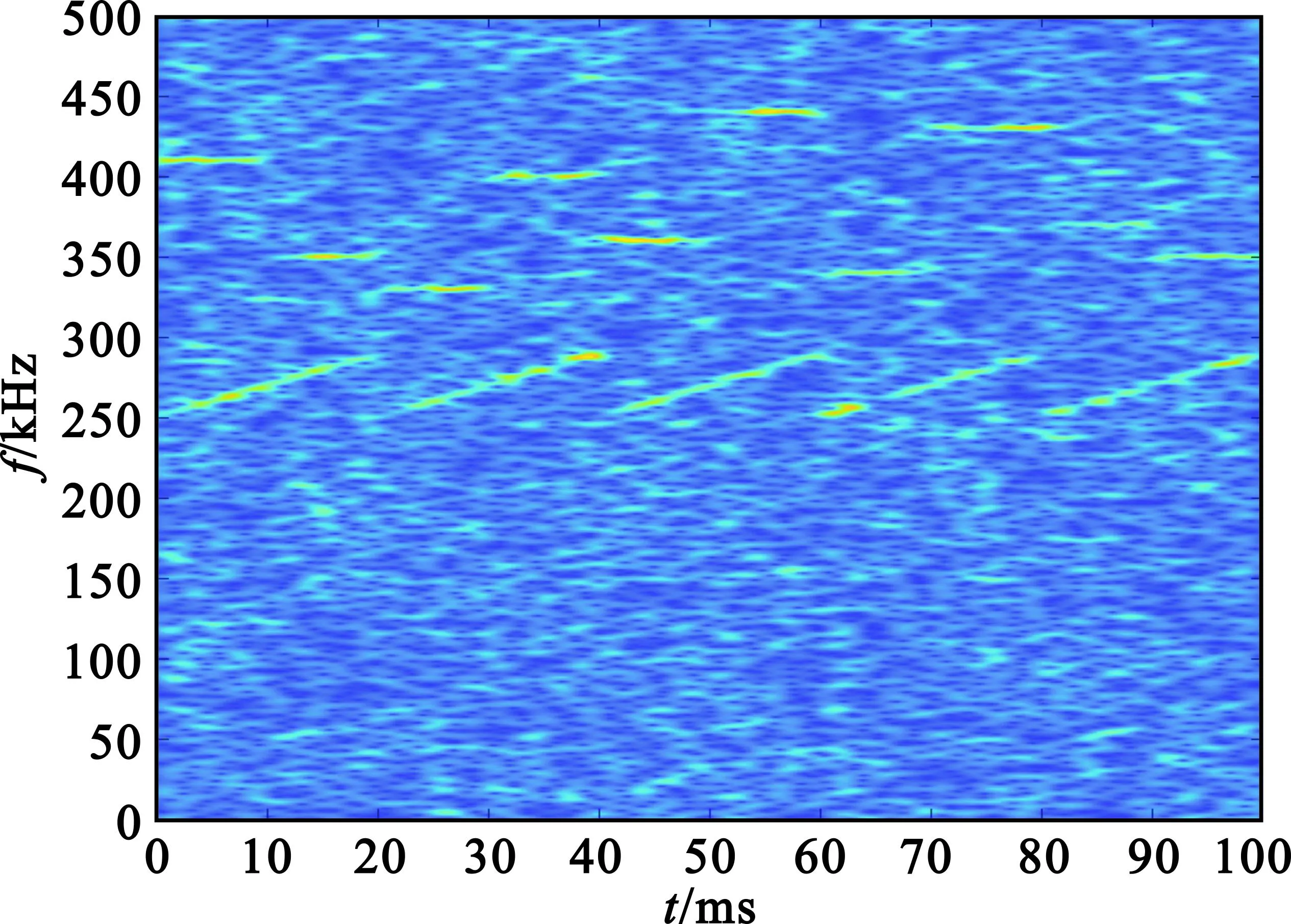
图3 接收端信号时频图像
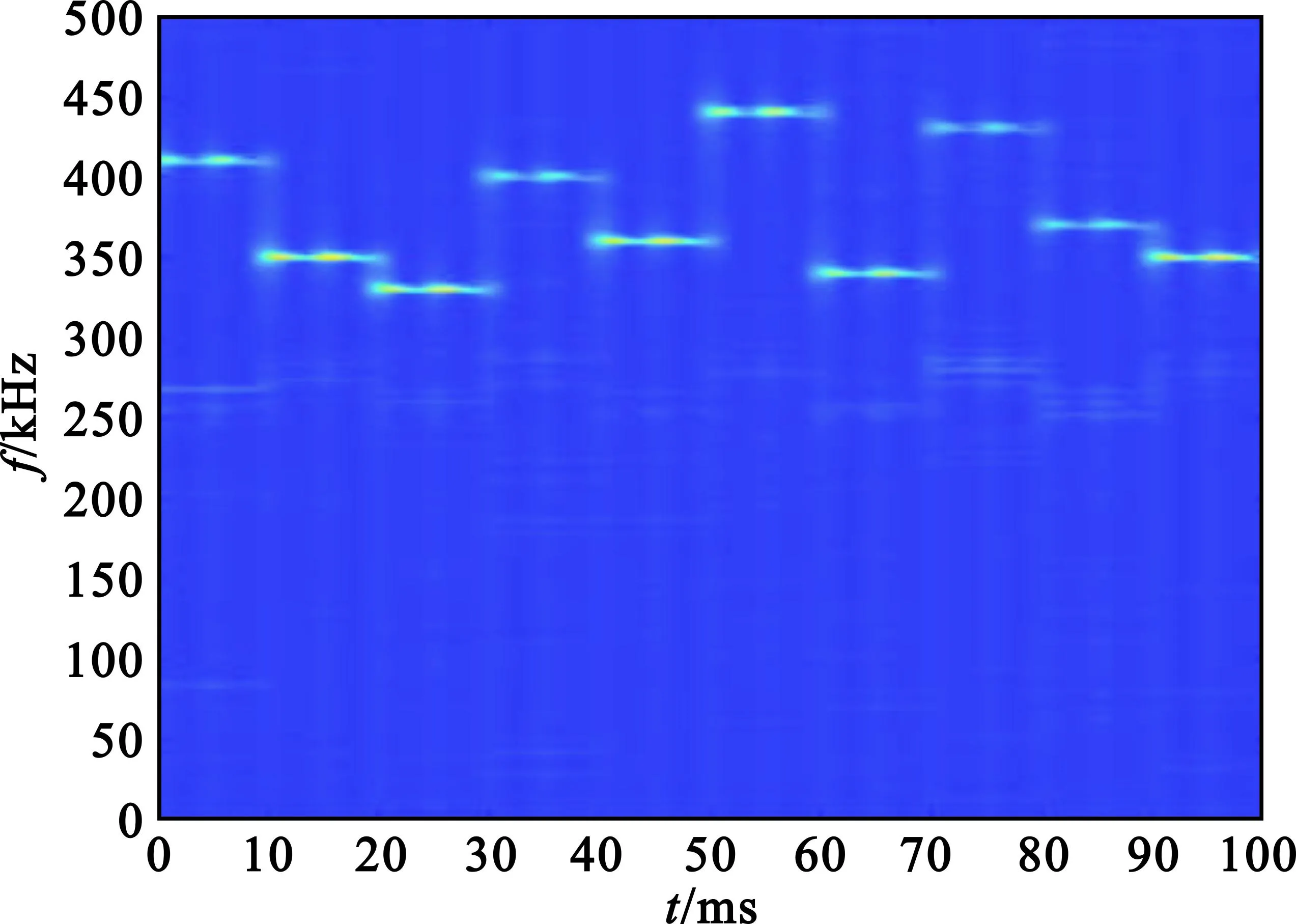
图4 预处理后信号时频图像
2.2 降噪提取
经过时频变换后,对时频图像进行降噪提取,主要有以下两个步骤:
1)二值化滤波
为获得更精确的参数估计值,需要获取清晰的时频图像,因此需要对时频图像作进一步降噪处理。通常采用阈值法对图像进行二值化,大于阈值μ的点赋值为1,小于等于阈值 的点赋值为0。计算过程定义如下:
(5)
阈值μ可采用迭代法[9]来计算。首先选取初始阈值μ1,由时频矩阵STFT的最大值STFTMax和最小值STFTMin决定:
μ1=STFTMax+STFTMin。
(6)
然后以μ1为阈值将时频矩阵分为STFT1和STFT2两个部分,其中,STFT1表示大于阈值μ1的部分,STFT2表示小于阈值μ1的部分,分别计算各部分的均值,表示为s1和s2:
(7)
式中:N1为STFT1中点的个数;N2为STFT2中点的个数。
根据下式计算得到新的阈值μ2:
μ2=(s1+s2)/2。
(8)
进行迭代运算不断获得新的阈值,直至μk+1=μk时,结束运算并获得最终阈值,并将阈值μk+1代入公式(5)进行降噪,得到二值化图像。图5为经过二值化处理后的时频图像。
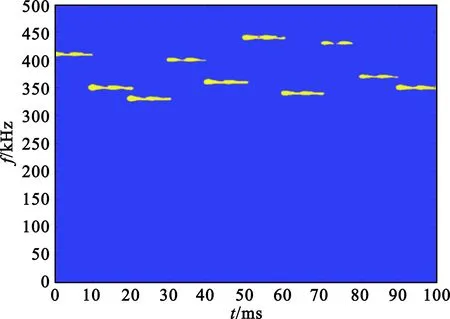
图5 二值化图像
2)形态学滤波
在干扰较强的情况下,二值化处理不能将所有干扰处理干净,同时也会有部分信号被当作干扰清除而导致跳频簇的时频图像不完整,形态学滤波可以较好地解决这个问题。形态学滤波是通过设定不同的结构元素对图像进行运算进而获取图像的局部特征[13]。膨胀运算、腐蚀运算、开运算和闭运算是形态学滤波的基本运算,其中,开运算可以消除干扰、平滑图像,闭运算可以填补空洞、弥补图像。开运算为先进行腐蚀运算再进行膨胀运算,可做如下定义:
Ft1(n,k)=Ft(n,k)∘b=(Ft(n,k)⊕SE)⊙SE)。
(9)
式中:Ft(n,k)表示待处理图像的时频矩阵;∘表示开运算;⊙表示膨胀运算;⊕表示腐蚀运算;SE表示结构元素。
闭运算为先进行膨胀运算,再进行腐蚀运算,定义为
Ft1(n,k)=Ft(n,k)·b=(Ft(n,k)⊙SE)⊕SE)。
(10)
式中:·表示闭运算。
构造结构元素是形态学滤波的关键环节,结构元素应大于需要消除的部分、小于需要保留的部分,这样才能获得较好地滤波效果。因此,本文中形态学滤波的处理流程和结构元素构造策略如下:
①对时频矩阵进行闭运算,用于弥合裂缝、填补空洞,因此构造小尺寸的矩形元素,本文中的矩形元素尺寸为3×100。
②对时频矩阵进行开运算,用于平滑图像,消除未处理干净的噪声点,完成形态学滤波处理。跳频簇在时频矩阵中表现为水平状态,因此需要构造水平线型元素,尺寸小于跳频簇的水平尺寸,大于噪声点的水平尺寸,本文中的线性元素尺寸为300。
图6为经过形态学滤波处理后的时频图像,可以看到基本完成跳频信号的提取,为接下来的参数估计做好了准备。

图6 形态学滤波后的时频图像
2.3 参数估计
采用聚类算法思想完成信号参数估计,重点在于对各个跳频簇聚类中心的计算。计算流程如下:
1)采用8连通标记算法完成对时频矩阵的区域划分,总计k簇跳频信号。图7为区域联通标记图像。
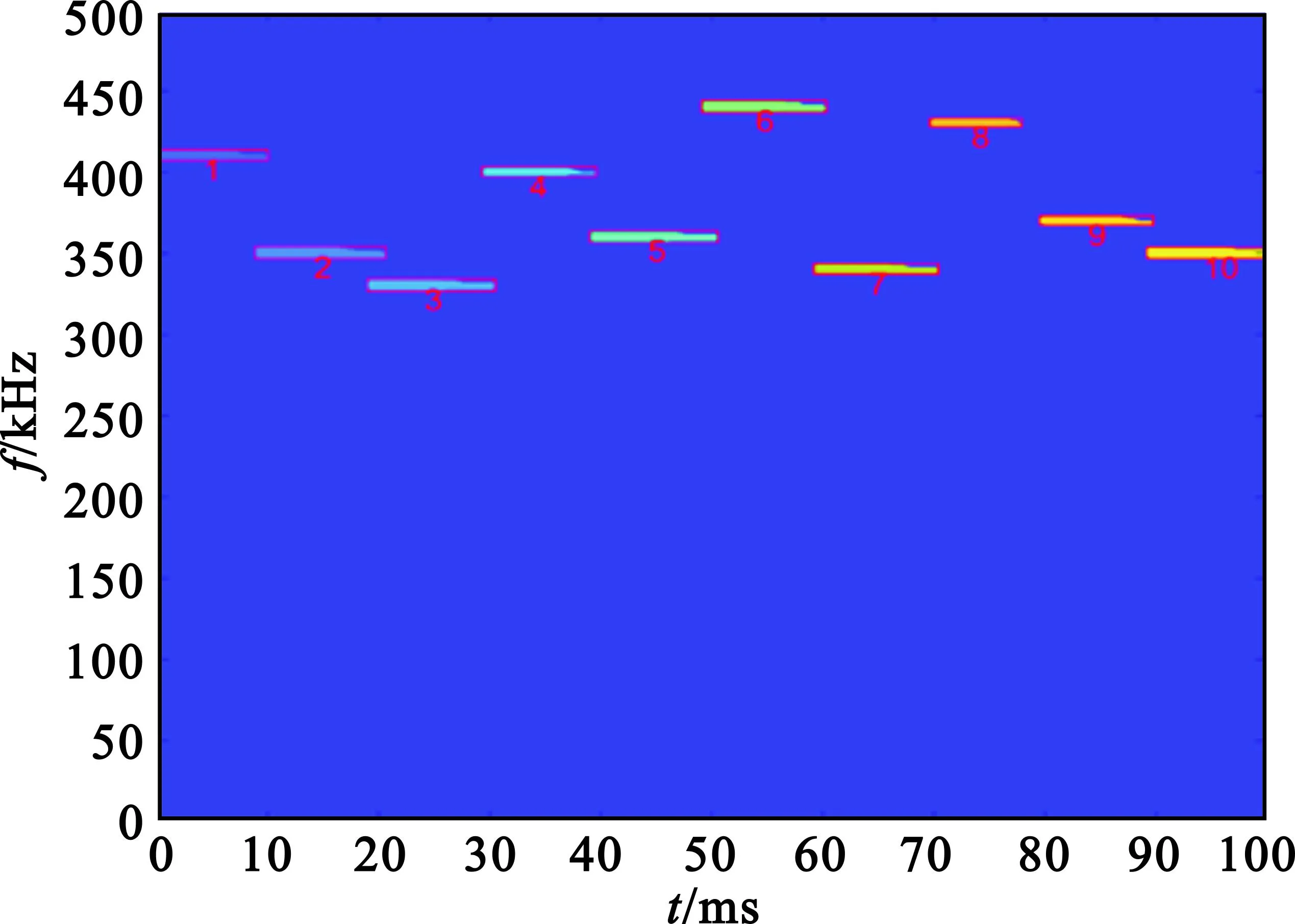
图7 区域联通标记时频图像
2)在跳频信号完成联通标记后,所有数据点被标记赋值,假设时频矩阵内数值为1的点的数量为N,提取时频矩阵内所有数值为1的点构成集合P={P1(t1,f1),P2(t2,f2),…,PN(tN,fN)},假设该跳频信号共计k个跳频簇,按照如下公式计算第i跳跳频簇聚类中心:
(11)
3)所有聚类中心构成集合C={C1(t1,f1),C2(t2,f2),…,Ck(tk,fk)},此时输出各聚类中心的频率坐标作为跳频频率参数估计值:
(12)
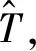
T(i)=(ti+1-ti)|i∈[1,k-1],
(13)
(14)
2.4 跳频参数估计算法模型
综上所述,本文算法具体步骤如下:
Step1 通过自相关算法对接收端信号进行降噪预处理,可去除白噪声和不含有周期特性的干扰信号。
Step2 采用STFT算法对信号进行时频变换,得到时频矩阵。
Step3 通过二值化和形态学滤波,完成对时频图像的降噪提取。
Step4 采用聚类算法的思想而完成跳频信号参数估计。
算法总体流程框图如图8所示。

图8 算法流程
3 仿真实验
为分析在不同信噪比条件下的算法性能,对测量误差做如下规定:
(15)
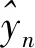
以下实验结果均是200次蒙特卡洛实验结果的平均值。
3.1 跳频频率和跳频周期的估计误差
设置采样率为1 000 kHz,频率集为[410,350,330,400,360,440,340,430,370,350]kHz,跳频周期为10 ms;设置扫频干扰,扫频范围250~300 kHz,扫频周期为20 ms;信号长度为100 000点,仿真时长100 ms,比较在不同强度高斯白噪声条件下本文算法与文献[6]和文献[9]算法的性能。
3种算法对跳频频率的估计误差如图9所示,对跳频周期的估计误差如图10所示。由图9和图10可见,本文算法在跳频频率估计和跳频周期估计方面都优于对比算法,而本文算法在信噪比低于-10 dB时性能大幅度下降,而文献[6]算法在低于-4 dB时性能开始衰减,文献[9]算法在低于-6 dB时性能开始衰减,因此本文算法在抗噪声性能方面更加稳定。
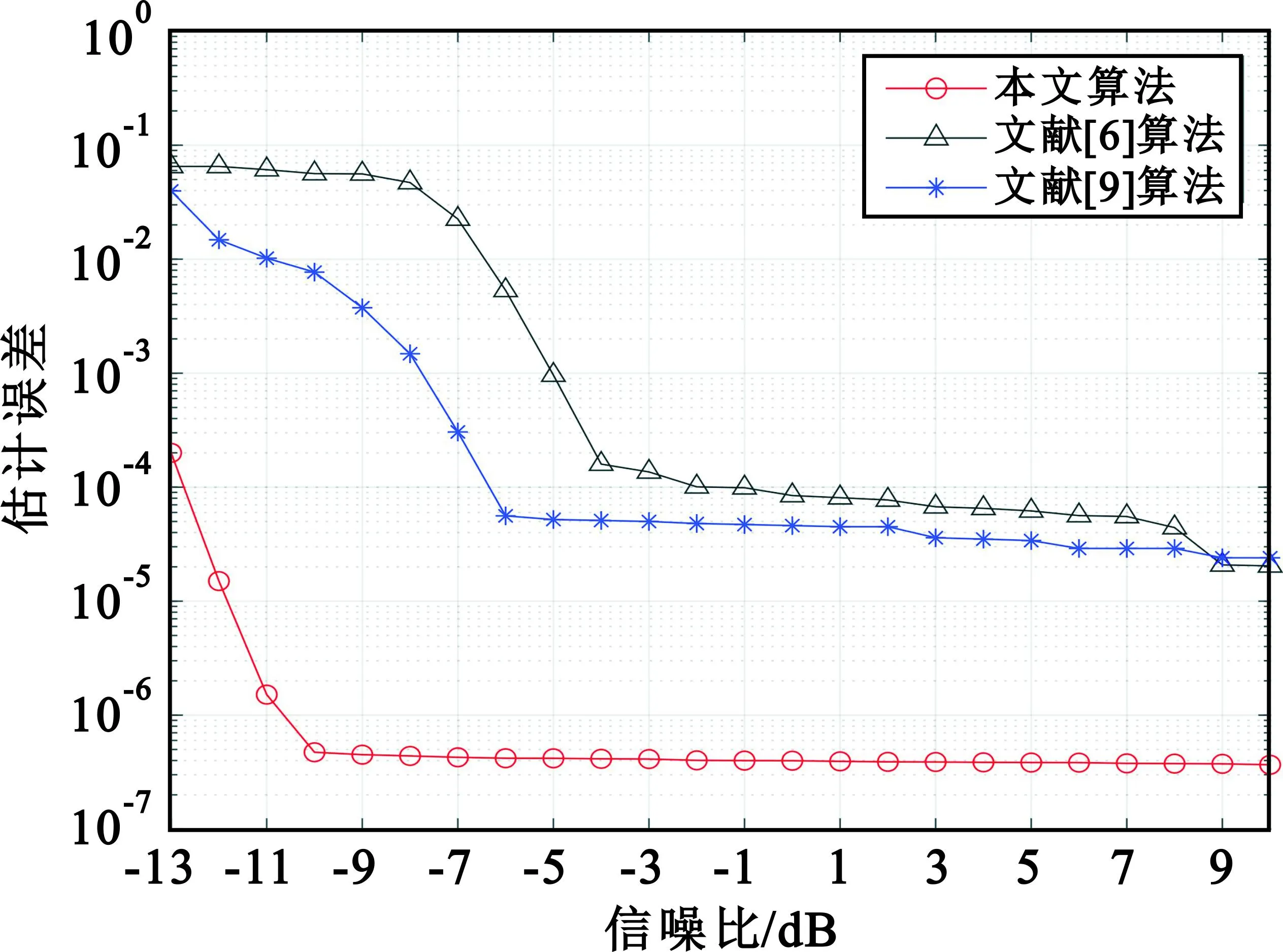
图9 跳频频率的估计误差
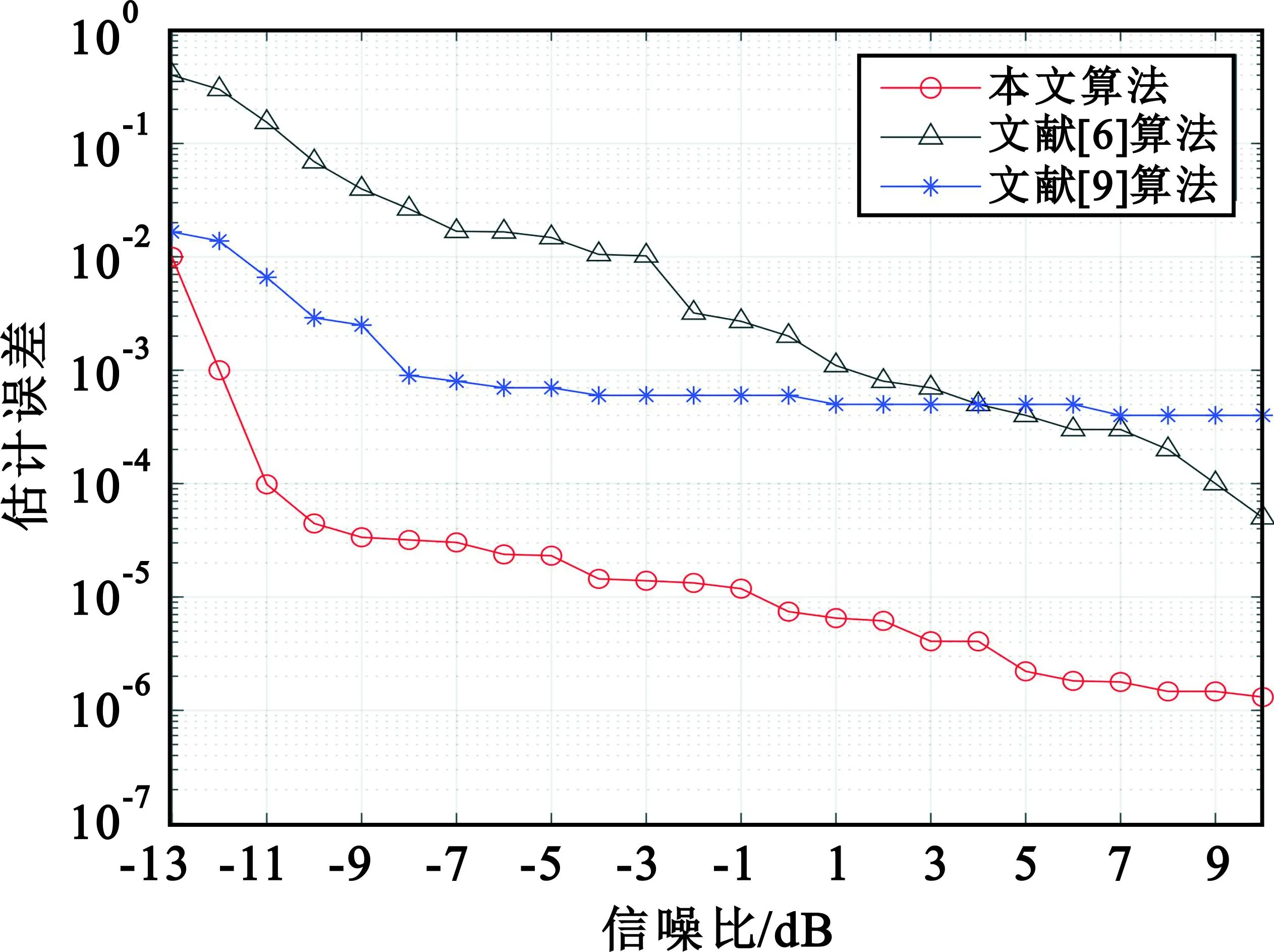
图10 跳频周期的估计误差
3.2 参数估计误差
由于查阅的资料中,很少有采用自相关运算对信号进行预处理,因此本实验将本算法有无自相关预处理作为变量之一,检验预处理过程对算法性能的影响。跳频信号的参数同3.1节,有无预处理的参数估计误差如图11所示。
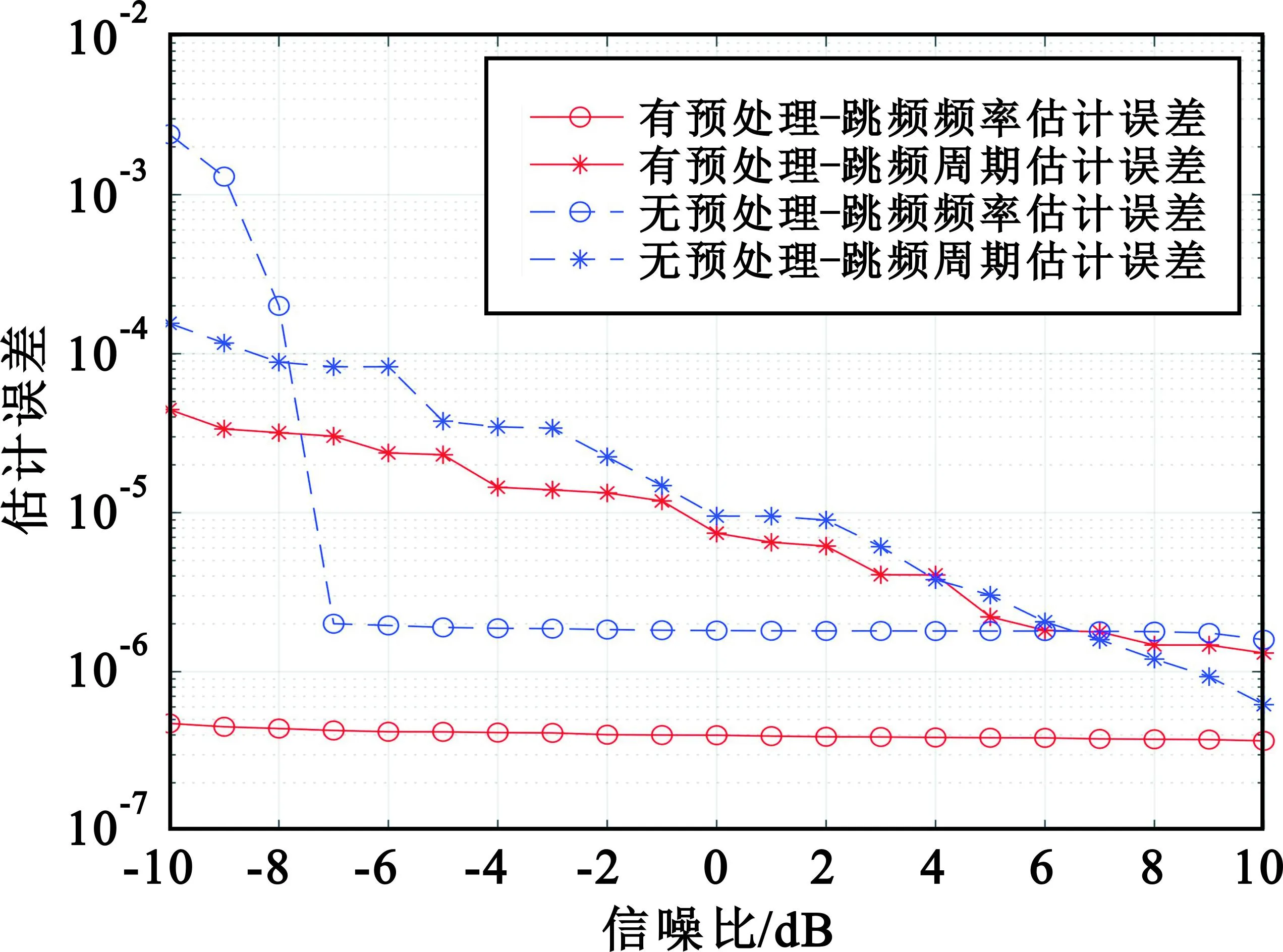
图11 有无预处理的参数估计误差
由图11可见,添加自相关预处理后,参数估计精度有不同程度提高;无预处理时,跳频频率估计性能在信噪比低于-7 dB后衰减较快,跳频周期估计无明显变化,由此可以判断自相关预处理可以使跳频参数估计在抗噪声性能方面有明显提升。
4 结 论
本文提出了一种基于自相关和时频分析的跳频参数估计算法,并通过仿真实验对算法性能进行了验证。本文算法通过对接收端信号进行自相关运算,有效消除高斯白噪声等无周期特性的噪声及干扰,通过STFT对信号进行时频变换,采用二值化和形态学滤波的方法完成降噪提取,最后通过聚类算法完成跳频参数估计。仿真实验表明,本文算法在低信噪比时具有较高的估计精度,同时验证了自相关运算可较大幅度提升算法性能。
