大型邮轮舷侧连续开口结构弯剪强度简化计算研究

2023-12-23胡鹏辉吴卫国

江苏科技大学学报(自然科学版) 2023年5期

敖雷,胡鹏辉,2,刘斌*,吴卫国

(1.武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心,武汉430063) (2.武汉理工大学船海与能源动力工程学院,武汉430063)

为满足大型邮轮复杂多样的功能布置需求,舷侧结构伴有大量的开口,其开口往往形式多样、位置各异、连续密集且开口率大,一些开口甚至横跨十余肋位.这些开口明显降低了舷侧外板的刚度,导致舷侧结构的抗弯剪性能显著下降[1].我国大型邮轮设计建造技术仍处于起步探索阶段,对邮轮舷侧连续开口结构的力学承载性能研究尚不深入,距完全掌握国产大型邮轮设计建造技术仍有一定的距离.分析大型邮轮舷侧结构在典型工况下的承载特性,研究舷侧结构的弯剪性能,可为大型邮轮舷侧结构设计及安全性评估提供参考依据.大型邮轮上层建筑舱室精细化程度高,如果通过全船有限元方法进行分析计算,有着建模工作量大、计算耗时长、网格模型不精确、计算资源要求高等缺点[2-3].舷侧外板的开口结构具有重复几何图形、阵列分布的特征,因此在对舷侧结构进行强度研究时,学术界普遍采用了简化分析方法,提取舷侧开口的主要结构特征进行简化建模[4].文献[5]提出了一种以正交异性平面单元和杆单元组合表示大型客船舷侧开口加筋板的方式,提出了3种局部等效简化模型,通过比较多甲板多开口的简化船体梁的二维和三维有限元模型理论计算结果,详细研究了该方法的精度.文献[6]提出了多甲板船舷侧开口简化建模方法,并通过大型邮轮的有限元仿真分析,验证了所提出的简化建模方法.文献[7]提出一种船体梁模型简化方法,比较了完整模型与简化模型的极限弯矩,验证了该简化方法对于分析船体梁极限弯矩的可行性.文献[8]提出了一种评估上层建筑有效性的简化模型,将船体的三维结构简化为二维模型,较好地模拟了上层建筑和主甲板结构间的相互作用,从而简化上层建筑参加船体总纵弯曲程度的计算.文献[9]提出了一种简化的建模方法来模拟整个邮轮的复杂结构,采用非线性有限元分析方法分析了船体梁的极限强度和失效模式,总结了上层建筑结构有效性从弹性状态到极限状态的变化特性.文献[10-12]针对大型客船的各种开口加筋板结构开展了极限强度试验研究.文献[13]研究了邮轮在总纵弯曲作用下的崩溃特性和极限强度,并开展了大型邮轮结构崩溃试验.目前,舷侧开口简化模型的研究主要以舷侧局部开口结构为研究对象,且研究舷侧开口结构抗剪强度居多,针对大型邮轮含开口舷侧结构弯剪强度的研究较少.本文以某大型邮轮含开口舷侧结构为研究对象,基于劳氏船级社规范中的多甲板大型客船上层建筑舷侧开口结构强度校核评估计算方法[14],提出了一种舷侧结构简化模型,采用ABAQUS有限元软件分析含开口舷侧结构在波浪载荷作用下的弯剪强度,验证了简化计算模型的有效性,为舷侧结构设计提供了一种快速建模及分析方法.

1 舷侧结构简化模型

以某大型邮轮为研究对象,建立了全船半宽模型,其中横剖面如图1.模型长313.2 m,宽18 m,高41.1 m,甲板、舷侧外板、舱壁的板厚以及各种加筋和扶强材的尺寸均在图1中有所表示.根据劳氏船级社提出的客船舷侧结构强度校核评估计算方法,将甲板2以下主船体结构简化为箱型梁,甲板2以上的每层甲板简化为附着在舷侧外板上的梁单元,建立以舷侧连续开口结构为主体的简化计算模型(图2),用于分析船体梁受总纵弯曲作用下舷侧结构抗弯剪载荷的承载特性.其中,第2～4甲板间的开口为观景窗开口,第4～6甲板间的开口为落地窗开口,第6甲板以上的连续开口是为了模拟分布在邮轮左右两舷海景房的门窗开口结构.

图1 全船半宽模型中横剖面

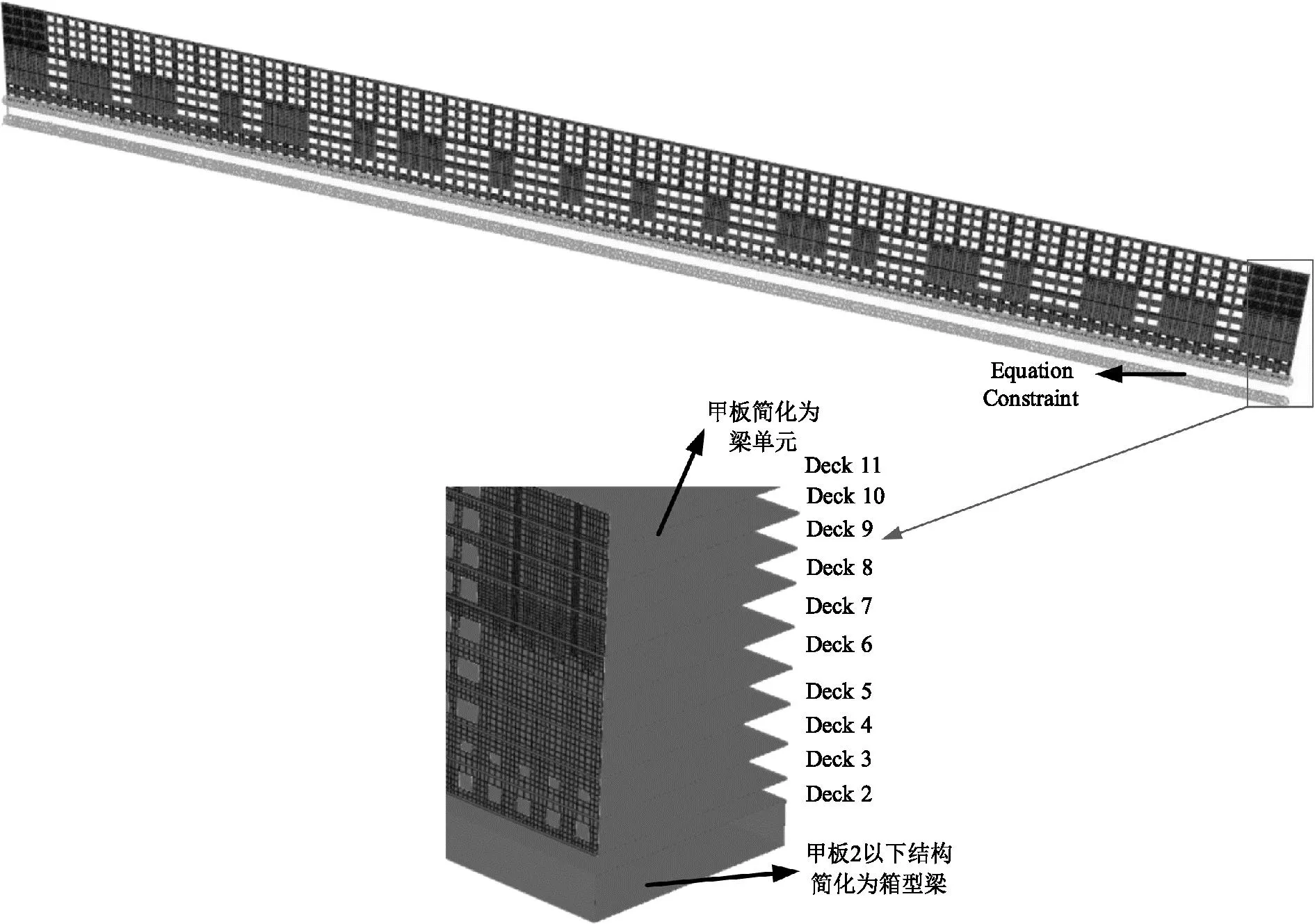
图2 舷侧简化模型

为保证主船体结构和甲板2以上的每层甲板简化为梁单元后总体刚度和承载性能的一致性,首先计算出主船体结构和甲板2以上的每层甲板的剖面惯性矩以及横截面积(表1),使简化的各梁单元的惯性矩及横截面积与对应的结构相等.其中,由主船体结构简化而成的箱型梁单元处于整个甲板2以下结构的中和轴上.箱型梁单元节点与甲板2梁单元相应节点采用Equation Constraint建立位移约束关系,使箱型梁与甲板2在垂直方向上的位移相同.模型简化计算流程如图3.甲板2以上结构材料采用AH36高强度钢,主船体结构采用A级钢,材料参数如表2.

表1 结构剖面惯性矩及横截面积

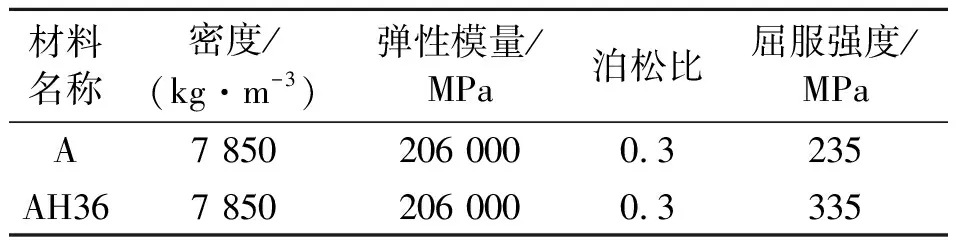
表2 材料参数

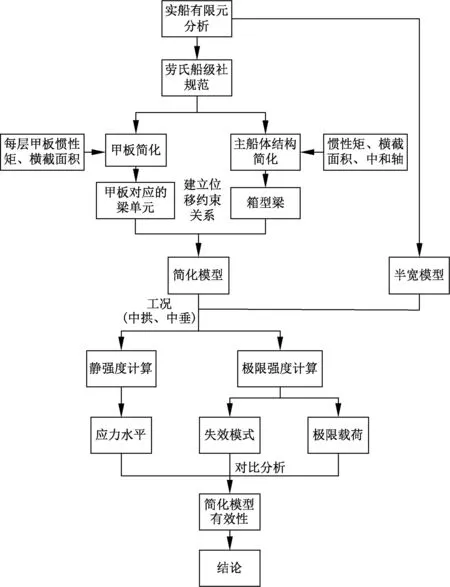
图3 模型简化计算流程

2 舷侧简化模型验证

2.1 舷侧简化有限元模型

选用ABAQUS软件对舷侧结构进行有限元分析,舷侧简化有限元模型网格大小选取为500 mm,包含36 992个壳单元,43 159个梁单元,44 464个节点.模型的边界条件定义及载荷施加如图4,模型左侧底部端点处约束Y、Z方向的位移,模型右侧底部端点约束X、Y、Z方向的位移.参照中国船级社《邮轮整船直接计算指南》[15],沿船长施加分布力进行加载,分布力为:

图4 舷侧简化模型边界条件

(1)

式中:MW为船中波浪弯矩,kN·m;LO为船长,m;x为计算点在整船模型中的相对坐标,模型尾端为0,模型首端为1;系数a1、a2、a3、a4为船长尾端之后与船长前端之前的模型长度相对于船长的比例系数,文中取a1=7.841,a2=-1.457,a3=-20.609,a4=14.225.

2.2 全船半宽有限元模型

全船半宽有限元模型网格大小选取为500 mm,包含616 076个壳单元,311 722个梁单元,596 268个节点.模型的边界条件定义及载荷施加如图5,Ux、Uy、Uz分别为沿X、Y、Z方向的位移,Rx、Ry、Rz分别为沿X、Y、Z方向的转角.模型两端底部所有节点约束Y方向的位移,模型中纵剖面所有节点使用对称约束Uz=Rx=Rz=0,在右端底板与中心纵截面相交处的节点施加约束Ux=Uz=Rx=Rz=0,左端底板与中心纵截面相交处的节点施加约束Uz=Rx=Rz=0.半宽模型的加载方式与舷侧简化模型相同.

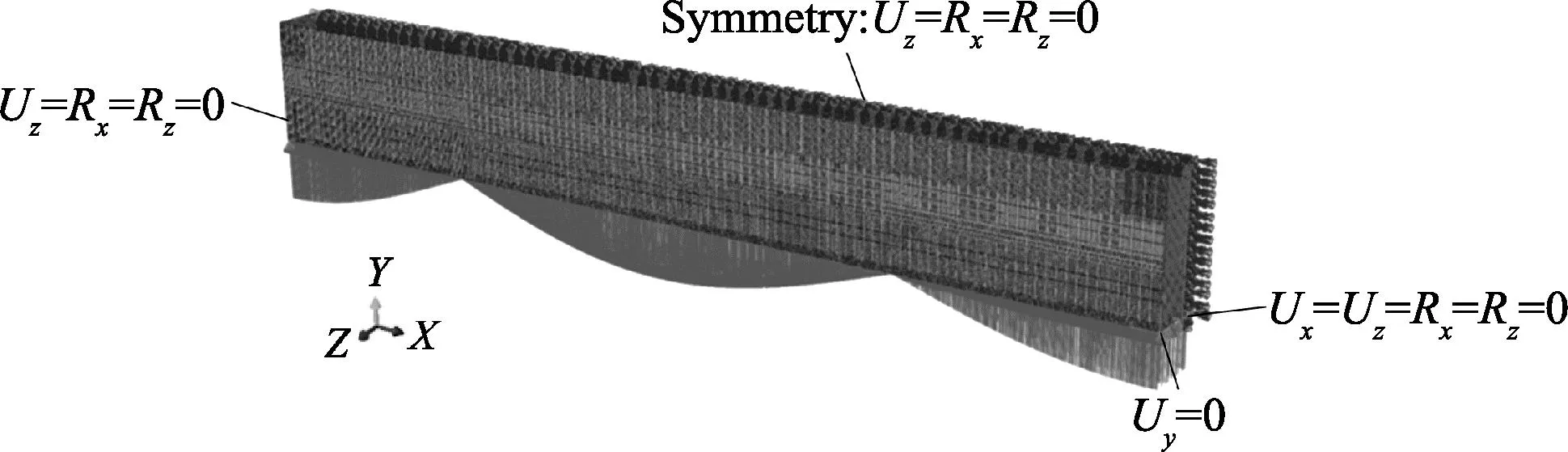
图5 全船半宽有限元模型

2.3 静强度分析

静强度分析计算工况采用中垂和中拱工况,加载方式由式(1)给出,MW取值为中垂MW(-)和中拱MW(+)波浪弯矩,其值由式(2)、(3)给出:

MW(-)=-0.11MCL2B(Cb+0.7)

(2)

MW(+)=0.19MCL2BCb

(3)

式中:M为弯矩分布系数;L为模型总长;B为模型宽度;Cb为方形系数;C为波浪系数.

对舷侧简化模型和全船半宽模型开展结构静强度计算,Von-Mises应力对比如图6～7.对于舷侧简化模型,从图6中可以看出中垂工况下,应力较大的区域主要集中在第6甲板至第10甲板间的连续开口处以及舷侧外板的顶部,此外舷侧外板开口角隅处出现了应力集中现象,最大应力为222.6 MPa.全船半宽模型的舷侧外板应力分布水平与舷侧简化模型大致相同,模型的连续开口处的应力水平较高,模型的顶部应力较大,舷侧外板开口处也存在应力集中现象,最大应力为231.0 MPa,误差为3.6%.在中拱工况下,舷侧简化模型与全船半宽模型的应力分布基本一致,应力最大的地方同样是在6甲板至第10甲板间的连续开口处,最大应力值分别为200.2、214.7 MPa,误差为6.7%.

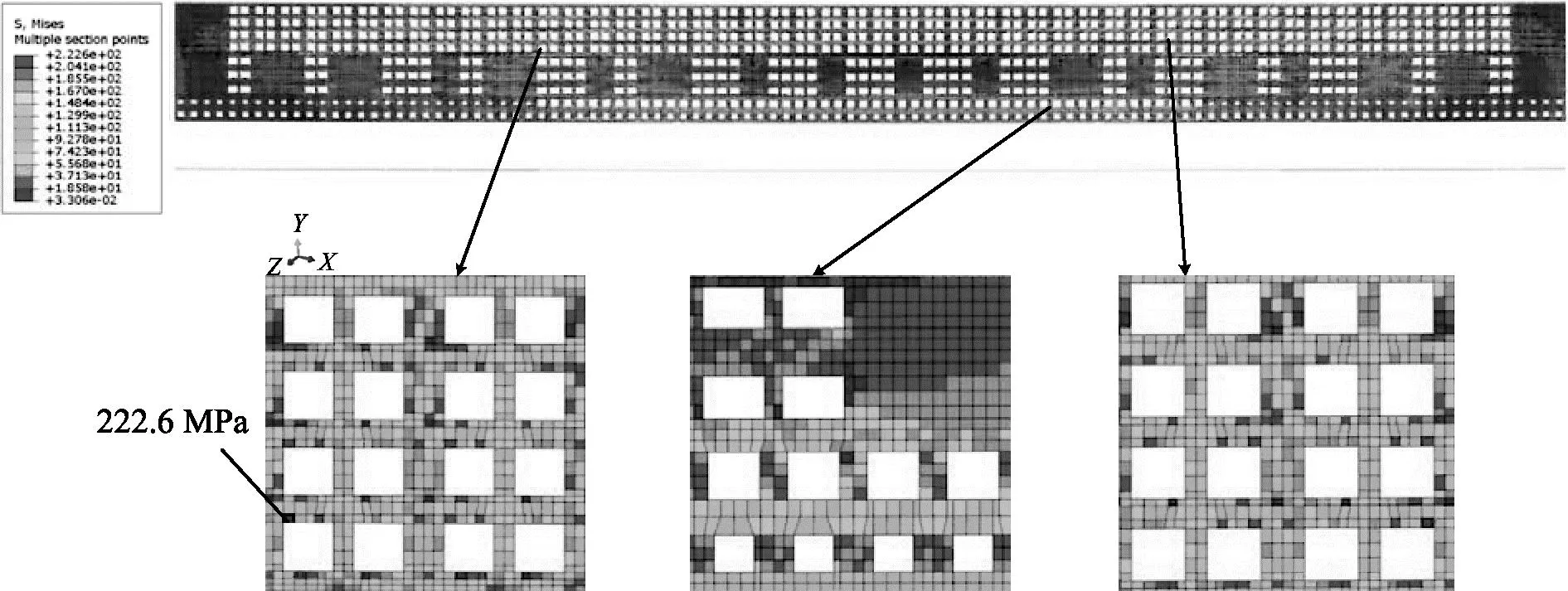
图6 舷侧简化模型应力分布(中垂工况)

图7 全船半宽简化模型应力分布(中垂工况)

3 极限强度分析

3.1 弯矩—位移曲线

对舷侧简化模型和全船半宽模型开展结构极限强度计算,图8为舷侧简化模型和全船半宽模型在中垂工况下弯矩—位移关系.在非线性计算过程中,底部分布荷载逐渐增加,直到结构失效.舷侧简化模型在中点的极限弯矩值为8.59×1012N·mm,全船半宽模型中部极限弯矩值为8.87×1012N·mm,误差为3.1%.图9为舷侧简化模型和全船半宽模型在中拱工况下弯矩—位移关系.舷侧简化模型在中点的极限弯矩值为9.69×1012N·mm,全船半宽模型中部极限弯矩值为1.05×1013N·mm,误差为7.7%.

图8 弯矩—位移曲线(中垂工况)

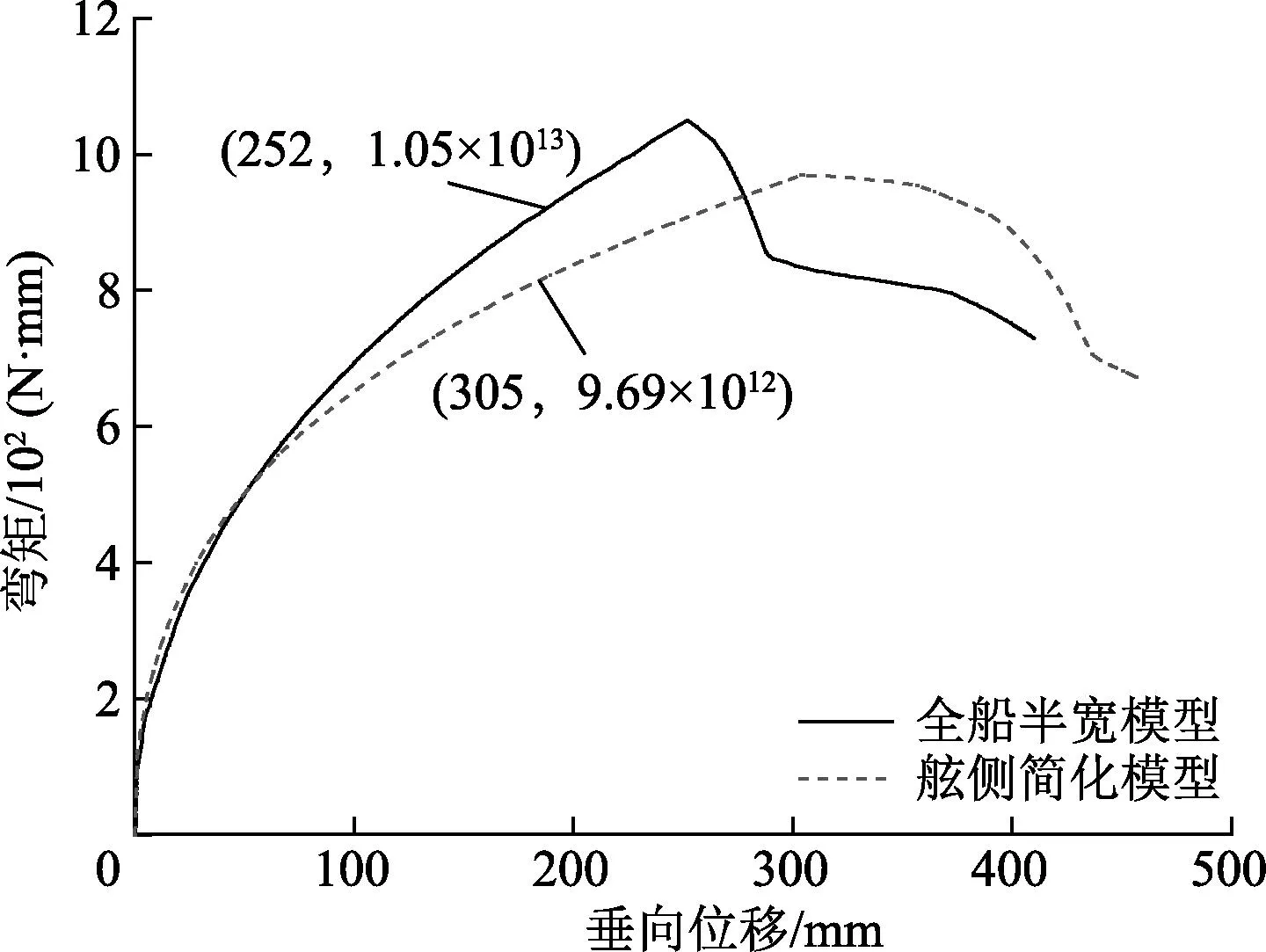
图9 弯矩—位移曲线(中拱工况)

3.2 失效模式

舷侧简化模型在中垂工况下的破坏模式如图10,从图中可以看出,舷侧简化模型底部结构受到张力作用开口外侧发生了屈曲破坏,模型中部两侧的连续开口结构在剪力的作用下出现了屈曲失效,随着分布载荷的增加,失效范围逐步向两侧增加.

图11为全船半宽模型在中垂工况下的破坏模式,可以看出模型的连续开口结构同舷侧简化模型一样发生了明显的屈曲破坏,并逐渐向两侧扩散,上层建筑顶层甲板发生了严重的屈曲变形,侧外板底部开口也出现了屈曲失效.在中拱工况下,舷侧简化模型与全船半宽模型甲板2～4间的开口首先发生屈曲破坏,引起局部结构失效,随着载荷继续增加,甲板6～10间的连续开口结构也发生了屈曲破坏,最终导致整个舷侧结构失效.

图11 全船半宽模型失效模式(中垂工况)

3.3 模型简化前后对比

模型简化前后的单元数量、计算时间、应力大小、极限强度对比如表3.文中提出的舷侧简化模型与全船半宽模型相比,极大地减少了建模工作量,节约了计算资源,短时间就可完成对舷侧开口结构的建模及强度分析.

表3 模型简化前后对比

对比模型的静强度和极限强度计算结果,可以发现静强度相较于极限强度的计算结果精准性高.由于极限强度分析涉及材料、几何非线性,简化方法无法精准模拟简化区域结构的几何大变形和塑性失效,因此通过简化方法分析目标船体梁的总纵极限弯矩误差更大.然而所提出的简化模型可快速评估含开口舷侧结构的极限载荷及失效模式,为含开口舷侧结构的初始设计提供了简便的分析方法.