基于双层随机优化的农村能源系统规划设计方法

2023-12-22刘明浩霍红阳韩中合吴智泉

可再生能源 2023年12期

刘明浩，霍红阳，韩中合，吴智泉

(1.华北电力大学，河北保定 071000；2.国家电投云南国际电力投资有限公司，云南昆明 650100）

0 引言

随着“双碳”战略的逐步实施，农村能源开发利用面临着众多挑战。首先，能源设备建设容量的选取是能源低碳利用面临的首要问题。一方面，农村地区的能源设备须要有足够的建设容量以满足能源需求的增长；另一方面，为确保设备运行的可靠性和经济性，需要对能源设备的建设容量进行科学合理的规划和配置。其次，新能源出力随机性会影响能源系统的设备容量和运行策略，如何在随机性条件下确保能源供应的稳定性也是须要考虑的问题之一。总之，农村能源系统合理的容量配置与运行调度，对农村能源开发利用具有重要意义。

以往的研究已在农村能源体系优化方面取得进展，包括推广生物质清洁供暖[1]、创建集成多种设备的虚拟电厂模型[2]，以及多目标的优化等[3]。此外，还有研究提出了三方博弈模型，分析政府、新能源企业和农民在能源产业转型中的演化路径和稳定策略[4]。然而，已有的研究大多关注于设备容量规划或者运行阶段的能源系统优化，而未深度耦合设备容量规划和后续系统综合运行优化之间的关系。能源设备的容量规划会影响后续的运行优化，而能源设备的运行决策是容量规划的重要参考依据。为达到前期建设和后期运行之间的平衡，须要将设备容量规划和系统运行优化紧密结合起来。

农村地区的数据收集困难，导致风、光出力预测困难，其随机性对系统稳定供能和用户用能安全性产生重要影响。已有研究在处理风、光出力随机性[5]，[6]，降低最优储能容量运行成本[7]以及考虑预测误差的影响[8]方面做了详尽的研究，但鲜有研究考虑随机参数对容量配置与能量调度之间耦合关系的影响。实际上，新能源的随机性可能会破坏能源系统的供需平衡，在优化过程中，须要考虑随机参数对容量配置与能量调度之间的相互作用，以实现最优的能量供应和调度策略。

综上所述，亟待开展考虑新能源出力随机性的农村能源系统容量配置和运行优化研究。本研究设计一种多目标双层优化模型，在满足农户冷、热、电负荷需求的同时，深入挖掘系统在经济成本、碳排放效益以及新能源消纳方面的潜力。上层模型基于多目标粒子群算法(Multi-Objective Particle Swarm Optimization，MOPSO）寻找系统最优容量配置，考虑了设备的投资成本和设备全寿命周期碳排放，下层模型采用混合整数线性规划程序(Mixed Integer Linear Programming，MILP）计算系统最优运行成本。综合考虑不同季节下的风、光随机出力场景，使计算结果更加符合农村地区实际需求。通过不断耦合、调整、迭代上下层模型参数，得到多目标pareto最优解集。运用本文提出的模型，对北方某农村地区的能源配置和运行情况进行了案例分析，为促进农村地区综合能源系统的建设和运行提供理论支持。

1 农村能源系统的结构与主要设备

本文所构建的农村能源系统主要由燃煤采暖炉设备(Coal-fired Furnace，CF）、生物质热能锅炉(Biomass Boiler，BB）、风力发电设备(Wind Turbine，WT）、光伏发电设备(Photovoltaic，PV）、电储能(Electric Energy Storage，EES）、热泵(Heat Pump，HP）、电制冷(Electric Chiller，EC）设备等组成，其结构如图1所示。能源供给侧依靠农村电网、风、光、生物质、煤炭联合实现电力及热力供应，储能设备用于消纳新能源电力；能源需求侧主要包括电、热、冷3种负荷，居民生活电负荷由PV，WT，EES、电网直供共同承担，冷负荷由EC提供，热负荷则由HP，CF以及BB共同承担。

图1 农村多能源系统结构Fig.1Structure of rural multi-energy system

1.1 燃煤采暖炉运行特性

CF通过燃烧煤炭产生热能，其运行特性可由下式描述：

式中：Pcf为CF的制热功率；Fcf为CF消耗的煤炭质量；ηcf为CF的热转换效率；Hcf为煤炭的热值。

1.2 生物质热能锅炉运行特性

BB以生物质能源为燃料，提供热水形式的热能，其运行特性可由下式描述：

式中：Pbb为BB的制热功率；Fbb为BB消耗的生物质燃料质量；ηbb为生物质热转换效率；Hbb为生物质的热值。

1.3 热泵设备运行特性

HP设备输入为电能，输出为热能，其运行特性可由下式描述：

式中：ηhp为HP的电热转换效率；Php,in为HP输入的电能；Php,out为HP输出的热能。

1.4 电制冷设备运行特性

EC设备输入为电能，输出为冷能，由于农村地区人员分散，EC设备采用分布式布置的方式，通过村级电网传输EC所需的电力，从而满足农村居民冷负荷需求。其运行特性可由下式描述：

式中：ηec为EC的能量转换效率；Pec,in为EC的输入功率。

1.5 储能运行特性

EES是多时段设备，其运行状态受到以往时刻运行状态的影响，其运行特性可由下式描述：

1.6 风电设备运行特性

WT的发电功率取决于风速和装机容量，其出力情况可表示为

式中：Pwt，ava为WT的可用功率；为WT的额定功率；v为实时风速，vin，vout，vr分别为切入、切出和额定风速。

1.7 光伏设备运行特性

PV的发电功率取决于太阳辐射度以及装机容量，其实时输出功率为

式中：Ppv，ava为PV的可用功率；Spv为光伏阵列占地面积；ηpv为光-电能量转换率；r为t时刻太阳光直射辐射度。

1.8 能源系统耦合运行特性

前述建立了能源系统各设备的运行特性，为实现能源系统协调运行，需对各设备出力情况进行耦合，从而将各设备组合成为一套能源系统。该能源系统输出功率矩阵可描述为

式中：Pe,out，Ph,out，Pc,out分别为能源系统输出的电、热、冷功率；ηgrid，ηeline，ηrline分别为电网电力传输效率、能源系统内部电力传输效率、热网传输效率。

2 基于双层随机优化的农村能源系统设备容量规划和运行优化模型

2.1 目标函数

为确保农村能源系统的高效运行，须确定各个设备的最大建设规模，在此基础上，进行设备的运行优化。为此，建立容量-运行双层优化模型，其中上层模型用于各能源设备容量规划，下层模型用于优化能源系统运行，从而实现总成本、总碳排放以及新能源消纳率最优的目标。模型的总体目标函数如下：

式中：TI，TC分别为系统总经济成本、总碳排放量；TI1，TC1为上层模型目标函数，表示系统设备的投资成本以及设备的全生命周期碳排放量；TI2，TC2，γ分别为下层模型目标函数，表示系统运行成本、运行过程中的碳排放量以及新能源(光伏、风电）消纳率。

上层模型选取农村能源系统项目周期内的经济性能和环保性能作为评估指标，经济性能为各能源设备的建设投资成本，环保性能为各能源设备全寿命周期的碳排放量。能源设备包含CF，PV，WT，EES，BB，HP以及EC。为简化计算，设定计算周期为1 a，在该计算尺度内，建设投资成本可用等年值投资成本代替：

式中：CRFi为设备i的资本回收系数；Fi为设备i的单位投资成本；Ci为设备i的新增容量；r为资本年利率；li为设备i的可用年数。

能源设备在生产、运输和销毁过程产生的碳排放称为设备全寿命周期碳排放。由于规划周期为1 a，因此采用等年值全寿命周期碳排放表示全寿命周期碳排放：

式中：Ri为设备i的全寿命周期碳排放量。

下层调度优化模型以1 d作为调度尺度，旨在确定能源设备安装容量后，对能源系统内部各设备运行出力进行优化。其中，经济目标如式(15）所示，碳排放目标由式(16）表示，新能源消纳目标由式(17）表示。

2.2 能源设备容量配置模型

2.2.1目标函数

上层的能源设备容量配置模型的目标函数如式(12）～(14）所示。

2.2.2约束条件

农村自然资源、场地、改造资金等因素对能源设备的布置容量有一定影响。为保证系统能够正常运行，限制系统设备容量在一定区间内，即：

2.2.3优化变量

上层模型为规划模型，定义变量为每种能源设备新增的容量配置。

2.3 农村能源系统调度运行模型

2.3.1目标函数

下层的能源系统调度优化模型的目标函数如式(15）～(17）所示。

2.3.2约束条件

农村综合能源系统内部存在多种能源之间的耦合及平衡，包括冷、热、电、气等能源的节点能量平衡和负荷供需平衡，与此同时还须要考虑各种能源设备的运行出力情况。因此，须要根据现实条件对各类能源和能源设备施加约束。

①负荷供需平衡约束

能源系统输出能量须满足负荷需求，能源系统的负荷平衡约束可由式(20）～(22）描述。在平衡方程中，电负荷节点须要满足等式约束，热负荷节点和冷负荷节点由于具有一定的运行特性，仅须满足不等式约束即可。

②设备出力约束

各设备出力受制于上层模型规划情况，可用式(23）描述。

WT，PV发电功率取决于当前时刻的风力和光照情况，如式(24）～(27）所示。

③EES约束

EES的电量过高或过低会降低设备寿命，须为EES电量设置上、下限，同时设置EES的充/放电功率不超过最大充/放电功率，具体可描述为

④电网出力限制

2.3.3优化变量

结合农村能源供应现状，设置能源系统运行可调节参数为各个能源设备的出力情况，其中具有碳排放属性或价格属性的参数是影响模型目标函数的关键。为达到优化目的，设置的调整变量包括能源系统各设备的出力、EES充放能以及能源系统与电网之间的交互功率，可概括为

2.4 新能源出力随机性分析

农村地区WT的输出功率与风速大小直接相关，采用文献[9]中的Weibull函数描述风速分布：

式中：v为实时风速；α和 β分别为形状参数和尺度参数。

PV出力由辐射度决定，采用文献[10]中的Beta函数描述太阳能辐射分布情况：

式中：r为太阳直射辐射度；αp，βp分别为Beta函数中描述形状分布的变量。

得到风、光概率分布模型和出力计算式后，利用蒙特卡洛抽样法从概率分布函数中采样，生成风、光出力场景，并采用向后缩减法[11]将风、光场景缩减至5个。

2.5 基于粒子群和混合整数线性规划求解多目标优化问题

上、下层模型均为多目标优化问题，上层模型可通过MOPSO算法部署多个目标函数，下层模型是混合整数线性规划问题，仅支持单目标函数的计算。为实现上、下层模型之间的迭代，基于ε-约束法分析解决下层混合整数线性规划问题[12]，将下层模型的运行成本作为目标，将运行碳排放量和新能源消纳率设置为约束条件进行求解，优化模型见式(36）。

式中：ε1和 ε2分别为下层运行优化问题的碳排放量限制和新能源消纳量限制，由上层模型生成。

由于所采用的 ε-约束法为上层模型增加了自变量个数，因此，须为上层模型创建 ε1和 ε2的约束条件：

ε1和 ε2与式(19）中的X1一同作为MOPSO的自变量，根据MOPSO的不断迭代而变化。

在能源设备容量与运行优化模型中，上层模型采用MOPSO算法进行迭代，下层模型使用cplex求解器求解。由各设备装机容量以及碳排放量和新能源消纳量组成的上层模型的输出参数作为下层模型的输入参数，下层模型的目标函数值返回上层模型进行迭代。图2为双层模型求解的算法流程。

图2 综合能源系统双层优化模型求解流程Fig.2 Solution flow of two-layer optimization model for integrated energy system

图2中的双层模型求解优化问题的流程可描述如下。

①首先生成风、光出力场景，将风、光出力场景各缩减至5个。

②初始化种群和全局最优粒子，根据上层模型约束条件随机生成N个粒子，迭代次数i=1。

③将每个粒子所携带的参数输入下层模型进行求解，若优化可行，则返回目标函数值TI2以及约束条件TC2和 γ，结合该粒子上下层模型的目标函数值计算粒子适应度函数值；若不可行，则返回不可行标识，对于不可行粒子，不进行计算，该粒子将直接进入下一循环阶段。

④将全局最优粒子和当前种群放在一起进行pareto排序，更新全局最优粒子，更新当前每个粒子的最优位置。

⑤更新粒子的速度和位置，为避免算法陷入局部最优，对部分粒子的速度和位置进行扰乱。

⑥若迭代次数达到max_i，则终止迭代。否则，重复步骤③～⑤。

3 北方某典型村能源系统容量配置与运行优化分析

为验证能源系统设备容量与运行优化模型的有效性和适用性，选择北方某典型村作为算例。选择该村有两个主要原因：第一，该村拥有丰富的风、光资源，具有较好的新能源开发潜力；第二，该村已经完成农村电网的改造建设，大部分住户已经接入了农村电网，为实现能源系统改造优化提供了基础。

3.1 典型村负荷基本数据

典型村位于黑龙江省中南部，松花江中游北岸，年平均日照时数为2 542 h，有相对丰富的太阳能资源；一年四季风速较高，年平均风速为7.62 m/s，风力资源充沛。选取4个季节的典型日进行分析，在典型日内电、热、冷负荷如图3(a）所示，风、光随机性出力的场景缩减结果如图3(b）所示。其中，0～24 h为春季数据，24～48 h为夏季数据，48～72 h为秋季数据，72～96 h为冬季数据。

图3 典型村基础数据Fig.3 Basic data of typical village

优化模型的计算还需要一些基础数据，如能源设备价格、全生命周期碳排放量、使用寿命，以及各类能源的价格与碳排放强度。将模型的基础数据列于表1～3。其中，设备的基础数据如表1所示，各类能源的基础数据如表2所示，电网电力价格如表3所示。此外，将电网电力的碳排放强度设定为0.65 kg/(kW•h）[1]。

表1 设备基础数据Table 1 Basic equipment data

表2 能源基础数据Table 2 Basic energy data

表3 电网电力分时电价Table 3 TOU price of grid power

3.2 典型村能源系统容量配置方案与运行优化结果分析

3.2.1能源设备容量配置方案

根据多目标优化结果，选择总成本最优的粒子作为方案一，总碳排放量最低的粒子作为方案二，新能源消纳率最高的粒子作为方案三。将3个方案的计算结果列于表4。

表4 3方案对比Table 4 Comparison of three schemes

从表4可以看出，与未经优化前相比，3种容量配置条件平均可降低成本79.7%，降低碳排放量83.1%。对比方案一和方案二的碳排放量可以看出，风、光设备容量增大后减碳效果明显，与此同时会带来较高的装机成本。选取适当的新能源建设容量可以实现新能源的合理消纳，消纳率还与储能和其他能源的联动出力有关，增加新能源消纳率的同时会增加一定的运行成本。根据不同的目标需求，可以选择不同的设备容量配置方案。

3.2.2能源系统容量配置与运行优化结果

为了对优化结果进行整体分析，将pareto前沿结果绘制为曲面图(图4）。

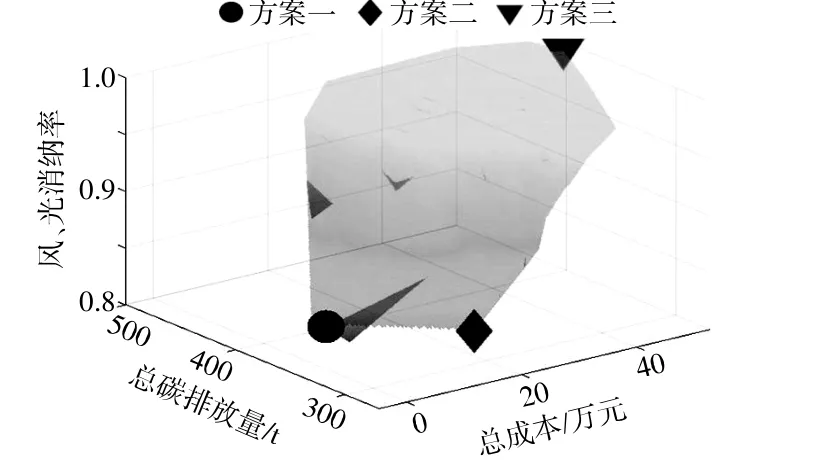
图4 Pareto最优前沿Fig.4 Pareto optimal frontier

在pareto前沿解集中，年总成本为-4.9～53万元，年碳排放量为268～460 t，风、光消纳率为83%～99%。从图4中还可以看出，碳排放量、总成本和消纳率之间呈现互斥关系，要优化其中一个目标值则必然要牺牲至少另外一个目标值。

3.2.3能源系统运行优化结果

为分析容量配置优化模型与运行调度优化模型之间的耦合关系，将3种方案下的设备运行优化结果绘成图5。

图5 3个方案能源系统运行出力Fig.5 Energy system operation output of the three schemes

图5中，存在储能设备同时充放电以及同时向电网购售电的数据点，这是因为图5是由5个运行场景中各设备出力计算得到，而不同场景间存在不同的充放电和购售电策略。从3种方案下的能源系统各设备出力情况可以看出，在追求经济性的方案一配置条件下，CF运行出力较高，系统向电网售电较多，购电较少，该配置和运行策略使得系统整体的经济性达到最佳；在追求低碳性的方案二配置条件下，系统使用煤炭和购电较少，使用风、光和生物质能源较多，该策略使得系统整体碳排放量最低；在方案三中，系统配置了较大容量的储能设备，并且在运行阶段储能设备频繁充放电，在合理的风力、光伏发电设备配置条件下，系统的风、光能源消纳能力达到最优。

3.3 确定性和随机性模型优化结果对比分析

为分析不确定性对系统容量配置结果的影响，分别对随机性和确定性条件下的模型进行优化，将pareto前沿中的设备容量以及目标函数结果取平均值进行对比，结果如图6和表5所示。

表5 随机性与确定性模型优化结果对比Table 5 Comparison of stochastic and deterministic objective functions

图6 随机性与确定性模型设备容量规划结果对比Fig.6 Comparison of random and deterministic device capacities

由图6可见，在相同条件下，随机性会使得EES，CF，HP以及BB的规划容量上升，PV容量下降，这是因为在随机性条件下，系统须要在风、光出力最低情况下保证能源供应，势必导致能源设备规划容量提高。这说明在考虑新能源出力随机性的情况下，系统需要更多容量的能源设备来平抑风、光发电的波动性，同时降低PV容量，以保证新能源的消纳率。

从表5中可以看出，与确定性模型优化结果相比，随机性主要影响了建设和运行阶段的成本，而对碳排放量和新能源消纳率的影响较小。这说明随机性的存在使得系统向电网售电减少，系统所需的设备冗余增加。此外，随机性条件下需多种能源配合运行来保证新能源的消纳，这造成碳排放量的增加。随机性对新能源消纳率的影响较小，说明该模型所采取的优化策略对风、光随机出力有较好的消纳效果。