基于改进局部极化准则的多核SVM模型

梁盛楠,刘文博,李雅芝

(1.黔南民族师范学院数学与统计学院,贵州 都匀 558000;2.黔南民族师范学院贵州省高等学校复杂系统与智能优化重点实验室,贵州 都匀 558000)

0 引言

20世纪90年代,Vapnik系统介绍了统计学习理论,同时提出了SVM算法[1].由于该算法在文本挖掘领域的出色表现[2],逐渐成为机器学习中的主流技术.SVM算法取得的巨大成功正式拉开了核方法研究的序幕,并促进了核方法的普及与应用,使其逐步扩展到机器学习的诸多领域,如模式识别[3]、特征选择[4]等.核函数直接决定了SVM分类算法性能的优劣,因为一个恰当的核函数可以将样本映射到一个合适的特征空间,使得同类样本之间紧密而异类样本之间分散.

由于不同核函数具有不同特性,因此在不同的应用场景,核函数所表现出的性能差别也较大.为了提升核函数的灵活性、适用性,将多个核函数进行核组合,即多核学习受到越来越多学者的关注.Yang等[5]提出多核学习支持向量机粒子群优化模型对肺结节进行识别,获得了更好的识别效率.高巍等[6]提出了一种用于高光谱图像分类的马氏距离多核学习方法,将马氏基本核进行线性加权组合,将高光谱数据映射到一个类内距离更小、类间距离更大的特征空间后进行分类.Gone等[7]将典型的多核学习算法进行分类总结,通过理论与实验分析得出多核学习可以提高预测精度、降低训练时间.上述研究工作已经证明利用多核替代单核可以增强决策函数的可解释性,使学习器获取更优的性能.

针对基本核函数的构造与多核学习中权系数的求解问题,本文提出基于改进核极化准则的多核SVM模型.受柯西密度函数启发,构造了广义p-范数柯西核,并给出理论证明;依据局部核极化准则重新定义关联系数,建立权系数与核参数优化目标函数,利用局部梯度与广义拉格朗日乘子算法进行求解,将构造的核函数进行核组合用于SVM分类预测;实验分析表明,与传统单核函数相比,本文提出的多核SVM模型在多数情况下其性能表现更好.

1 多核SVM模型

支持向量机(Support Vector Machine,SVM)是基于“结构风险最小化原则”面向二分类问题的判别分类算法,也可推广到多类分类问题中.它的基本模型是定义在特征空间上的间隔最大线性分类器,由于核函数的引入,使其实质上成为非线性分类器.

给定训练集T={(xi,yi)|xi∈p,yi∈{+1,-1},i=1,…,n}.其中:n表示样本容量,xi表示具有p个特征的输入向量,yi表示对应于xi的类别标签.SVM可形式化为如下凸二次规划问题:

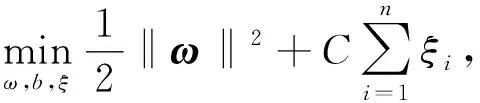
(1)

其中:ω表示分类超平面的法向量,决定了方向;b为位移项,决定了超平面与原点的距离;C是惩罚系数,C越大意味着误分类产生的代价越高;ξi表示松弛变量,度量了真实值yi与SVM预测值之间的距离.SVM的目标就是要最大化间隔2/‖ω‖.

基于核技巧的SVM是通过非线性映射φ(x),将样本从原始空间映射到一个高维特征空间中,使得样本在该特征空间中线性可分.φ(x)的形式往往未知,引入形式已知的核函数[8]代替复杂的内积运算,即κ(xi,xj)=φ(xi)·φ(xj).

在求解SVM的过程中,一般用到模型(1)的对偶形式

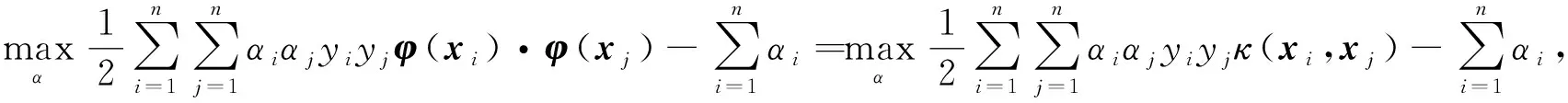
(2)

b依据训练集中的支持向量可被求解,形式为

其中:xs为支持向量,n′为支持向量的个数.

最终的分类超平面或SVM分类器为

由于不同的核适用领域不尽相同,为了将不同核函数的优势进行集成,最为直接的想法就是将多个不同的单核进行组合,基本形式为

(3)

(4)

2 广义p-范数柯西核

SVM的性能表现绝大程度上取决于核函数与核参数的选取,这就需要尝试构造新类型的核函数,使得SVM可适用于不同领域的数据分析.受到柯西概率密度函数的启发,本节将构造广义柯西核函数并将其扩展为广义p-范数柯西核.

柯西概率密度函数为

(5)

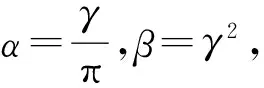
(6)

其中x,α,β>0.那么(6)式能否作为核函数,可由定理1—2给出.

定理1[9]若X⊂n,f：(0,∞)→,κ是X×X上的函数且κ(x,z)=f(‖x-z‖2),则当f完全单调时,κ(x,z)是正定核.

定理2 当α>0,β>0时,(6)式为核函数,其中x>0.

证明对(6)式求n阶导数可得

f′(x)=-α(x+β)-2,…,f(n)(x)=(-1)nα(x+β)-(n+1),

由于α>0,β>0,有

(-1)nf(n)(x)=(-1)2nα(x+β)-(n+1)=α(x+β)-(n+1)≥0.

因此f(x)完全单调,根据定理1可得(6)式为核函数.

将核函数(6)式推广为如下形式:

(7)

需要考虑参数v满足什么条件可以使上式成为核函数.

定理3 当α>0,β>0,ν>0时,(7)式为核函数,其中x>0.

证明对(7)式求n阶导数可得

f(n)(x)=(-1)nανv(v+1)…(v+(n-1))(x+β)-(v+n),

(-1)nf(n)(x)=(-1)2nανv(v+1)…(v+(n-1))(x+β)-(v+n).

若保证(-1)nf(n)(x)≥0,则需ν≥0.

依据定理1,当α>0,β>0,ν>0时,f(x)完全单调,所以f(x)=(α/(x+β))ν为核函数.

在具体的应用中,(7)式取如下形式:

(8)

(8)式称为具有p-范数距离形式的广义柯西核函数,简称广义p-范数柯西核.

3 核权重与核参数优化

本文依据核匹配准则,建立优化模型对核权重、核参数进行求解.该方法只依赖于训练样本且与后续分类器无关,因此该策略因实现简单而被广为使用.

3.1 核匹配准则

对核权重进行优化,其关键在于建立一个合理的目标函数.本文依据核匹配准则建立优化权重的目标函数.核匹配准则是基于矩阵匹配原理建立的参数优化准则,其基本原理如下:

给定训练集T={(xi,yi)|xi∈p,yi∈{1,2,…,l}}.核矩阵Κ=(κ(xi,xj))n×n,令Y=yyT=(yij)n×n为类标签矩阵,也称为理想核矩阵:

核匹配准则的目标就是要使得核矩阵与理想核矩阵之间的余弦相似度达到最大,其表达式如下:

(9)

其中:〈·,·〉F为Frobenius内积,‖·‖F为Frobenius范数.文献[10]证明了核匹配准则的可靠性、实用性以及核分类器泛化误差的有界性.在(9)式的基础上,Baram[11]提出了核极化准则(Kernel Polarization,KP):

(10)

核极化准则仅考虑了类间的可分离性而忽视了类内局部结构,Wang等[12]提出了局部核极化准则(Local Kernel Polarization,LKP):

(11)

定义关联系数Aij为

其中t>0为调节参数.

3.2 核权重与核参数优化

依据LKP的基本思想,构建改进的局部核极化准则模型以获取最优的核权重与核参数,改进部分体现在对LKP中的关联系数进行重新定义,具体的优化模型如下:

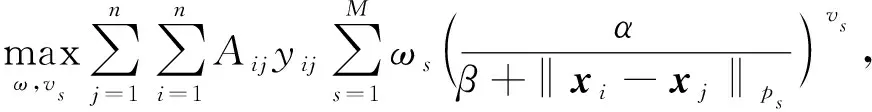
(12)

重新定义关联系数,以更好地刻画任意两个样本之间的相关程度:

(13)

对模型(12)的求解采用局部梯度与广义拉格朗日乘子相结合的优化算法[13-14],模型的梯度形式如下:

3.3 多核SVM分类模型计算过程

依据广义p-范数柯西核构造原理以及多核模型的建立与求解过程,加权广义p-范数柯西核SVM分类算法的基本流程如下:

输入:训练样本集Ttrain={(xi,yi)|xi∈p,yi∈Y,i=1,2,…,n},其中Y={1,2,…,l}表示类别标签;

步骤1:将原始数据集进行折交叉分层抽样,将其划分为训练集Ttrain与测试集Ttest;

步骤2:依据(3)式选取具体的核函数;

步骤3:依据(13)式建立关联系数矩阵;

步骤4:依据(12)式建立核权重与和参数优化的目标函数;

步骤5:基于训练集利用具体的优化算法对模型(12)进行求解,获取最优的权重系数ωi与核参数;

步骤6:将步骤5中得到的最优核权重与核参数带入到(3)式中;

步骤7:将步骤6中得到的(3)式带入到模型(4),得到具体的多核SVM的对偶基本型;

步骤8:利用分层抽样得到的训练集Ttrain对模型(4)进行拟合;

4 实验结果与分析

4.1 实验设定

为了验证本文构造的加权广义p-范数柯西核(Weight Generalizedp-Norm Cauchy Kernel,WGpCK)对SVM分类性能的影响,将其与多个传统的单核函数进行对比,包括多项式核(Polynomial Kernel,PolyK)、双曲正切核(Sigmoid Kernel,SigK)、高斯核(Gaussian Kernel,GauK)与拉普拉斯核(Laplace Kernel,LapK).本文提出的算法和实验基于R语言(版本号:3.6.3)编码实现.实验数据包括:慢性肾病(Kidney)、皮肤病(Dermatology)、皮马族糖尿病(Pima)、结肠癌(Colon)和乳腺癌(Breast)基因表达数据集,信息见表1.

表1 数据集信息

为了比较不同核函数对SVM分类性能的影响,实验采用5折交叉验证划分训练集与测试集,评价准则采用分类精度、Kappa系数.将不同的核SVM方法分别记为PolyK+SVM、SigK+SVM、GauK+SVM、LapK+SVM和WGpCK+SVM.

4.2 对比实验

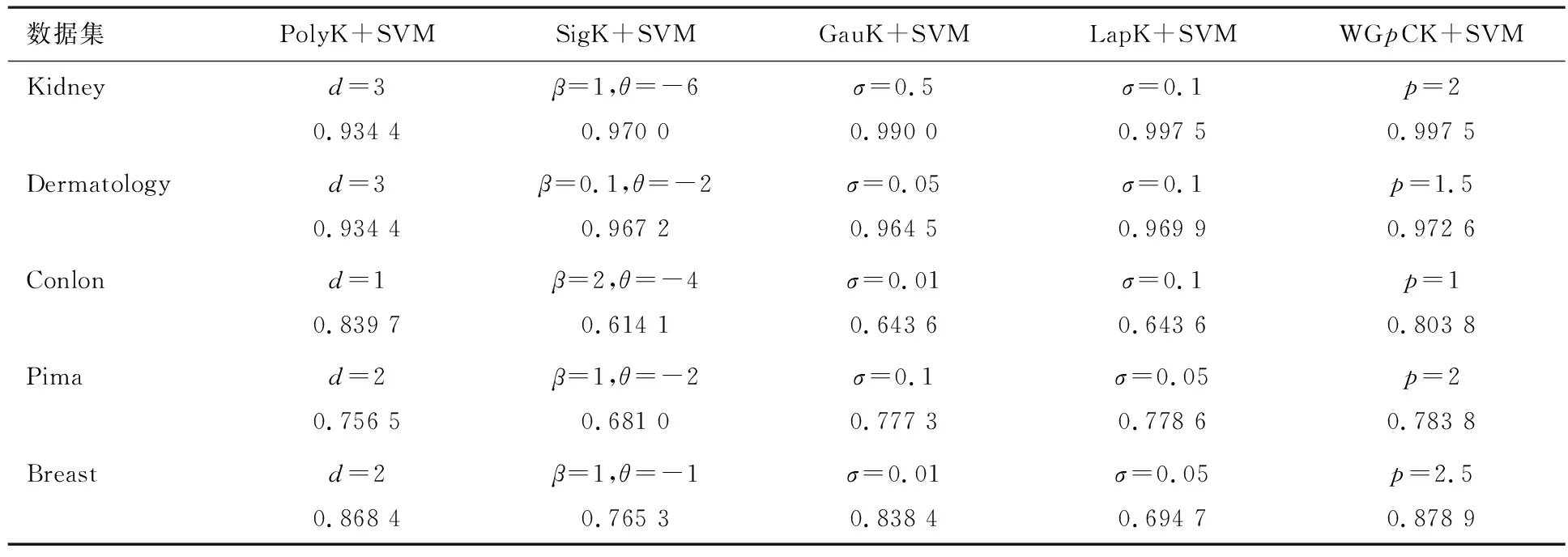
表2 基于不同核函数的SVM算法5折交叉验证分类精度

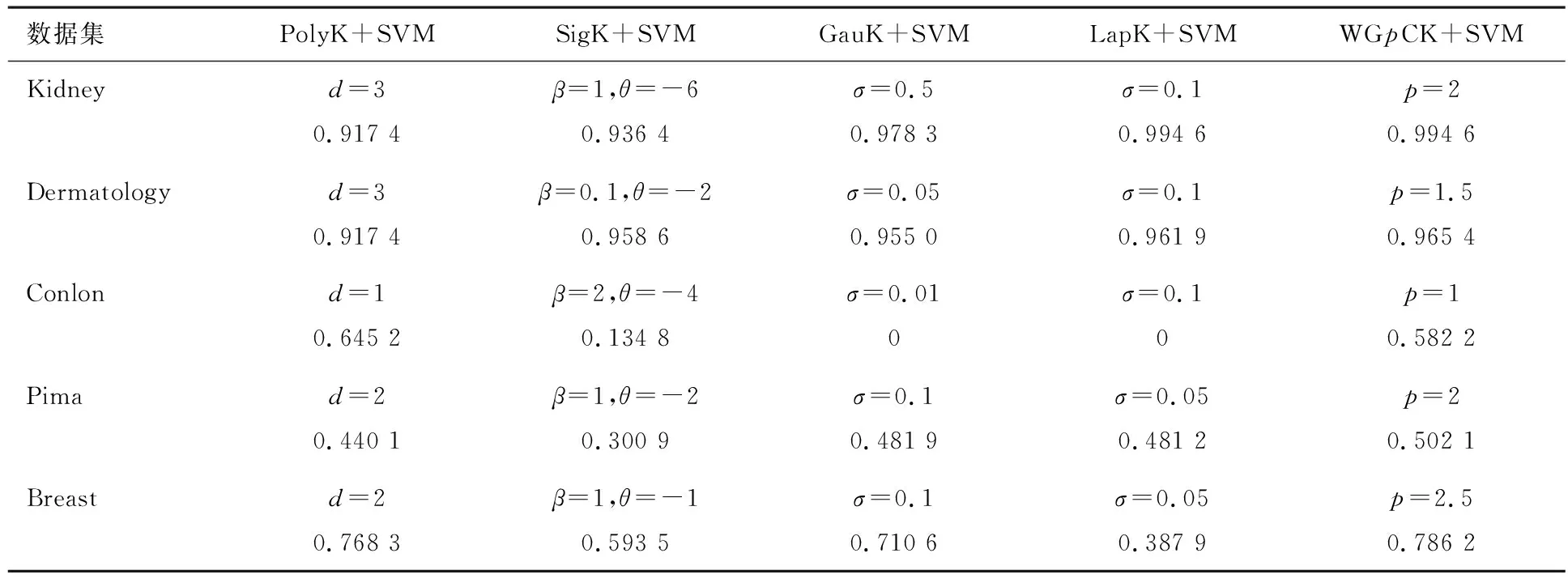
表3 基于不同核函数的SVM算法5折交叉验证分类Kappa系数

通过表2—3的实验结果可知,将广义p-范数柯西核进行加权组合,将其应用于SVM算法对5个真实数据集进行分类预测时,WGpCK+SVM算法在精度上有4处达到最优,1处达到次最优;在Kappa系数上有4处达到最优,1处达到次最优.在分析的5个数据集上,WGpCK+SVM有8处达到最优,2处达到次最优,表明本文构造的广义p-范数柯西核,在多数情形下可以有效提高SVM算法的分类预测性能.

4.3 p-范数距离显著性分析

对于WGpCK +SVM算法,当面对不同的数据集时设定了不同的p-范数距离,因为在实验分析的过程中发现,在广义p-范数柯西核中取定不同的范数会影响到SVM算法的分类性能,具体情况见图1,其中p的取值范围设置成[1,50]步长为0.5.

从图1中可以明显地看出,Colon、Kidney和Pima数据集的精度、Kappa系数都随着p-范数距离的增加呈现出较为显著的变化.对于Pima与Kidney数据集,其2个评价指标值逐渐增加到一个最高点,然后总体呈下降趋势,中间略有波动,最后趋于平稳.对于Colon数据集,其3个评价指标值随p-范数变化呈现出明显的随机波动趋势.对于Breast数据集,其精度和Kappa系数达到最高点后开始下降并基本维持在一个水平上.对于Dermatology数据集,其评价指标值只是随p-范数变化产生了微小的波动.从图1的可视化结果可以得出,设定不同的p-范数距离在有些数据集上对分类算法性能产生了显著影响,而在有些数据集上影响不显著.

5 结论

依据柯西概率密度函数,本文构造了广义p-范数柯西核.将核函数进行加权组合,依据局部核匹配准则,建立优化模型对权系数、核参数进行求解.将最终得到的多核模型应用于SVM分类,通过在5个医学数据集上的实验分析,与传统的单核相比,本文提出的多核SVM模型具有更好的分类预测性能,这对正确识别正常人群与患病人群、不同类型癌症基因有着重要应用价值.通过可视化分析了p-范数距离对WGpCK+SVM算法预测性能的影响,得出针对不同的数据集,不同的范数距离会对算法性能产生不同的影响效果,有的影响显著,有的影响微小.在未来的工作中,可以将提出的多核SVM模型应用于金融、经济等领域,如股票收益率预报、企业信用评级等.