无记忆状态反馈广义H2控制
2023-12-21孙凤琪
孙 凤 琪
(吉林师范大学数学学院,吉林 四平 136000)
0 引言
广义控制理论的提出,有效地改善了由鲁棒性引起的系统性能衰竭与不稳定等现象,使系统具有了更好的动态稳态性能和稳定奇异摄动区间.记忆控制在外部干扰输入变化不大的情况下效果良好,但当干扰信号复杂且频繁变化时,就很难达到预期控制目的,此时无记忆控制就显示出其控制方法的优越性.
近年来,广义H2控制问题已成为自动控制理论及工程应用研究的热门课题之一,在诸多学者的共同努力下,已形成了比较完善的理论体系.[1-3]
文献[4]针对一类含有马尔可夫跳变参数和时滞的广义系统的L2-L∞控制问题,提出一种基于模态跳变的无记忆状态反馈控制器的构造方法.其通过反证法、线性变换技巧以及矩阵分块技术,将含有马尔可夫跳变参数广义系统的正则性转化为系统矩阵不等式的可解性问题,给出一个新的控制器的设计方法.但矩阵分块技术的引入带来了计算复杂度的增加.文献[5]研究了时滞系统的非脆弱广义H2控制问题.设计了无记忆的状态反馈控制器,使得对于所允许的不确定性,对应的闭环系统是稳定的,同时具有固定的广义H2性能指标.利用线性矩阵不等式技术,得出时滞系统存在非脆弱广义H2控制器的充分性条件.然而,在奇异摄动不确定性时的条件并没有提及,系统存在单一性.
本文在记忆状态反馈广义H2控制器存在的理论基础上[6],以Lyapunov稳定性定理、线性矩阵不等式方法以及交叉项界定方法为基础,讨论了系统广义H2镇定方法.选取新的依赖于时滞和摄动参数的二次型李雅普诺夫泛函,同时借助新的引理及交叉项界定方法,推出了在时滞依赖和时滞独立2种情形下的无记忆广义H2控制充分性的判据.
考虑如下系统:
(1)
设计无记忆状态反馈控制器为
u(t)=Kx(t),
(2)
其中K是待定的控制器增益矩阵,则闭环系统为
(3)
其中
1 判定定理
以下结论中的时滞和不确定性满足文献[6]中的条件(2)—(3),当矩阵不等式条件(6)—(8)成立时,可得如下时滞依赖情形下的无记忆状态反馈广义H2控制定理:

其中:
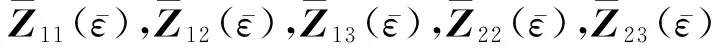
类似文献[6]中定理1,可构造新的Lyapunov-Krasovskii泛函:
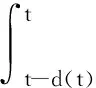
其中Q,M为对称正定矩阵,即Q>0,M>0,从而V(x(t))正定.
显然,定理1的矩阵不等式条件对于变量Q,M,P,K和Z(ε)是非线性的,对定理1进行线性化,可得如下结果:

其中:
Φ12(0)=AdZ(0),
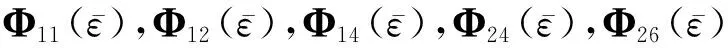

其中
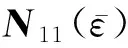
2 推论
若去掉系统(1)中的不确定性矩阵F(t),则系统成为
(4)
其中系统矩阵等均与系统(1)相同,则闭环系统成为
(5)
其中:
由定理2得如下线性化推论.

其中:
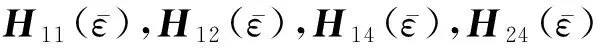
若去掉系统(1)中的时变时滞可微函数d(t),则系统成为
(6)
其中系统矩阵等均与系统(1)相同,则闭环系统为
(7)
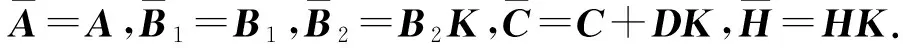

其中:
类似地,对于时滞独立情形,若去掉系统(1)中的控制输入u(t)和干扰输入ω(t),则系统成为
其中系统矩阵等均与系统(1)相同,则可推出新的推论,此处略去.
3 算例
考虑如下带有控制输入和干扰输入的时变时滞不确定控制系统:
令

δ1=1.031 3,δ2=3.915 0,η1=1.439 0,η2=4.755 0,η3=2.884 0,
Z1=1.578 9,Z2=-7.015 0,Z3=6.380 1,Z4=3.708 6,Z5=3.252 2.


表1 广义H2稳定性能指标对比
由表1可见,定理2所设计的控制器有较大的奇异摄动参数上界值0.35,同时广义H2控制区间在(0,0.35]内,大于文献[7]的(0,0.3],扩大了闭环系统的渐近稳定范围,最优L2-L∞性能指标1.320 1也相对较小.通过将本文所得定理的广义H2稳定的性能指标与相关文献对比,可见本文定理得到的控制器控制效果具有一定的优越性,并且适用于标准和非标准情形.

4 结论
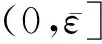
本文可为多时滞奇异摄动控制系统研究提供理论参考.如何将结论推广到输出反馈广义H2控制问题中、将连续奇异摄动系统拓展到离散奇异摄动系统[8],是进一步需要研究的问题;如何引入新的交叉项界定,使得即使结果具有一定的保守性,也能换取实际控制系统的可行性等[9-11],有待进一步探讨.
