关于矩阵的Schatten p-范数的注记
2023-12-21任芳国和嘉琪
任芳国,和嘉琪
(陕西师范大学数学与统计学院,陕西 西安 710119)
矩阵的Schattenp-范数是一类重要的矩阵范数.它具有良好的性质,如酉不变性质及单调性,因此矩阵Schattenp-范数在量子信息中刻画量子态之间的距离和保真度、熵和相对熵以及量子的纠缠度和相干度有重要作用[1].本文在文献[1-9]的基础上,讨论了矩阵Schattenp-范数与其主对角线元素及分块矩阵主对角块p-范数之间的关系,进而给出矩阵与其伴随换位子Schattenp-范数之间的关系,讨论了矩阵的绝对值、换位子2-范数的界,所得结果细化和深化了矩阵Schattenp-范数的已有结果.
1 预备知识
为讨论方便,引入以下定义和引理,其余未加说明的记号参见文献[2].
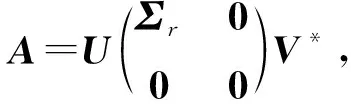

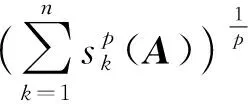
注1 ‖A‖1为A的迹范数,‖A‖2为A的Frobenius范数,‖A‖∞为A的谱范数.
定义3[4]设A∈Mn,称(A*A)1/2为A的绝对值,记作|A|.
引理1 设A,B∈Mn是半正定矩阵且tr(AB)=0,则AB=0.

引理2[4](Weyl单调定理) 设A是n阶Hermite矩阵,H是n阶半正定矩阵,则λj(A+H)≥λj(A),其中j=1,2,…,n.
2 主要结论
分别利用矩阵分解、矩阵分块的技巧及矩阵Schattenp-范数的特性,深入讨论矩阵Schattenp-范数的性质.
定理1 设A=(aij)n∈n×n,p≥1,则:
(1) Re(tr(A))=‖A‖1,当且仅当A是半正定矩阵;

(3) 设e1,…,en与f1,…,fn是n中两组标准正交基,则

(1) 必要性.由U1,V1是等距矩阵及柯西不等式有,
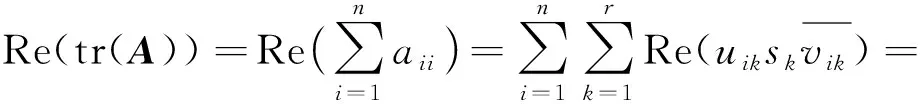
如果Re(tr(A))=‖A‖1,则由sk>0,k=1,…,r可知,



(2) 设f(x)=xp.由p≥1知,f(x)在[0,+∞]上为单调递增凸函数.由
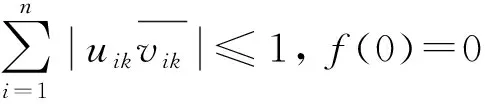

(3) 令
U=(e1,…,en),V=(f1,…,fn),
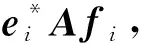
结论证毕.

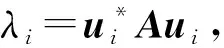

定理2 设p≥1,Pi∈n×n是一簇正交投影矩阵,其中i=1,…,m,有以下结论成立:
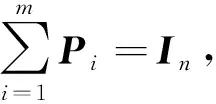
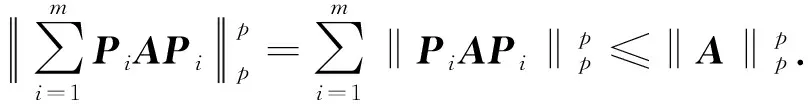
证明(1) 先证PiPj=δijPi.

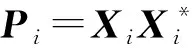
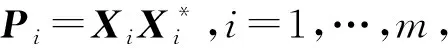


再证c(B)是B的酉相似凸组合.

设s=j-i,若εs≠1及(εs)m=1知,
那么
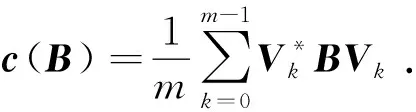
最后,由‖·‖P是酉不变范数知,

又
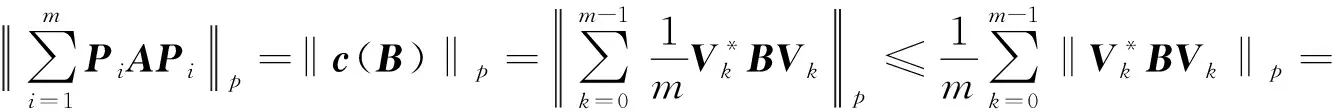
故
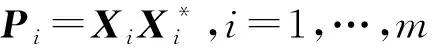
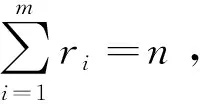
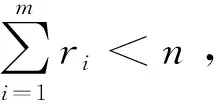
且
综上,定理得证.
定理3 设A∈Mn,p≥1,则:
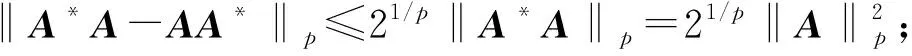
(2) ‖A*A-AA*‖p≥(2-21/p)‖A*A‖p-21/p‖A2‖p;

证明(1) 由于
则由引理2知,
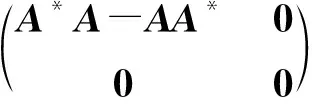
那么
‖A*A-AA*‖p≤21/p‖A*A‖p.
再由
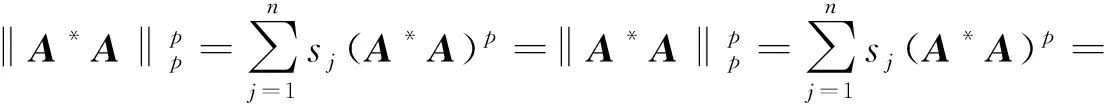
则结论(1)成立.
(2) 由于‖AA*‖p=‖A*A‖p,‖A2‖p=‖(A2)*‖p,则
于是
‖A*A-AA*‖p=‖2A*A-(A*A+AA*)‖p≥‖2A*A‖p-‖A*A+AA*‖p≥
2‖A*A‖p-(21/p‖AA*‖p+21/p‖A2‖p)=(2-21/p)‖A*A‖p-21/p‖A2‖p.
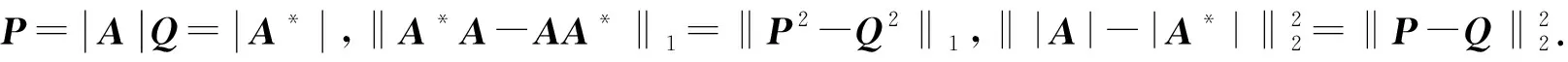


|P-Q|=(P-Q)V=V(P-Q).
设W=(w1,…,wn)为W的列分块矩阵,再由P2-Q2=1/2[(P+Q)(P-Q)+(P-Q)(P+Q)]知,

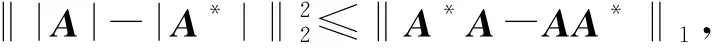
推论2 设A∈Mn,r=r(A),p≥1,则:


证明(1) 由矩阵的Frobenius范数的定义及向量的lp范数性质知,‖A*A-AA*‖1≤r1-1/p‖A*A-AA*‖p,即有
r1/p-1‖A*A-AA*‖1≤‖A*A-AA*‖p,
再由定理3结论(3)知,
定理4 设A∈Mn是正规矩阵,X∈Mn,则:
(1) ‖AX-XA‖2=‖A*X-XA*‖2;
(2) ‖|A|X-X|A|‖2≤‖AX-XA‖2.

设U*XU=(xij)n,由Frobenius范数的酉不变性可知
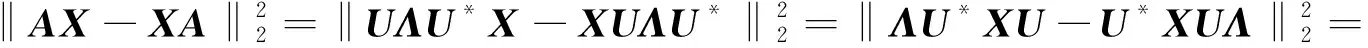
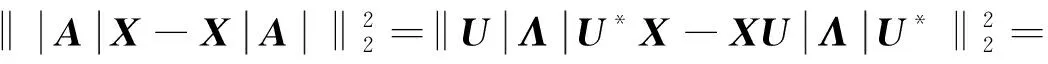
推论3 设A,B∈Mn是正规矩阵,X∈Mn,则‖|A|X-X|B|‖2≤‖AX-XB‖2.
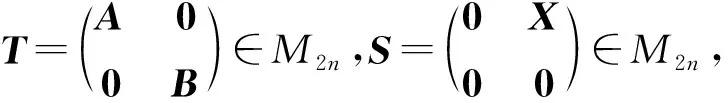

由
再结合定理4结论(2)有
‖|T|S-S|T|‖2≤‖TS-ST‖2.
即
那么‖|A|X-X|B|‖2≤‖AX-XB‖2.
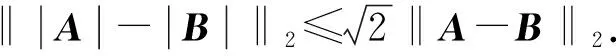
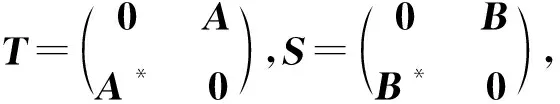
于是由推论3有
即

3 总结
本文主要利用矩阵奇异值分解、谱分解、柯西不等式、分块矩阵的主对角块组成的准对角矩阵可以表示成其凸组合、正交投影、正规矩阵及Schattenp-范数的特性,深入讨论了矩阵主对角线元素与矩阵Schattenp-范数之间的关系,刻画了分块矩阵与其主对角块p-范数之间的关系,深入研究了矩阵与其伴随换位子Schattenp-范数之间的关系,给出了矩阵的绝对值及换位子之间Frobenius范数的界,所得结果细化和深化的矩阵Schattenp-范数的已有结果,这使我们更加了解Schattenp-范数的性质以及为解决其量子信息数值问题奠定了基础.
