基于标准化降雨实际蒸散指数的重庆干旱预测模型构建

2023-12-21李遥

水利规划与设计 2023年12期

李遥

(重庆市水利电力建筑勘测设计研究院有限公司，重庆 401121)

0 引言

随着全球变暖现象的持续发生，干旱在区域的发生频率呈现逐年升高的趋势，干旱已成为了限制区域发展的重要因素之一[1-2]。为表征区域干旱发生规律，选择合适的干旱评价指标，构建区域高精度干旱预测模型是进行干旱监测和预警的基础。

干旱指标可定量评价区域干旱等级，对研究区域干旱分布规律十分重要。目前，应用最广泛的干旱指标主要包括相对湿润指数MI[3]、标准化降水指数SPI[4]、标准化降雨蒸散指数SPEI[5]等。其中SPEI指数充分考虑了区域降水和潜在蒸散发的关系，能够更好表征区域干旱，逐渐表现出了较高的适用性[6]。但SPEI指数的潜在蒸散发未考虑下垫面情况，因此众多学者探究了新型干旱指数，采用实际蒸散发代替潜在蒸散发，构建标准化降雨实际蒸散指数SPAEI衡量区域干旱。

由于影响区域干旱的因素较多，构建传统数学模型用于预测干旱较为困难，采用机器学习技术是目前的研究趋势。殷浩等[7]基于机器学习模型构建了季尺度干旱预测模型，指明机器学习技术在干旱预测中具有较大的潜力；赵国羊等[8]基于神经网络和支持向量机模型进行了干旱预测，并得到了区域干旱预测精度最高模型。本文以双向长短期记忆神经网络模型(BiLSTM)为基础，基于布谷鸟算法(CS)、孔雀算法(POA)、麻雀搜索算法(SSA)、野狗算法(CAP)、蝙蝠算法(BA)共5种新型智能算法进一步优化BiLSTM模型，构建区域新型干旱预测模型。

较严重的季节性干旱在一定程度上限制了区域发展。本文选择了重庆市1963-2018年9个站点的逐日气象数据，数据均来自国家气象中心，质量控制良好。

1 研究方法

1.1 标准化降雨实际蒸散指数

采用实际蒸散发代替潜在蒸散发，得出SPAEI指数，具体步骤为：

(1)计算水分亏缺量

采用降雨与实际蒸散的差值，表示不同站点水分亏缺量的大小。其中，实际蒸散采用最大熵增蒸散模型计算[9]。水分亏缺量的公式为：

Di=Pi-AETi

(1)

式中，Di-第i个月的水分亏缺量，mm；Pi-第i个月的累积降雨量，mm；AETi-第i个月的累积实际蒸散发，mm。

(2)标准化处理

选择合适的分布函数对算出的Di值进行标准化处理，以消除数据计算过程中的不确定性。

(3)计算SPAEI指数

根据下式计算SPAEI指数，具体公式为：

(2)

(3)

式中，P-超过特定值的概率；C0、C1、C2、d1、d2、d3-经验常数。

1.2 预测模型构建

(1)长短期记忆神经网络模型

本文基于长短期记忆神经网络模型LSTM构建区域干旱预测模型。该模型是一种引入时间序列的深度学习模型，在模型中包括了遗忘阀门、输入阀门、更新阀门和输出阀门来实现个体寻优，具体步骤可见文献[10]。

(2)双向长短期记忆神经网络模型

双向长短期记忆神经网络模型BiLSTM是在传统的LSTM模型基础上，增加了反向学习功能，可进一步提高模型预测精度。

(3)布谷鸟优化算法

Yang和Deb[11]基于布谷鸟觅食行为构建了布谷鸟优化算法CS，通过布谷鸟幼崽模仿成熟群体的觅食行为，实现个体位置的最优化处理。

(4)孔雀优化算法

Wang等[12]基于孔雀求偶、觅食的行为构建了孔雀优化算法POA，算法中将个体群分为了雌、雄、幼年孔雀三大类，通过模拟雄孔雀求偶、雌孔雀接近和幼年孔雀觅食的行为实现位置最优化计算。

(5)麻雀搜索算法

Xue等[13]基于麻雀觅食行为构建了麻雀搜索算法SSA，该算法中将参数寻优过程分为了发现、跟随和侦察三大列，实现输入结果的最优化处理。

(6)野狗算法

Pezara-Vazquez等[14]基于澳大利亚野狗的狩猎行为提出了野狗优化算法DOA。该算法通过模拟野狗在狩猎过程中的群攻、独自狩猎和随机狩猎模式，实现算法寻优。

(7)蝙蝠算法

Yang等[15]基于蝙蝠回声原理构建了蝙蝠优化算法BA，该算法通过蝙蝠回声定位，实现个体位置及运动方向的更新。

1.3 模型评价

以BiLSTM模型为基础，基于5种优化算法构建5种优化BiLSTM模型，并将5种模型模拟结果与LSTM模型、随机森林模型(RF)和广义回归神经网络模型(GRNN)进行对比，选出精度最高模型，模型精度选择相对误差RE、相对均方根误差RRMSE、模型效率系数Ens和决定系数R2来进行综合评价。

2 结果与分析

2.1 模拟结果时间趋势对比

图1绘制了不同模型模拟结果与SPAEI标准值的变化趋势对比。在图1中可知，SPAEI值在年内呈现出了一定的周期性变化规律，模型模拟值的变化趋势与标准值均一致。在所有模型中，优化模型的模拟结果显著优于传统未优化模型。POA-BiLSTM模型模拟值变化趋势与标准值最为接近，SSA-BiLSTM模型精度次之，优化模型中BA-BiLSTM模型精度较低。传统模型中，BiLSTM模型和LSTM模型的变化趋势拟合效果优于RF模型和GRNN模型。

图1 不同模型模拟结果时间变化趋势对比

2.2 模拟精度对比

通过计算不同尺度下不同模型模拟SPAEI值的模拟精度，绘制了不同尺度模拟精度箱线图，结果如图2-6所示。图2为模拟的春季SPAEI值精度对比。在图2中可知，优化模型的精度优于传统模型，POA-BiLSTM模型精度最高，该模型的Ens和R2中位数分别为0.982和0.980，RE和RRMSE的中位数仅为2.596%和10.043%；SSA-BiLSTM模型精度次之，该模型的Ens和R2中位数分别为0.962和0.950，RE和RRMSE的中位数为4.207%和11.745%；优化模型中，BA-BiLSTM模型的精度较低，Ens和R2中位数分别为0.900和0.897，RE和RRMSE的中位数为8.129%和17.465%；传统模型中，GRNN模型精度较低。

图2 SPAEI春季模拟精度对比

图3为模拟的夏季SPAEI值精度对比。在图3中可知，优化模型的精度优于传统模型，POA-BiLSTM模型精度最高，该模型的Ens和R2中位数分别为0.987和0.982，RE和RRMSE的中位数仅为7.373%和7.097%；SSA-BiLSTM模型精度次之，该模型的Ens和R2中位数分别为0.963和0.961，RE和RRMSE的中位数为9.007%和9.020%；优化模型中，BA-BiLSTM模型的精度较低，Ens和R2中位数分别为0.884和0.921，RE和RRMSE的中位数为14.584%和14.406%；传统模型中，GRNN模型精度较低。

图3 SPAEI夏季模拟精度对比

图4为模拟的秋季SPAEI值精度对比。在图4中可知，优化模型的精度优于传统模型，POA-BiLSTM模型精度最高，该模型的Ens和R2中位数分别为0.983和0.981，RE和RRMSE的中位数仅为1.882%和2.182%；SSA-BiLSTM模型精度次之，该模型的Ens和R2中位数分别为0.963和0.958，RE和RRMSE的中位数为5.784%和4.152%；优化模型中，BA-BiLSTM模型的精度较低，Ens和R2中位数分别为0.903和0.883，RE和RRMSE的中位数为10.216%和9.593%；传统模型中，GRNN模型精度较低。

图4 SPAEI秋季模拟精度对比

图5为模拟的冬季SPAEI值精度对比。在图5中可知，优化模型的精度优于传统模型，POA-BiLSTM模型精度最高，该模型的Ens和R2中位数分别为0.972和0.973，RE和RRMSE的中位数仅为4.996%和4.856%；SSA-BiLSTM模型精度次之，该模型的Ens和R2中位数分别为0.949和0.953，RE和RRMSE的中位数为6.442%和6.352%；优化模型中，BA-BiLSTM模型的精度较低，Ens和R2中位数分别为0.823和0.888，RE和RRMSE的中位数为12.708%和12.453%；传统模型中，GRNN模型精度较低。

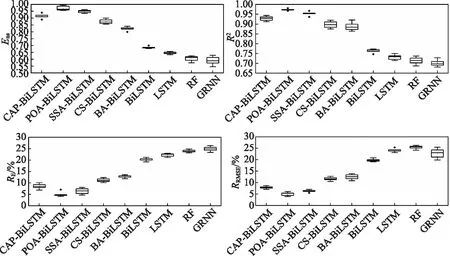
图5 SPAEI冬季模拟精度对比

图6为模拟的全年SPAEI值精度对比。在图6中可知，优化模型的精度优于传统模型，POA-BiLSTM模型精度最高，该模型的Ens和R2中位数分别为0.926和0.935，RE和RRMSE的中位数仅为8.680%和9.209%；SSA-BiLSTM模型精度次之，该模型的Ens和R2中位数分别为0.910和0.921，RE和RRMSE的中位数为11.620%和14.453%；优化模型中，BA-BiLSTM模型的精度较低，Ens和R2中位数分别为0.870和0.866，RE和RRMSE的中位数为18.240%和21.234%；传统模型中，GRNN模型精度较低。