基于改进无参数K-means算法的刀具状态分析
2023-12-21吴晓勇侯秋丰
吴晓勇,侯秋丰,罗 勇
(浙江向隆机械有限公司 产品开发部,浙江 宁波 315311)
0 引 言
K-means算法具有简洁、收敛速度快、处理大规模数据集时能延展伸缩等优点[1-4]。但在对数据进行聚类分析时,需要预先知道聚类数k,而对很多数据集,初始的聚类数k难以预知; 并且K-means初始的聚类中心随机选择,可能导致算法的聚类结果不够稳定,最后收敛于局部最优的情况。
针对上述问题,目前人们已经进行了许多改进。何洪磊[5]提出了一种基于密度峰值网格的K-means初始聚类中心优算法,其综合了网格分析的高效性和密度峰分析的准确性,在人工模拟数据集和UCI(University of California,Irvine)数据集上获得了比传统K-means和K-means++更好的聚类效果以及更快聚类速度。王海燕等[6]提出了Canopy+_K-means算法,从阈值获取方式和初始聚类中心的选取两方面进行了改进。Tunali等[7]提出一种多集群球形K均值算法,其允许在K-means聚类过程将一个样本点同时分配给多个集群,只要满足相似比率限制参数的指定条件,即可确定分配的最大集群数。Redmond等[8]提出一种采用kd-树确定K-means聚类中心的方法,通过kd-树获取数据的密度估计,然后使用距离和密度信息进行选择,依次选择k个聚类中心。Ismkhan[9]提出I-K-means-plus方法,该算法尝试在K-means算法每次迭代过程中删除一个簇,然后拆分另一个簇进行迭代,以此提高K-means的聚类精度,该方法以较小的额外时间成本为代价,提高了算法的精度。
为解决上述问题,笔者提出一种无参数K-means算法。首先,计算样本点的局部密度和离散度,然后建立决策图,将两个参数组成向量,计算每个点到周围点的距离,筛选出距离大于2倍均方差且密度大于平均密度的点作为算法的初始聚类中心,统计聚类中心个数k作为聚类个数,将初始聚类个数k以及初始聚类中心作为K-means算法的初始参数对数据进行聚类。对UCI数据集、人工建立的高斯数据集以及真实刀具振动数据集3种不同的数据集进行聚类,与传统K-means算法、FCM(FuzzyC-means)聚类算法和GKM(GlobalK-Means)算法聚类效果对比的结果表明,所提算法保持传统算法全局最优性,验证了笔者提出的算法具有有效性。此外,由于K-means是一种无监督聚类方法,在获得较优刀具状态识别结果的同时,可减少人工数据标定,有监督训练等工作量及运算成本,对准确实时提取数控机床刀具运行状态具有较高的实际意义。
1 算 法
1.1 K-means聚类算法
K-means算法是一种基于距离测量的聚类分析算法。该算法的聚类过程如下:首先输入聚类个数k,从待聚类的数据集中随机选取k个对象作为算法的初始聚类中心,然后计算选择的聚类中心和对象间的距离,将样本对象分配给距其最近的聚类中心。并且初始选定的聚类中心也会随着每个样本的分配而被重新选定。
算法的输入是一个无标记的数据集合{x(1),x(2),…,x(m)},因为这是无监督学习算法,所以在集合中只能看到x,没有类标记y。K-means聚类算法是将样本聚类成k个簇(Cluster),具体算法步骤如下:
Step 1 随机选取k个聚类质心点(Cluster Centroids),则等于存在了k个簇c(k):
μ1,μ2,…,μk∈Rn。
(1)
Step 2 对所有x(i),分别计算质心μj和x(i)的距离,x(i)是离其最近的质心μj的簇c(j):
(2)
Step 3 对每个类c(j),重新计算该簇质心的值:
(3)
重复Step2和Step3,直到算法收敛。
1.2 基于密度峰值聚类算法
Rodriguez等[10]通过快速搜索并找到密度峰值的聚类方法(CFSFDP:Clustering by Fast Search and Find of Density Peaks),算法计算2个参数:局部密度ρi和高密度点之间的距离δi,并根据这2个参数之间的关系建立决策图。
首先,需分别计算所有数据点i的局部密度ρi,以及与其余高密度点的距离δi,数据点间的距离dij决定了ρi,δi的值,上述数值满足三角不等式关系时,将ρi定义为
ρ(xi)={x|d(x,xi)≤dc},
(4)
其中d(x,xi)为其他数据点和xi的距离,dc为截止距离。通常,分布于数据点xi邻域范围内的点的个数作为xi的局部密度ρi,邻域的截止距离为dc,δi则表示点xi与其他高密度之间的最小距离:
(5)
对密度最大的数据点,δi用所有点之间的最大距离表示为
(6)
CFSFDP算法将相对较大的ρi、δi选为聚类中心,其他点被分到与它最近的聚类中心的类,较小的ρi、较大的δi的特征点看作噪声。
1.3 笔者算法
由于K-means算法无法确定聚类个数,且前期随机选取聚类中心易导致聚类结果陷入局部最优的问题,笔者结合CFSFDP算法得出自动确认聚类个数、中心的一种无参数K-means聚类算法。首先确定xi的邻域U(xi),U(xi)定义为
U(xi)={xj|xj∈X&dij≤dl}(i≠j),
(7)
其中dij=d(xi,xj)为样本点xi和xj之间的欧氏距离;dl为距离阈值,代表数据集X所有样本点之间欧氏距离的平均值的1/10,计算公式为
(8)
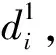
(9)
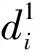
(10)
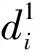
笔者以样本点xi与其他高密度点的距离衡量样本点xi与其他高密度点的离散程度,记为δi。通常,数据集中密度最大的数据点,可默认为一个聚类中心,计算该点与数据集X中所有点的最大距离; 对剩余的数据点,计算该点与其他高密度点之间的最小距离,公式为
(11)
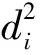
(12)
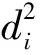
在计算了数据集中每个点的局部密度ρi和离散度δi后,将每个样本点归一化后的邻域密度和离散度组成一个向量(ρi,δi),并将ρi作为横坐标,δi作为纵坐标得到算法的决策图。此时,计算数据点xi与其最近邻的5个点的距离之和的均值:
(13)
将Di值按降序排列,筛选出Di值大于2倍均方差且局部密度大于数据集中所有点的平均密度的点,作为笔者算法筛选出的聚类中心,算法统计聚类中心的个数k作为待聚类数据集的类的个数。
在确定聚类中心值{c1,c2,…,ck}以及初始聚类数k后,将其作为K-mean算法的初始输入参数,实现对多类数据集的无参数聚类分析。对数据集X,将其中的每个样本分配到距离其最近的类中,并使误差函数J达到最小,则完成聚类,则有
(14)
其中N为样本数量,k为聚类个数,d(xi,cj)为数据集中第i个样本xi与第j个聚类中心cj之间的欧氏距离。
综上,笔者所提出的一种无参数K-means算法的实现步骤为:
Step 1 确定数据集中每个待聚类样本点xi的邻域U(xi),然后计算每个样本点的邻域密度ρi并归一化;
Step 2 计算样本点xi的离散度δi并归一化;
Step 3 将每个样本点归一化后的邻域密度和离散度组成一个向量,并以样本点的邻域密度ρi作为横坐标,离散度δi作为纵坐标绘制决策图;
Step 4 评估数据点xi是否为候选聚类中心,实现方法为计算该点与其最邻近5个点的距离之和的均值Di,将Di值降序排列,筛选出Di值大于2倍均方差、且局部密度大于数据集中所有点的平均密度的点作为初始聚类中心,记录聚类中心的个数k;
Step 5 将上一步得到的聚类中心点和聚类中心个数k作为K-means算法的聚类中心和聚类中心个数,对数据集进行聚类。
2 实 验
2.1 数据集选取
为验证笔者所提出的算法是否有效,对多个数据集进行了测试。测试过程中,选择模拟和真实数据集分别进行检验。图1为模拟数据集的空间分布形式,每个不同点的位置由不同坐标轴表示,不同数据集分别代表不同的数据分布类型。图1a包含了5个类的数据集,每个类之间点的聚类较近,不同类之间数据点之间的距离较远; 图1b包含了20个类的数据集,类的数量较多,其中包含彼此距离较近的类,也包含距离较远的类; 图1c数据集中包含了重叠数据集; 图1d数据集为不平衡数据集,不同数据类之间数量差别较大,分别为1 000,400,100。

图1 高斯数据集
使用仿生传感器对机床上的刀具振动情况进行采集后,得到振动数据集,将得到的振动数据集与UCI数据集结合组成本次实验所需的真实数据集,表1为真实数据集的相关信息。
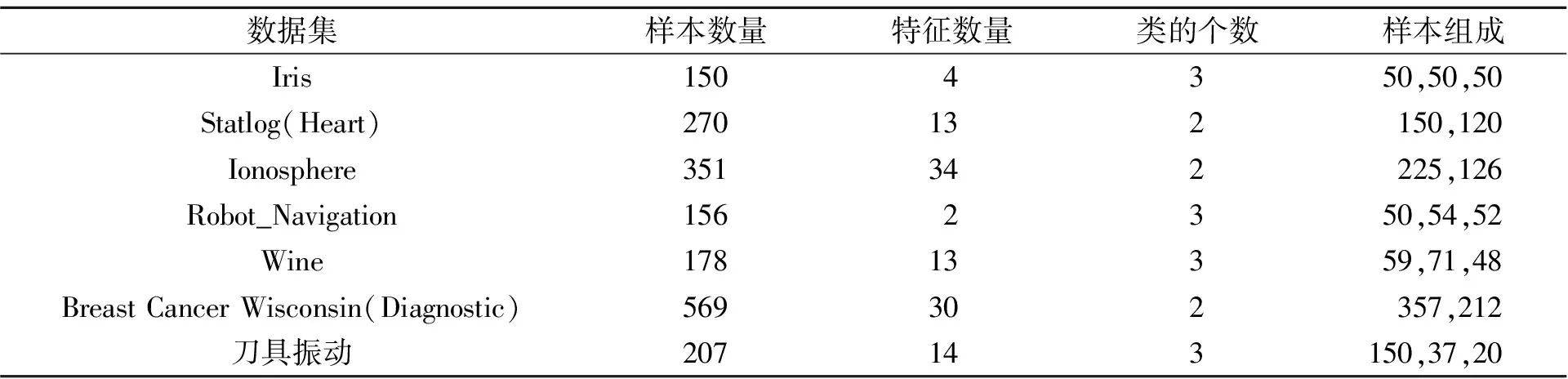
表1 真实数据集和UCI数据集信息
Iris数据集由3个不同类别的鸢尾花的特征组成,每个类的数量均为50个。其中有一类鸢尾花特征与其他两类线性可分,另外两类线性不可分。Statlog(Heart)数据集的样本特征表征了患者是否患有心脏疾病,共包含两类:有心脏病的类包含150个样本,没有心脏病的一类包含120个样本,每个样本包含13个特征。Ionosphere数据集为约翰霍普金斯大学电离层数据库,预测结果为良好和不良,类的样本个数分别为225和126,每个样本包含34个特征。Robot_Navigation数据集为Scitos G5移动机器人的墙面导航任务,笔者选择2个超声传感器采集机器人3种行为的数据集进行聚类,机器人的3种行为分别是轻微右转、向右急转和向前行进,类的样本个数分别为50、54和52,包含2个样本特征。Wine数据集包含了178个样本,每个样本有13个特征,其中包括了酒的化学成分。该数据集是分类问题,用于区分3种不同来源的意大利葡萄酒。Breast Cancer Wisconsin(Diagnostic)数据集包含了569个样本,每个样本有30个特征,用于诊断乳腺癌。该数据集是一个二分类问题,用于区分良性肿瘤和恶性肿瘤。刀具振动信号数据集涵盖了刀具在3种类型磨损情况下不同的振动信号,包含初期磨损信号150个,中期磨损信号37个,急速磨损信号20个。
2.2 结果分析
首先,对笔者构建的具有不同特点的二维高斯分布的数据集,分别运行K-means、FCM和笔者算法,聚类结果如图2所示。不同灰度的点代表不同的数据类,“+”代表笔者算法确定的聚类中心。

图2 笔者算法聚类结果
通过聚类结果可以看出,K-means算法能对图3a均匀分布的数据集和图3c正确分类。对图3b中20个类的分布不均匀数据集,K-means算法将右下角的2类错分成1类,将右上部分的1个类分成2类,而且对图3d的不平衡数据集分类结果较差。FCM算法能对分布均匀的数据集、重叠数据集和不平衡数据集较好地分类。但对图4b的20个类的分布不均匀数据集,其将右上角的2个类错分成1类,右上部分的1个类分成了2类,未取得正确的聚类结果。笔者算法在多类数据集、重叠数据集和不平衡数据集等不同特征数据集上,均能准确确定聚类个数,并且具有较好的聚类效果。
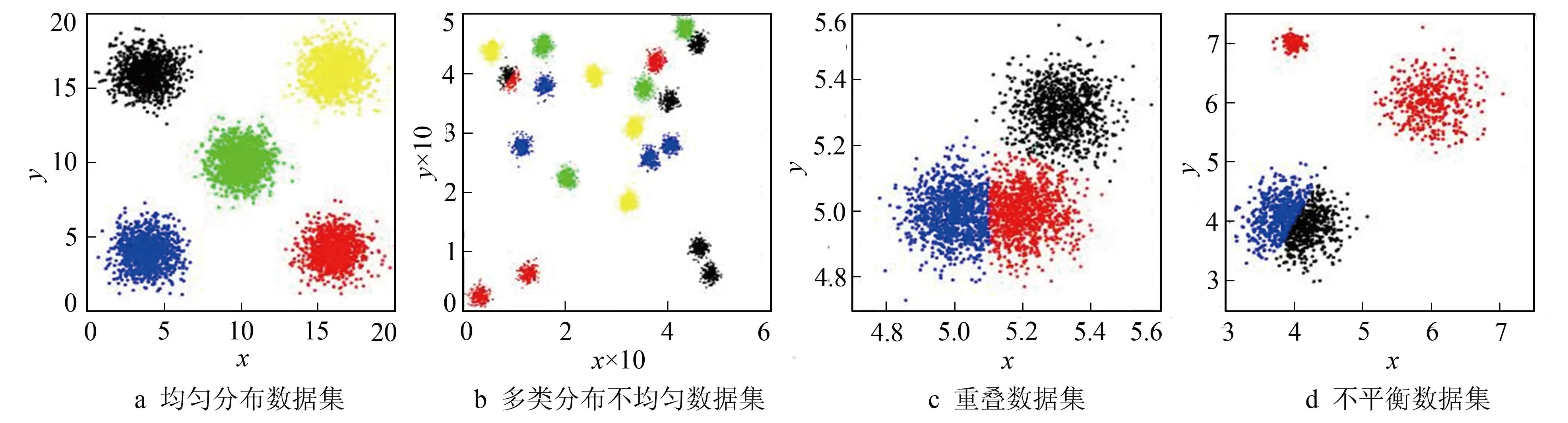
图3 K-means算法聚类结果

图4 FCM算法聚类结果
2.3 全局最优性能实验
使用UCI数据集对本算法进行检验,以此判断其全局最优性。选择的6个数据集为Iris,Statlog(Heart),Ionosphere,Robot_Navigation,Wine和Breast Cancer Wisconsin(Diagnostic)。笔者使用3个评价指标:精确率(Precision,P)、召回率(Recall,R)和调整兰德系数(ARI:Adjusted Rand Index)评估算法的聚类性能。精确率是真正的正样本占预测为正例样本的比例:
(15)
召回率是正例被预测正确的比例:
(16)
ARI的取值范围在[-1,1]之间,ARI结果为正值时,说明聚类效果较好:
(17)
其中NTP为真阳性,NTN为真阴性,NFP为假阳性,NFN为假阴性。
为验证笔者算法的有效性,将笔者算法与传统K-means算法、FCM算法和GKM算法在不同UCI数据集上聚类,评价指标对比结果如表2所示。
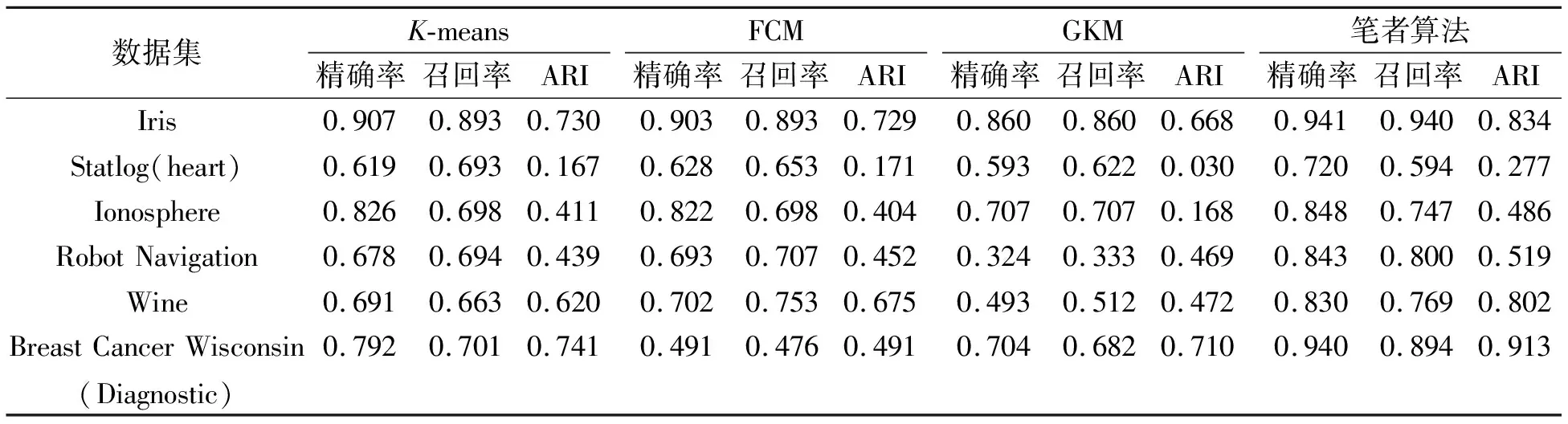
表2 4种算法聚类结果对比
从表2可看出,笔者所提方法在不同的UCI数据集上聚类的各项评价指标效果与K-means算法、FCM算法和GKM算法相比有明显的提升。在实验的对比结果中,除在Statlog(Heart)数据集上的召回率不如其他3种聚类算法外,在Iris数据集、Ionosphere数据集、Robot Navigation数据集、Wine数据集和Breast Cancer Wisconsin(Diagnostic)数据集上聚类结果相较于其他3种聚类算法,在精确率、召回率及ARI评价标准上都具有明显的优势。因此可以证实笔者算法的有效性。由于笔者算法具体聚类过程还是依靠于K-means算法,未来可以结合笔者算法在确定聚类中心和聚类个数上的贡献,在聚类过程中进一步提高算法聚类的准确度。
比较2种算法对刀具振动信号数据集的聚类效果,207个振动信号样本中,K-means算法在该数据集的聚类的结果为:初期磨损信号66个,正常磨损信号125个,急剧磨损信号16个,算法最终识别准确率为75.8%。笔者算法在刀具振动信号样本数据集上聚类结果为:初期磨损信号42个,正常磨损信号158个,急剧磨损信号7个,算法最终识别准确率为84.1%。由聚类结果可看出,笔者算法在实验数据集上得到的聚类准确率更高,可有效用于刀具磨损状态监测分析中。综上,笔者算法通过在不同特征数据集上的聚类取得了理想的聚类效果,能解决K-means算法不能确定初始聚类个数和聚类中心的问题。
3 结 语
由于传统K-means算法在聚类过程中需要事先知道聚类个数,且随机选取初始聚类中心容易使聚类结果陷入局部最优的情况,因此笔者提出一种无参数K-means聚类算法。在高斯数据集、UCI数据集和真实刀具振动信号数据集上分别进行了聚类实验。实验结果表明,与其他同类算法相比,无参数K-means聚类算法既具有传统算法的全局最优性,又在不同类型的数据集上取得了良好的聚类效果。此外,该方法可用于数控机床刀具磨损状态的识别,由于K-means是一种无监督聚类方法,在获得较优刀具状态识别结果的同时,可减少人工数据标定,有监督训练等工作量及运算成本,对准确实时提取数控机床刀具运行状态具有较高的实际意义。由此可见,笔者无参数K-means算法弥补了K-means算法所存在的缺陷,即无法确定初始聚类个数和初始聚类中心随机选取而导致的局部最优问题。然而,笔者算法具体聚类过程仍然依赖于K-means算法,未来可以结合本文算法在确定聚类中心和聚类个数上的贡献,在聚类过程中进一步提高算法聚类的准确度。
