VMD-HS-BP光伏发电功率预测模型的构建研究及试验分析

国网河南省电力公司安阳县供电公司 韩德利

1 引言

在“双碳”政策背景下，电力行业如何实现节能减碳已经成为热点话题，大力推进电力行业可再生能源发展迫在眉睫[1]。在众多可再生能源中，太阳能因具有清洁性、可持续性等优势，使太阳能发电的关注度较高。相比于其他可再生能源发电技术，太阳能发电技术应用较为广泛，发展较为成熟[2]。据国家能源局数据，截止到2022年年底，我国太阳能发电装机容量累计达4亿kW，同比增长28.1%，全年新增容量达8741万kW，同比增长60.3%[3]。然而，光伏并网的数量攀升对电网运行稳定性造成了一定的冲击，光伏电网面临着运行不稳定、运行调度难等问题。为了保障光伏并网的稳定推进，需要构建精准的光伏发电功率预测模型[4]。本文在借鉴相关学者研究基础上，结合了变分模态分解法（VMD）与和声搜索算法（HS），对传统BP 神经网络进行改进，构建了VMD-HS-BP 光伏发电功率预测模型[5]。

2 模型构建

为了进一步提升光伏发电功率预测精准性，本文采用VMD 与HS 算法对BP 神经网络进行改进，构建光伏发电功率预测模型，具体流程如下。

一是相关性分析。采用相关性分析法对输入变量与输出变量之间的相关性进行检验，并从中剔除了相关性水平较低的变量。采用相关性分析法对相关性水平较低的变量进行剔除，可以有效降低冗余变量数量，避免此类变量对结果精准性的影响，并且可以通过相关性分析结果衡量不同影响因素对光伏发电功率的影响水平，具体相关性表达式：

二是VMD 分解。采用VMD 对采集的光伏数据进行分解，并采用中心频率法确定模态数。VMD作为一种全新的多分辨率序列分解技术，在应用中可以将原始序列进行分解处理，序列f（t）可分解为k 个具有相同频率的有线宽带分量，表示为uk（k=1，2，…，K）。此外，该技术在应用中可通过迭代搜寻的方式确定相应的最优解，模型分解后，所有模态分量和具有中心频率的有线宽带在经过初始化后，可对应获取到k 个估算的中心角频率。考虑到变分问题属于约束问题，需通过二次乘法和拉格朗日乘数进行转化分析，在转化完成后，需采用交替方向乘子法进行求解分析，并通过迭代更新方式，获取最终分解模态分量。VMD 的核心思想为构造与求解变分问题，具体操作如下。

初始化各模态、中心频率、拉格朗日乘法算子；更新模态分量uk与中心频率wk，表达式：

更新拉格朗日乘数，表达式：

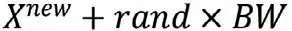
四是光伏序列预测结果输出。使用经过训练的改进BP 神经网络，按照上述流程，依次预测各个分量，并将所有分量的预测值进行叠加，形成最终的预测值，并将被作为本次预测的结果输出。

这个预测过程是基于对光伏序列的深度学习和对大量数据的分析，旨在挖掘隐藏在数据中的规律和趋势，从而提高预测的准确性和可靠性。通过改进的BP 神经网络，可以更好地处理复杂的非线性关系，从而更准确地预测光伏序列的未来走势。在预测过程中，每个分量都经过了严谨的推理和精确的模拟，以确保最终预测值的准确性和可靠性。这些预测值不仅反映了光伏序列的当前状态，还为未来的发展趋势提供了有力的参考。此外，该预测模型还具有思路清晰、逻辑严密的特点。每个步骤都经过了精心设计和严格验证，以确保最终结果的精确性和可重复性。这种严谨的方法不仅提高了预测的准确性，还有助于推动光伏行业的进一步发展。

3 试验分析

3.1 数据处理

以河南电力公司某地区某光伏建筑为模型构建试验对象，光伏建筑总面积约为240m2，建筑顶部布设了光伏发电系统。光伏发电功率预测模型每天在日照时间内采集数据信息，数据采集工作为期一整月，该阶段共计采集获取了1566组数据，采集数据处理中为避免数据误差，进行了归一化处理：

式中，x为样本的各类数据；xmax为样本数据的最大值；xmin为样本数据的最小值。

完成归一化处理后，提出了＜0.5的变量，并进一步计算输入变量与输出变量之间的相关性，其结果见表1。通过相关性分析剔除了小于0.5的输入变量，进而计算输入量和输出量之间的相关性，计算相关系数。

表1 输入与输出变量间相关系数

由上表可知，结合相关系那个分析结果，需要提出＜0.5的变量条件，分别为前一刻试验条件环境温度、前三刻光伏发电功率、风速、相对湿度和大气压。

3.2 变量设置

结合本次试验测试调试要求，选用三层BP 神经网络，其中包含7个输入变量和1个输出变量。其中，BP 神经网络的神经元个数为12个，输入层函使用transig 函数，输出层trainlm 函数，相应算法的具体设置内容见表2。

表2 HS 搜索算法与VMD 算法的具体设置

3.3 试验结果

为进一步验证模型有效性，选择使用BP、HS-BP 和EMD-HS-BP 模型进行对比测试分析，并确定模型的相对误差。运用平均绝对百分比误差和均方根相对误差对几种模型的误差进行评价分析。其中平均绝对百分比误差计算：

均方根相对误差计算：

不同类型模型的预测误差值见表3。

表3 不同类型模型的预测误差值

表3展示了不同类型模型在预测误差方面的表现，其中VMD-HS-BP 模型的预测误差最低，表现出更高的预测精度。相比其他三种同类型算法，本研究所提出的VMD-HS-BP 模型在应用性和准确性方面更胜一筹。具体来看，BP 模型的预测误差较大，MAPE 为15.62%，RMSPE 为0.47%，这表明该模型的预测效果不太理想。而HS-BP 模型在MAPE 和RMSPE 方面均有所降低，分别为7.69%和0.29%，说明该模型在预测精度方面有一定提升。EMD-HS-BP 模型和VMD-HS-BP 模型在预测误差方面表现更为出色。EMD-HS-BP 模型的MAPE 为5.41%，RMSPE 为0.23%，相比HS-BP模型，其在预测精度上有明显提升。而VM DHS-BP 模型的MAPE 和RMSPE 分别为2.04%和0.07%，其预测误差最低，表现出更高的预测精度。综上所述，本研究所提出的VMD-HS-BP 模型在所有对比模型中具有最低的预测误差，显示出更高的预测精度和应用性、准确性方面的优势。这一结果表明，VMD-HS-BP 模型在处理实际问题时具有较高的实用价值。

4 结语

本文提出了一种VMD-HS-BP 光伏发电功率预测模型，该模型能够有效提升光伏发电功率预测精度。以河南电网某地光伏建筑为试验对象，并根据模型运行要求确定了相应的参数设定条件与输入变量信息。在试验验证中，运用相关性分析方法对输入数据变量与输出数据变量进行了分析，剔除了不符合要求的条件变量。为进一步验证VMD-HS-BP 光伏发电功率预测模型的预测精度，在试验中引入了三种同类型模型进行对比测试，通过平均绝对百分比误差和均方根误差结果对比，确定了本文所提出的光伏发电功率预测模型准确性更高，具有较高的实用价值，能够为电网光伏发电功率预测提供参考。