逆向思维在初中数学解题中的应用

张晶晶

摘要：逆向思维是初中学生不可或缺的一项思维能力，是数学核心素养的重要体现.本文中分析了逆向思维在数学解题教学中的重要性，介绍了逆向思维能力在初中數学解题中的应用实例，并提出了学生逆向思维的培养策略.

关键词：逆向思维；初中数学；实践

《义务教育数学课程标准（2022年版）》指出，数学课程要培养学生的核心素养，包括会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界[1].根据思维方向的顺、逆之别，又可把数学思维分为正向思维和逆向思维[2].因此逆向思维是数学思维的重要组成部分，是数学核心素养的重要体现.培养学生的逆向思维，使其能够灵活地分析和解决数学问题是培养学生核心素养的本质要求.

1 逆向思维的含义

逆向思维是相对于顺向思维而言的.在思考数学问题时，按通常思维的方向进行思维称为正向思维，而按照相反方向进行的思维称为逆向思维.逆向思维是一种发散性思维.在解决问题时，采用逆向思维，往往能打破常规的思维模式，更容易找到解题思路.

2 培养学生逆向思维在初中数学教学中的重要性

根据皮亚杰的认知阶段理论，初中学生正处于形式运算阶段，是形成推理能力的关键时期，而推理能力是义务教育阶段数学思维的主要表现之一.作为数学思维重要组成部分的逆向思维，在帮助学生深入理解学科内容、灵活选择数学方法、开拓思维空间方面起着重要作用.

2.1 有助于学生深入理解学科内容

相比于小学阶段对经验感悟的重视，初中阶段更侧重于对抽象概念的理解.如果学生只按常规思维理解概念，往往不够深刻，在解题时会出现思维误区，而逆向思维能够帮助学生从反面理解，不仅知道什么是对的，而且知道什么是错的，从而扫除理解上的盲点，更加全面深入地理解概念的内涵和外延.除了概念理解，逆向思维对于学生学习公式、定理等数学内容都起着重要作用.

2.2 有助于学生灵活选择数学方法

在解决数学问题的过程中，经常有多种不同的方法都能解决同一个问题，但不同的数学方法所对应的解题难度和效率是不同的.逆向思维是一种”反其道而行之”的思维，可以帮助学生从结果入手分析问题或从问题的反面寻求解题方法，往往能简化解题过程，提升学生思维的敏捷性，提高解题效率[3].

2.3 有助于开拓学生的思维空间

培养逆向思维通常有两种方式，一种是把过程反过来思考，另一种是把结果反过来思考.而无论哪种方式都有利于学生打破思维定势，从不同的角度看待问题，从不同的方向思考问题，破除了思维的单一性，拓展了思维空间，是培养学生创新思维的重要途径.

3 逆向思维在初中数学解题中的应用

3.1 利用逆向思维找到解题突破口

初中生的思维能力还处于发展时期，在实际教学中，教师如果难以帮助学生建立解题模型，那么学生也就很难形成相应的解题思路.因此，教师要找准问题的切入点，以更好地引导学生进行逆向思考.初中数学中存在许多几何证明问题，而几何证明是培养学生逆向思维能力的关键.在教学中，教师要抓住材料和载体的作用，引导学生探究，培养学生的创新思维能力.

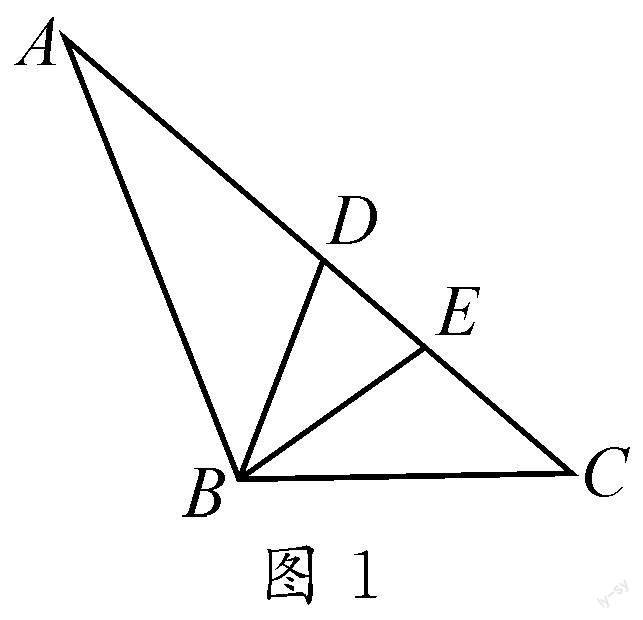
例1 （北师大版九年级上册数学教材“图形的相似”一道课后题）如图1，在△ABC中，D是边AC上的一点，∠CBD的平分线交AC于点E，且AE=AB.求证AE2=AD＼5AC.

本题运用正向思维由条件出发分析问题难以找到证明思路，但从问题出发运用逆向思维却很容易想到将结论看成线段的比例关系，而线段作为三角形的

3.2 利用逆向思维简化解题过程

数学逆向思维具有灵活性的特点[4].在解决问题的过程中，有一些问题利用正向思维从条件入手也可以解决，但过程比较繁琐，学生容易因为计算量大或步骤过多而出错.这时从问题入手，利用逆向思维往往会极大地简化解题过程，提高解题的正确率.

3.3 利用逆向思维巧解证明问题

在数学解题方法中，反证法是体现逆向思维的重要方法.反证法是先假设命题结论不成立，然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果，从而证明命题的结论一定成立.由于反证法需要严密的逻辑推理以及对已知条件、已知定理等的熟练掌握和灵活运用，因此学习运用反证法对初中学生的逻辑思维能力和解决问题的能力都有很大的帮助.

例3 （北师大版八年级上册数学教材“平行线的性质”一节中利用反证法证明定理“两直线平行，同位角相等”）

已知：如图2，直线AB∥CD，∠1和∠2是直线AB和CD被直线EF截出的同位角.求证：∠1=∠2.

证明：假设∠1≠∠2，那么过点M作直线GH，使∠EMH=∠2，如图3所示.根据“同位角相等，两直线平行”，可知GH∥CD.又因为AB∥CD，这样经过点M存在两条直线AB和GH都与CD平行.这与基本事实“过直线外一点有且只有一条直线与这条直线平行”相矛盾.这说明假设不成立，所以∠1=∠2.

由此证明了“两直线平行，同位角相等”.

对于从正面很难说明的问题，比如，“∠2是无理数”“一个三角形中不能有两个角是直角”等应用反证法往往能够严谨地证明.解决这样的问题，可以促进学生逻辑推理能力的发展.

逆向思维可以在一定程度上帮助学生避免解决问题时陷入思维误区而不自知.逆向思维能让学生从单纯的解决问题，转移到对数学思维能力的培养上，从而激发出对数学问题的探究热情，并在解决问题时体会到学习数学的快乐.

4 学生逆向思维的培养策略

（1）夯实基础知识

学生逆向思维的培养要以扎实的基础知识为前提.学生首先要明确什么是正向才能理解什么是反向，如果盲目强调逆向思维会让学生不知所措.而逆向思维对基础概念、公式、定理的理解又起到了促进作用.

（2）树立逆向思维意识

要培养学生的逆向思维，教师应在授课过程中培养学生逆向思考的意识，引导学生在解决问题时从不同

的角度积极思考，不要局限于单一解法.

（3）强化逆向思维专项训练

逆向思维的培养不是一朝一夕就能完成的，它是长期的过程.专项练习可以强化学生的逆向思维，让逆向思维深入学生的脑海，遇到问题可以灵活应用.

逆向思维可以帮助学生明确问题的解决途径，拓展解题思

路，创新解题方法.在初中数学解题教学中注重培养学生的逆向

思维，可以丰富学生的视角，使思维更灵活，提升数学核心素养.

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2022版）[S].北京：北京师范大学出版社，2022.

[2]程晓亮，刘影.数学教学论[M].3版.北京：北京大学出版社，2011.

[3]项赟蒋.逆向思维在初中数学解题教学中的应用分析[J].数理化解题研究，2021（14）：4-5.

[4]傅海伦，张佩雯，徐小惠.对数学逆向思维的再认识[J].教学与管理，2017（19）：45-47.