三维路径规划中改进蚁群算法搜索策略

冯勇超，万广喜，曾 鹏

(1.中国科学院 网络化控制系统重点实验室，辽宁 沈阳 110016；2.中国科学院沈阳自动化研究所 工业控制网络与系统研究室，辽宁 沈阳 110016；3.中国科学院 机器人与智能制造创新研究院， 辽宁 沈阳 110169；4.中国科学院大学 计算机科学与技术学院，北京 100049)

0 引 言

路径规划是控制移动机器人的关键技术之一，深度优先搜索算法、广度优先搜索算法[1，2]、Dijkstra算法[3]、遗传算法[4]、粒子群算法[5]、神经网络法[6]、A*算法[7]等更适合用于二维环境中的路径规划；毛嘉琪[8]、陈志等[9]所提出的蚁群算法均在二维环境中有较好应用。但在实际加工制造环境中，研究蚁群算法三维路径规划问题更具有生产意义。常采用快速搜索随机树算法、人工势场法[10]、蚁群算法[11]等算法研究三维路径规划问题，一般的三维路径规划算法具有计算过程复杂、信息存储量大、难以直接进行全局规划等问题。本文采用将离散点作为信息素载体的方式可较好解决此问题。蚁群算法具有分布式计算的特点，节约计算时间，提升整体计算效率，在路径规划上有很大发挥空间，目前有诸多学者将蚁群算法应用到不同机器人的三维路径规划之中。文献[12]结合人工势场法强化目标路径，修改了蚁群算法的启发值参数，并提出了吸引素概念，有效提高算法收敛速度。文献[13]将机械臂末端限制在矩形区域内，以此来简化搜索空间，提高蚁群算法搜索效率；但这样做限制了算法搜索出更优路径，增强了算法的局限性。文献[14]在传统的复杂山地环境下机器人路径规划中，针对机器人无法攀爬等问题，在启发函数中引入了坡度相关函数，使算法所规划出路径的坡度更好适配机器人爬坡能力；并根据等高线原理改进算法，极大提高算法搜索速度。文献[15]根据三维水下环境的海水流动因素，引入了一阶导数和二阶导数对蚁群算法的信息素更新规则进行改进，并分段修改蚂蚁启发函数，避免收敛速度慢和易于陷入局部最优等问题，以上所介绍算法均有各自的优点，但同时也具备局限性。传统蚁群算法应用于复杂三维空间中仍具有搜索效率低的特点，故提出改进蚁群算法；本文针对三维空间避障路径规划问题的研究主要集中在以下方面：①应用蚁群算法路径规划，改变其规划中选择路径的方式，建立与贪婪算法相结合的概率策略，能有效解决三维路径规划速度慢的问题；②调整适应度函数约束条件，改进信息素计算公式，使其随迭代次数动态更新；减缓信息素前期的积累速度，可避免算法提前陷入早熟。仿真实验结果表明，改进蚁群算法可较快规划出合理的路径，可有效解决复杂山地环境下机器人路径规划问题。

1 地图建模

这部分通过数学模型的方式将本文所研究物体的运动空间进行合理表达。本文空间地图采用栅格法建立，栅格的大小决定构建地图环境的精细程度，栅格越小，地图所存储的信息越多，但会降低规划精度；栅格越大，地图存储的信息越少，路径规划速度会相应增快，但不利于规划出有效的路径规划。合理选择栅格大小有利于规划出最优路径。本文栅格大小采用1 km*1 km*0.2 km。

1.1 三维空间建模

三维空间模型的具体建模方法如下：将三维空间中左下方顶点与三维地图的坐标原点O重合，并在点O处建立三维坐标系，沿坐标轴方向构建三维空间立方体区域ABCO-EFGH，该立方体区域是物体的运动空间，即为本次规划的空间。采用等分法对空间进行划分，首先沿着OC使用A1O1H1E1，A2O2H2E2，……，An-1On-1Hn-1En-1等n-1个平面将空间划分为n个等分区域，同理沿着OA将空间等分为n个等分区域，最后沿着OZ将空间等分为m个等分区域。最终整个空间被划分成具有n×n×m个栅格。蚂蚁可移动的区域为每个栅格上的8个顶点，三维路径规划空间如图1所示。

图1 三维空间规划网格

1.2 初始地图建模

本文随机生成的三维地图如图2所示，图中下方点为路径搜索的起点，上方点为路径搜索终点。产生的地图可作为复杂山地环境的建模应用，形状起伏的表面模拟作为障碍物的山峰，x轴方向作为经度方向，y轴方向作为维度方向，Z轴方向作为海拔高度方向。

如图3所示，设置蚂蚁每次寻找路径沿x轴向终点方向移动一个单位长度，沿着y和z的正负轴方向最大可移动两个单位长度，蚂蚁在p点选择下一节点时共有25种可选择的移动方向。

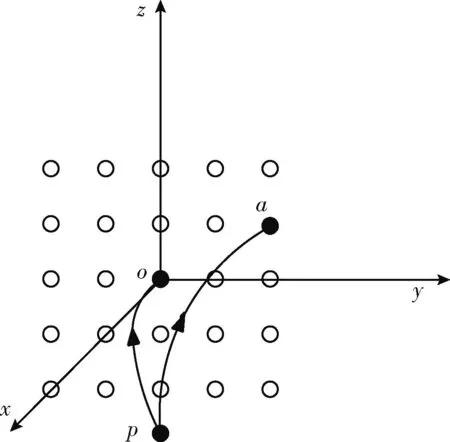
图3 下一节点选择

定义1 可行节点定义：对平面AnOnHnEn上任一点pn(in，jn，kn)， 若线段pn-1pn不与地图内任何障碍物相交，则将pn存入集合allowed(i，j，k) 中，计算当前点pn可通过的所有可行节点并将其存入到集合allowed中作为待选点。

2 基本蚁群算法

蚂蚁寻找食物过程中，会释放一种名为信息素的生物信号，蚁群行进过程中，能够识别信息素强弱程度，并根据识别出的结果来指引下一步的移动方向。相同时间内，距离短的路径上信息素浓度会更高，蚂蚁会逐渐向这条距离短的路径聚集，同时信息素强度会随时间进行挥发。

蚁群算法的数学模型可描述如下：规划空间中的所有节点由集合C={C1，C2…Cn} 表示，连接空间中n个节点间的直线路径由集合P={Pij|i，j=1，2，…，n；pi，pj∈C} 表示，路径的长度用集合Dij{i，j=1，2，…，n} 来表示。在t时刻每条路径上的信息素用集合T={τij(t)|i，j=1，2…n；i，j∈C} 来表示，每条路径在初始时刻都具有一定量的信息素浓度，且信息素浓度大小相同，本文规定初始信息素浓度τij(0)=1。 通过转移概率、局部信息素更新和全局信息素更新规则构成蚁群算法主体框架，并实现算法的寻优过程。

在算法的搜索过程中，所有蚂蚁组成的集合用K={1，2，……，m} 表示，蚂蚁经过的节点用集合ban={1，2……，n} 表示。蚂蚁s(s∈K) 向下一点移动时，是根据所有可选点的概率进行选择的，从当前点i选择下一点j的概率可以表示为

(1)

式中：j∈{allowed}，k∈{K}，α为信息素启发因子，反应信息素对选择概率的作用程度；β为期望值启发因子，决定环境影响选择概率程度的大小；ηij为启发函数，计算公式如式(2)所示

ηij(t)=1/dij

(2)

完成一次迭代过程后，此时所有蚂蚁均完成从初始点到终点的路径搜索，全局信息素在此时进行更新，更新规则如下所示

τij(t+Δt)=ρ1τij(t)+Δτij(t+Δt)

(3)

(4)

(5)

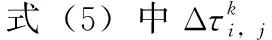
3 蚁群算法设计与改进

3.1 改进算法转移概率规则

传统蚁群算法采用轮盘赌方式选择下一步路径，这样算法选择的随机性强但效率低下；贪婪算法是指在问题求解时中，选取局部最优，不从整体上考虑最优。改进贪婪蚁群算法的机制是每一次路径，下一个节点选择前按照传统蚁群算法概率选择式(1)，计算出所有可选点概率并取出概率最大点的值Pmax，后取随机值rand∈(0，1)， 若rand≤Pmax， 下一点概率公式选择式(6)，否则采取普通蚁群算法概率式(1)。按照此种方法算法能够快速收敛，极大地提高算法的求解效率，且不失算法搜索随机性

(6)

式中：τis为所有待选点的信息素浓度，ηis为启发函数，α，β分别为适应度启发因子和期望值启发因子，{alloweds}=C-{ban}。

3.2 信息素更新规则改进与表示方法

信息素载体通常选择相邻两节点间的路径，但三维空间较为复杂，设每一个平面AnOnHnEn中有n2个节点，则相邻两个平面AnOnHnEn与An+1On+1Hn+1En+1的所有节点的连接路径将会有n4种情况，且随着划分间隔距离的减小，n会逐渐增大，连线的情况也会随之变多，故采用路径作为载体，算法计算量过大，空间复杂度过高，计算速度十分缓慢，故信息素不适用于该方式进行表达。

本文采用离散点作为信息素的载体，这样相邻两平面只有n2+n2个信息素载体量，若将整个地图环境划分为n×n×m大小的栅格，则只需n2×m个信息素载体，极大降低计算复杂度。

路径对蚁群的吸引程度由信息素大小决定，蚂蚁每前进一段距离，路径上的信息素就需要进行一次局部更新。正是这样的实时更新策略，使蚂蚁可以快速的向信息素浓度高的路劲收敛，但若当前路径非最优路径，则会导致算法陷入局部最优。为了避免这种情况，本文新增信息素波动系数值，即随迭代次数动态调节局部信息素值。局部信息素更新公式如下所示

τij(t+Δt)=ζτij(t)

(7)

(8)

其中，ζ∈[0，1] 为局部信息素波动系数值，Δt为算法运行时间，μ和σ为控制参数。

图4显示了局部信息素波动系数随迭代次数变化的曲线，最大挥发系数设置为max=0.81。搜索初期波动系数小是为了让蚂蚁在初期获得更多方向的搜索路径，有利于找出全局最优路径，避免算法陷入早熟；后期波动系数随迭代次数加大，可在搜寻出全局最优路径后，加快算法的收敛速度。

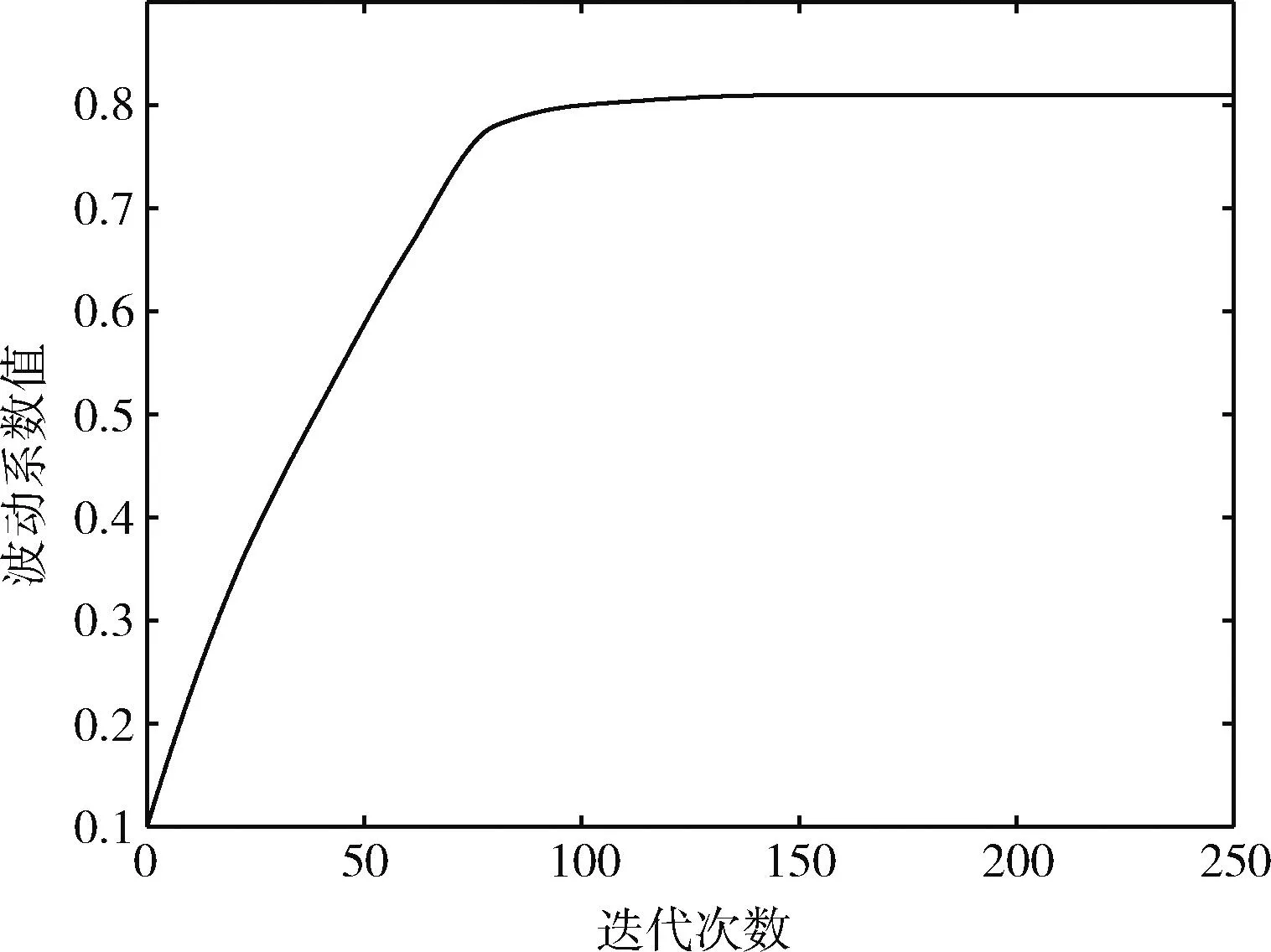
图4 波动系数变化曲线图

在进行一次完整的迭代之后，所有蚂蚁均完成从初始点到终点的路径搜索，全局信息素在此时进行更新，全局信息素的更新规则如式(9)所示

τij(N+1)=(1-ρ)τij(N)+ρΔτij(N)

(9)

(10)

3.3 改进启发值判定规则

采用启发值作为蚁群算法在三维路径规划中，下一节点能否被选择的判定条件，传统蚁群算法的启发值与蚂蚁选择下一局部路径的长度成反比，进而驱动蚂蚁选择短距离路径，但所选路径不一定是最优路径。文献[16]采用障碍物约束条件、当前节点距下一可行节点距离和可行节点距目标节点的距离等3个因素作为启发值评价函数，障碍物约束条件如式(11)所示

(11)

欧式距离作为最短路径，启发函数为式(12)所示

(12)

当前节点的下一可行节点距离目标点距离的启发函数如式(13)所示

(13)

但下一节点距离目标点距离短并不能保证算法所选路径一定是最短的，鉴于此，本文把局部路径长度作为重要指标，采用当前节点距离下一节点的欧氏距离作为衡量启发值函数的指标，启发函数如式(14)所示

ηij(t)=f1·f2

(14)

3.4 适应度值计算公式

蚁群算法采用适应度值的大小作为算法性能评估的指标，适应度值是由当前点与被选择点两点间距离与被选择路径点的高度值组成的[17]，其中 (Yi-1，Zi-1)，(Yi，Zi)， 是路径上选择点与被选点的Y，Z坐标值，Y∈[1，J]，Z∈[1，J]。 适应度值公式如式(15)所示

(15)

4 算法流程

本文算法执行的流程如图5所示：

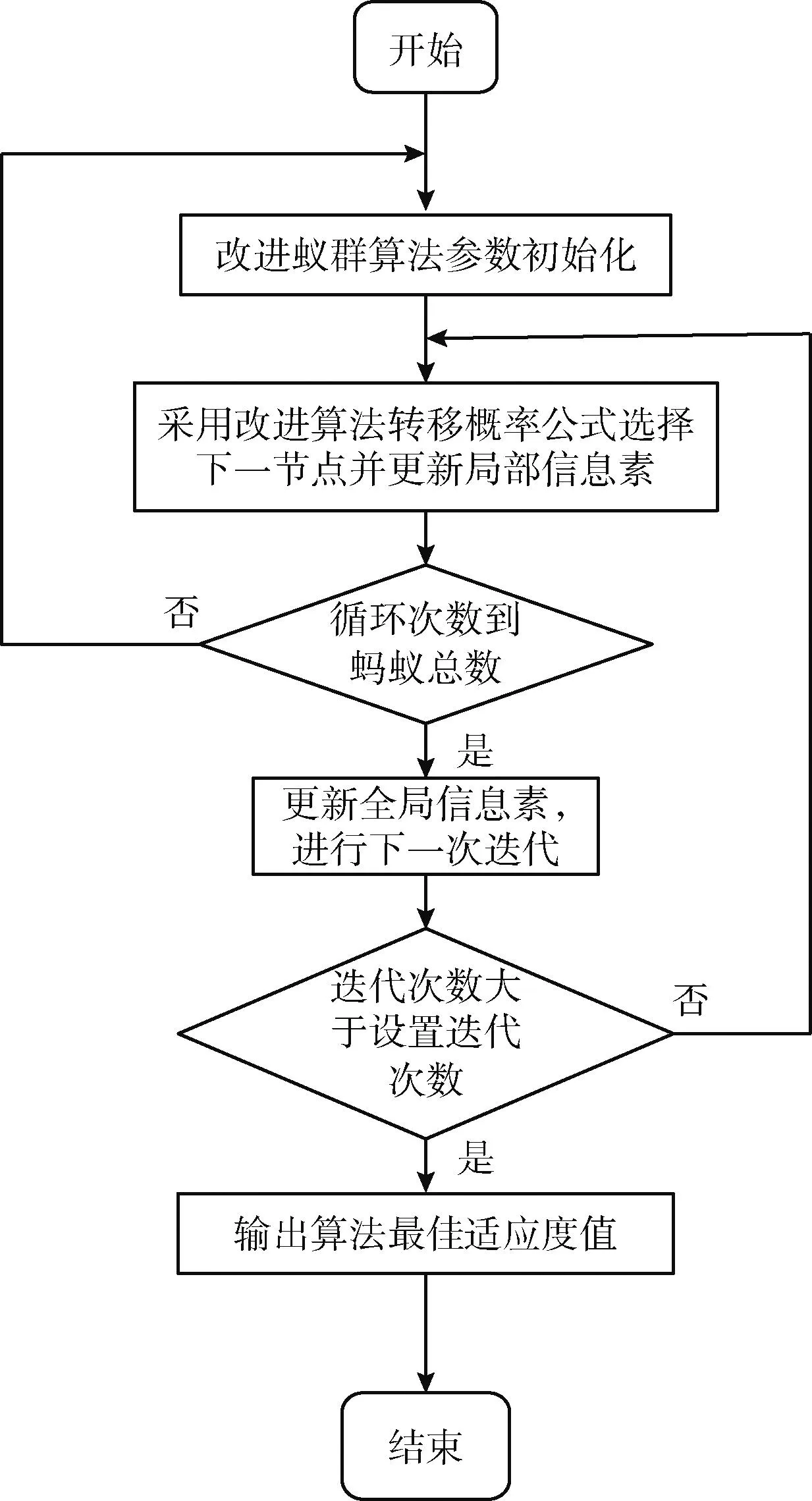
图5 改进蚁群算法流程

步骤1 初始化参数：初始信息素浓度τ(0)=1， 全局信息素强度Q2=100，蚂蚁数量Nmax=10，迭代次数N=200，其中初始位置与目标位置由实验网格环境决定，适应度启发因子α，期望值启发因子β，全局信息素的衰减系数ρ，作为变量根据实验现象分别进行设置。

步骤2 将Nmax只蚂蚁随机放置在起点处。

步骤3 根据改进蚁群算法的转移概率公式，选择下一节点并更新局部信息素，搜索到终点后，一只蚂蚁的完整路径搜索结束。

步骤4 判断循环次数是否小于等于蚂蚁数量Nmax，若满足条件重复步骤3，否则停止循环，一次迭代完成，选出Nmax条路径中的最佳适应度值，对该路径进行全局信息素更新。

步骤5 判断迭代次数是否小于等于N，若小于跳回到步骤2，否则循环结束，找出N次循环中最优的适应度值作为程序最终运行结果。

5 仿真结果

为验证贪婪改进蚁群算法的有效性，选择软件MATLAB2020a作为仿真环境，CPU型号为Intel i5-10400，内存16 GB的计算机。蚁群算法中，算法的参数极大影响着算法的性能，其中主要起作用的参数分别为：信息素启发因子α，期望值启发因子β，全局信息素挥发系数ρ。为了得出最佳参数配置本文采用图2(a)初始地图1的环境进行实验，采用修改一个参数值，其它参数不变的原则。初始默认参数为：蚂蚁数量Nmax=10，迭代次数N=200，信息素启发因子α=1，期望值启发因子β=1，全局信息素挥发系数ρ=0.8，实验结果如图6所示。

图6 α，β，ρ不同取值对算法性能的影响

结果表明在第一次迭代后改进蚁群算法的适应度值远优于文献[12]算法，改进算法最终迭代的适应度值平均值也是较低的，且算法性能随着α，β，ρ等参数的波动变化较小。以上实验结果可以得出，3个关键参数的最优配置为：α=1.5，β=2.5，ρ=0.7。

为验证本文算法的有效性，将其与文献[12]的算法在不同环境下进行对比，首先设置所有参数环境均相同的第一组对比实验。首先选择图2(a)初始地图1，规划路径起点坐标为(1，15，1000)，终点坐标为(21，4，1600)，起点和终点相同的情况下，对比结果如图7所示，其中圆形线为改进蚁群算法，星形线为文献[12]算法。算法的收敛曲线如图7(c)所示，虚线代表文献[12]算法最佳个体适应度收敛曲线，实线代表改进蚁群算法最佳个体适应度收敛曲线。

图7 两种算法路径规划结果对比

第一组实验对比见表1，结果表明改进蚁群算法最终适应度值收敛到110.4840，文献[12]算法最终适应度值收敛到118.0732，适应度值缩小7.5892；改进蚁群算法比文献[12]算法规划出的路径更加简洁，路径转弯次数较少，整体较为平滑。由适应度迭代曲线可以看出，在算法的初期改进算法的迭代速度要优于文献[12]的算法，这是因为改进算法加大了所有待选点中概率最大点被选择的概率，即信息素与启发值大的这些点更易被选择，同时减少了算法向较差路径方向搜索的概率，可以更快搜寻出最优路径。而在经历多次迭代，适应度值不变后，在150次迭代处，本文改进算法仍在进行优化，即说明改进算法具备跳出局部最优解的能力，实验结果表明改进算法拥有极快收敛速度的同时不失搜索随机性。

表1 第一组实验对比

我们在同一地图不同起点与终点设置第二组对比实验。规划路径起点坐标为(1，17，800)，终点坐标为(21，18，1200)时，对比结果如图8所示。

图8 不同起止点两种算法路径规划结果对比

第二组实验对比见表2，结果表明改进蚁群算法最终适应度值收敛到118.0698，文献[12]算法最终适应度值收敛到124.9016，适应度值缩小6.8318；由俯视图可以观察到，本文改进算法规划出路径更加简洁。改进算法前期，由于波动系数较低，故算法会向多个方向搜索，有助于快速的找寻到最优路径，此时最优适应度值处于急速降低状态；随着迭代次数增加，波动系数值增大幅度减缓并趋于稳定，此时算法迅速向最优路径递进，最优适应度值更新趋于平稳。另外采用本文的启发值判定法则，削弱了距终点近的，非最优路径上的点对算法寻优的影响。第二组对比实验验证了本文算法在同一地图不同起点的情况中，同样拥有较好的性能，改进蚁群算法只需很短的时间与迭代次数即可达到文献[12]算法迭代200次所产生的适应度值。但文献[12]算法的迭代200次所消耗时间比本文算法少，本文算法牺牲少部分时间获得更快地收敛速度与更优的适应度值。

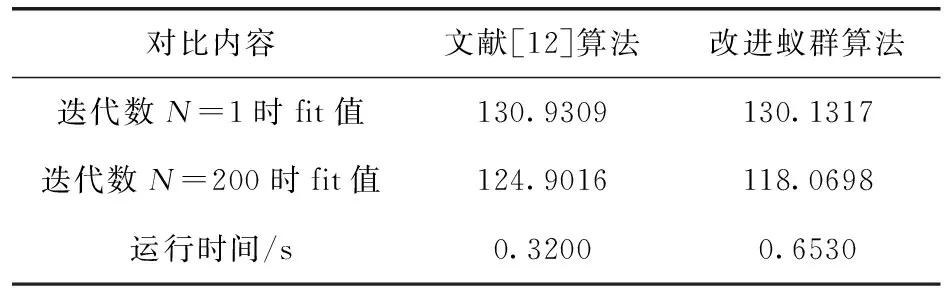
表2 第二组实验对比

当采用图2(b)的初始地形，起点与终点改变，起点坐标为(1，11，1400)，终点坐标为(21，5，1000)参数不变的第三组实验，两算法对比结果如图9所示。

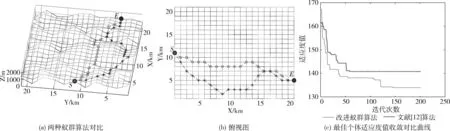
图9 场景二两种算法路径规划结果对比

第三组实验对比见表3，结果表明改进蚁群算法最终适应度值收敛到133.9033，文献[12]算法最终适应度值收敛到140.7637，适应度值缩小6.8604；路径图可以看出改进算法在y方向上是逐渐向终点靠扰，而文献[12]算法在y方向上有越过终点的选择，且只需较小的迭代次数(50次以下)，与运行时间，改进算法就可规划出与文献[12]算法迭代完成所产生的适应度值；实验三验证了改进算法在不同环境中仍然具有较好的性能。

为了验证算法的适应性，设置与图9中起点相同，算法参数相同，初始地形相同的10组对比实验，结果见表4。

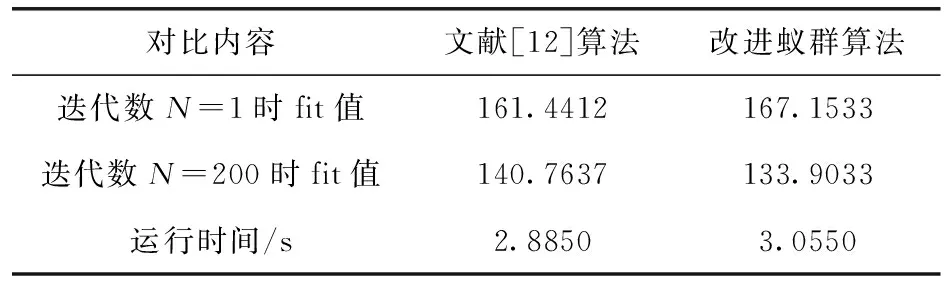
表3 第三组实验对比

表4 10组对比实验

相同地图10组对比实验见表4，第一列为实验序号；第二列和第三列是迭代次数为200时，两种算法规划出的适应度值；第四列和第五列为两种算法达到200次迭代时所运行的时间。实验仿真结果表明，文献[12]算法优化能力较差，需要更多的时间才可以迭代出较好的适应度值；本文所提出的改进蚁群算法在三维路径规划中具有更快的收敛速度、较优的适应度值和更好的稳定性。

6 结束语

移动机器人执行任务过程中，在复杂环境下进行合理的三维避障路径规划能够有效的提升机器人的工作效率与安全性。本文针对蚁群算法在三维路径规划中的缺点，如过多的迭代次数，规划出的适应度值较大、路径过曲折等问题提出了改进贪婪蚁群算法。使用栅格法构建初始地形，通过实验确定算法参数最优组合，通过模拟不同起点终点与地图环境与传统的蚁群算法进行比较。仿真结果表明改进算法具有更快的收敛速度与更优的适应度值。合理解决了复杂山地环境下机器人路径规划问题。本文所研究障碍物局限于静态环境，地图参数已知的情况，这为下一步动态障碍物避障算法的研究打下基础。