气体旋进旋涡流量计信号处理实验研究

徐昊学,毛谦敏

(中国计量大学计量测试工程学院,浙江杭州 310018)

0 引言

旋进旋涡流量计属于流体振动流量计,该流量计利用旋涡进动频率与流速成正比的原理测量流量。它具备测量精确度高、安装维护方便和适应多种介质等优点[1]。由于该类型流量计通过检测流体振动获得流量值,因此,旋进旋涡流量计存在一个固有缺陷,即抗干扰能力差[2]。当被测流体存在脉动干扰或管道受到瞬态冲击振动时,测量系统的误差增大,造成计量误差,最终影响流量计的正常计数,这严重制约了旋进旋涡流量计的进一步发展。

针对上述问题,彭杰纲等提出采用Hilbert-Huang变换(HHT)的方法研究流体脉动对旋进旋涡流量计的影响,得到振荡流中旋进旋涡流量计的响应特性是均匀流中旋进旋涡流量计响应特性和振荡流干扰特性的叠加这一结论,并利用HHT消除流体脉动干扰对流量计测量的影响[3]。马才伟等提出在同侧沿轴向安装2个传感器,其中一个传感器采集流量和振动的混合信号,另一个仅采集振动信号,两者进行差分处理,消除外界振动对流量计的影响,但该方法无法消除流体脉动干扰对旋进旋涡流量计测量的影响[4]。德国菲时波特公司(Fischer&Porter)通过改进检测元件结构增强旋进旋涡流量计的抗干扰能力。使用的压电传感器中2片压电晶体用于检测旋涡振动的频率,另外2片用于检测机械振动信号。4片压电晶体并联进行工作,通过对振动信号进行差分处理,保留旋涡振动信号并转换为流量值[5]。

综上所述,现有研究成果多为单一因素对旋进旋涡流量计测量的影响,没有对干扰因素综合分析;采用改进传感器的方法研发成本高、周期长,在中小企业中推广难度大。因此,本文提出了基于频谱分析的方法提取旋涡频率,分析不同流量区间的旋涡信号与振动响应信号,在外部存在干扰的条件下,可以实现流量的准确测量并通过实验证明了方案的有效性。

1 旋进旋涡流量计工作原理

旋进旋涡流量计的工作原理如图1所示[6]。流体进入旋进旋涡流量计后,首先经过一组由固定螺旋叶片组成的旋涡发生体,使流体强制旋转,形成旋涡流。旋涡流经收缩段加速,再经扩大段急剧减速,由于压力上升,产生回流,在回流的作用下旋涡的涡核围绕流量计轴线作旋进运动[7]。旋涡的进动频率与流量成正比。假设旋涡进动频率为f,则瞬时体积流量Qv符合如下规律:Qv=f/Kv,其中,Kv为旋进旋涡流量计仪表系数。因此,旋进旋涡流量计测量的关键在于准确得到旋涡进动的频率。

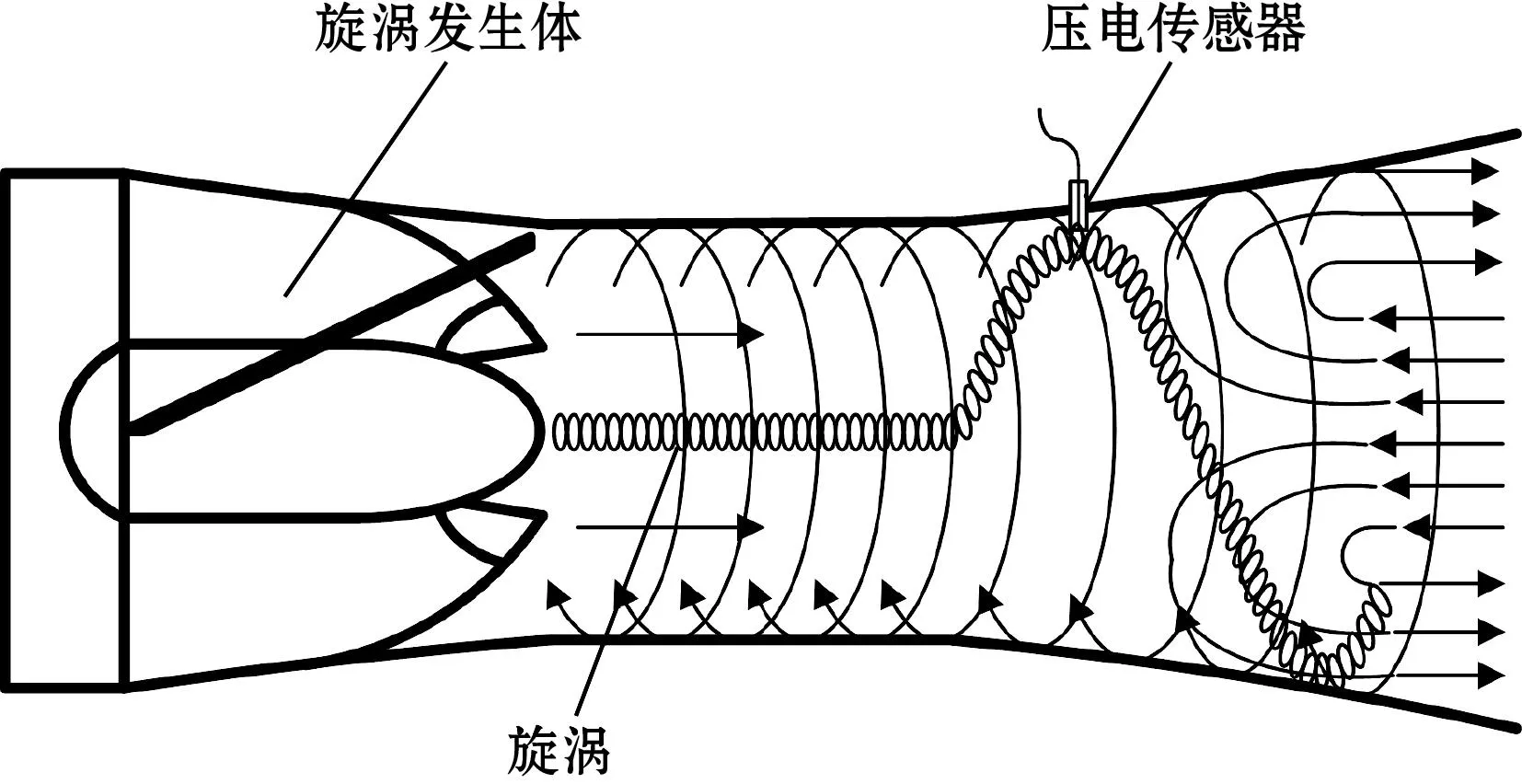
图1 旋进旋涡流量计工作原理图

2 信号处理方法研究

旋进旋涡流量计的检测元件采集信号经电路处理的输出信号中主要包含旋涡信号和干扰信号,分析并比较两种信号的区别,找到差异性最大的特征,即可提取旋涡频率,实现流量的有效测量。

旋进旋涡流量计检测元件采集的旋涡信号可以近似看作正弦信号,在外界无干扰情况下,流量计输出的电压信号为

V0(t)=A0sin(2πf0t+φ0)

(1)

式中:V0(t)为输出信号转换得到的电压值,V;A0为正弦信号的幅值,V;f0为旋涡进动频率,Hz;φ0为信号的相位。

根据三角函数傅里叶变换结果可知[8],在上述信号的单边频谱中,当f=f0时对应幅值最大,因此,可以通过搜索最值的方法反向确定旋涡信号的频率。

在旋进旋涡流量计的实际应用环境中,常见的干扰信号主要为瞬态冲击振动和流体脉冲干扰。根据文献[9]实验研究得到,流体脉动干扰信号在沿流量计轴向对称的方向上非常接近,旋涡产生压力信号在对称位置上反相,因此可以通过差分处理的方式基本消除流体脉冲对旋进旋涡流量计的影响。针对瞬态冲击振动信号,在理想状态下可以看作阻尼振动信号,通过检测元件采集的电压信号可通过式(2)表达[10-11]:

V1(t)=A1e-ηωntcos(ωdt+φn)

(2)

式中:A1为信号的幅值,V;η为阻尼系数;ωn为固有角频率;ωd为振动角频率;φn为初始相位。

从式(2)可以看出,在振动过程中频率始终保持不变,幅值不断减小至0,因此,在对应的频谱图中,当f=ωd/(2π)时对应的幅值最大。实际环境中,振动信号的频谱中可能存在高频谐波。

综合以上分析可以看出,由于旋涡信号始终稳定,对应的能量随时间不断累积,而振动信号初始能量大,随时间变化累积量不断减少,在两者初始幅值基本相同的情况下,旋涡信号的能量必大于振动信号,因此,可以通过频谱分析结果中的幅值最大值来确定旋涡信号的频率,并转化为瞬时流量完成测量。

3 信号采集电路设计

为了验证上述信号处理方案的可行性,需要采集旋进旋涡流量计的输出信号并进行分析,结合以上提出的信号处理方法,本文设计的信号采集方案如图2所示,沿流量计轴向对称分别安装压电传感器F1和F2,经电荷放大电路将电荷信号转化为电压信号,通过差分电路处理得到旋涡进动的电压信号,采用截止频率为1 kHz的低通滤波电路去除其中的噪声,最终输出实验所要采集的信号。

图2 信号采集方案结构框图

电荷放大电路具体原理图如图3所示,通过反馈电容C11、C12的积分作用将电荷量转换成电压量。电容C13、C14的作用为去除输入的直流分量,由于运算放大器为单电源供电,在运算放大器的同向端输入正向的参考电压VREF,大小为电源电压的1/2,抬高采集的电压使其位于运算放大器的工作电压范围内。反向端接入电阻R5、R6的主要作用是防止反馈电容长时间充电导致运算放大器饱和。二级管D1、D2、D3、D4的作用是防止传感器过载产生较大的输出,保护电路。V1、V2为输出的电压信号,经过后续的运算放大器差分后进入低通滤波电路。

图3 电荷放大电路原理图

4 实验研究与结果分析

4.1 实验平台搭建

旋进旋涡流量计实验平台示意图如图4所示,主要由标准装置、管道、PCIe-6320数据采集卡、流量计信号采集电路和DN50气体旋进旋涡流量计实验样机组成。

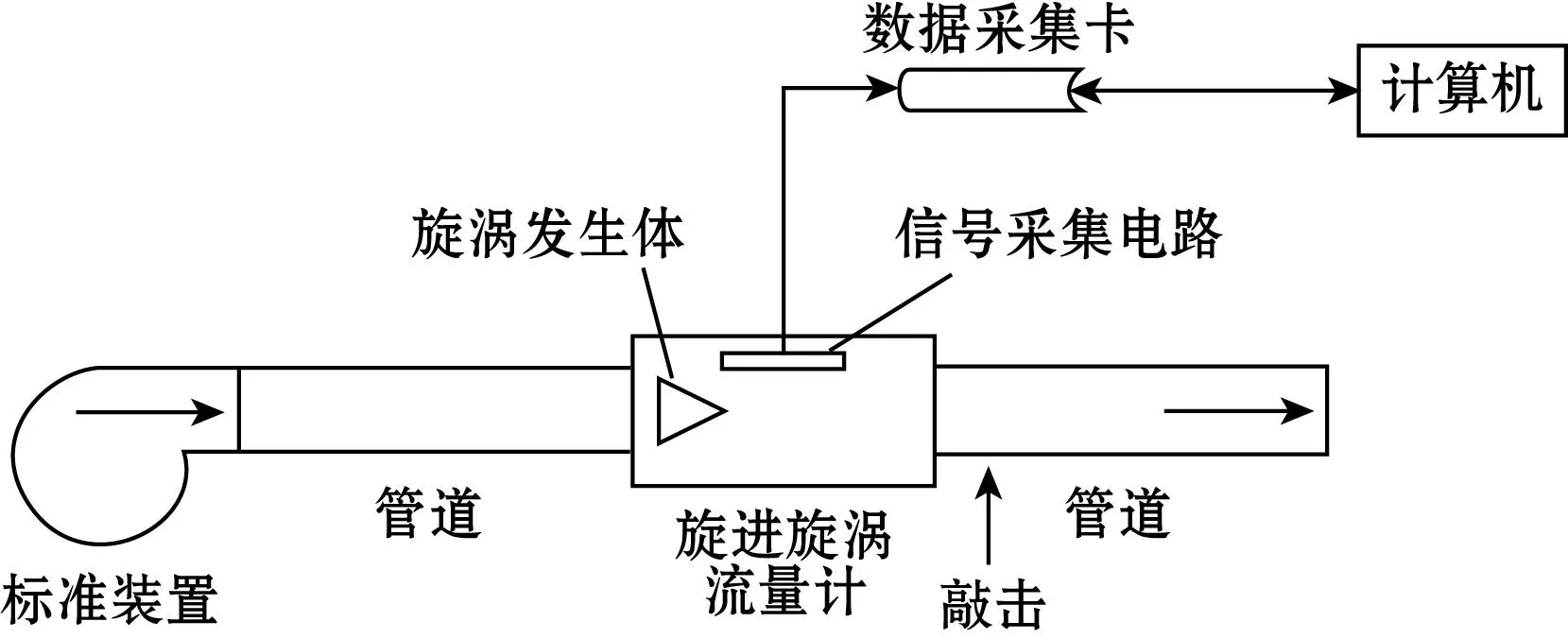
(a)平台结构图

(b)平台实物图图4 旋进旋涡流量计实验平台示意图

实验所用的标准装置精度为0.25级,实验样机的量程为8～120 m3/h,精度为1.5级,则旋涡进动频率大致范围为45～750 Hz。信号采集由计算机上的LabVIEW软件控制数据采集卡完成,根据奈奎斯特采样定理,设置信号采样频率为4 kHz,保证采样的信号不失真。另外,为了减小数据处理过程中的误差,提高频率分辨率,设置采样时间为5 s,使用20 000个数据点进行分析计算。

4.2 信号处理结果分析

由于旋进旋涡流量计在不同流量下对瞬态冲击振动的响应不同,同时,在旋进旋涡流量计行业标准中通过引入分界流量qt对不同范围内的精度与重复性做了相关规定,因此,本文分别对高流量区和低流量区的振动信号响应进行分析,分界流量为量程最大值的1/5,因此,取分界流量qt为24 m3/h。

4.2.1 高流量区信号处理

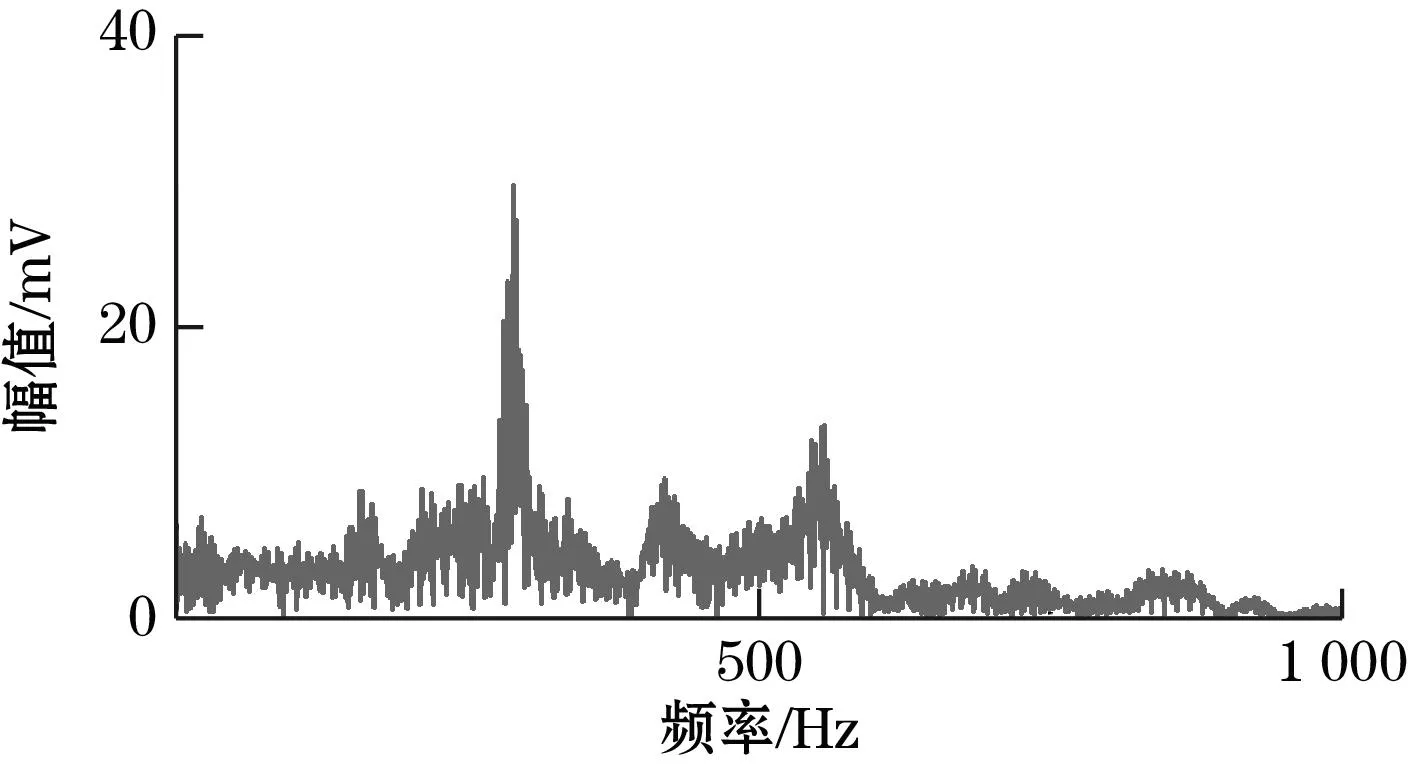
高流量区以流量点41.7 m3/h的瞬时流量信号为例。在流量稳定的情况下完成采集并去除信号中的直流分量并进行处理,由于对信号已进行低通滤波处理,频谱分析得到的结果中1 kHz以上的信号对应幅值基本为0,在图中不做展示,得到的无振动情况下的旋涡信号的时域与频域结果图如图5所示。从结果图中均可以看出,旋涡信号近似于正弦信号,与理论分析相符,信号频率即为频谱图中尖峰对应的频率,通过FFT计算得到结果为258.1 Hz。

(a)信号时域图和局部放大图

对实验平台的管道施加3～4 Hz的敲击振动,得到的时域与频域结果如图6所示。从结果可以看出,振动信号的初始峰值与旋涡信号的幅值基本一致,同时两者的频谱图基本相同,计算得到的信号频率值为257.1 Hz,与稳定状态下的测量结果基本一致。因此,在高流量区由于旋涡信号本身的能量较大,叠加的振动信号不会影响旋涡频率的测量结果,可以直接通过FFT分析获得旋涡频率。

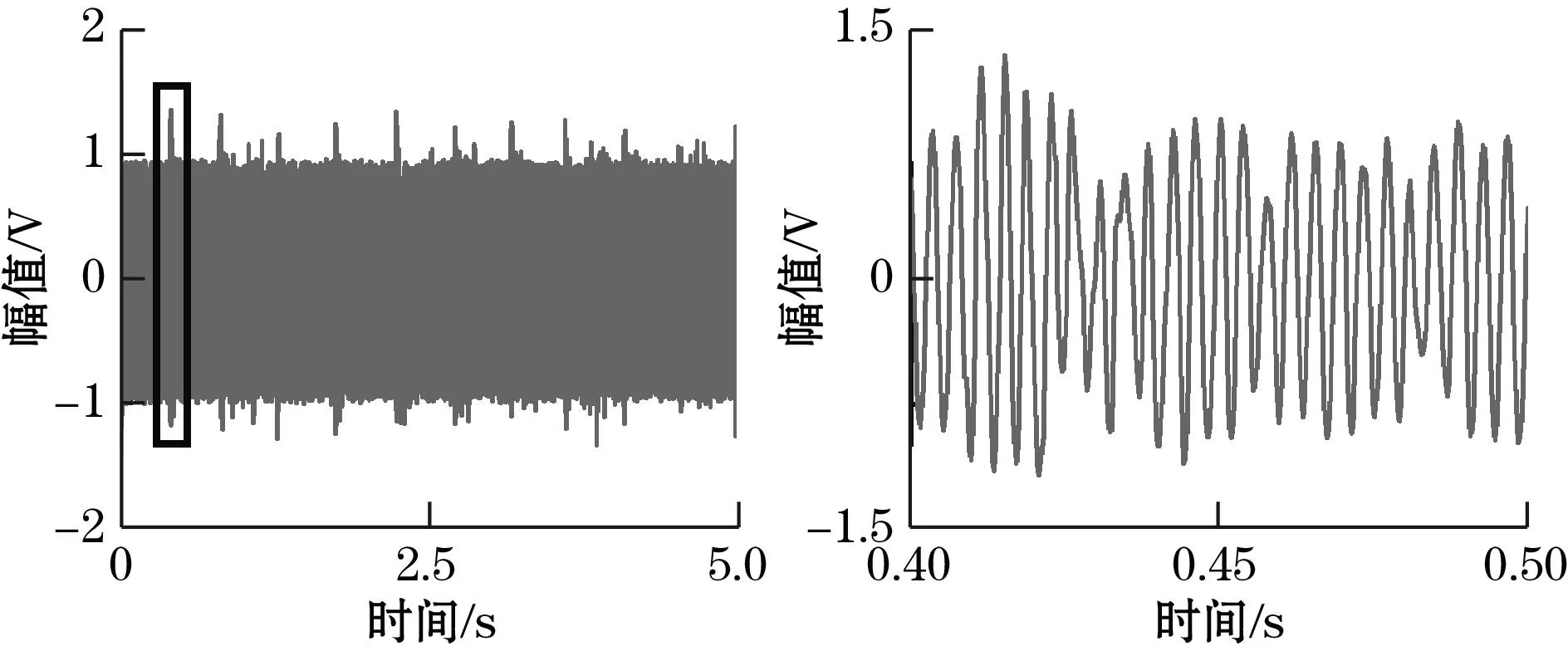
(a)信号时域图和局部放大图

(b)信号频谱图图6 高流量区振动响应时域和频域结果图

4.2.2 低流量区信号处理

低流量区以流量点9.0 m3/h的瞬时流量信号为例,采集得到的无振动情况下的旋涡信号的时域与频谱图如图7所示,200 Hz以上的信号分量基本为0,未在结果图中展示。从结果可以看出,虽然存在一部分高频噪声,旋涡信号的幅值有跳动的情况,但仍然不会影响流量计的测量结果,同高流量区采用相同的方法计算信号频率为54.0 Hz。

(a)信号时域图

(b)信号频谱图图7 低流量区旋涡信号时域和频域结果图

同样对实验平台的管道施加3～4 Hz的敲击振动,得到的时域与频域结果如图8所示,为了便于后续的分析与比较,时域图显示其中1 s内的波形。从结果可看出,由于振动信号的初始峰值与旋涡信号的幅值不在同一量级,FFT分析得到振动信号对应的尖峰高于旋涡信号,因此,无法直接得到旋涡信号的频率,对于这种非平稳信号,可以通过经验模态分解(EMD)提取振动信号对应的本征模态函数(IMF),差分处理后再进行FFT变换获得旋涡信号频率。

(a)信号时域图和局部放大图

(b)信号频谱图图8 低流量区振动响应时域和频域结果图

定义为IMF的条件有以下2个:

(1)整个信号中,极值点数量必须与过零点数量相等或差值为1;

(2)在任意时刻,信号极大值与极小值包络的均值为零。

原始信号x(t)分解过程为:首先提取信号的极大值与极小值,通过三次样条插值得到包络信号计算其平均值mi(t),判断差值hi(t)=x(t)-mi(t)是否为IMF分量,如果不是,则将差值作为下一次分解目标并重复以上步骤,直到得到本征模态函数IMFk(t)。每次提取IMF后,从原始信号中减去对应的本征模态函数,再进行下一次分解,直到最后的信号中不存在IMF,最终,原始信号可以表示为[12]

(3)

式中:n为IMF的个数;ε(t)为信号的残差。

上述信号进行分解后得到的一阶本征模态函数时域与频域结果如图9所示。从结果可以看出,EMD处理后得到的本征模态函数基本保留了原有振动信号的所有特征,幅值较大处对应的频率基本一致。

(b)信号频谱图图9 一阶模态函数时域和频域结果图

将两种信号差分处理,对应的信号时域与频域结果如图10所示。从结果可以看出,振动信号的能量得到有效去除,频谱图基本不存在高频振动信号,计算频谱图中尖峰峰值对应的频率为54.0 Hz,与稳定条件下的旋涡信号频率一致,证明本方案在实际应用中具有可行性。

(a)信号时域图

(b)信号频谱图图10 差分信号时域和频域结果图

4.3 流量计性能测试

按照JJG 1121—2015《旋进旋涡流量计》的检定要求,对流量计进行标定,得到瞬时流量Q(m3/h)与频率f(Hz)之间的函数关系式如下:

(4)

对实验平台管道施加3～4 Hz的振动信号,在旋进旋涡流量计的量程内,任取10个流量点,每个流量点重复进行3次实验,实验结果如表1所示。

表1 测试实验结果数据表

测量误差与重复性曲线如图11所示,低流量区的最大测量误差和重复性分别为-0.5%和0.4%,高流量区的最大测量误差分别为-0.9%和0.24%,根据旋进旋涡流量计检定规程要求,低流量区8～24 m3/h最大允许误差范围为3.0%,重复性小于1.0%;高流量区24～120 m3/h最大允许误差范围为1.5%,重复性小于0.5%。综合以上分析,所有指标均在规定的范围内,符合旋进旋涡流量计的性能要求。

图11 误差和重复性分布曲线图

5 结束语

本文针对旋进旋涡流量计抗干扰能力差的问题,在消除流体脉动干扰的条件下,提出了一种基于频谱分析的方法提取旋涡频率,分别对高流量区和低流量区的振动响应进行分析,结合经验模态分解与FFT方法提取频谱中幅值最大值对应的频率,规避了外部瞬态冲击振动对旋进旋涡流量计的影响,实现流量的准确测量。实验结果表明:该方案得到的测量结果符合旋进旋涡流量计行业相关标准,具有较高的实用性。