基于方式-路径模型的组合出行时空效能分析
2023-12-19于晓桦郝志良曹福锐谭佳慧
于晓桦,郝志良,曹福锐,谭佳慧
(山东建筑大学交通工程学院,山东 济南 250101)
0 引言
城市化进程的加快使城市面积和居民出行范围都在进一步扩大,单一出行模式在各方面均已无法满足居民的出行需求,组合出行模式日渐趋于主流。在组合出行中,方式和路径的选择是出行者面临的首要问题,各种交通工具有不同的行驶速度、舒适度和费用成本,并且不同的交通方式对应不同的优势出行距离和线路,都大大增加了出行者对其选择的复杂程度。组合出行方式和路径的选择机理成了众多学者研究的问题。焦峰[1]针对大型社区居民的组合出行选择行为,基于离散数学理论,运用非集计模型理论,构建了大型社区居民组合出行选择模型。张雪妍等[2]为了定量描述在不确定网络中出行者对于组合出行方式和路径的选择,引入了累积前景理论,并基于随机效用理论分析了网络随机用户的均衡条件。方瑞韬等[3]以典型的组合出行方案为研究对象,分析不同出行者方式和路径选择的标准,通过随机效用理论将出行者的选择原因定量化表达。LIU等[4]探讨了多模式网络中组合出行方式的选择机理,为了识别方式及路径选择的影响因素,建立了嵌套Logit模型,并进行时间价值估计和灵敏度分析来量化其影响程度。ZHU 等[5]提出了一种多模式广义出行费用函数,以反映组合出行方式和换乘方式对线路选择的影响,并基于C-Logit 模型,考虑了多模式容量约束和路径相关性,建立了等效于多模式随机用户均衡的非线性规划模型。于晓桦等[6]以效用最大化为原则,将多模式网络中的交通方式选择、换乘点选择和路径选择作为交通需求在各级网络的“路径”上进行分配。江成林等[7]在出行方式选择的研究中利用预约出行数据,根据方式选择的影响因素划分群体,并引入出行群体偏好系数建立考虑出行者偏好的多方式随机平衡模型。
已有的对于组合出行方式和路径选择的研究中,多数以出行者的出行效用最大化为标准,通过分析多种影响因素,构建不同的模型,以达到出行者效用最大化进行方式和路径的选择,但对于组合方式选择机理以及决策关联解析尚不充分,多数仅考虑在效用函数中加入服务水平变量,对于决策影响的考虑较少,未形成涵盖系统的建模思路[8]。组合交通方式与单一交通方式相比,最大优势在于其更倾向于公共交通方式的出行,从而提高交通系统总体效率[9],因而以出行者效用作为方式和路径的选择标准无法体现组合出行系统性的优势。HENSHER等[10]提出了以时间效能和空间效能为指标解释组合出行的优势,并指出时间效能是出行时间,空间效能是出行者在出行过程中所占的空间,一定程度体现了用户和系统两个角度对于组合出行的综合评估,但其未提出时间与空间效能的具体概念和计算方法。
文章从出行者和决策者的角度出发,以出行者的广义出行费用来代表时间效能,以路径的交通分担率来代表空间效能,建立方式划分和交通分配的联合模型,以广义出行费用和路径交通量分担率为基础,定义并提出组合出行时空效能的计算公式,将时空效能作为主要指标寻找起点-终点(Origin-Destination,OD)间的最佳组合出行路径,研究组合出行过程中所选择的方式和路径的时空效能,对于居民出行选择和城市的交通供需规划与管理均有重要意义。
1 组合出行超级网络
现在城市的交通网络规模更大、结构更复杂,各种交通方式不仅有自身独特的运行规律,交通方式之间还存在着组合关系,由节点和边组成的传统网络无法充分描述组合出行特征,而“超级网络(supernetwork)”[11]在这方面具有更大的优势,不仅能够反映交通方式自身的运行规律,还能够更好地描述不同交通方式之间的转换,现已成为处理大规模网络的主要方法[12]。
组合出行是通过换乘行为将不同的交通方式进行链接[13]。考虑到实际情况,很多组合方式在现实中发生的概率很低,如自行车和小汽车的出行组合方式,二者都能够实现点对点的出行,难以将其链接,因此文章对于此类组合不予考虑。同时在大城市出行中,以地铁为骨干,公交为补充的公共交通网络能够为出行者提供便捷的出行服务,现实中大多数组合出行通过一次换乘即可到达目的地[14]。基于一次换乘,组合自行车、小汽车、公交车、地铁4种交通方式,构建的超级网络如图1所示。

图1 交通方式组合出行超级网络图
由图1 可知,组合出行超级网络由起终点、节点、上下网弧、运行弧、换乘弧以及交通方式子网络组成。出行者从O点出发,通过步行的方式到达上网节点经上网弧进入第一个子网络,在第一个子网络内通过相应的交通方式到达换乘节点经换乘弧进入第二个子网络,在第二个子网络内通过相应的交通方式到达下网节点再以步行方式经下网弧离开子网络到D点完成出行活动。
超级网络中各交通方式在其子网络中运行,不同交通方式之间的转换由换乘弧连接,形成由节点和边组成有向网络图。如图1所示的超级网络中存在一对起终点、9 个节点、14 条边(运行弧序号:2、6、4、7、12;上网弧序号:1、9、11;下网弧序号:5、8;换乘弧序号:3、6、10、13)。超级网络的拓扑描述为G=(L,N,U,H,E),其中:L为子网络层,分别用1、2、3、4表示自行车出行、公交车出行、地铁出行、小汽车出行,l1、l2、l3、l4分别表示以自行车、公交车、地铁、小汽车在运行弧上运行,则L=(l1,l2,l3,l4);N表示网络节点集,包括自行车停放点、公交站点、地铁站点、小汽车停车场以及交叉口等路网节点,U表示网络运行弧集,与子网络层集Ui相对应,即U=U1∪U2∪U3∪U4;H表示上、下网弧集,HO、HD表示上、下网弧集;E表示换乘弧集;O为起点,D为终点;n1、n2、n3为换乘节点。
图1所示的组合出行超级网络中存在4条组合出行路径:
路径1(自行车+公交):O→(l1,n1)→(l1,n2)→(l2,n2)→(l2,n3)→D;
路径2(自行车+地铁):O→(l1,n1)→(l1,n2)→(l3,n1)→(l3,n2)→D;
路径3(公交车+地铁):O→(l2,n1)→(l2,n2)→(l3,n1)→(l3,n2)→D;
路径4(小汽车+地铁):O→(l4,n1)→(l4,n2)→(l3,n1)→(l3,n2)→D。
2 组合出行时空效能模型
2.1 广义出行费用
出行方式的选择取决于多种因素,如时间、费用、出行者自身属性等。广义出行费用将多种因素统一为货币形式,代表出行者在出行过程中所花费的成本,对路径的阻抗进行综合度量。出行者自身属性体现在反应出行时间敏感程度的“时间价值(Value of Time,VOT)”中,不同属性的出行者,对于时间价值的感知不同,如在职业方面,公职人员更注重出行时间的影响;在出行目的方面,旅行游玩者更注重出行票价等因素的影响[15]。因此,广义出行费用由出行时间和出行票价组成。为便于广义出行费研究作如下假设:
(1)各路段费用相互独立;
(2)各交通方式之间互不干扰,只存在换乘关系;
(3)上、下网以及换乘过程由步行的方式完成;
(4)小汽车换乘弧中的停车费用可用小汽车费用统一表示。
2.1.1 运行弧广义出行费用
运行弧路段上的广义出行费用包括行驶的时间和费用,其中公交车和地铁的行驶费用为票价,自行车的行驶费用由共享单车租赁费用表示,小汽车的行驶费用以高德打车平台的平均打车费用作为参考。
2.1.2 换乘弧广义出行费用
换乘弧路段的广义出行费用包括换乘节点之间的步行时间、公交车和地铁的等待时间以及小汽车的停车费用。换乘弧路段广义出行费由式(5)表示为
2.1.3 上、下网弧广义出行费用
上网弧路段的广义出行费用包括步行时间和等待时间,下网弧路段的广义出行费用只有步行时间。
2.1.4 组合出行模式下的路径广义出行费用
式中δlx为路段与路径关系,若路段x在路径l上则为1,否则为0;cx为路段x的广义出行费用,元。
组合出行的路径由一条上网弧、两条运行弧、一条换乘弧以及一条下网弧所代表的路段组成。路段出行时间包括步行时间、行驶时间和等待时间;费用包括地铁票价、公交车票价、自行车租赁费、小汽车费用。考虑到各条弧代表的路段所包含的出行时间类别各不相同,因此需要整合相同类别,并赋予权重,组合出行路径广义费用由式(9)表示为
式中m为组合出行过程中第一阶段交通方式;n为组合出行过程中第二阶段交通方式;γ0、γw、γD、γf分别为步行时间、等待时间、行驶时间、费用的权重系数;为出行方式m在路段x上的行驶时间,min;为出行方式n在路段x上的行驶时间,min;为出行方式m、n在路段x上所花费的费用之和,元。
2.1.5 广义出行费用参数标定
时间价值VOT采用国民收入计算[16],即VOT =。根据济南市统计局2021年7月6日发布的数据,2020 年济南市城镇非私营单位在岗职工年平均工资为108 391 元,法定工作日为251 d,时间价值VOT =0.9 元/min。BPR 函数中参数的标定,通常α=0.15、β=0.4。权重系数γ0、γw、γD、γf可通过协方差-层次分析法[17]标定,并通过实践检验修正,使其符合出行者选择各交通方式的实际情况。其他参数如通行能力、发车频率、运行时刻表、票价、租赁费、燃油费、停车费均已知。
2.2 方式-路径联合模型
组合出行是在出行过程中对交通方式、换乘点、路径的比较与决策,因而适合用联合模型进行分析,出行者在选择出行方式的同时完成了对出行线路的选择,从客观上为交通方式划分和交通分配两阶段的联合提供了可能[18]。
2.2.1 模型假设
为了方便模型的构建及求解做出如下假设:
(1)OD之间出行需求量已知;
(2)出行者总是选择自身认为最优的方式和线路,服从用户最优标准。
2.2.2 模型构建
方式-路径联合模型与单一交通分配模型在形式上相似,主要区别在于模型中同时存在两种交通方式,模型构建的关键在于对两种交通方式的广义出行费用进行统一,得到组合出行的广义出行费用代入到分配模型中[19]。基于组合出行广义出行费用和多路径概率分配思想的方式-路径联合模型由式(10)表示为
2.2.3 求解算法
改进的方式-路径联合模型采用连续平均法(Method of Successive Algorithm,MSA)求解,算法流程如图2所示。
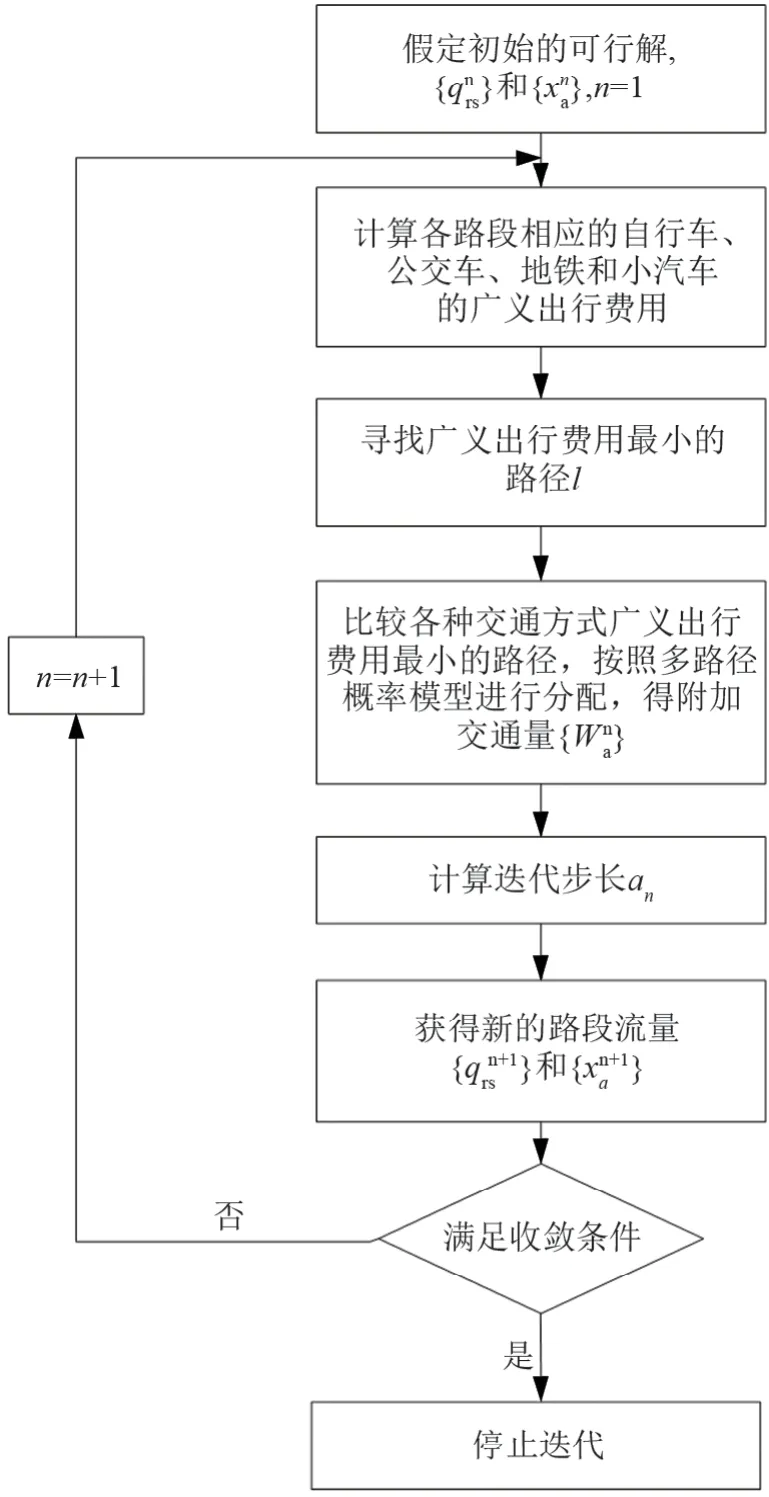
图2 MSA算法求解流程图
2.3 组合出行时空效能
组合出行时空效能由时间效能和空间效能组成,时间效能代表通过单位长度组合出行通道所花费时间和金钱的综合费用,由广义出行费用表示;空间效能代表了单位长度组合出行通道上,某一瞬间能容纳的平均乘客数,由分担率表示,广义出行费用与时空效能成负相关,分担率与时空效能成正相关,时空效能由式(11)表示为
组合出行时空效能从广义出行费用和道路分担率两个角度评价出行过程中的方式路径选择效果,广义出行费用包括出行耗费的时间和花费的金钱,与其他因素相比,时间和金钱是影响出行方式路径选择最主要的因素,因此能够代表出行者的期望准则;道路交通量的分担率表示决策者的意志,从决策者的角度总是希望所规划道路得到最大化的利用,道路所分配的交通量越大说明该道路的利用水平越高,越能够符合决策的期望准则。组合出行时空效能同时考虑到出行者和决策者两个角度,时空效能指数越高,表示该组合出行方式被选择的概率就越大,因此可将时空效能作为组合出行路径优化的有效指标。
3 案例应用分析
3.1 案例描述
以济南市山东建筑大学到洪家楼为例分析OD间组合出行时空效能,为了使组合出行的路网更加直观,将实际路网进行简化,得到如图3所示的简化路网图,各路段属性及技术特征见表1。洪家楼作为济南市的标志性地点,是大学生出行的主要目的地之一,在地铁开通之前,该OD间主要以单一模式的出行方式为主,在陆续开通地铁2、3号线以及共享单车普及后,组合出行成为主要的出行模式,考虑到不同出行距离对组合出行过程出行者出行方式的选择有较大的影响,所选择的线路由两条路段组成,不同的路段对应不同的出行距离,将<3 km 的路段视为短距离出行路段,将3~10 km视为中距离出行路段,将>10 km 视为长距离出行路段,研究所选择的7条组合出行线路见表2。

表1 路段技术特征和属性表

表2 各线路对应的路段组合和出行方式组合表
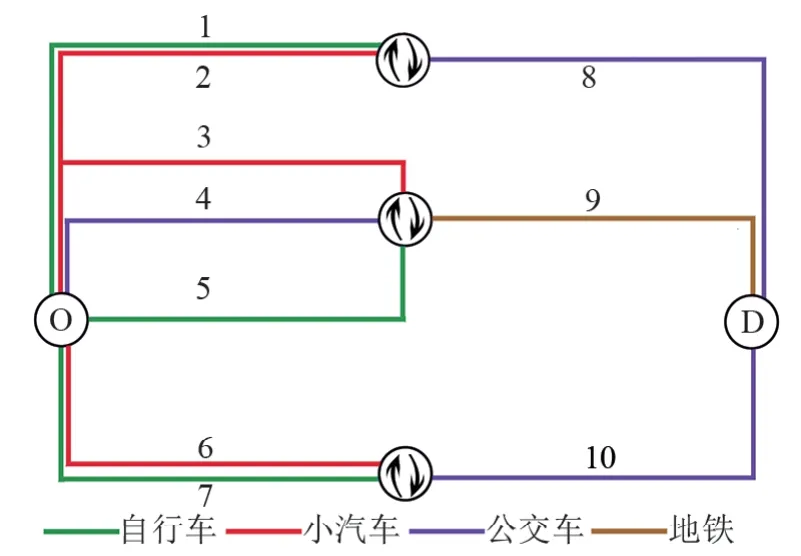
图3 组合出行简化路网图
3.2 模型参数标定和计算
采用协方差-层次分析法对各费用权重进行标定,标定结果以及一致性检验见表3、4,其中CI 为检验的一致性指标;RI 为平均随机一致性指标;CR为一致性比率,且CR =CI/RI。针对4 阶判断矩阵计算得到CI值为0.037、RI值查表为0.890,计算得到CR值为0.042<0.1,说明此次研究判断矩阵满足一致性检验,计算所得权重具有一致性。
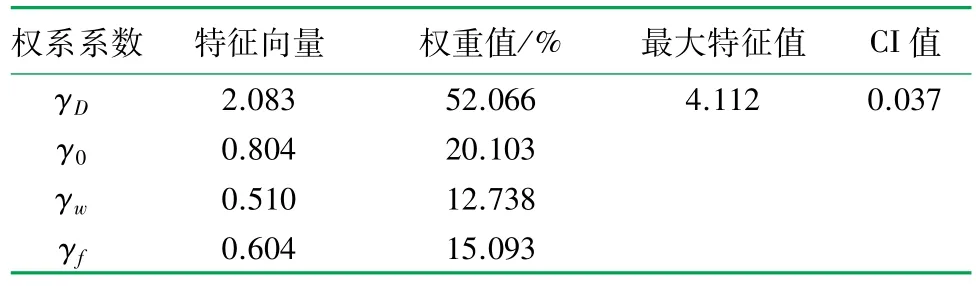
表3 协方差-层次分析结果表

表4 一致性检验结果汇总表
由式(12)计算线路广义出行费用,方式-路径联合模型及MSA 算法计算线路分担率,通过式(11)计算线路时空效能值见表5。
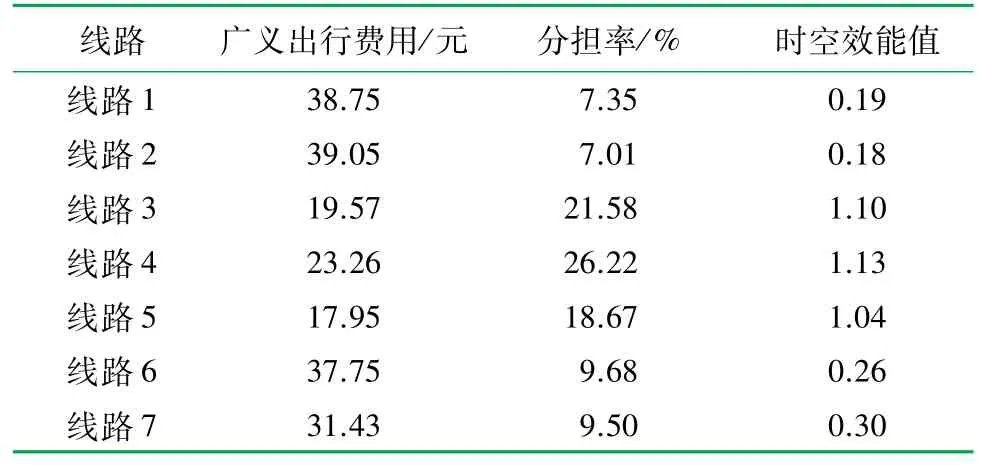
表5 线路时空效能值表
3.3 结果分析
3.3.1 短距离出行
由表2可知,线路6和7所代表的组合出行中,第一阶段均为<3 km 的短距离出行,其方式分别为小汽车和自行车出行,而第二阶段均为公交车出行,两条线路的时空效能如图4所示。
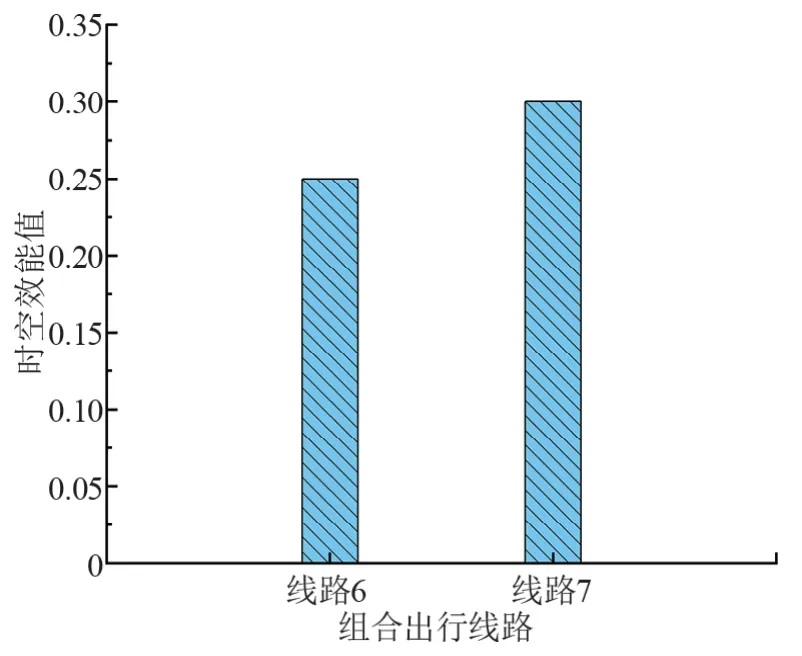
图4 第一阶段为短距离出行线路的时空效能
由图4可知,包含短距离出行的线路中,自行车出行的时空效能要高于小汽车出行,主要因为自行车在短距离出行中具有灵活、便捷和低成本的优势。
3.3.2 中距离出行
由表2 可知,线路3、4 和5 所代表的组合出行中,第一阶段均为<5 km的中距离出行,出行方式分别为小汽车出行、公交车出行和自行车出行,第二阶段均为地铁出行,3条线路的时空效能如图5所示。

图5 第一阶段为中距离出行线路的时空效能
由图5可知,包含中距离出行的线路中,公交车出行的时空效能最高,其次为小汽车出行,自行车出行的时空效能最低,主要因为自行车出行耗费体力较大且易受天气和环境状况影响,出行距离越长,该劣势会越明显。
3.3.3 长距离出行
由表2 可知,线路1、5 和2、3 所代表的组合出行中,第二阶段均为>10 km的长距离出行,出行方式分别为公交车出行和地铁出行,第一阶段的出行距离相同且出行方式分别为自行车出行和小汽车出行,4条线路的时空效能如图6所示。
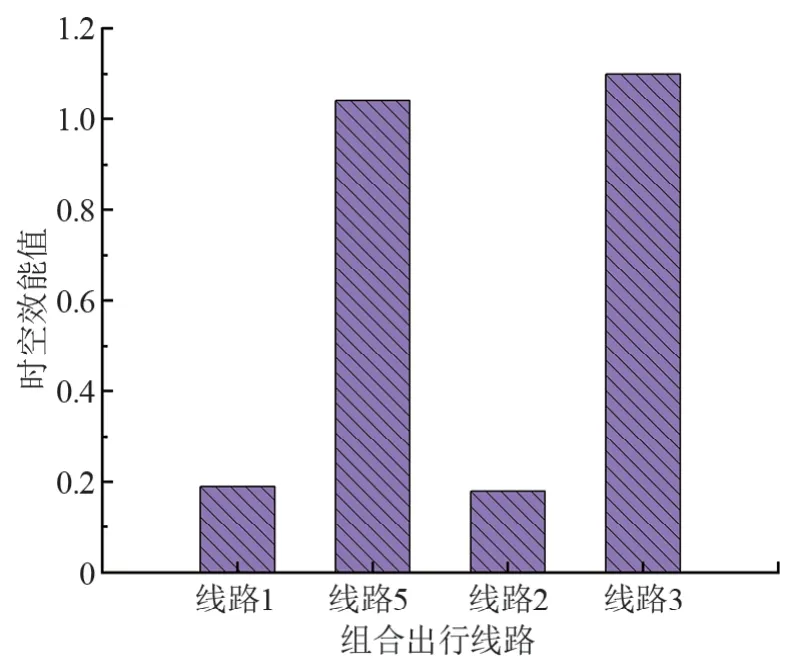
图6 第二阶段为长距离出行线路的时空效能
由图6可知,包含长距离出行的线路中,第一阶段出行方式不论是自行车还是小汽车,地铁出行的时空效能都要远高于公交车出行,主要因为在长距离出行中,地铁比公交车具有更明显的时间优势。
3.3.4 组合交通出行综合分析
所有组合出行线路的时空效能如图7所示。由图7可知,线路4 所代表的“公交车+地铁”组合出行的时空效能值最高,其最高值为1.13,线路5 和3所代表的“自行车+地铁”和“小汽车+地铁”组合出行的时空效能值较高,两者均>1.0;线路7、6、2 和1分别代表的“自行车+公交车”“小汽车+公交车”“小汽车+公交车”和“自行车+公交车”组合出行的时空效能值较低,其值均在0.1 ~0.3 之间。出行方式只有公交车的时空效能平均值为只有地铁的15%,出行方式只有公交车和只有地铁的时空效能平均值分别为同时有公交车和地铁的15%和95%。
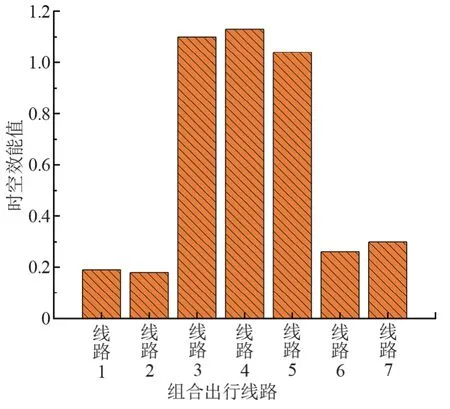
图7 组合出行线路时空效能
4 结论
根据以上研究结果可得出主要结论如下:
(1)时空效能在出行者效用最大化的基础上考虑了决策者的规划布置效果,可作为评价方式和路径选择的有效指标。
(2)方式-路径联合模型与单一交通分配模型相比,弥补了各阶段相对割裂的缺陷,能够实时动态地对广义出行费用进行标定和调整,是研究组合出行交通流分配的有效方法。
(3)以济南市山东建筑大学与洪家楼之间的组合出行线路为例,“短距离+长距离”和“中距离+长距离”的组合出行中,时空效能的高低主要取决于组合中的公共交通方式,地铁与其他3 种交通方式组合的时空效能均高于公交车的组合,且公交车和地铁组合具有最高的效能值,说明地铁比公交车具有更大的效能优势,居民在组合出行中更倾向于公共交通,该结果可为济南市公交和地铁站点设置和线路规划提供参考。
由于数据的有限性,广义出行费用的组成中只包含时间和费用因素,其他如舒适性等因素没有考虑;空间效能与多种因素相关,仅由道路交通量的分担率来表示具有一定局限性。未来将在考虑多种影响因素的基础上,研究组合出行广义费用函数的表示方法,探寻空间效能更全面的表达方式,完善时空效能的概念和优化计算方法。
