运行期土石坝渗流量分析对大坝安全影响评价

艾志娟，周清勇，熊 磊

（1.抚河河道堤防维护中心,江西 抚州 344100；2.江西省水利科学院,江西 南昌 330029）

江西省水库众多,已建成水库有10819 座,其中大中型293 座、小型10526 座,95%以上坝型为土石坝结构。水库工程对地方经济社会发展和社会稳定等均发挥了重要的作用。大坝安全监测是水库运行期的重要管理设施之一[1],是保障大坝安全的主要非工程措施,特别是大中型水库的运行管理应更为重视。大坝安全监测设施中,最直观的监测设施是在大坝下游坝脚处的集水沟设置量水堰。量水堰观测设施对于运行管理单位而言,容易观测及维护,也容易判断土石坝的运行情况。本文以大（2）型水库为例进行其运行期建模计算及回归分析。

水库[2]坐落于鄱阳湖水系赣江左岸泸水河上游,禾水二级支流东谷水支流上。坝址以上控制流域面积345.0 km2,工程为粘土心墙防渗的土石坝,大坝坝顶高程149.80 m,最大坝高67.80 m,坝顶长度290.0 m,坝顶宽度8.0 m,总库容1.26×108m3。设计灌溉面积33 万亩,电站装机16 MW,是一座以灌溉和发电为主,兼顾防洪及其他效益的大（2）型水库。工程于2015 年12 月完成单位工程的验收。目前水库已正常运行多年,主体工程运行性态还未进行安全分析,本文采用实测渗流量、有限元模型及数据统计回归模型等进行评价水库运行期的大坝安全[3-5]。

1 有限元模型分析

为真实地模拟分析土石坝运行期间的渗流稳定状态,利用多年系列观测资料选取合理的数值进行反演,以获取更为可靠的材料渗透系数。本次采用有限元法进行计算,选取运行期大坝最大断面测压管水位值对大坝坝体土层分区的渗流渗透系数进行反演[6-9],并以此进一步对大坝渗流安全进行评价。

基于饱和-非饱和渗流理论,非饱和土中渗流为随土层基质吸力变化的二阶函数,土体中体积含水率随时间变化而不同,将达西定律导入连续性方程中,采用有限元法求解渗流场的拉普拉斯控制方程如下：

控制方程的边界条件为：第一类边界为上下游水位以下的出入渗面及自由渗出段,水头为已知；第二类边界为渗流自由面和不透水层。本次采用极限平衡上限解分析,该有限元法软件由加拿大岩土软件开发商GEO-SLOPE 公司开发的面向水利、岩土、地质工程等领域开发的一套仿真分析软件。

大坝测压管断面布置图大坝典型断面见图2,本文选取桩号0+165 典型断面,坝体计算分区见图1,据断面3 个渗压计测点管水位过程线及考虑大坝常年运行下库水位而言,采用常水位即多年平均库水位137.49 m 作为渗流系数反演计算,将某时段对应的测压管水位与计算获得的浸润线进行多次对比,直至达到两者浸润线相对吻合状态,最后确定现状坝体土层中粘土心墙、上下游坝壳料层及排水棱体层等的渗透系数。本水库工程以渗压计测值正常有效以此作为反演依据,计算结果见表1,常水位下反演计算见图2,计算浸润线与测压管实测值较吻合,反演效果较理想。

表1 各分区土层有关渗透系统指标采用值表

图1 坝体计算分区图

图2 典型断面稳定渗流情况下反演计算成果图

分析可知,水库坝体防渗心墙测压管水位随库水位变化明显；大坝坝体防渗心墙上侧即坝轴线上游水位与坝轴线下游侧水位监测数据反映出心墙消减近50%的水头,防渗效果明显,且防渗心墙下侧测压管监测数据总体走势较平稳,过程线无明显突变。

土石坝运行期坝体土层材料会因蓄水上升及土体固结的影响,发生一定变形致使某些土层材料的渗透系数局部改变。本次以渗透系数反演后的参数值进行有限元计算[10],分析结果见表2 及图3。

表2 大坝坝体渗流计算及总渗流量计算估值

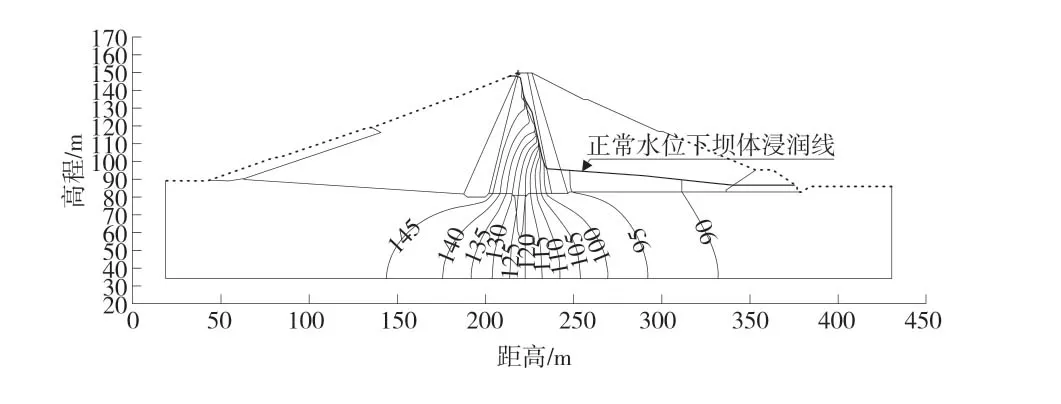
图3 正常蓄水位148.00 m 下稳定渗流计算成果图

由表2 及图3 可知,大坝浸润线在心墙上游近似呈水平分布,在心墙内呈斜线形,下游坝壳料中浸润线缓慢降落,大坝渗流计算等势线分布符合心墙渗流规律。结合笔者的现场查看,库水位136.61 m,量水堰处渗漏量约为0.75 L/s,经分析多年平均库水位137.49 m 下,计算其坝体渗流量换算值约0.82 L/s,渗流量不大且为清水,防渗效果较好,坝体发生渗透破坏可能性小。

2 渗流量实测资料分析

水库渗流量监测布置在大坝下游河床处的集渗沟处,位于大坝下游集水沟进口2.0 m 处设置的三角形量水堰,三角堰中设有水尺,采用自动结合人工读取数据。以近几年水库运行期坝体实测渗流量观测作为分析,如图4 为2015 年～2021 年的渗流量观测,观测频率为每日观测1 次,剔除连续降雨、因泄洪下游水位升高及暴雨数据不准未进行观测统计外,最大渗漏量为2016 年8 月9 日11.02 L/s,其原因是当日降雨量达到55 mm 且当日前后连续降雨,从而造成数据偏大。最小渗漏量为2020 年12 月25 日的0.57 L/s,平均渗漏量小于1.3 L/s。渗流量的大小基本与上游水位成正比。

图4 2015 年～2021 年渗流量与库水位变化过程线

由图4 分析可知,扣除个别误差外,运行期水库下游坝脚实测渗流量比本次有限元模型计算坝体总渗流量偏小,说明水库运行期大坝运行状态正常,坝体渗透稳定。

3 渗漏量统计回归模型分析

坝体渗流是土石坝主要监测项目之一。为了解水库渗流稳定运行性态,对本工程最大断面的部分渗压计所测水位与库水位等建立统计模型。大坝为粘土心墙土石材料,其渗漏量主要受上游水深、降雨入渗以及防渗体时变特性和坝前淤积等的影响,土石坝材料一般不考虑温度分量影响。

本次利用渗漏量统计模型[11-12],根据渗漏量与实际影响因子之间的相关性,可更直观地分析大坝渗漏状态。回归建模时主要考虑与上游水位的一次方和二次方、下游水位一次方、前期平均1 天、2 天、3 天水位观测值、降雨量及时效因子等,具体统计监控模型如下：

渗流量统计模型为：

式中：Q 为渗流量实测值,L/s；QH为上下游水深分量；Qp为降雨分量；Qθ为时效分量；aui为上游水深分量的回归系数；H1i为监测日上游水深m；为监测日前i 天的平均上游水深,m；m1为滞后天数；ad为下游水深分量的回归系数；H2为监测日下游水深,m；m1为滞后天数；di为降雨分量的回归系数；pi为前期降雨量,mm；c1、c2为时效的回归系数；θ为起测日开始的天数除以100；a0为参数项。

依据水库渗流量、降雨量及库水位等实测资料,定量分析典型大坝断面管水位原形观测资料,应用逐步回归分析方法,建立渗流量回归模型,即：

经分析可知,复相关系数R=0.999,标准偏差S=0.846,回归模型的精度较高,回归计算结果成果见图5。

图5 渗漏量变化过程线

由回归模型和图5 分析可知,拟合效果较理想,在对渗漏量的影响程度中,影响从大到小依次为水压分量、时效分量、降雨分量。水压分量与渗漏量关系较为显著,渗流量与库水位变化基本同步,据实测值与回归值分析过程线,渗流量呈逐渐减少的整体趋势,表明大坝整体渗透性较稳定。

4 结语

本文以水库运行期渗流监测资料为基础,对土石坝典型断面及土层参数进行了有限元和数据回归分析,主要结论如下：

1）水库常水位下,选取坝体渗压计测值作为渗流系数反演,计算出坝体浸润线与测压管实测值较吻合,反演效果理想。

2）运行期水库下游坝脚实测渗流量比有限元模型计算坝体总渗流量整体偏小,说明水库运行期大坝运行状态正常,坝体渗流量基本稳定。

3）建立渗漏量回归统计模型,可知回归模型精度较高,拟合效果理想,在对渗漏量的影响程度中,水压分量与渗漏量关系较为显著,回归过程线可知渗流量呈逐渐减少的整体趋势,表明大坝整体渗透性较稳定。