Shaping the Structural Frequency Responses with an Improved Partial Eigenstructure Assignment by Minimizing Modal Energy

-,-,-,-,-

(1.School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China;2.Mechanical and Electrical Engineering College,Hainan University,Haikou 570228,China;3.Army Military Transportation University,Zhenjiang 212003,China)

Abstract: This paper presents a new algorithm for active vibration control with both the eigenvalues and the eigenvectors designed simultaneously by multi-input feedback control.The emphasis here is placed on shaping the assigned eigenvector to reduce the structural frequency responses: (1) the subspace of the achievable eigenvectors is found with singular value decomposition;(2)the optimal eigenvectors are chosen by minimizing the modal energy;(3)the optimal eigenvectors and the desired eigenvalues can be assigned for vibration control with the proposed algorithm; and (4) a few numerical examples are given to demonstrate the effectiveness and accuracy of the proposed algorithm.

Key words:active vibration control;partial eigenstructure assignment;modal energy;optimal eigenvector assignment

0 Introduction

Over the last few decades, active vibration control engineering has attracted considerable attention and has been widely studied.The dynamic performances of vibrating systems can be described through their eigenstructures,i.e.the eigenvalues and the eigenvectors.And the eigenstructure assignment is an efficient way to improve their dynamic behavior for vibration suppression.Among the studies on the eigenstructure assignment, much attention was usually paid to the eigenvalue assignment of closed-loop systems[1-12].However, the eigenvectors also play a fundamental role in vibration response,and it is an effective way to optimize the dynamic behavior with a desired mode shape and even without introducing damping.The eigenstructure assignment which assigns both eigenvalues and eigenvectors offers a larger design space of options for vibration suppression.It was Moore[13]who introduced the eigenstructure assignment and recognized the set of possible eigenvectors using state feedback.Duan[14]proposed two complete parametric methods of eigenstructure assignment.The SVD was used for finding the basis of the null space for achievable eigenvector subspace in multi-input systems, which is a practical effective method for assigning the eigenstructure[7,15-16].Tang et al[17]achieved eigenstructure assignment by optimally selecting the achievable eigenvectors for vibration confinement.Rastgaar et al[18]proposed the orthogonal eigenstructure control for vibration confinement.Belotti et al[19]achieved eigenstructure assignment with a hybrid approach in which the mechanical system and the controller are concurrently designed to improve the attainability of the desired eigenstructure.Also it should be pointed out that the desired eigenvectors cannot be chosen arbitrarily[13,17,20].

In real active vibration control applications, usually only a few eigenvalues or partial eigenstructure are undesirable, and the rest of them remain unchanged to retain the performance of an original system.Therefore, partial eigenstructure assignment, where partial eigenvalues and corresponding eigenvectors are assigned to the desired values and the rest of them keep unchanged in a closed-loop system, is of practical value in vibration suppression.Datta[21]developed a method for partial eigenstructure assignment with the appropriate choice of gain and input matrices.Ram and Mottershead[10-11]also proposed a new theory of receptance method in active vibration control and solved the multi-input partial pole placement using partial observability.Tehrani et al[22]achieved partial pole assignment using the uncontrollability condition based on the receptance method.Zhang et al[20,23]proposed a method for partial eigenstructure assignment using acceleration and displacement feedback.Bai et al[24-25]achieved partial eigenvalue assignment using receptances and system matrices,and solved the minimum norm of the feedback matrices.Mokrani et al[26-27]recently minimized the control effort with the MIMO receptance-based controller by the numerical and experimental study.

In above-mentioned papers, one observation is that the attention is usually paid to the eigenvalues or partial eigenvalues without considering the corresponding eigenvector assignment,or to eigenstructure assignment (partial eigenstructure assignment) with eigenvectors optimized for robust or minimum norm partial eigenvalue assignment.However, the eigenvector describes the shape of system vibration and its important role in dynamic responses is not fully considered.Another observation is that a desired eigenvector is usually needed to be given a-priori, which is also very challenging from a practical point of view.Because it is difficult to determine a desired eigenvector for overall vibration suppression from the achievable eigenvectors.

To achieve partial eigenstructure assignment of vibrating structures with both the eigenvalues and the associated eigenvectors designed for vibration suppression,a new algorithm is introduced in this paper.All the parametric expressions for the improved partial eigenstructure assignment are derived in this algorithm.And minimizing modal energy in the concerned regions is applied to design an eigenvector for shaping the vibration so that they have much smaller modal amplitudes in the concerned mode and area of the structure.As a result,the optimal eigenvectors can be automatically assigned to minimize the modal energy while the eigenvalues are assigned to the desired values,both are designed to control the structural response.As the control distribution matrix affects the subspace of achievable eigenvectors, a preliminary work is done to discuss the control quantities of different actuator distribution matrices in this paper.

1 Theory

1.1 Partial eigenstructure assignment with the dynamic stiffness matrix

Consider ann-DOF vibrating system which may be described by the second-order differential equations:

wherex(t)∈Rnis the displacement vector,M,C,K∈Rn×nare, respectively, the matrices of mass,damping and stiffness.With the application of velocity-displacement feedback control, the closedloop system may be altered as

whereB=[b1,b2,...,bm]∈Rn×mis the control force distribution matrix,F=[fv1,fv2,...,fvm]∈Rn×mis the active damping gain matrix andG=[gd1,gd2,...,gdm]∈Rn×mis the active stiffness gain matrix.So the quadratic eigenvalue problems of open-loop and closed-loop systems respectively satisfy the following equations:

whereηkis a coefficient vector.It is easy to be seen that any linear combination ofmcolumns ofQk,12is an achievable eigenvector of the closed-loop system, thus the eigenvector assignment can be reduced to find a suitable vectorηk.

By substituting Eq.(11)into Eq.(8)one derives

1.2 Eigenvalue and eigenvector assignment for vibration suppression

Conventionally, the eigenvalue assignment has been considered to improve the damping or avoid resonance for reducing vibration.However,in this paper more attention will be paid to the eigenvector assignment to enable spatial control in dynamic response.In the case of multi-input system, there will be more design freedom available to shape eigenvectors for the higher dimension ofB, where the achievable closed-loop eigenvector has been shown in Eq.(11), so each choice ofηkwill lead to a different assigned eigenvector, and thus to different control gains and vibration responses.This paper aims to pre-determine an optimal closed-loop eigenvector with the desired eigenvalue being assigned simultaneously.

where a small value ofΓkcan be regarded as a weak modal vibration response under mass-normalized condition,and thekth the eigenvector is tailored to a form of overall weak responses.It can also be regarded as a small vibrational mode amplitude under a certain modal kinetic energy.When only a certain region of a structure is concerned, it may be more efficient to relocate the vibration energy from the concerned coordinates to the unimportant coordinates and the indexΓckcan be rewritten as

wherewckis a vector formed by the eigenvectorwkat the concerned coordinates,and theeis a Boolean matrix relatingwckandwk.When all the coordinates of a structure are chosen for the shaping eigenvector,e=IandΓk=Γck.

We define

In order to minimize the overall modal energy,the coefficient vectorηkshould be chosen as the corresponding eigenvector of the minimal eigenvalue ofakj.Thenηkis substituted into Eq.(16) and finally the feedback gainsF,Gare solved with Eq.(17).

2 Numerical examples

In this chapter,we present three numerical examples to show the effectiveness of the proposed algorithm,and the shaped structural frequency responses are also shown in the examples.

Example 2.1 Consider the following four degree of freedomM,C,Ksystem[28]：

The open-loop eigenvalues are:

λ1,2= -0.0108±0.8736i,λ3,4= -0.0809±1.6766i,λ7,8= -0.3980±4.0208i (25)

For simplicity but without loss of generality, we wish to replace eigenvaluesλ1,2withμ1,2=-0.0054±1i while keeping the other eigenvalues unchanged.In this example, the value of the imaginary part has been increased slightly and the real part has been halved,so a small damping is chosen deliberately, which usually results in a sharp peak.However, the reason for this choice is that we want to validate that the responses can also be reduced with an improved eigenvector assignment even with a decreased damping.

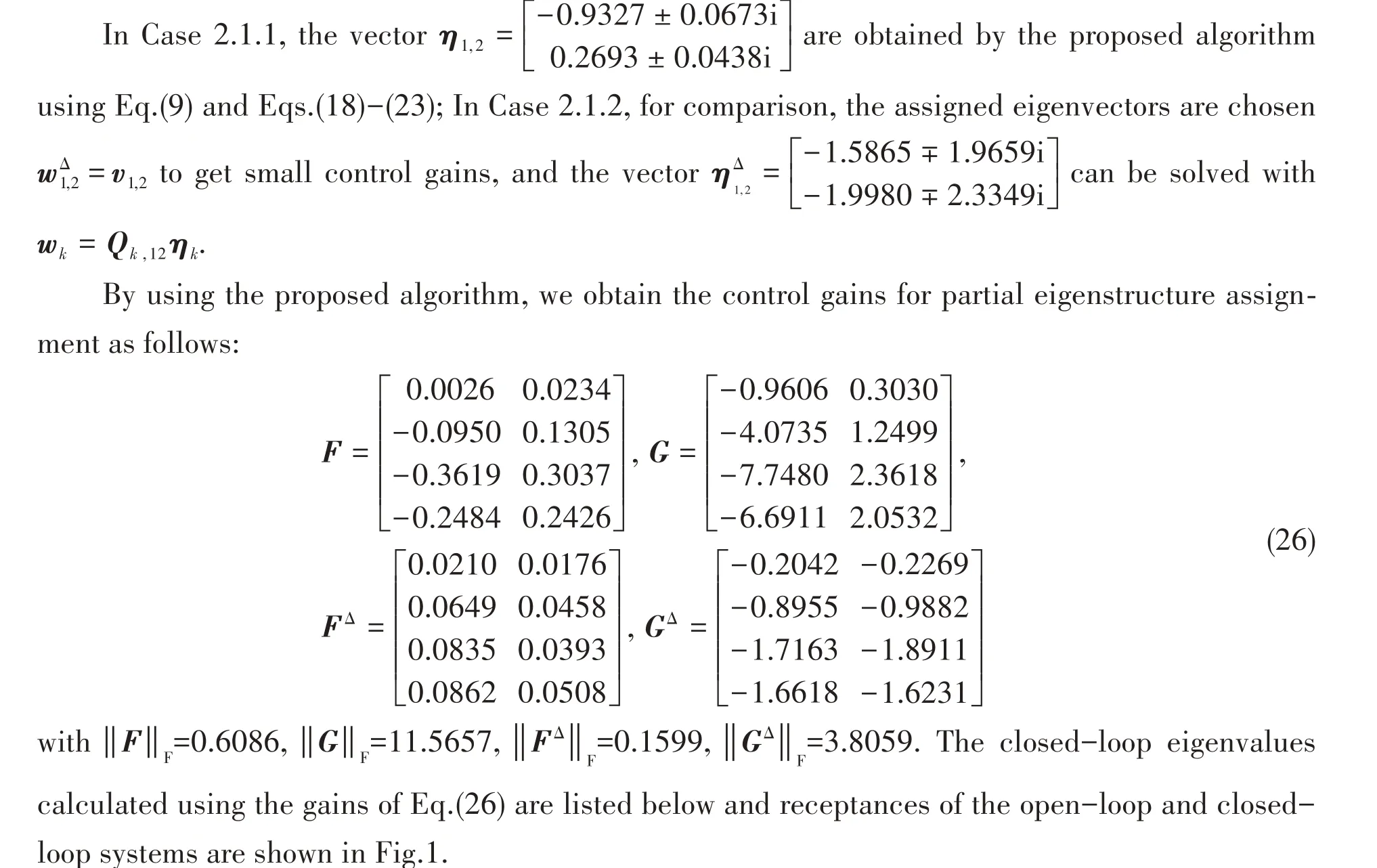
Fig.1 Receptances of the open-loop and closed-loop system in Example 2.1

The listed eigenvalues show that the first pair of eigenvalues are assigned successfully to the prescribed values,while the other eigenvalues are kept unchanged in this example.The results firstly validate that partial eigenvalue assignment can be achieved with the proposed algorithm.Fig.1 shows the receptances of open-loop system as in dashed (blue) lines, the receptances in Case 2.1.1 as in full(red)lines and the receptances in Case 2.1.2 as in full(green)lines.Although the eigenvalues are assigned to same values in the examples, their responses are different as the different assigned eigenvectors.It is shown in Fig.1 (H11-H24) that the first peaks in Case 2.1.1 are suppressed more largely than those in Case 2.1.2.Furthermore, as the first assigned modal damping is smaller than that of the original system,the responses usually increase just as the receptances in Case 2.1.2.However, comparison of the blue lines with the red lines in Fig.1 shows that the first peaks have been reduced largely, demonstrating the important role of the assigned eigenvector in effective control of the dynamic response.It should also be noted that the norms of feedback control gains are larger than the values of Case 2.1.2, which means that vibration still can be reduced by reassigning the first eigenpair at the cost of more control effort.

Fig.1 also shows that not every peak has been suppressed in the optimized assignment (e.g.,H33andH44in Fig.1).The results can be explained with the assigned eigenvectors of closed-loop system.Fig.2 shows the amplitudes of eigenvectors of the open-loop and closed-loop systems.It is shown that the first eigenvector has been assigned and unassigned eigenvectors are almost parallel to the eigenvectors of the open-loop system.In Case 2.1.1, the eigenvectors are optimized to minimize the modal energy, and it can be observed in Fig.2 (Mode 1) that elements of the eigenvector are altered to smaller values, especially Node 1 and Node 2, their values are close to 0 so that the receptances in Fig.1 (H11-H24) are largely suppressed.It is also observed that the values of Nodes 3 and 4 are not reduced so that the first peaks inH33,H34,H44of Fig.1 have not been suppressed in this case.

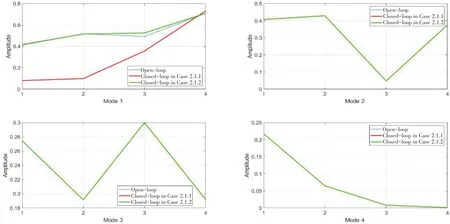
Fig.2 Eigenvectors of the open-loop and closed-loop systems in Example 2.1

However,it is worth noting that the first mode shape has been changed for minimizing the overall energy and the vibration levels have been effectively suppressed with this partial eigenstructure assignment.It also should be reminded that the damping of the first mode in this example has been assigned a small value for illustrating the great effect of eigenvector on shaping the vibration response.In practice, the damping is usually increased in the passive or active control.So, the desired natural frequencies,the large dampings and the optimized eigenvectors can be simultaneously assigned with the proposed algorithm for a better vibration control,and they will be shown in the following examples.

Example 2.2 Consider again Example 2.1, where theλ1,2are changed toμ̂1,2= -0.0432±1i with a large real part of eigenvalues and a discussion is done with the different actuator distribution matricesB.The control gains are listed in Tab.1 while the receptances are shown in Fig.3.

Tab.1 Control gains with different actuator distributions

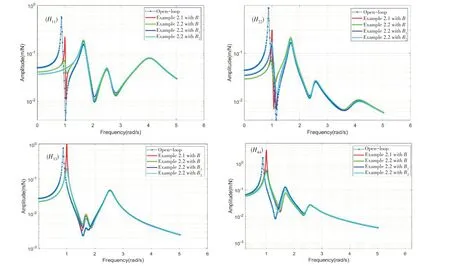
Fig.3 Receptances of H11,H22,H33 and H44 with different actuator distributions

It is found that the desired eigenvalues can be assigned precisely in all the cases,however,the control gains and the corresponding receptances of closed-loop system are different.Comparing the receptances of the assignedμ1,2= -0.0054±1.0000i (Example 2.1) andμ̂1,2= -0.0432±1.0000i(Example 2.2) in the actuator distributionB, it can be observed that the first peaks ofH11,H22,H33andH44in Example 2.2 are much lower than in Example 2.1 and the open-loop system, which shows that the eigenvalue and eigenvector simultaneous assignment can considerably reduce the vibration level of the system.Comparing the receptances of Example 2.2 with the actuator distributionBandB1, although the number of actuators is the same, the different responses ofH11andH22are obvious, which can be explained with the different optimal eigenvectors from the different actuator distribution.As for the case withB2,although there is a greater number of actuators thanB1,the differences in close-loop receptances are not significant, moreover, the values in control gainG2are larger than the others.These results indicate that the greater number of actuators may not result in the better vibration suppression and the different locations of actuator may result in the different control results.It also indicates that when the local responses are concerned (eg.H11withB1), more attention should be paid to the actuator numbers and locations.

Example 2.3 Consider a discrete shear beam system in the multiple-input control system withn=10 andm=6,where

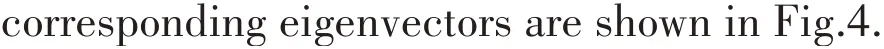
It is found that the desired eigenvalues can also be assigned precisely in the examples,and the eigenvectors have been reassigned in Case 2.3.1 and Case 2.3.2.It is observed from Fig.4 that the values of two concerned coordinates have been assigned to almost 0, and they become the vibration nodes in the assigned modes, which means that the responses involving the concerned coordinates will be greatly reduced in the range of concerned frequencies.

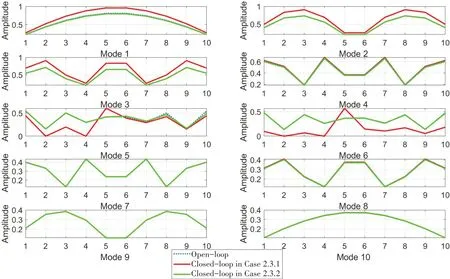
Fig.4 Eigenvectors of the open-loop and closed-loop system in Example 2.3

The receptances that involve the second and fourth coordinates are also shown in Fig.5.It can be found that the responses in Case 2.3.1 are much lower than the results in Case 2.3.2 and in the open-loop system,especially near the range of assigned frequencies,which can be explained by the reassigned eigenvectors and eigenvalues.However,its feedback norms are larger than the results in Case 2.3.2.Because the eigenvectors are chosen to minimize the feedback norms in Case 2.3.2 and the eigenvectors are chosen to minimize the vibration responses in our algorithm.It should also be noted that there are some height changes of peaks, which may result from the changed left-eigenvectors,and the changes will be discussed in another work.

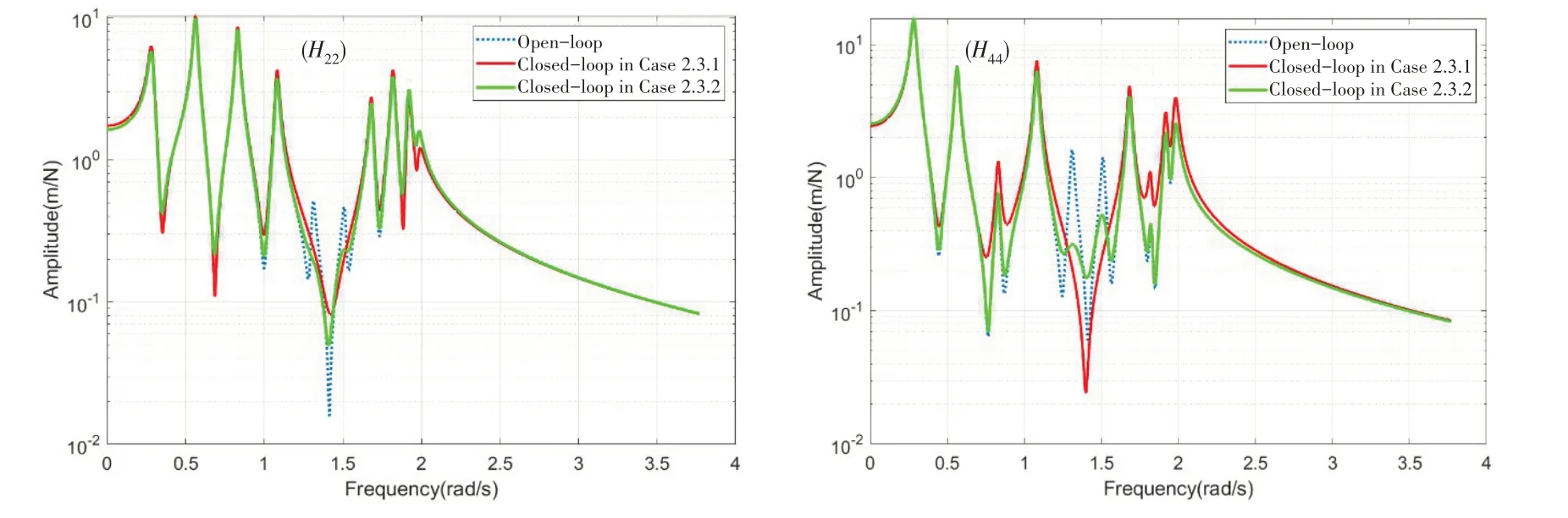
Fig.5 Receptances of Example 2.3:H22 and H44

Example 2.4 A simply-supported steel beam shown in Fig.6 is considered and it has been numerically and experimentally studied by eigenvalue assignment[30].

Fig.6 Model of a simply-supported beam

In this example, the first pair of eigenvaluesλ1,2= -2.23±446.53i will be replaced withμ1,2= -8.8±446.53i and the other eigenvalues are kept unchanged.Three positionsA,BandC(node number:2,5,8)are concerned in the control system.

In this example, the first pairs of eigenvalues and the concerned node amplitudes in the assigned eigenvector have been assigned to reduce the responses of the beam.And the results can be illustrated in Fig.7 and Fig.8.Fig.7 shows the eigenvectors of the open-loop and closed-loop system.It can be found that the values of Nodes 2, 5 and 8 are assigned to nearly 0 in the first mode and the other modes remain largely unchanged.So the responses of the concerned positions are much lower than the results with the method in Ref.[27] and in open loop system, especially near the range of the first natural frequency,which have also been shown in Fig.8.

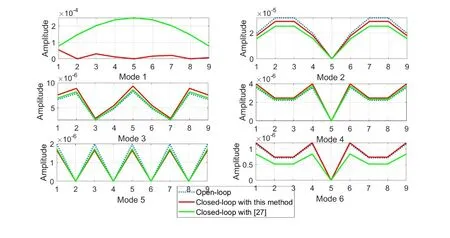
Fig.7 Eigenvectors of the open-loop and closed-loop systems in Example 2.4

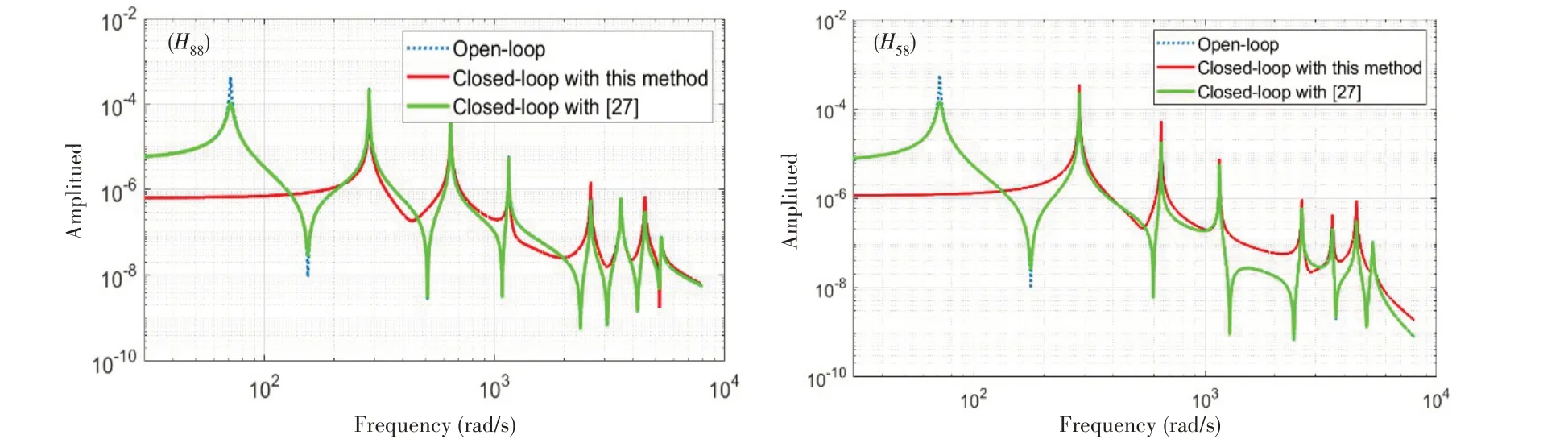
Fig.8 Receptances of Example 2.4:H33 and H55,H88 and H58

3 Concluding remarks

This paper presents a new algorithm for partial eigenstructure assignment with both the eigenvalues and the associated eigenvectors designed simultaneously for vibration suppression, which can not only assign the desired eigenstructure accurately with other eigenstructures kept unchanged,but also reduce the responses of the concerned regions by minimizing the modal energy of the reassigned modes simultaneously.The optimal eigenvectors are chosen for minimizing the modal energy, so no predetermined eigenvectors are needed in the developed algorithm.Numerical results show the significant role of eigenvector in responses and demonstrate the efficiency of the algorithm.Also, the control quantities of the different actuator distribution matrices have been examined in this study, the results show that the greater number of actuators may not result in the better vibration suppression and different locations of the actuators may result in different control results.It should also be noted that much control effort may be required for tailoring the eigenvectors, and that it is acceptable that more effective control can be achieved with this algorithm,however.