Load-bearing Characteristic Analysis of Marine Sandwich Composite Structures with Bi-modulus
2023-12-19-,-,-,-,
-,-,-,-,
(1.Key Laboratory of High Performance Ship Technology(Wuhan University of Technology),Ministry of Education,Wuhan 430063,China;2.School of Naval Architecture,Ocean Energy Power Engineering,Wuhan University of Technology,Wuhan 430063,China;3.Marine Design&Research Institute of China,Shanghai 200011,China)
Abstract: Sandwich composites are widely used in marine structures due to their excellent comprehensive properties.However, the load-bearing characteristics analysis of marine sandwich composite structures faces challenges due to the different elastic moduli in tension and compression.Based on the modified Reissner theory assumptions, the governing equations for the deflection of rectangular sandwich plates with different tensile and compressive moduli are deduced,and the theoretical approximate solutions of simply-supported rectangular sandwich panels under uniform load are presented.Furthermore, based on the proposed material model with unequal elastic moduli in tension and compression, a finite element analysis model considering bi-modulus suitable for complex marine structures is established.Numerical example results show that the theoretical model and numerical method proposed in this paper have a high computational accuracy.The relevant calculation methods can serve as a reference for the structural design and numerical simulation of complex sandwich composites with bi-modulus.
Key words:sandwich composite;bi-modulus;modified Reissner theory;deflection control equation;numerical model
0 Introduction
Sandwich composites are widely used in marine engineering because of their excellent comprehensive properties.At present,the proposed theoretical models used for the bearing capacity analysis of sandwich composites mainly include Reissner theory[1],Hoff theory[2]and Ching-Hua theory[3].Most of these theoretical models consider that the sandwich plate mainly depends on the panel to resist bending,while the core material mainly bears the transverse shear force,which is a kind of theories for sandwich plates with soft core,without considering the unequal tension and compression of elastic modulus.
Numerous experimental studies have shown that most engineering materials, such as concrete,rock materials, plexiglass, rubber, ceramics and composites, have different modulus properties in tension and compression[4].For carbon fiber, the stiffness difference between tension and compression can be as much as 100% to 400%.These materials with different properties of tension and compression are called bi-modulus materials[5].In order to meet higher functional requirements, the composite materials are designed into honeycomb sandwich structure and foam sandwich structure with reinforcing ribs, as shown in Fig.1.Conners et al[6]also pointed out that the tensile modulus and compressive modulus of different composite structures are quite different.For example,the tensile modulus of glass fiber panels based on epoxy resin is about 1.25 times of the compressive modulus.The tensile modulus of carbon-carbon composite laminates is about 2 to 5 times larger than the compressive modulus, and the tensile modulus of various fabric-rubber composites is about 2 to 14 times larger than the compressive modulus.Zhao et al[7]calculated the three-point bending beam whose tensile elastic modulus is 10 times larger than compressive elastic modulus.The study found that the maximum calculated stress in the middle span of the beam with equal tensile and compressive modulus of materials was only about 0.5 times larger than that with different tensile and compressive modulus of materials,and the deflection in the middle span of the beam was also quite different.Therefore, in the structural analysis of composite materials,the effect of different elastic modulus on tension and compression needs to be considered.
Due to the complexity of the problems with different moduli, only a few geometrically simple problems with different modulus in tension and compression can be solved analytically, such as beams and columns[8-9].Many researchers are devoted to solving the bending of anisotropic laminated plates with different modulus characteristics in tension and compression[10-12].He et al[13]proposed a simplified mechanical model of isotropic thin plate bending with different modulus characteristics in tension and compression based on the classical Kirchhoff hypothesis.In the model, it was assumed that the thin plate had a neutral surface,and the thin plate was divided into two different regions:tension and compression.Ma et al[14]renewed the bending control equations of rectangular sandwich plates with different modulus, considering only the unequal tension and compression of elastic modulus of the core.To sum up, for the bending problem of plates with different modulus in tension and compression, the current research mainly focuses on anisotropic laminated plates and isotropic thin plates, and there is little research on sandwich plates.In calculating sandwich composite structures,they are still considered as a single modulus material,without considering the influence of different elastic modulus in tension and compression.Therefore,it is necessary to solve the problem of unequal tension-compression elastic modulus of sandwich composite structures theoretically and numerically.
In this paper, the deflection governing differential equations of rectangular sandwich plates with different elastic moduli under uniform loads are derived and solved.Based on the proposed material model with an unequal tensile and compressive elastic modulus, a finite element analysis model considering different tensile and compressive moduli is established.The results show that the theoretical and numerical method proposed in this paper has a high calculation accuracy and is convenient for engineering application.
1 Theoretical basis of bi-modulus analysis
1.1 Revised Reissner theory
The calculation model of rectangular sandwich panels is shown in Fig.2.The length of the rectangular model isaand the width isb.And the thickness of the panel and core material aretandhcore, respectively.Assuming that there is a neutral surface in the sandwich panel under the transverse uniform load, the neutral surface divides the sandwich panel into two parts: tension and compression.Thexyplane is located in the neutral surface,the side panel withz>0 is the upper panel,and the side panel withz<0 is the lower panel.
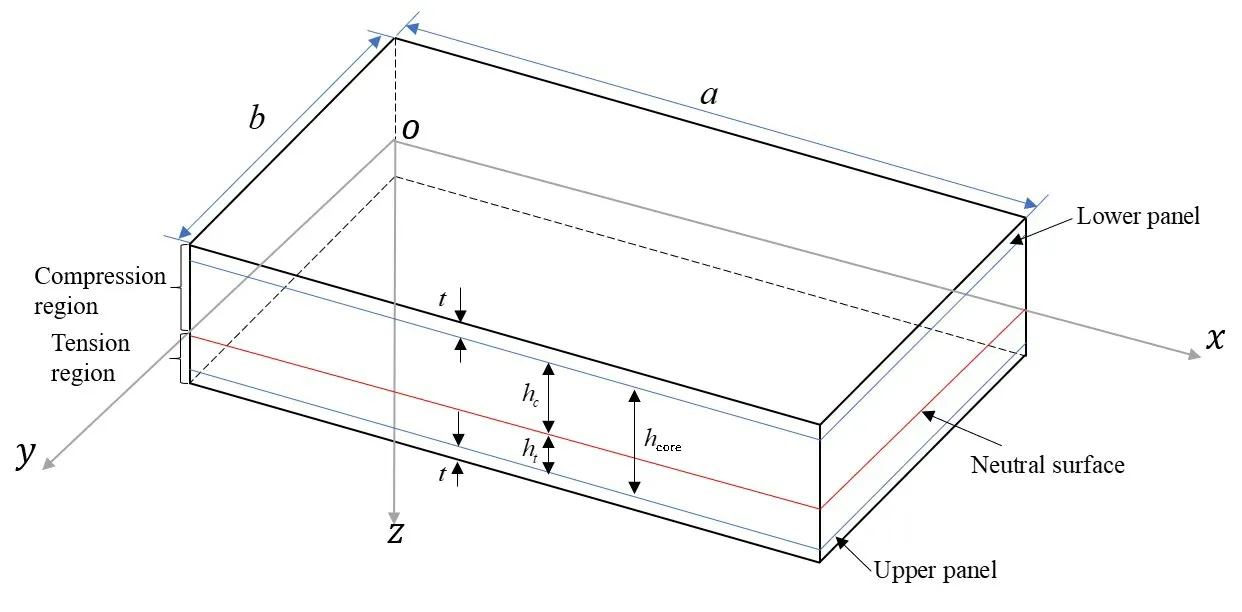
Fig.2 Calculation model of bi-modulus sandwich panel
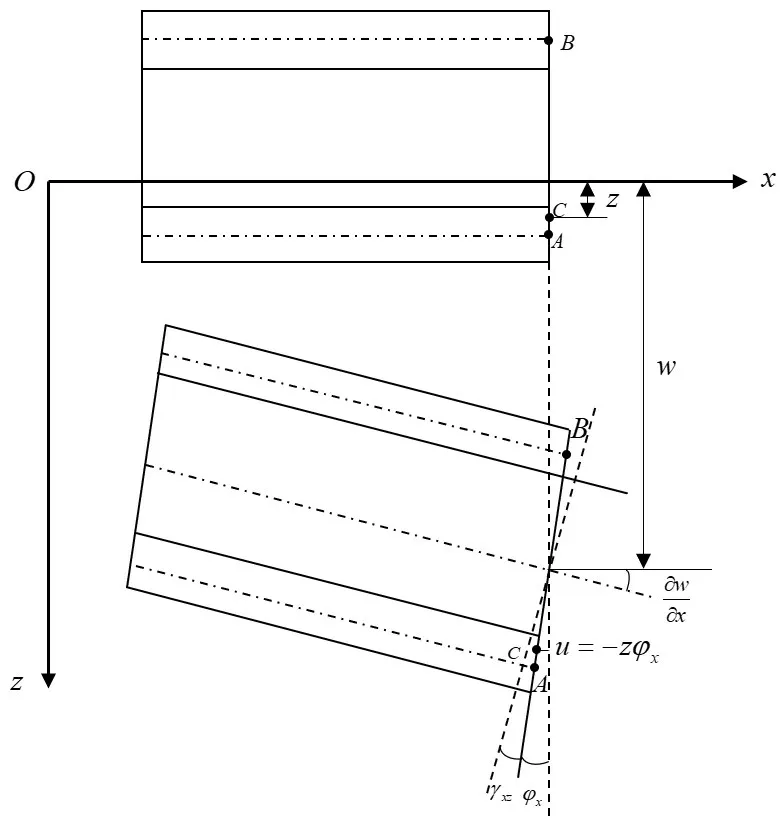
Fig.3 Schematic diagram of bending deformation of sandwich panel
In the traditional Reissner assumption, the panel mainly bears the bending load and the core material mainly bears the transverse shear load.In the revised Reissner sandwich theory adopted in bi-modulus analysis in this paper,the core material bears not only the transverse shear load but also the bending load.
1.2 Control equation
1.2.1 Geometric equation
Under the above basic assumptions, the displacement of the sandwich panel is shown in Fig.3, whereAandBare the midpoints of the upper and lower panels respectively,andφxis the rotation angle after the deformation of the line segmentAB, which specifies that the rotation from thexaxis to thezaxis is the positive direction of the rotation angle.
Upper panel:
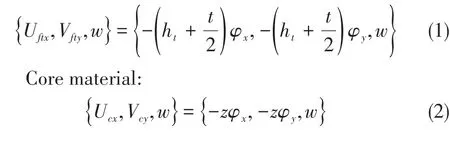
Lower panel:
wherehtandhcare the compressive thickness and tensile thickness of the core material respectively.
The strain results of each part are as follows:

1.2.2 Physical equation
Considering the unequal tension and compression of sandwich panel elastic modulus,the elastic modulus of the upper panel and the elastic modulus of the lower panel areE1=E2=EftandE1=E2=Efcrespectively.The elastic modulus of the core material in the tensile area isEct,and in the compressive area isEcc,as shown in Fig.2.
Upper panel bearing tensile:

Similarly,the stress of lower panel and compression zone of core material can be obtained.
1.2.3 Neutral surface
Under the action of transverse load,the resultant axial internal force of the cross section of sandwich panel is zero:
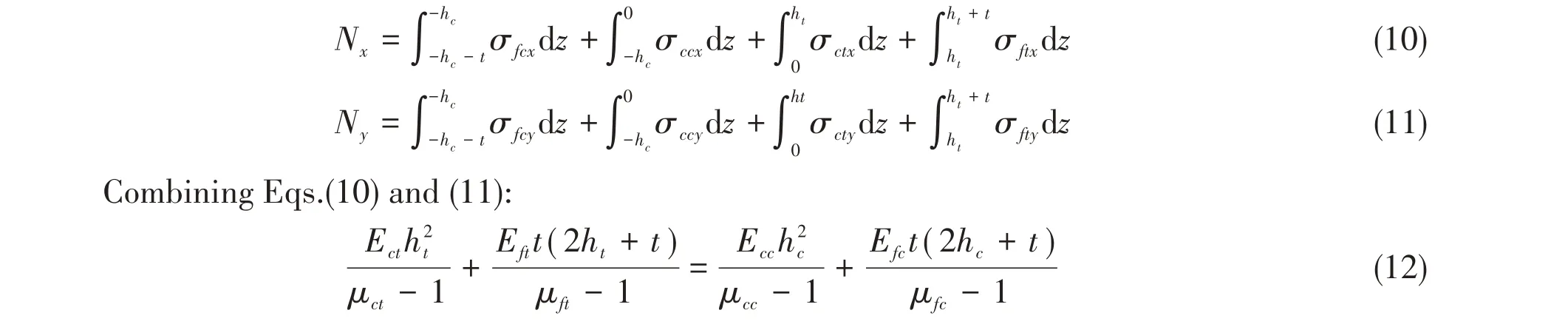
Combined with the known conditionsht+hc=hcore, the position of the neutral surface can be determined.
1.2.4 Bending differential equation
The bending differential equation is derived by using the principle of virtual displacements:
whereδUftis the virtual work done by the internal force of upper panel,δUfcis the virtual work done by the internal force of lower panel,δUctandδUccare the virtual work done by the internal force of core material in the tensile zone and compression zone respectively,andδVis the virtual work done by the external force.The Euler-Lagrange equations are:

2 Bi-modulus simulation numerical method
The above analytical solutions are only applicable to sandwich composite materials with simple structures or loads.For complex structures,the corresponding numerical methods need to be further developed.Based on the principal stress components, Ambartsumyan et al[5]put forward an elastic theory for mechanical analysis of bi-modular materials and structures.It is worth emphasizing that Ambartsumyan's model is based on the assumption ofμ+/E+=μ-/E-.For the case ofμ+/E+≠μ-/E-,Jones[15]proposed a material correction model.
Due to the coupling between the elastic matrix and the principal stress state, the actual solution process of the Ambartsumyan model is characterised by slow convergence speed and instability of iteration process.Pan et al[16]developed an improved tension-compression elastic modulus calculation program with fast convergence speed and stable results, but the case ofμ+/E+≠μ-/E-is not considered.Xie et al[17]extended the material correction model proposed by Jones[15]to the three-dimensional stress state when analyzing the problem of bimodular orthotropic materials,and used it to analyze the structural response under the complex stress state whenμ+/E+≠μ-/E-.On the basis of Xie's method, the finite element numerical model of different modulus under tension and compression in a complex stress state is established in this paper,which can be applied to the calculation of sandwich composite structures.In the principal stress coordinate system, the stress-strain relationship of the material is as follows:
For 3D solid structures:
For 2D plate structures:
For 3D solid structures, according to the combination of stress states of principal stress, different tensions and compressions can be divided into two types: the first type area, with the same stress states in three directions.In the second type area,the normal stress in one of the three directions is different from that in the other two directions.As shown in Tab.1,there are altogether eight combinations.

Tab.1 Positive and negative combination of three principal stresses
Under the principal stress coordinate system,the specific constitutive relation is as follows:
(1)Whenσ1>0,σ2>0,σ3>0:
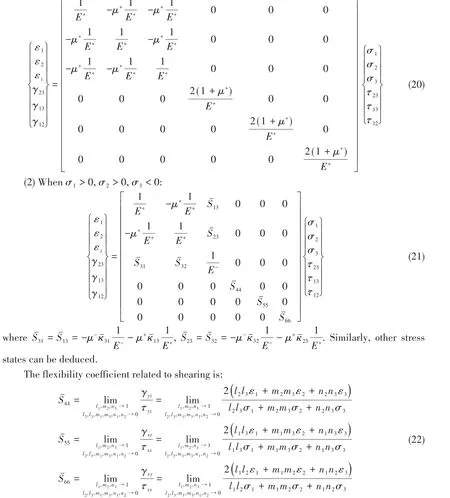
whereli,mi,ni(i= 1,2,3) are the directional cosines of the principal stressesσ1,σ2,σ3with respect to the global coordinatesx,y,z.The flexibility coefficients under 8 principal stress states can be obtained in Tab.A1 of Appendix A.
For 2D plane structure,
In the finite element numerical calculation, we have compiled corresponding Abaqus/Standard subroutine for 3D structures and 2D plane structures respectively to realize the above process,and the calculation flow is shown in Fig.4.
3 Method validation
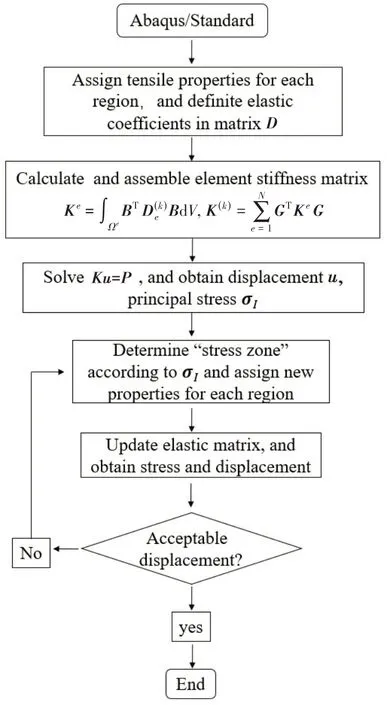
Fig.4 Iterative calculation flow of different modulus in tension and compression based on Abaqus UMAT subroutine
Fig.5 shows the finite element numerical solution and theoretical approximate solution of the deflection at the symmetry plane (y=0)when the sandwich panel and core materials are all calculated according to the tensile modulus and compressive modulus.Compared with the finite element numerical solution,the maximum relative errors of the theoretical approximate solution are 8.7% and 4.7%, respectively.As shown in Fig.6(c), the theoretical approximate solution of deflection and the finite element numerical solution have a relative error of about 0.2%.The above examples have verifed the effectiveness of the theoretical and numerical methods in this paper.
3.1 Validation of sandwich composite panel
The calculation model of sandwich panel isa=2000 mm in length andb=2600 mm in width.The panel thickness and core material thickness aret=2.5 mm andh=34 mm respectively.Sandwich panels are simply supported around and subjected to uniform pressure withP=1 kPa.The material parameters of sandwich panels are shown in Tab.2.
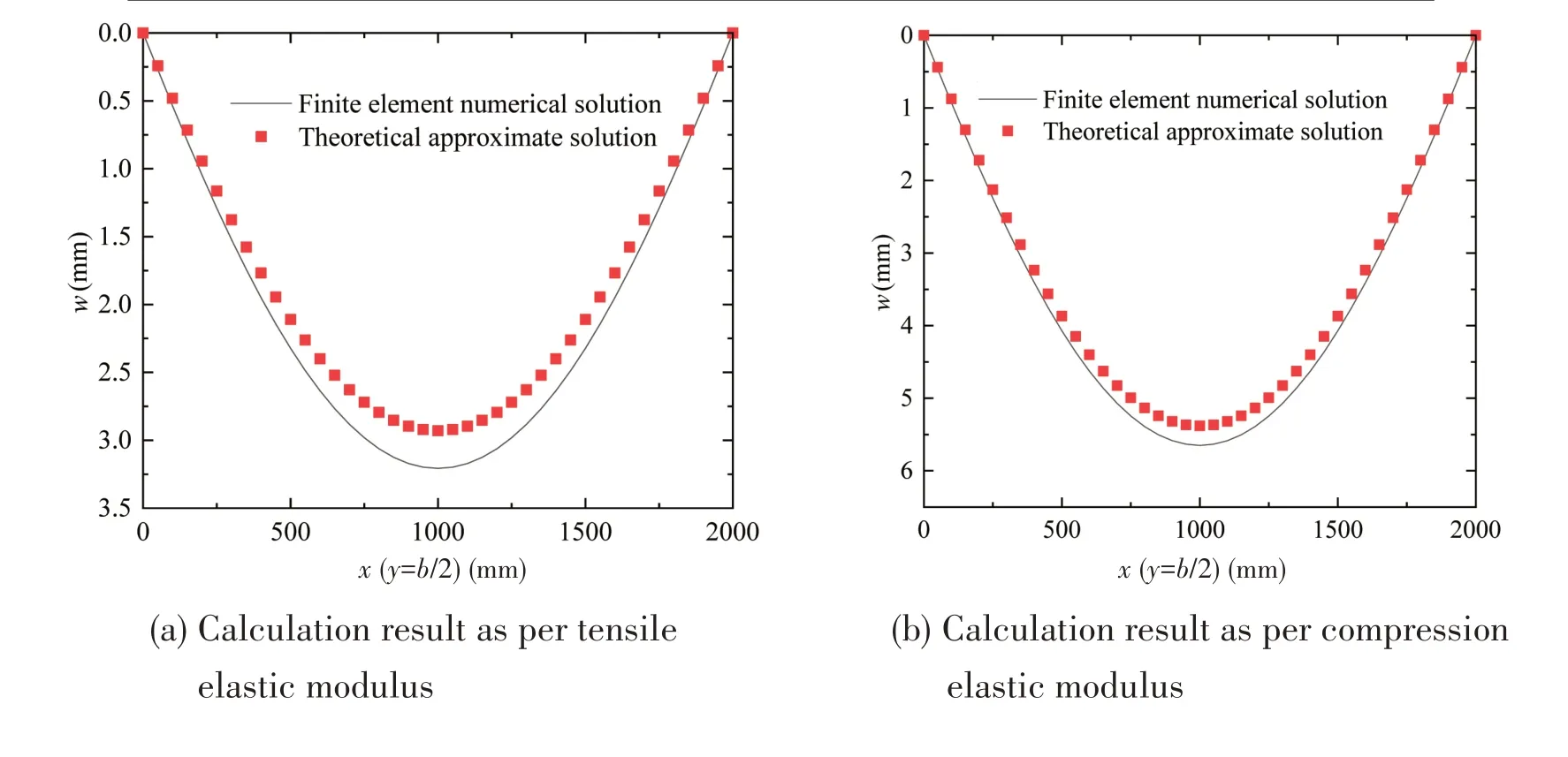
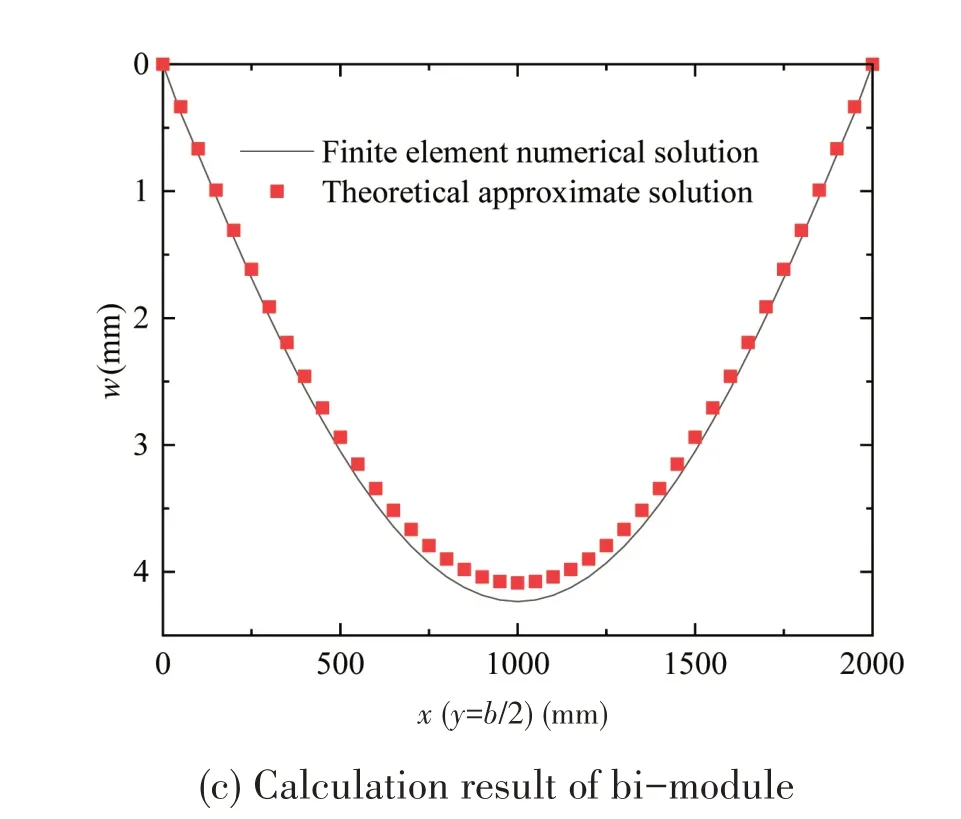
Fig.5 Deflection curve at symmetrical plane
3.2 Verification of marine composite cabin

Tab.3 Material properties of marine composite cabin

Fig.6 Sandwich cabin structure
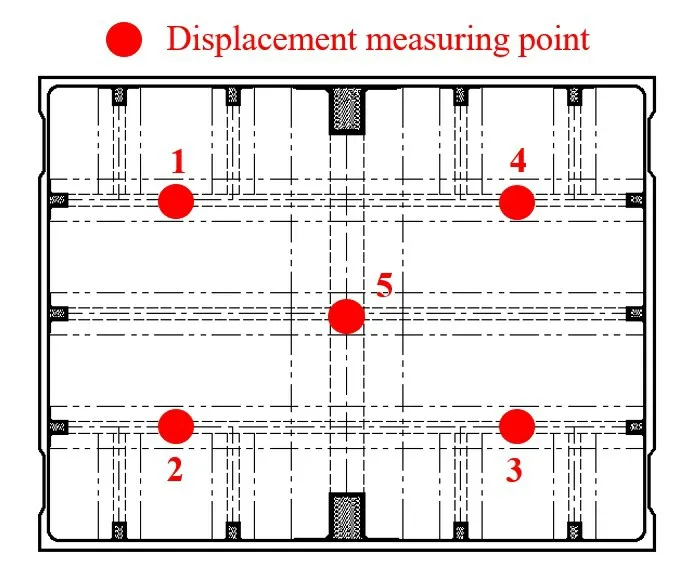
Fig.7 Arrangement of displacement monitoring points
Based on the finite element software ABAQUS, the model is established with the cabin center as the coordinate origin.TheXdirection is the length direction and theYdirection is the width direction.Considering that the structural model is large, the FRP panel of the sandwich structure is thin and needs to be provided with multiple layers.The global use of three-dimensional solid elements in the model will lead to more elements and longer calculation time.Therefore, SC8R and C3D8 elements are respectively used to simulate the panel and sandwich of the composite sandwich material, and the mesh size is 10 mm×10 mm×3 mm.The Composite Layup tool in ABAQUS is used to set up the panel in layers, with a total of 10 layers.The unequal tensile and compressive modulus of materials are realized by calling the compiled UMAT subroutine.The experimental measurement results and finite element calculation results of each monitoring point are shown in Tab.4.According to the calculation results,it can be seen that the calculation results considering different tensile and compressive properties of materials are similar to the experimental measurement results,and the error between the calculation results and the experimental measurement values considering different tensile and compressive modulus of other measuring points is basically 6%, except for Measuring Point 4.However, the calculation result based on the compressive modulus is more than 30% larger than the experimental measurement results,and the calculation result based on the tensile modulus is about 16% smaller than the experimental measurement value, showing that the calculation method considering the unequal tensile and compressive modulus of materials in this paper is suitable for complex large structures,and that it is necessary to consider the different tensile and compressive modulus of materials when calculating sandwich composite materials.
4 Conclusions
The following conclusions can be drawn:
(1)The bending control equation of sandwich panels considering the unequal tension and compression of elastic modulus of panel and core material was derived, and the theoretical approximate solution under the uniform load of simply-supported boundary was presented.Moreover, the finite element numerical analysis model considering bi-modulus suitable for complex marine structures was established, and the theoretical approximate solution was compared with the finite element numerical solution.
(2)Numerical example shows that the unequal elastic modulus in tension and compression has a great influence on the section characteristics and load-bearing characteristics of sandwich panels.If the influence of bi-modules is not considered, the error of deformation results on cabin structure is as high as 30%.
(3) The bi-modulus numerical method proposed in this paper is extended to predict the displacement field and stress field of the complex sandwich composite cabin structures.The results show that the relative error between the numerical prediction results and the measured data is within 6%,which verifies the effectiveness of the numerical method.
Appendix A

Tab.A1 Flexibility coefficients in principal stress coordinate system

Tab.A1 (Continued)
杂志排行
船舶力学的其它文章
- Experimental Study on Generation and Evolution of Three-dimensional Freak Waves
- A Numerical Study of Wave-Structure Interactions for a Square Structure with Different Submerged Depths
- Numerical Simulation of Two Degrees Coupled Sloshing of Distributed Liquid Tanks in Ships
- Freezing Process Simulation of Standing Water Droplets Under Different Supercooling and Contact Angles
- Analysis on Plastic Responses of Metal Foam Sandwich Beams under Low Velocity Repeated Impacts
- An Improved Prediction Method for Structural Response Analysis of Offshore Wind Turbines
