基于GMS模拟预测云南保山盆地孔隙水中氨氮的迁移规律

2023-12-18杨加明徐世光李胜张佳慧

地质灾害与环境保护 2023年4期

杨加明,徐世光,2,李胜,张佳慧

(1.昆明理工大学国土资源工程学院,昆明 650093;2.云南地矿工程勘察集团公司,昆明 650011;3.云南南方地勘工程有限公司,大理 671000)

1 引言

水资源是人类生存生活及生产所必备的条件,尤其是地下水资源对人类的生存和发展具有助力作用,地下水是我们人类及部分物种赖以生存和整个社会发展的前提基础,是经济社会可持续发展和生态系统循环的最基础的物质[1-2]。近些年地下水污染问题显得日渐突出,为了促进经济的发展,工业的飞速发展,造成地下水污染现象明显[3-4]。地下水开发利用过程中存在正常水位出现明显下降、地面沉降、水质状况恶化等重要问题[5]。王攀[6]等人对永城市浅层地下水中污染物的来源作了解析,导致该区域中硝酸盐和硫酸盐超标的主要来源是工业污水排放,农业农药和化肥的过度使用;李政红[7]等人探究人类活动对内蒙古托克县浅层地下水中的硝酸盐的驱动作用,结果显示人类污水灌溉、粪便堆放、化肥施用对该区域地下水中的硝酸盐具有很高的贡献率;郇环[8]等人利用普通克里金插值方法对松花江吉林段沿岸浅层地下水中硝酸盐的氮浓度分布特征作了分析,结果显示常数趋势球型模型适用于描述研究区地下水NO3-N浓度分布空间变异性,NO3-N浓度在一定范围内存在空间相关性,空间相关距离为相对较大,前人对浅层地下水中的污染因子研究较多的是其污染来源、空间分布变化及水质评价。本篇论文是采用地下水数值模拟软件对研究区中的氨氮在现状污染的基础上,预测其未来的污染变化趋势,对保护地下水资源具有一定的指导意义,数值模拟方法灵活,适用于各种复杂的水文地质条件,在处理地下水流、地下水溶质运移和水资源环境分析等方面有良好的效果[9-11]。

本文以云南保山盆地地下水污染为例,借助水文地质相关资料,结合研究区的实际核心特征,利用GMS专业软件对污染物进行仿真模拟,建立研究区内流场的数学研究模型,选用氨氮作为特征因子,预测特征因子的运移规律对地下水造成的环境影响。数值模拟对地下水开采、治理、环境问题和资源的评价开发等提供参考意义[12-13]。

经研究,该区域氨氮污染的主要来源是保山地区动物的禽畜粪便的排放,经相关资料统计出该区域的动物的数量,折合成标准猪,每年每头猪的粪尿排放量为1.2 t,粪尿中的2%排入到土壤中,经降雨入渗排的氨氮含量每年是25.01 t;农业过度施肥也是造成地下水中氨氮超标的主要来源,保山的第一产业是农业,大面积农作物需要施肥,导致土壤中含有大量的含氮化肥,经计算,保山每年经降雨淋滤进入地下水中的总氮为212.4 t;工业污水的排放与泄露,经调查研究,研究区内共有92座工业企业的废水直接排入到东河内,每年排放污水的总氮含量是29.28 t。若不及时治理,地下水中的氨氮会在特定环境下转化为亚硝酸盐,亚硝酸盐含量的升高会增加人体患癌症的几率;当然地下水中的氨氮超标对生态环境也有极大的危害,会造成鱼类的死亡,破坏生态平衡。

2 研究区概况与污染现状

2.1 概况

以云南保山盆地为研究区,其区域内水文地质条件稍显复杂,地下水类型划分较多,盆地内的第四系松散层孔隙水与地貌类型密不可分,因此该区内的孔隙水在外在形式上表现出多种多样,冲洪积扇孔隙水具有较强的富水性,主要以鹅卵石为主,钻孔单位涌水量很大;冲湖积平原孔隙水因地势较为平坦,地下水位埋深较浅,等水位线走势常年保持基本不变;冲洪积平原孔隙水,富水性中等,盆地内的地下水具有各项异性的特征。本次重点研究的工作是第四系松散层内的孔隙水的污染核心特征,该地下水类型主要接受大气降雨的自然补给,还有部分接受周围具有水力联系的基岩裂隙水的径流补给,最终均以泉的形式以及下游向侵蚀基准面较低的东河排泄。研究区内的地下水取样点见图1。

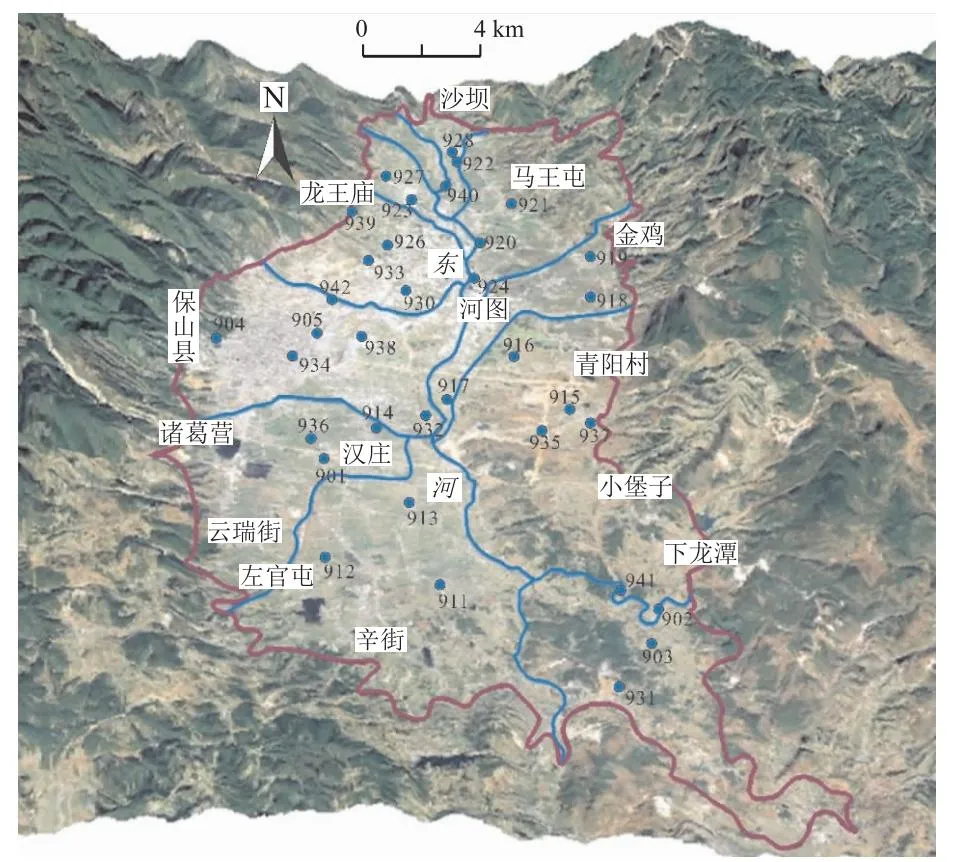
图1 研究区地下水取样点图

2.2 污染现状

根据2019年采取盆地内35个浅层地下水样品的检测结果显示,氨氮的浓度在0.02～17.9 mg/l,取样点中汉庄镇914处、盆地东侧青阳村916处、板桥镇920处及河图镇924处的氨氮浓度高于地下水Ⅲ类标准(<0.5 mg/ l),且最高浓度在916处,研究区内的氨氮主要集中在东河区域附近,越靠近东河,污染越严重,由此可见工业废水的排放对东河附近的地下水污染是最严重的,若不及时处理,东河附近的居民较多,不知情的情况下,饮用氨氮超标的地表水和地下水,均会影响居民的身体健康。氨氮的污染现状图见图2。由氨氮的污染现状图显示,盆地内孔隙水中的氨氮污染区域较大,主要集中在盆地的上游,下游盆地内地下水中的氨氮并未污染。

图2 氨氮污染现状图

3 水文地质特征及概念模型

3.1 研究区区域地质条件

水文地质概念模型可以很好地反应研究区内地下水的流向,可以将复杂的问题简单化,在计算机上清晰地反应出来。

研究区的水文地质条件较为复杂,盆地内主要是第四系覆盖层,该层主要是富水性较强的孔隙水含水层组,该层地下水因地貌类型不同,主要有第四系冲洪积扇孔隙水,冲湖积平原孔隙水,冲洪积平原孔隙水,孔隙水中的隔水层主要是上部粘土层,而含水层主要是下部的带有卵砾石的泥砂层。主要分布在盆地内及盆地边缘与岩层的交界处。

裂隙水含水层主要分布在盆地西部和东部的基岩中,因基岩区中的裂隙发育多,地下水赋存于此,主要的含水层是粉砂岩,而主要的隔水层则是板岩。

岩溶水含水层主要是研究区内碳酸盐岩夹碎屑岩裂隙溶洞水,主要分布在东侧及盆地下游侧,研究区内的水文地质图见图3。从研究区的剖面图可以看出地下水含水层的补给关系,盆地内的第四系孔隙水,主要接受碎屑岩裂隙水及碳酸盐岩岩溶水的补给,见图4。

图3 研究区水文地质图

图4 研究区水文地质剖面图

3.2 研究区概念模型

因本篇论文主要研究的第四系孔隙水,研究区内地下水流场模型的范围是第四系含水层,地层中的黏土层是主要的隔水层,而主要的含水层是卵砾石层。盆地中的卵砾石层与碳酸盐岩相交的部分,接受基岩裂隙水的补给,因而可以看作是向研究区内松散孔隙水的定流量边界的界限,而基岩覆盖层中的黏土与红黏土,因透水性差,故而可以看作是隔水边界。而主要的含水层的补给途径主要是大气降水以及基岩的横向补给,最终向低洼地区的东河流域排泄,该流域的整体流向贯穿整个盆地的南北向,由地下水与地表水的水力联系可看出,该河流可作为定水头边界。依据上述假设的边界条件的界限以及该区域内的水文地质特征,建立研究区的水文地质概念模型见图5所示。

图5 研究区水文地质概念模型图

3.3 数学模型

对于新建的地下水流场模型使用偏微分方程数值化。因研究区内的地下水是承压含水层,且具有非均质各项异性的特性,故使用以下的微分方程来求解:

(1)

其中,Kxx,Kyy,Kzz为各主方向上的渗透系数,m/d;H为承压含水层水头,m;Ss为储水率,单位m-1;W为源汇项,m3;t为时间,单位d。

求解该方程需要的初始条件为零时刻的边界条件。

H(x,y,z,t)Si=φi(x,y,z,t)(x,y,z)∈Si

(2)

因地下水流场中的偏微分方程具有较多的未知数,也缺少很多条件,因此很难解得具体的解析解,为了解决这一难题,引进数值模拟的办法来求得上述微分方程的近似解。

数值模拟过程主要是利用有限差分的方式将模拟的区域划分为若干的小网格,研究每个小网格中的流场特征,最终以替代的思想将研究区的整体流场特征用每个小网格的模拟水位来代替,进而实现离散的目的,将不能求解的复杂微分方程转化为可求解的简单数学问题,忽略微小的误差。

3.4 数值模型建立

3.4.1 建立模型

根据该区的岩性特征分析,以卵砾石含水层为主要的研究对象,含水层上下部的黏土可概括为隔水层,也就是对应的储水界面,按模型面积划分成200 200×400×3的网状结构。利用以上假定的边界条件,将研究区内的水文地质概念模型转化为数值研究模型,参见附图6.

图6 研究区数学模型三维地质网格图

3.4.2 源汇项

(1) 补给项

该区的卵砾石含水层是由大气降水和基岩裂隙水横向供给的。根据相关的水文气象数据,得出了以卵砾岩为基础的降雨入渗系数为0.24的降水量,并据此推算出了降水对地下水的补充量为0.000 692 3 m/d。

而四周基岩裂隙水的补给量可根据达西公式计算:

Q=KAJ

(3)

式中,Q为周围基岩区侧向径流孔隙水的补给量,m3;K为渗透系数,m/d;J为水力梯度;A为过水断面的面积,m2。

由研究区内岩性出露的条件及地下水位的关系看出,与该区内的孔隙水具有水力联系的基岩裂隙水主要是西部胡家坝、庄家坡、龙王庙,北部沙坝及东部青阳村、大关庙等地。据此计算出了侧向补给总量为2 096.83 m3/d。

(2) 排泄项

因主要的含水层是承压水且上覆土层具有隔水性质,故模型中不考虑蒸发排泄。研究区的孔隙水主要通过周围地势较低的河流、泉及少量的民井排泄。

(3) 水文地质参数

渗透系数是反应岩土渗透性的重要指标,也是建立流场模型及溶质运移模型必备的参数,因研究区内出露的岩性较多较复杂,因此按照钻孔抽水试验、地层岩性及地形地貌等因素划分渗透系数分区,盆地内的第四系覆盖层厚度变化较大,展现出中间厚、边缘薄的特点,且沿着冲积扇,卵砾石层与粘土层交替沉积,且厚度不一,因此盆地内不同区域的渗透系数存在差异,呈现为非均质性。本次将研究区孔隙水含水层划分为27个子区域,在建立模型时,对不同的区域进行赋值,以达到模型的准确性,其参数分区平面图见图7,分区表见表1。

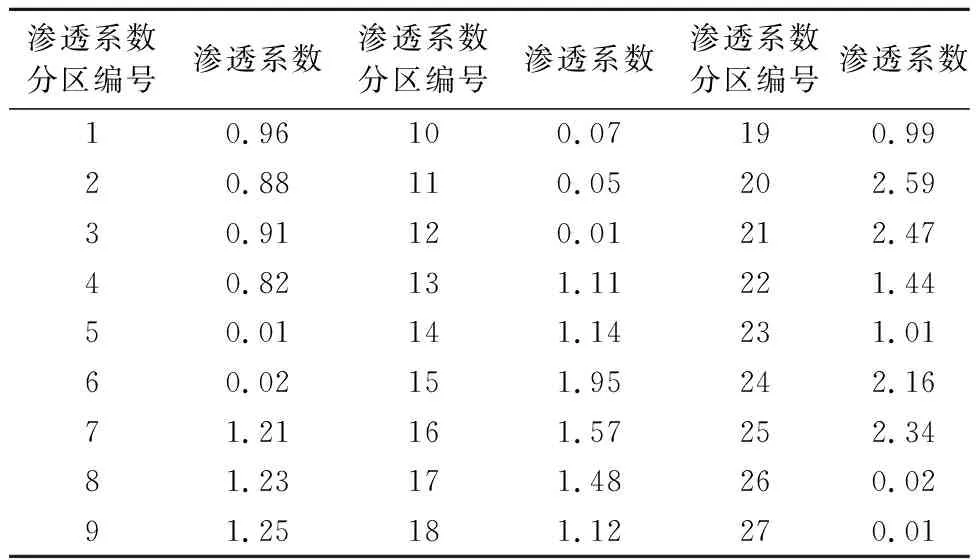
表1 渗透系数分区表

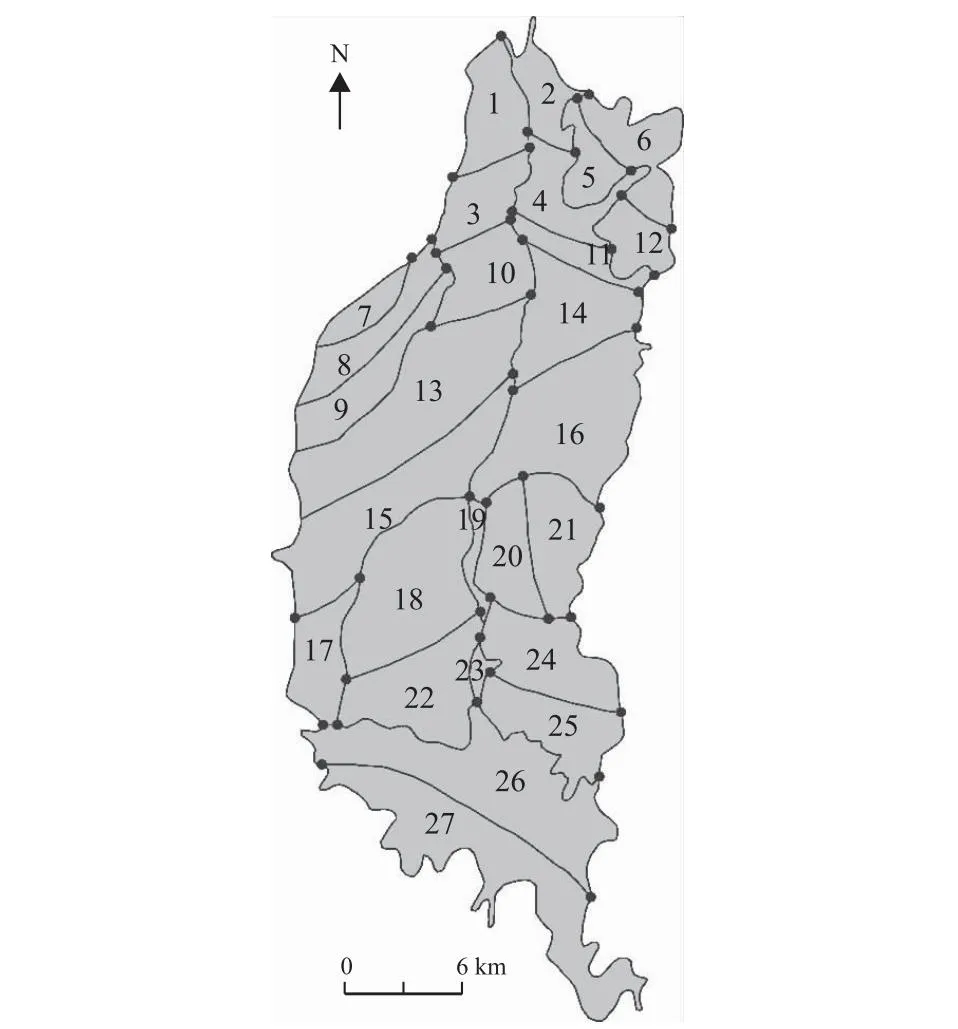
图7 渗透系数分区图

根据保山的地质勘察资料及实际工程经验,研究区的平均孔隙度设定为0.28。

(4) 弥散度

根据研究区做的弥散试验,结合研究区的研究面积,本次模拟的孔隙水含水层纵向弥散度为0.82 m,横向弥散度为0.19 m。

4 地下水溶质运移模型

4.1 模型建立

对于利用GMS建立污染物的溶质运移模型,诸多学者也有许多研究,刘娟等[14]对某市岩溶地下水污染进行研究,运用FEFLOW 软件对拟建好的数学研究模型求解,探究研究区内流场的特征,在水流模型的基础上进行溶质运移模拟,模拟了地下水中四氯化碳污染羽的浓度场,并预测了未来浓度场的变化;于翠翠[15]运用地下水模拟软件 GMS 对山东济南明水泉域地下水流场进行了数值模拟,对泉域岩溶地下水资源总量和地下水可采量进行了评价,并对泉水动态水位进行预测;颜萍[16]利用GMS对保山某尾矿库的地下水污染物进行污染预测,针对得到的预测结果,提出治理污染的措施。

该地区内的氨氮的污染来源主要是禽畜粪便、农业过度使用含氮化肥以及工业污水的随意排放造成的,上述污染源通过上部地层的孔隙经降雨淋滤进入到研究区内的含水层中,最终沿地下水流向方向迁移。本次工作研究的重点是仅考虑地下水的对流及弥散作用运用GMS专业模拟软件中的MT3D模块结合上述建立的流场数值模型建立研究区内的溶质运移模型,探究预测特征因子在1 000 d、3 000 d、5 000 d后氨氮的地理位置以及中心浓度的运移方向。根据水动力弥散理论,研究区内地下水溶质运移控制方程如下:

(4)

式中,C为地下水中污染物浓度,mg/l;n为孔隙度;Dij为水动力弥散系数,m;vi为地下水渗流速度,m/d;qs为源汇到含水层内单位体积的流量;Cs为源汇项中污染物浓度;Rn为化学反应项。

初始条件和边界条件为:

C(x,y,z,t)|t=0=C0(x,y,z)∈Ω

(5)

C(x,y,z,t)|Γ1=CI(x,y,z) (x,y,z)∈Γ1∈Ω

(6)

式中,C0为地下水污染物初始浓度,mg/l;Ω为模拟区域;CI为边界污染物浓度,mg/l;Γ1为浓度边界。

因条件限制,该模型中仅考虑了地下水的对流作用及弥散作用,故模型不考虑污染物的质量衰减的因素。利用GMS软件模拟预测研究区内氨氮的运移规律。

4.2 模拟预测及结论

根据研究区采集到的地下水中氨氮浓度的检测结果,利用克里金插值方进行插值计算,可知氨氮在研究区内的现状污染情况,以及现状条件下氨氮的实际迁移距离见图8。结合研究区内氨氮的污染原因,依据数据资料分析可计算出每天地下水中有0.001 35 mg/l的氨氮进入,这里将氨氮的单天渗入量作为模拟的初始源强,模拟预测氨氮在1 000 d、3 000 d、5 000 d后高浓度地区的位置、浓度变化以及迁移距离,参见附图9(a、b、c)。

图8 氨氮污染现状及实际迁移距离图

图9(b) 氨氮迁移 3 000 d浓度变化及理论距离图

图9(c) 氨氮迁移5 000 d浓度变化及理论距离图

由上述模拟预测图表明,仅考虑对流及弥散作用时,模拟的3个时间段内氨氮的理论迁移距离与实际迁移距离相比有明显的变化。以上述计算出单日氨氮进入地下水的含量作为源强,对比氨氮现状污染的迁移距离,1 000 d后,东侧部分的的氨氮向盆地中心处的东河运移了14.9 m,而西侧向盆地中心处的东河运移25.7 m;3 000 d后,东侧部分的氨氮向东河运移了49.7 m,西侧向东河运移80.5 m;5 000 d后,东侧部分的氨氮向东河运移了85.7 m,西侧向东河运移了136.3 m。由此可以看出模拟预测的3个时间段内,氨氮两侧的浓度均向盆地中心的东河移动,并且理论迁移的距离与时间呈现正相关性。由前述可知,东河是盆地内的低洼地区,研究区内地下水最终排泄到东河内,根据模拟结果也可以看出(表2),氨氮都是沿着地下水流方向迁移的,并且时间越长,最高浓度在缓慢变小。利用氨氮实际运移距离与理论运移距离的比值可以看出,西侧的比值比东侧的大,说明西侧的氨氮更易沿水流方向向东河迁移。