罗平县崩滑易发性评价模型对比研究

杨得虎,朱杰勇,刘帅,马博, 代旭升

(1.昆明理工大学国土资源工程学院,昆明 650093;2.云南省地质环境监测院,昆明 650216)

崩滑地质灾害的广泛发育威胁着人们的生命财产安全,其灾害的发生受自然因素和诱发因素影响[1]。

随着地理信息系统(GIS)的不断发展,基于GIS技术的地质灾害易发性评价已成为评估的有效工具和研究领域的热点[2]。本文选取罗平县作为研究区建立崩滑易发评估模型,对今后城市的发展和防灾减灾有重要意义[3],也可为岩溶地区地质灾害易发性评价提供一定的依据。

目前,地质灾害易发性评价主要为定性、定量两种评价方法[4]。随着技术的不断发展,机器评价方法也逐渐得到普遍运用。定性分析是通过对成因机制的全面认识,基于专家经验和知识确定评价因子权重,定量分析方法通过数学或数值算法估计滑坡易感性[5]。定性分析方法主要有层次分析法[6-8],定量分析方法主要有频率比法[9,10]、信息量法[11,12],机器学习方法有logistic回归法、随机森林法、K近邻、支持向量机和神经网络等[13-15]。通过对国内外学者研究进行分析,单一模型的评价结果精度较低,现多采用耦合模型和机器学习方法进行评价。吉日伍呷等[15]通过logistic回归、K近邻、朴素贝叶斯和 随机森林算法对鲁甸地震进行地震滑坡易发性评价;樊芷吟等[16]通过信息量模型和Logistic回归耦合模型对汶川县地灾进行易发性评价;张晓东[17]通过层次分析法、支持向量机和地理加权回归等模型对宁夏盐池县地灾进行易发性评价。从以上研究可以发现,单一评价模型在因子分类级计算时主观因素较大,其评价结果存在一定的缺陷,现采用多种耦合模型和机器模型对地质灾害进行评价成为新的探索方法。基于耦合模型和机器模型的评价方法可以降低主观性因素的影响,解决评价因子之间的数据整合问题,使评价结果更加精确和可靠。

本文以罗平县作为研究区域,根据崩滑地质灾害的形成条件选取基础地质、地形地貌、地质构造、水文环境和外界触发等5类评价指标。采用定量评价方法信息量法和频率比法计算评价因子分类分级权重,再选取逻辑回归法对评价因子进行权重计算,以此构建信息量模型(ICM)、频率比模型(NFR)和以及与逻辑回归(LR)耦合的信息量-逻辑回归(ICM-LR)耦合模型和归一化频率比-逻辑回归(NFR-LR)耦合模型对罗平县崩滑地质灾害进行易发性评价,并对评价结果进行精度检验分析,得出精度最高的评价模型,可为快速建立评价指标体系和区域崩滑地质灾害监测预警系统及防灾减灾提供参考。

1 崩滑易发性评价模型

1.1 信息量模型(ICM)

信息量模型(information content method, ICM)是将崩滑历史数据进行统计分析,将影响崩滑的因子分类级得实测值转化为信息量值,来衡量崩滑的易发性[18]。首先计算所选评价因子分类级的信息量值,再对各因子信息量值进行总和,作为崩滑易发性的综合指标[19]。单因子信息量计算公式:

(1)

式中,I为评价因子j下的信息量;Nj为评价因子j内发生的崩滑数;N为研究区崩滑总数;Sj为评价因子j下所占栅格数;S为研究区栅格总数。

根据选取的评价因子进行分类级计算,各因子分类级的信息量值决定地质灾害发生的可能性,将各分类级因子叠加计算的总信息量计算公式为:

(2)

式中,Ij为总信息量,为崩滑地质灾害易发性指数;Ij值越大且为正值则表示该单元内有利于崩滑发生。

1.2 归一化频率比模型(NFR)

频率比模型(frequency ratio,FR)是将崩滑点分布情况与评价因子分类级的空间关系进行分析。推导出崩滑发生概率与评价因子之间的关系,从而反应出各分类级对崩滑发生的影响程度,FR值越大则表示对崩滑发育的贡献越大[20]。其频率比计算公式如下:

(3)

式中,FR(xij)为频率比值;zij为第i个评价因子j类发生崩滑的个数;Z为研究区内崩滑的总数;sij为第i个评价因子j类区间的面积;S为研究区总面积。

归一化频率比模型(normalized frequency ratio,NFR)是将各频率比值做归一化处理,其公式如下:

(4)

式中,NFR(Xij)为归一化频率比值。

1.3 逻辑回归模型(LR)

逻辑回归模型(logistic regression,LR)是一种研究二分类因变量常用的统计方法[21]。通过研究崩滑易发性与评价因子之间的关系,预测崩滑发生的概率。其中自变量为评价因子指标值(x1,x2,…,xn),是否发生地质灾害作为因变量(1和0分别代表崩滑点和非崩滑点)。Logistic回归函数如下:

Z=α+β1x1+β2x2+…+βnxn

(5)

(6)

式中,α为常数项;x1,x2,…,xn为自变量;β1,β2,…,βn为回归系数;Z为崩滑发生的可能性与各评价因子之间的关系;P为崩滑灾害发生的概率,范围0～1。

1.4 耦合模型

将ICM模型和NFR模型分别与LR模型进行耦合,可解决单一模型因子分类级的数据整合问题和降低人为主观性因素影响问题。首先对所选因子进行共线性诊断分析,保证评价因子的独立性。将ICM模型和NFR模型计算得出的各评价因子分类级的值作为LR模型的自变量,建立回归方程,得出各评价因子的回归系数,再计算评价单元的崩滑概率,以此为依据分别建立ICM-LR 模型和NFR-LR 模型对研究区进行崩滑易发性评价。

2 研究区概况及数据来源

2.1 研究区概况

研究区(罗平县)位于云南省曲靖市东部。地理坐标为24°31′～25°25′ N, 103°57′～104°43′ E,东西最大横距75 km,南北最大纵距99 km,全县国土面积3 018 km2(图1)。研究区西部和北部属于岩溶盆地地貌和岩溶低中山地貌,中部属岩溶断陷湖形盆地,东部和南部受九龙河和南盘江流域侵蚀切割,形成峰林洼地和岩溶中山地貌。区内地层出露主要有古生界泥盆系(D)浅灰、深灰色中厚层状灰岩、泥灰岩、泥质白云岩;石炭系(C)深灰、灰黑色块状灰岩、白云质灰岩、泥质灰岩;古生界二叠系(P)灰、深灰色厚层块状、生物碎屑灰岩,结晶灰岩夹虎斑状灰岩及白云岩;中生界三叠系(T)上统为黄褐色粉砂岩、泥质粉砂岩及细砂岩,中统为深灰色灰岩夹泥质灰岩,中上部为黄色白云岩,下统为紫红色含长石粉细砂夹泥灰岩页岩及含铜页岩;新生界第三系(N)褐黄紫红色砾岩、细砂岩及粉砂质泥岩,底部砾岩;新生界第四系(Q)细砂、砂砾石及砂质粘土。区内位于云南山字形构造的东翼。主要构造体系和构造型式有北东向构造、新华夏系构造、网状构造等。主要断裂有:金鸡山断裂、长家湾断裂和腊庄断裂等。其次为新华夏系构造,多发育在褶皱边缘,密集成束,规模大、延伸远,呈舒缓波状,主要分布在西部及南盘江两岸。主要断裂有:洒土革断裂、大水塘断裂、罗格断裂等。

图1 罗平县崩滑分布图

2.2 数据来源

本研究数据主要包括:(1)12.5 m分辨率数字高程模型(DEM),用于提取坡度、坡向、起伏度、曲率等评价因子;(2)1∶5万地质图,用于提取岩性、断裂等因子;(3)1∶5万全国基础地理数据库,用于提取水系、道路等评价因子;(4)历史崩滑数据:主要来自1∶5万全区调查和1∶1万重点区罗平县地质灾害详细调查资料以及野外补充资料;(5)地质灾害点的基础数据来自于地矿眉山工程勘察院的详细调查结果,共包含154个崩滑灾害点的数据,滑坡136处,崩塌18处。

3 评价因子分析

本文在研究区资料收集和野外调查的基础上,选取基础地质(工程岩组、断层缓冲距)、地形地貌(坡度、坡向、高程、起伏度、曲率、地貌类型)、水文环境(河流缓冲距)、外界触发(降雨量)等5大类中的10个评价因子进行分析。根据12.5 m×12.5 m栅格单元作为易发性评价的制图单元,通过对研究区评价因子进行归纳分析,将崩滑灾害点与各评价因子进行空间关联分析,通过重分类得到各崩滑点在各评价因子的分布情况。对各评价因子的分类级处理如图2和表1所示。

3.1 基础地质因子

选取工程地质岩组、断裂缓冲距作为崩滑易发性评价的地质类因子。工程地质岩组是崩滑发育形成的重要内因,不同岩组的力学参数存在较大差异,从而影响坡体的稳定性[22]。区域内崩滑点主要分布在层状结构坚硬长石石英砂岩岩组,中厚层状坚硬灰岩、白云岩岩组,其FR值大于1,在层状结构坚硬长石石英砂岩岩组中崩滑点分布相对密集。地质构造中的断裂多发育在褶皱边缘,且密集度、规模大、延伸远,对两侧岩层强烈挤压扭曲牵引,对地质灾害的发育起控制作用。将研究区断裂按600 m等距离分为6类缓冲区,断裂缓冲距小于600 m以内时,FR值大于1,表明区域内距断裂越近,越有利崩滑地质灾害的发生。

图2 评价因子分类级图

表1 评价因子分类级计算表

3.2 地形地貌因子

地形地貌因子是滑坡发育敏感性程度的重要因素[23]。研究区地形地貌因子均从12.5 m×12.5 m分辨率的DEM中提取,分别提取了高程、坡度、坡向、曲率、起伏度等评价因子。将研究区高程分成8个区间,崩滑点主要分布在715～860 m、1 200～1 350 m、1 650～1 800 m区间内,其FR值均大于1,其最高值为1.44。坡度和坡向的组合与土层厚度、土壤湿度、光照强度存在密切关系[24],将研究区坡度和坡向分成8个区间,崩滑主要分布在坡度6°～24°之间,坡向朝东、东南、南、西北时,FR值均大于1。表明该区间内有利于崩滑的发生。地形起伏度反映地形的起伏情况,地形起伏度较大的地区为崩滑灾害的发生提供了物质条件和地形条件[25]。将起伏度因子分为8个区间,起伏度为8～15 m、30～38 m易发生,FR 值分别为1.53、2.80。地形曲率在微观尺度上反映了地表形态[26]。曲率的数值可以反映斜坡的形态,将其分为3个区间,值小于0代表凹形坡,值为0为平形坡,值大于0为凸形坡。其中凹形坡的FR值更大,说明其比其它两种坡形更易发生崩滑地质灾害。

3.3 水文环境因子

地表水系的侵蚀和切割为滑坡灾害提供了重要的诱因[27]。将区域内河流按600 m等距离分为6类缓冲区,河流缓冲距1 800 m以内时,FR 值均大于1,当河流缓冲距在600 m以内时,FR值为1.96。表明区域内距河流越近越有利于崩滑灾害的发生。

3.4 外界触发因子

地形地貌、地质构造、工程岩组等是地质灾害形成的主要控制因素,降雨作为诱发因素,其强度大小与地质灾害的发生密切相关。将研究区降雨量值分为6个区间,当降雨量值大于1 300 mm时,崩滑灾害分布较多,其值为1 300～1 400 mm时FR值为1.16。

4 罗平县崩滑易发性评价

4.1 评价因子信息量值和频率比值的计算

根据研究区已有的154个崩滑点,通过对各因子进行分级并统计灾点比和面积比,利用公式(1)和(3)计算得到各因子分级区间的信息量值和频率比值,根据不同方法计算得出的结果,从而分析不同因子区间的重要性。各因子分类级的信息量值和频率比值如图2和表1所示。

4.2 评价因子共线性诊断

崩滑地质灾害易发性评价指标体系中,需要保证自变量相互独立,相关性高会出现多重共线性[21],将影响模型的准确性。因此采用容忍度(Tolerance, TOL)和方差膨胀因子(Variance Inflation Factor, VIF)对自变量进行多重共线性诊断:

(7)

其中,R2是以xi为因变量时对其他自变量回归的复测定系数。TOL为VIF的倒数,当TOL>0.1且VIF<10时,说明自变量不存在多重共线性。通过SPSS软件进行多重共线性诊断,结果如表2所示。结果显示对所选10个评价因子其VIF值在1～1.5。其VIF<5,表明各因子之间相互独立,不存在共线性。

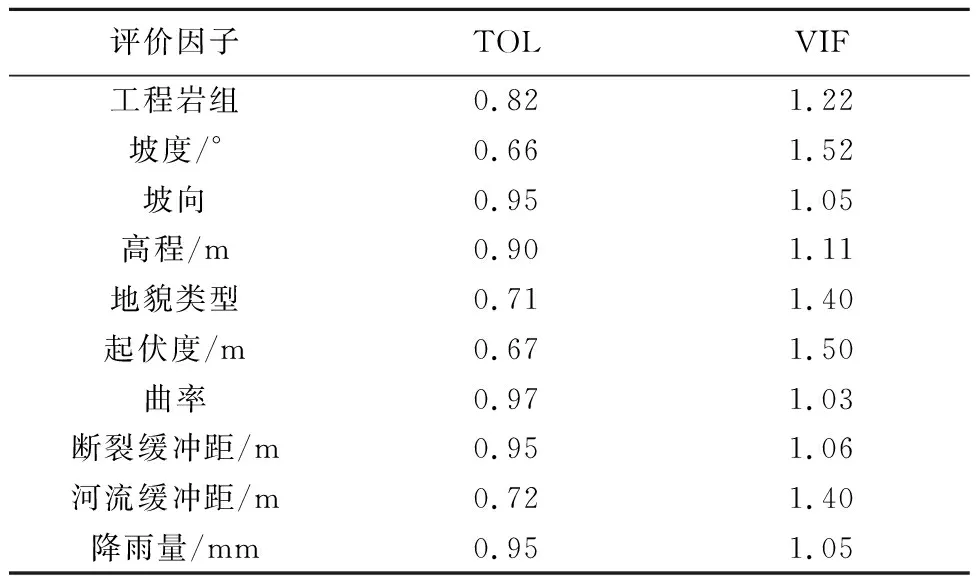
表2 评价因子VIF计算结果表

4.3 评价因子相关性分析

崩滑的易发性与评价因子之间存在一定的相关性。为了保证各评价因子间的相互独立性和结果的可靠性,进行因子相关性检验[28],结果如表3所示。结果显示各评价因子之间的相关系数均<0.3,评价因子之间的相关性较小,所以10个评价因子均可以进入模型。

4.4 评价因子逻辑回归分析

根据研究区已有的154个崩滑点,并随机选取等量的非崩滑点,共计有308个独立属性的统计样本。提取每个样本的各类级信息量值和频率比值作为自变量,是否发生地质灾害作为因变量(1和0分别代表崩滑点和非崩滑点)。分别导入SPSS软件中进行二项逻辑回归运算,当选取的评价因子显著性均≤0.05时具有统计意义[21]。在I-IR模型中,曲率的显著性为0.54,计算时应剔除。NFR-IR模型中,坡向和曲率的显著性为0.36和0.25,计算时剔除,其余评价因子的显著性均<0.05。其I-LR和NFR-LR的回归运算公式为:

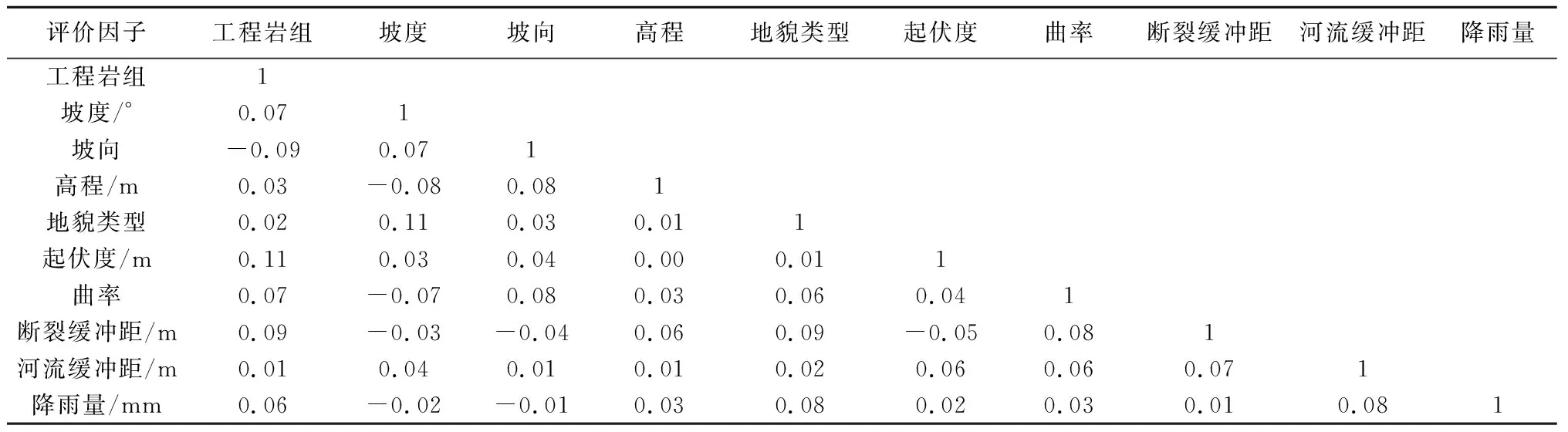
表3 评价因子之间的相关系数矩阵

(8)

(9)

式中,x1～x10分别为工程岩组、坡度、坡向、高程、地貌类型、起伏度、曲率、断裂缓冲距、河流缓冲距、降雨量的ICM值和NFR值。

5 崩滑易发性评价结果与精度评价

5.1 单一模型评价结果

根据表1所求出各评价因子分类级的NFR值和ICM值,进行叠加分析,分别得到罗平县崩滑地质灾害的易发性分布图,利用ARCGIS的自然断点法将其分为极高、高、中、低4个区间。结果如图3(a～b)和表4所示。其中ICM模型中,低-极高易发区的面积(频率比)分别为529.96 km2(0.33)、943.72 km2(0.46)、979.64 km2(0.96)、564.67 km2(2.60)。在极高易发区内,崩滑点占总灾点的48.7%。NFR模型中,低-极高易发区的面积(频率比)分别为562.54 km2(0.28)、908.48 km2(0.8)、950.81 km2(1.13) 、596.17 km2(1.97)。在极高易发区内,崩滑点占总灾点的38.96%。两种单一评价模型中,从低-极高易发区崩滑易发性的频率比逐渐增大。且低-中易发区间内,频率比值都小于1,说明两种单一模型均可以有效对罗平县崩滑易发性进行评价。

5.2 耦合模型评价结果

利用GIS的栅格计算器功能,将ICM-LR耦合模型和NFR-LR耦合模型按照公式(8～9)进行逻辑回归分析计算,得到相应评价模型的崩滑易发性分布图,利用ARCGIS的自然断点法将其分为极高、高、中、低4个区间。结果如图3(c～d)和表4所示。在ICM-LR耦合模型中,低-极高易发区的面积(频率比)分别为771.1 km2(0.25)、836.6 km2(0.73)、864.36 km2(0.88)、545.94 km2(2.66)。在极高易发区内,崩滑点占总灾点的48.05%。NFR-LR模型中,低-极高易发区的面积(频率比)分别为548.52 km2(0.25)、940.12 km2(0.71)、989.08 km2(0.95)、540.28 km2(2.36)。在极高易发区内,崩滑点占总灾点的42.21%。两种耦合模型评价结果比较一致,从低-极高易发区崩滑易发性的频率比逐渐增大。且低-中易发区间内,频率比值都小于1,ICM-LR耦合模型低易发区的面积较单一模型相对增大,且两种耦合模型各分区面积相对一致,说明耦合模型更能准确对罗平县崩滑易发性进行评价。

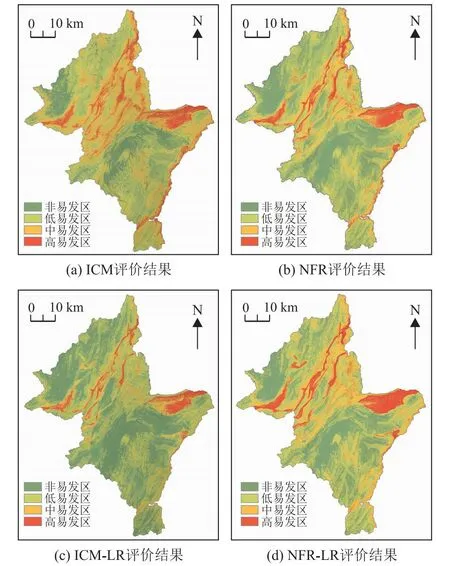
图3 罗平县崩滑易发性评价结果

表4 罗平县崩滑易发性评价频率比

5.3 评价精度对比分析

本文采用ROC(receiver operating characteristic)曲线对ICM模型、NFR模型、ICM-LR耦合模型和NFR-LR耦合模型的易发性评价结果进行精度检验。ROC曲线又称接收者工作特征曲线,其横轴为假阳性率(1-特异性),纵轴为真阳性率(敏感度),根据其线下的面积大小作为评价方法准确性评价的指标。ROC曲线的线下面积用AUC值来表示,值越大,实验的准确率越高,模型的预测效果越好[29]。4种评价模型ROC曲线如图4所示。AUC值分别为0.820、0.796、0.882及0.840,耦合模型的精度较单一模型的精度高,其中ICM-LR耦合模型的精度最高,该模型更能准确对罗平县崩滑地质灾害易发性评价研究。

图4 ROC曲线

6 结论

(1) 以罗平县为研究对象,选取工程岩组、坡度、坡向、高程、地貌类型、起伏度、曲率、断裂缓冲距、河流缓冲距、降雨量等10个评价因子,对因子进行独立性检验,选取信息量模型(ICM)、频率比模型(NFR)以及与逻辑回归(LR)耦合模型对罗平县崩滑地质灾害进行易发性评价。

(2) 通过对评价因子的分类级处理,计算信息量值和频率比值,通过信息量正值和频率比值得出影响较大的因子类级分别是:工程岩组中的层状结构坚硬长石石英砂岩岩组、地貌类型中的岩溶中山地貌和侵蚀谷地地貌、坡度主要分布在6°～30°度之间、高程集中在1 350～1 950 m之间、起伏度在23 m以下、断裂缓冲距和河流缓冲距1 800 m之内、降雨量集中在1 300～1 600 mm之间,对崩滑发育具有促进作用。

(3) 根据构建的ICM、NFR、ICM-LR和NFR-LR模型进行对比研究,通过ROC曲线对4种模型的精度进行检验,AUC值分别为0.820、0.796、0.882和0.840,耦合模型的精度较单一模型的精度高,其中ICM-LR耦合模型的精度最高,表明该模型更能准确对罗平县崩滑地质灾害易发性评价研究。

(4) 基于ICM-LR耦合模型的评价结果得出,极高易发区主要分布在砂岩、碳酸盐岩组区域和水系延展区域。