如何“以不变应万变”

王秋叶

摘要：“动点问题”不仅可以考查学生对所学知识的掌握程度，也能体现学生的数学逻辑思维水平及直观想象能力.综观初中各类试题，多将“动点问题”列为压轴题，发挥其选拔功能.从教学现状来看，多数学生面对“动点问题”时无法确立“动点”与“静点”之间的关联，无法正确解答这类问题.基于此，文章结合具体实例，对初中数学“动点问题”单元的课前教学设计进行探究.

关键词：初中数学；动点问题；教学设计

中图分类号：G632文献标识码：A文章编号：1008-0333（2023）32-0008-03

“动点问题”教学是初中平面几何教学中的一个难点[1].“动点问题”大多需要结合几何、函数等方面的数学知识解决，而这些内容本身就是初中数学教学的难点，再加上动点的“不确定性”，学生难以准确判断各数量间的关系，因而此类问题的正确率一直都不尽如人意.为提高学生的综合解题能力，教师在设计“动点问题”单元教学时，应立足学生核心素养的培育，引导学生建立“动点”与“静点”间的有效关联，“以不变应万变”顺利解决此类问题.

1 数学动点问题的含义和例举

1.1 数学动点问题的含义

所谓“动点问题”是指图形中存在一个或者多个动点，它们在线段、射线或弧线上运动的一类开放性题目[2].这一类题目看起来有很多不确定性，随着点的位置的变化，题设中的一些变量也会随之改变.而解决这类问题的关键就是在运动变化中找出不变的数量关系和位置关系，“以不变应万变”是解决此类问题的关键.在解决此类问题时，需要用到方程思想、转化思想、分类思想、数形结合思想等数学思想，其综合性较强，有一定的难度.

1.2 单元数学动点问题的例举

研究近年来连云港市的中考试题，就能大致了解到当年连云港市中考数学试题的考查热点和试题的命题方向，它能帮助各年级的数學教师在教学中注意研究解决问题的方法和策略，为平时的教育教学工作指明方向.只有如此，一线教师才能在平时的教学中更好地培养学生解题素养，更明确地体现新课程标准的导向.本文拟就压轴题的题型背景和解题思路具体阐述自己的观点.

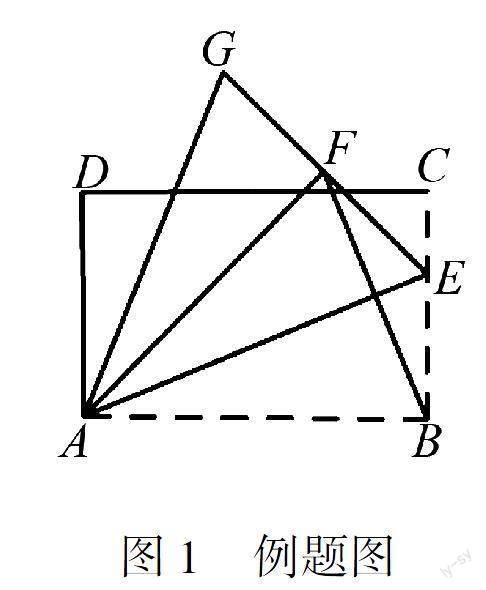
例题如图1，在矩形ABCD中，AD=23AB=4，点E是线段BC上的一个动点，连接AE，将△ABE沿着AE翻折得到△AEF，其中点G是∠DAF的平分线与EF延长线的交点，若点E从点B运动到点C，则点G运动的路径长为.

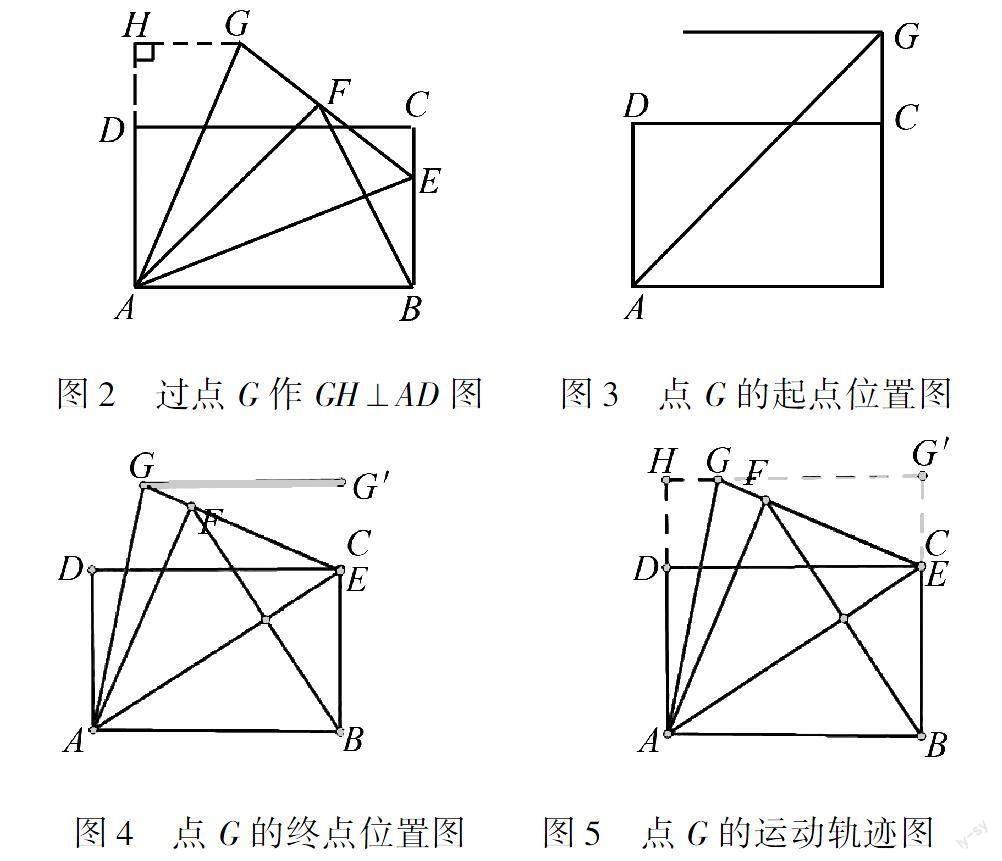
分析本题是以矩形为基础图形，在边BC上有一个动点E（变），连接AE，将△ABE沿着AE折叠得到△AEF.此时涉及图形运动——翻折.根据翻折的性质，容易得到AF=AB=6，EF=EB，∠FAE=∠BAE.而AG是∠DAF的平分线，过点G作GH⊥AD，交AD的延长线于点H，如图2所示，易证△AGH≌△AGF.因此，无论点E在哪里，总有GH⊥AD，且AH=AF=AB=6（不变）.点G在经过点H且平行于CD的直线上运动，即点G的运动轨迹为线段GH.当点E与B重合时，确定G的起点，如图3所示；当点E与C重合时，确定点G的终点，如图4所示.

点G的轨迹是线段GG′，如图5所示.

设GH=x，那么GG′=6-x，GF=x，CG=4+x.易证G′H=AB=6，DH=CG′=2.在Rt△GG′C中，由勾股定理得CG′2+GG′2=GC2，即22+（6－x）2=（4+x）2.求得x=1.2，GG′=6-x=4.8.

由此可以看出，具体解题步骤为：求出AB=6；确定点G的运动路径，即线段GG′；当点E与B重合时，确定G的起点，即点G′；当点E与C重合时，确定点G的终点，即点G；求GG′.

具体解题过程如下：

解在矩形ABCD中，因为AD=23AB=4，所以AB=6.由题意得AF=AB=6.如图2，过点G作GH⊥AD，交AD的延长线于点H.

因为AG是∠DAF的平分线，所以∠GAH=∠GAF，所以△AGH≌△AGF.

从而可得AH=AF=6，DH=2.

因此点G在过点H且平行于DE的直线上运动，当点E与B重合时，G′是G的起点，如图3所示；当点E与C重合时，点G为终点；点G的运动路径为线段GG′.设GH=x，那么GG′=6-x，GF=x，CG=4+x.易证G′H=AB=6，DH=CG′=2.在Rt△GG′C中，由勾股定理得CG′2+GG′2=GC2，即22+（6-x）2=（4+x）2.求得x=1.2，GG′=6-x=4.8.即点G的运动路径长为4.8.

本题选择矩形为图形载体，通过图形的“翻折”运动以及“动点”运动，设置问题，让学生经历从“特殊”到“一般”、从“静”到“动”的探索过程，注重对学生能力的考查，在解决问题的过程中，培养学生的自主探究能力和解决问题的能力.通过确定运动的起点和终点来确定动点运动的路径长度，为随之而来的计算推理过程打好基础.“以不变应万变”是解决数学“动点”探究题的基本思路，这也是动态几何数学问题中最核心的数学本质.

2 在单元教学中体验初中数学“动点问题”的关键词“以不变应万变”是初中数学“动点问题的”关键词.当下流行的“单元教学”对于学习“动点问题”来说，优势显而易见.在新课程标准指引下，单元教学需要将教学内容与相关知识、技能和基本经验关联起来，以形成相关知识结构体系.初中数学“动点问题”单元教学的主要步骤有：第一步，选取教学内容；第二步，确定素养培养目标；第三步，教学设计；第四步，设计教学评价.

2.1 选取教学内容

初中数学“动点问题”常见的场景有以下几种：点在三角形（等腰三角形、直角三角形）中运动（4课时）；点在四边形（梯形）中运动（4课时）；点在相似图形中运动（2课时）；点在一般几何图形中运动（2课时）；点在二次函数中运动（5课时）.全部教学任务共需要17课时，与非单元教学相比，所需要学时更少，并且增加了“图形背景”“函数思想方法与应用”等重要内容.这样的单元教学设计有利于培养学生的数学素养，与如今的“双减”政策密切相结合，有效提高学生的学习效率.

2.2 确定素养培养目标

《义务教育数学课程标准（2022年版）》明确指出：义务教育数学课程应使学生通过数学的学习，形成和发展面向未来社会和个人发展所需要的核心素养[3].根据数学课程标准，与现有学情联系到一起，确定以下初中数学“动点问题”培养目标：

2.3 教学设计

单元教学设计的关键在于单元教学内容的整体设计，在进行单元教学设计时需要在“教什么”和“怎么教”这两个方面花功夫.“教什么”是对教学内容的选取与把握，而“怎么教”则考验教师的教学能力.在这里，将“怎么教”浓缩为三个关键词：渗透、提炼和衔接.

“渗透”是教学的第一阶段，即将动点问题的常见模型类型与其中的变量、常量、对应关系等的基本概念互相联系起来；第二阶段是“提炼”，将“动点问题”的核心知识、数学思想方法提炼出来；第三阶段是“衔接”高中知识.由此可见，“渗透”是解决问题的基础，“提炼”是解决问题的关键，而“衔接”则是问题解决后数学知识能力的升华.

2.4 设计教学评价

赵思林等在《数学核心素养的内涵探究》一文中指出：数学核心素养是个体的身体和心理协同作用于数学活动而形成具有“数学头脑”的自组织的数学经验系统[4].数学核心素养既是个体在长期的数学理解、应用、思维、发现（创造）等活动中反复修炼自主生成的过程，也是个体对数学经验不断积累、反省、反证的自我体验过程.初中数学“动点问题”单元教学应将扎实学习“四基”、努力培养“四能”为目标，让学生在获得解决“动点问题”的知识经验、积累解决问题的数学思维的基础上，通过对“动点问题”学习经验的不断反思、反证等思维方式，培养学生“动点问题”的“三会”素养.

3 关于初中“动点问题”单元教学的建议

教学设计能力和课堂教学能力是考查教师业务能力的重要指标.高质量的教学设计需要深入贯彻单元教学的理念，从整体的角度让学生体验大单元教学的优势，让学生更好地掌握“动点问题”的解决手段与方法.此外，在进行教学设计时，要突出“育人”的核心思想，找准“育人”的切入点.需要特别注意的是，在数学课堂教学过程中，针对相关典型例题的教学活动不能仅以单一的解题形式呈现，而是需要体现出活动的具体目标、具体任务、具体方式等，必要时还需要教师在活动过程中进行指导和评价.

在课堂教学环节，建议从以下方面提高教师对“动点问题”的认识水平和教学能力：在进行“动点问题”的教学设计时，要让学生认识到具体的“动点问题”与相应的数学模型之间的联系；要让学生的学习过程被充分关注到，并能及时对学生的学习方式和学习方法进行指导，让不同水平的学生参与到学习的过程中来，从而让数学的“育人”价值得到体现；要让教学目标在预设与生成之间得到呼应，充分激发学生的数学学习兴趣；要精心设计有效的“问题串”，通过有梯度的问题，让学习进程“缓而不慢”.

参考文献：

［1］ 刘珠伊.几何画板辅助平面几何中动点问题的教学实践研究[D].长沙：湖南师范大学，2019.

[2] 徐菊萍. 借助几何画板，巧妙破解“与圆有关的位置关系”动点型策略[J]. 苏州教育信息化，2016（4）：17-20.

[3] 中华人民共和国教育部.义务教育数学课程标准[M].北京：北京师范大学出版社，2022.

[4] 趙思林，高峥，熊露.数学核心素养的内涵探究[J].内江师范学院学报，2020（6）：12-17.

［责任编辑：李璟］