基于LSTM与seq2seq模型的短期电力负荷预测方法

2023-12-18李建芳张海峰赵晓龙陈润东

电子设计工程 2023年24期

李建芳，纪鑫，张海峰，赵晓龙，陈润东

（1.国家电网有限公司大数据中心，北京 100052；2.北京国网信通埃森哲信息技术有限公司，北京 100052）

由于工业、农业以及人们日常生活中使用的电器数量增加，电力系统产生的电力负荷随之增加[1]。为了向生产和生活提供可靠、安全的电力能源，有必要对短期电力负荷进行预测，并根据预测结果调整电力系统的发电量，尽量达到收支平衡。

电网的运行特性、容量决策、自然条件、社会影响等都是影响电网负荷预测结果的重要指标。准确的负荷预报数据，不但可以提高电网的运行安全，而且可以极大地减少电网的运行费用，节省能源。现阶段发展较为成熟的短期负荷预测方法应用了注意力机制、神经网络等算法，然而传统方法在实际应用过程中，预测准确率较低，影响了预报的可信性。为了解决上述传统预测方法存在的问题，文中引入LSTM 与seq2seq 模型。通过LSTM 和seq2seq 算法的融合构建模型，并将其应用到短期电力负荷预测方法的优化设计工作中，以期提高电力负荷的预测精度以及应用价值。

1 短期电力负荷预测方法设计

电力短期负荷预测是将历史负荷资料向未来时间进行预测，运用统计学、人工智能、经验分析等量化手段，揭示电网的负荷变化，并对其进行预测[2]。负荷的变化具有随机性，受环境、人为、天气、经济等因素的影响而实时发生变化。所以，在对电网的短期负荷进行预报时，必须充分地综合以上各种影响因子和历史负荷的变化情况。

1.1 收集历史电力负荷数据

短期电力负荷数据的构成具有时间特性，可以将任意时刻的电力负荷表示为：

式中，Ln为基础负荷，Lw为天气影响系数，Ls为经济影响系数，Lr为发电噪声值。其中，Ln的量化计算公式如下：

式中，κ(t) 为负荷分量与时间之间的线性变化系数，Z(t) 为负荷的周期变化系数。根据式（1）的结构，在电力管理系统数据库中，采用数据挖掘技术提取预测时间前三个月的电力负荷数据作为历史数据[3]。在数据补全、异常处理和标准化处理等步骤的实施下，确保了电网的短期负荷预报准确率[4]。采用线性差分法来解决小间距的数据丢失问题。线性差分数据处理过程可以表示为：

式中，xn和xn+1分别为n和n+1 时刻的电力负荷，xn+k表示中间缺失负荷数据的补充结果，i表示负荷数据集长度。标准化的输入数据主要用于衡量各种指标的比例，而在输出数据上则是使其能够更好地反映负载的变化趋势[5-6]。历史负荷数据的归一化计算式如下：

式中，ximin和ximax分别为历史负荷数据集i的最大值和最小值，xi为历史负荷数据的采集值，为数据的归一化处理结果[7]。根据以上步骤处理初始数据，得到精确的历史电力负荷数据。

1.2 利用LSTM与seq2seq模型提取电力负荷变化规律

1.2.1 构建LSTM与seq2seq模型

LSTM 的基础架构包括输入门、输出门和遗忘门三个部分，三个门控制进出单元的信息。LSTM 单元结构原理如图1 所示。

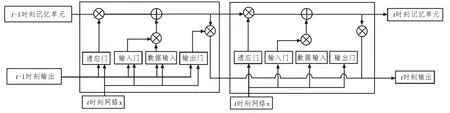
图1 LSTM单元结构原理

LSTM 把各个记忆单元连在一起，确保每一个记忆单元的数据都能在不改变的情况下进行传输[9]。利用LSTM 的三种门控结构对数据的选择性转移进行控制，Sigmoid 函数的输出是[0,1]区间内的数字。遗忘门负责在ct中删除并保存前一时间的有效信息，遗忘门的计算处理过程可以表示为：

式中，σ()∙表示Sigmoid 激活函数，ωf为权重值，ht-1和xt分别为上一时刻LSTM 的输出值以及当前LSTM 的输入值，bf表示偏置项。输入门将当前时刻有效的信息存放在状态单元中，决定了细胞状态的更新，输出门的细胞状态更新过程可以表示为：

式中，tanh()∙为记忆单元更新函数，ωc、xt和bc分别对应输出门的权重值、输入值以及偏置值。输出层确定了LSTM 神经单元所需的信息，并在此基础上，利用所保存的遗忘门和输入门的信息，生成新的单元，并将新的单元传送到tanh 函数，由Sigmoid 确定当前时间隐藏层的输出值，最后LSTM 模型的输出结果如下：

式中，变量ot和it分别表示输入门和输出门的输出结果。

seq2seq 模型解码端接收到编码部分的最后状态，将每个步骤的输出值作为下一阶段的输入值。通过LSTM 模型与seq2seq 模型的构建与组合，完成模型的构建[10]。seq2seq 模型的运行以LSTM 模型隐含层状态的输出结果作为输入序列，在此基础上通过编码与译码处理，得出最终的特征提取结果。

1.2.2 提取电力负荷变化特征

将收集的历史电力负荷数据代入到构建的LSTM 与seq2seq 模型中，分别从负荷峰值、负荷谷值、负荷均值等方面，提取历史电力负荷的变化特征。以负荷峰值为例，模型输出的特征提取结果可以表示为：

式中，变量xi和y分别为负荷影响因子和电力负荷分量，X(xi,y)为收集的历史电力负荷数据集，J为历史数据量[11]。同理可以迭代计算得出历史电力负荷数据其他特征的提取结果。通过对单位时间内电力负荷数据变化特征的提取与分析，确定该区域内电力负荷的周期性浮动规律。

1.3 分析短期电力负荷影响因素

影响短期用电负荷的因素包括气候、电价等，气候因素具体包括温度、湿度、风速等。在夏季大量使用大功率的制冷设备，造成了一定时期内的负载迅速增长，从而产生了较高的负载高峰[12-13]。以温度影响因素为例，其影响机理可以表示为：

式中，λT为温度影响系数，ΔT表示温度浮动值，Lt0和Ltn分别对应t0和tn时刻的电力负荷值。通过对历史电力负荷以及温度数据的分析，确定λT的具体取值[14]。同理可以得出电价因素以及其他因素对电力负荷数据的影响关系。

1.4 实现短期电力负荷预测

综合短期电力负荷的周期性变化规律以及预测时间节点的影响因素，得出短期电力负荷的预测结果为：

式中，变量λ为综合影响系数，tforecast和tcurrent分别对应电力负荷的预测时间节点和当前时间节点，χ为历史电力负荷的变化规律系数[15-16]，该系数的具体取值由LSTM 与seq2seq 模型的特征提取结果决定。按照上述方式，可以得出电力系统任意时刻的短期电力负荷的预测结果。

2 实验分析

以Inteli52.70 GHz CPU、NvidiaGeforce2080Ti*4和256 GB 内存的服务器进行模型构建和负荷数据预测，并设计预测性能测试实验。在实验环境中安装Keras 工具，该工具支持LSTM 与seq2seq 算法的直接调用。为了体现出优化设计短期电力负荷预测方法的性能优势，实验设置了传统的基于自组织特征神经网络和最小二乘支持向量机的短期电力负荷预测方法（方法一）作为对比方法。通过相关数据的统计与对比，体现出优化设计方法的预测性能优势[17]。

2.1 短期电力负荷实验数据集

此次实验选择了三个数据集用作负荷预测的训练和测试。分别从某省三个地区电力公司官网下载负荷数据，实验选择2022 年3 月1 日-3 月15 日的数据，数据的采样周期为1 小时，共计6 000 个样本。负荷数据样本中包括工作时间负荷和休息时间负荷。在神经网络算法中，数据经过处理后，要对数据进行分割，然后再将其输入到模型中进行训练。若将所有的样本数据都投入到模型中，会导致模型与整体数据的拟合过度，从而影响到预测结果的准确性，所以将数据按8∶2 的比例划分为两个数据子集。

2.2 设置LSTM与seq2seq模型运行参数

由于优化设计的短期电力负荷预测方法应用了LSTM 与seq2seq 模型，为保证优化设计的预测方法能够在实验环境中正常运行，分别针对LSTM 模型和seq2seq 模型的运行参数进行设置。LSTM 的基本参数分为基本参数和超参数两种。基本参数的初始权重被设定为[0,1]之间的任意分布，将隐藏层的层数设定为5、超参数中的批次尺寸设定为64，模型设置学习率的初始值为0.000 1，并在训练期间根据数据的收敛性来调整。选用枚举法逐层选取seq2seq 模型中的隐藏单元参数。

2.3 设定预测性能测试指标

实验设置预测误差来反映预测方法的运行性能，其中预测误差的数值结果为：

式中，Lactual_t和Lforecast_t分别为t时刻的实际电荷值和预测电荷结果，参数T为预测目标时段。计算得出ε的值越大，证明短期电力负荷预测性能越优。

2.4 实验过程与结果分析

选择2022 年4 月1 日和2 日电力负荷作为短期电力负荷的预测目标，预测时间分别为工作日和休息日，通过LSTM 与seq2seq模型以及短期电力负荷预测方法的运行，得出电荷预测精度结果如表1 所示。

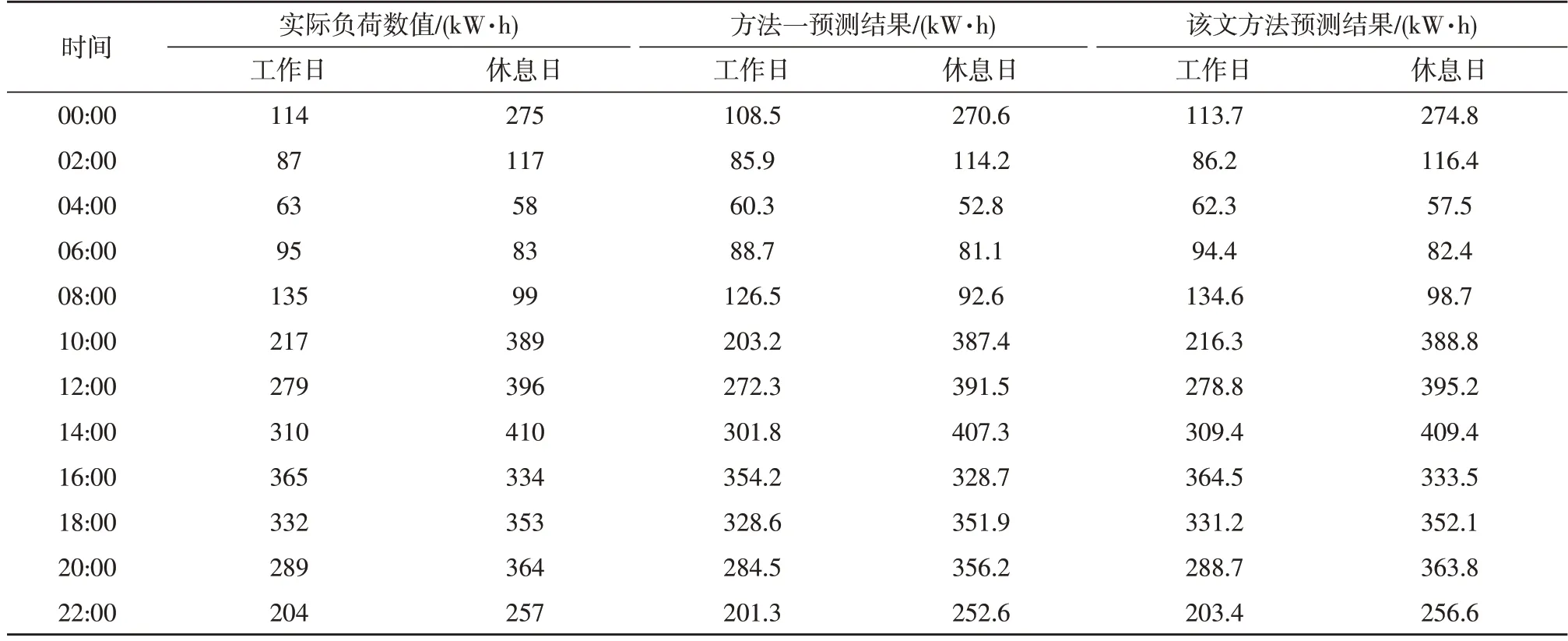
表1 短期电力负荷预测精度测试数据表

将表1 中的数据代入式（11）中，得出传统预测方法的工作日和休息日电力负荷的平均预测误差分别为6.18 kW·h 和4.01 kW·h，而优化设计预测方法在两个工况中的电力负荷平均预测误差分别为0.54 kW·h 和0.48 kW·h。由此可见，综合工作日和休息日两种情况，优化设计的基于LSTM 与seq2seq模型的短期电力负荷预测方法的预测误差更低，证明该方法的预测性能更优。