基于簇间连接的元聚类集成算法

杜淑颖 ,丁世飞 ,邵长龙

（1.中国矿业大学计算机科学与技术学院，徐州，221116；2.徐州生物工程职业技术学院信息管理学院，徐州，221000）

聚类是数据挖掘领域中热门的研究课题之一，其研究目的是根据相似性的大小把数据分到不同的簇中，使簇内数据之间的相似性尽可能大，簇间数据之间的相似性尽可能小［1］.目前聚类已被运用在各种领域，如图像处理［2］、社区发现［3］、数据挖掘等等［4］.过去几十年中，人们开发了大量的聚类算法，比较具有代表性的有谱聚类［5-6］、密度峰值聚类［7-8］、自适应聚类等［9-10］，每种聚类算法都有其自身的优点.但目前的聚类算法仍然存在一些问题，如聚类结果很大程度上取决于参数及其初始化、聚类结果不够稳健等.为了解决这些问题，研究者提出了聚类集成算法.

与通常使用单个算法生成单个聚类结果的传统做法不同，聚类集成是整合多个不同的聚类结果来生成更好更稳健聚类结果的过程.聚类集成算法的有效性使其越来越受到关注，许多相关算法被提出.这些算法可分为三大类，即基于共关联矩阵的算法、基于图分区的算法和基于中值聚类的算法.

基于共关联矩阵的算法根据数据点与数据点之间在相同簇中共现的频率得到一个共关联矩阵，以该矩阵作为相似度矩阵，采用层次聚类的算法得到最终结果.Fred and Jain［11］首次提出共关联矩阵的概念，并据此设计了证据集聚聚类（Evidence Accumulate Clustering，EAC）算法.Wang et al［12］对EAC 算法进行扩展，考虑到簇的大小，提出概率集聚算法.Rathore et al［13］利用随机投影对高维数据进行降维，并利用共关联矩阵设计了一种针对于模糊聚类的聚类集成算法.Zhong et al［14］认为删除共关联矩阵值较小的项可以提高聚类效果，并猜想哪些项中可能包含大量噪声.

基于图分区的算法将聚类集成的信息构成一个图结构，再利用图分割算法将图分割成若干块，进而得到最终的聚类结果.Strehl and Ghosh［15］将聚类成员里的每个簇都作为一个超边缘，构造了三种超图结构，再用METIS 算法对其进行图分割，得到最终的聚类结果.Fern and Brodley［16］将聚类成员构造成二部图，其中对象和簇都表示为图节点，只有当其中一个节点是对象，另一个节点是包含它的簇时，二部图的值才不为0，并用Ncut算法对其进行分割.Huang et al［17］提出一种针对大规模数据的基于采样的谱聚类算法，并设计了一个二部图对其进行聚类集成.

基于中值聚类的算法将聚类集成问题建模成一个最优化问题，其优化目标是寻找一个与所有聚类成员最相似的聚类结果，这个聚类结果被视为所有聚类成员的中值点.这个问题已经被证明是一个NP 难问题，所以在全局聚类空间里寻找最优解在较大的数据集上是不可行的.为此，Cristofor and Simovici［18］利用遗传算法求聚类集成的近似解，其中聚类被视为染色体.Topchy et al［19］将中值聚类问题转化为极大似然问题，并用EM（Expectation Maximization）算法求解.Huang et al［20］将聚类集成问题转化为二元线性规划问题，通过因子图模型进行求解.

尽管取得了重大的进展，但目前的研究仍然存在两个挑战性问题：首先，目前的算法大多是在对象级别对集成信息进行研究，往往无法从簇的层面集成更多的信息；其次，多数聚类集成算法仅仅关注了聚类成员的直接连接，忽略了聚类成员的间接连接.

在聚类集成的过程中，对象间的直接共现是最容易捕捉的信息，Fred and Jain［11］提出共关联矩阵的概念，用两个对象在同一簇中共现的次数作为它们的相似度.但是现实情况远比此更复杂，图1 列出了几种可能出现的情况.

图1a 中，两个对象在同一簇内，则这两个对象可以被认为是同一类.图1b 中，两个对象分属于两个有公共部分的簇，可以用Jaccard 系数计算两个簇之间的相似度，这两个对象也被认为有一定的可能性在同一类中.图1c 中，两个对象分属于两个不相连的簇，但这两个簇均与第三个簇有联系，这种簇间间接相连的情况，很难度量这两个簇之间的相似性，也很难对这两个对象进行分类，这就需要对隐藏在簇间的间接关系进行发掘利用.针对这个问题，本文提出一种基于簇间连接的元聚类集成算法（Link-Based Meta-Clustering Algorithm，L-MCLA）.

1 相关工作

1.1 聚类集成聚类集成是通过整合多个聚类结果来提高聚类效果的算法，通常可以表述如下.

给定一个具有n个数据对象的数据集X={x1，x2，…，xn}，对此数据集X使用m次聚类算法，得到m个聚类结果P={p1，p2，…，pm}，其中，pi(i=1，2，…，m)为第i个聚类算法得到的聚类结果，又被称为聚类成员或基聚类.具体地，聚类成员的生成有三种算法：

（1）使用一种聚类算法，每次运行时随机设置不同的参数并随机初始化.（2）使用不同聚类算法产生不同的聚类成员.（3）对数据集进行采样，得到不同的子集，再对子集进行聚类，得到不同的聚类成员.

每个聚类成员包含若干个簇，记作pi=，其中，j是聚类成员pi里包含簇的个数.聚类集成就是对集合P通过一致性函数T进行合并，得到数据集X的最终聚类结果P*.聚类集成的具体流程如图2 所示.

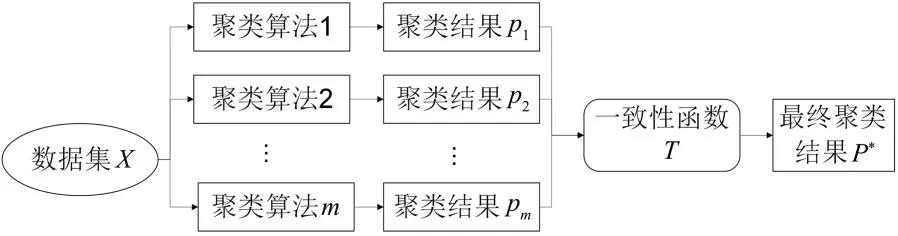
图2 聚类集成流程示意图Fig.2 The flowchart of clustering ensemble

1.2 元聚类2003 年，Strehl and Ghosh［15］提出被称为“元聚类”（Meta-Clustering Algorithm，MCLA）的聚类集成算法，其中心思想是对簇进行分类，而不是对对象进行分类，最后，将对象分配到最有可能归属的簇群中.元聚类算法利用Jaccard 系数计算簇间的相似度，假设有簇Ci和Cj，它们之间的Jaccard 系数的计算如下：

其中，| |代表集合中点的个数.

接着，元聚类算法对得到的相似度矩阵利用METIS 图划分进行分类.METIS 是一种多级的快速图分割技术，在元聚类算法里利用它将簇分成若干个簇群［21］，每个簇群被称作元簇群（Meta-Cluster，MC）.最后，将对象分配到对应的元簇群，得到聚类结果.元聚类算法的四个步骤如下.

（1）构造相似度矩阵：将M个聚类成员包含的全部簇都当作矩阵节点，计算簇和簇之间的Jaccard 系数作为矩阵的值，构造相似度矩阵.

（2）生成元图：将矩阵节点当作图节点，将矩阵的值当作图的边，将上一步的相似度矩阵看作一个无向图，称为元图（Meta-graph）.

（3）划分元图：使用METIS 图划分算法对上一步的元图进行划分，得到K个元簇群，每个元簇群都包含若干簇.

（4）对象分配：将数据对象分配到对应的元簇群得到最终结果.具体地，基于投票法，将对象从属于元簇群中簇的次数与元簇群中簇的总个数的比看作对象从属于这个元簇群的可能性.对于一个对象，将它分配到可能性最大的元簇群中，进而得到最终结果.

Strehl and Ghosh［15］用一系列实验证明了元聚类算法的优越性和鲁棒性，使其成为一个经典的聚类集成算法.

1.3 连接三元组元聚类算法虽然优越，但仍有一个缺点，就是利用Jaccard 相似度来构建的相似度矩阵仅仅能反映簇与簇之间的直接联系，无法进一步挖掘其中的间接关系.对于那些没有公共部分的簇，它们的相似度只能为0，忽略了它们之间的弱联系性.

2011 年，Iam-On et al［22］提出加权连接三元组（Weighted Connected-Triple，WCT）的概念来挖掘簇与簇之间隐藏的间接关系，其基本思想是：如果两个节点都与第三个节点有连接，则认为这两个节点之间也有一定的关系，第三个节点被称为这个三元组的中心.通过这种算法可以找到簇与簇之间的间接连接，进一步丰富原来的相似度矩阵包含的信息，进而得到更好的聚类结果.

连接三元组因为其较好的特性被运用在许多研究中.周林等［23］将连接三元组运用在谱聚类中，提出一种基于谱聚类的聚类集成算法.张恒山等［24］将其与群体智慧相结合，提出一种新的聚类集成算法.证明使用连接三元组可以有效地挖掘簇之间隐藏的信息，有利于提高聚类结果.

2 L-MCLA 算法

2.1 构建相似性矩阵本节利用连接三元组（如图3 所示）来构建细化的簇相似性矩阵.

图3 连接三元组的示意图Fig.3 The schematic diagram of connecting triples

首先，用Jaccard 系数计算簇与簇之间的相似度，如式（1）所示.

设Ck与Ci和Cj都有相似度，则Ci和Cj之间的连接三元组定义如下：

簇Ci，Cj之间的相似度SimWCT(i，j)计算如下：

其中，C是簇的总集合.

对于簇集合C中任意的两个簇Ci和Cj，它们之间的相似度可以定义为：

其中，DC为衰减因子，即为两个不同事物的相似程度的置信水平.

通过式（4）可以构建一个信息更丰富的簇相似度矩阵，有利于后面得到更好的结果.

2.2 一致性函数一致性函数包含图划分和对象分配两个步骤.首先，将优化后的相似度矩阵S视为邻接矩阵，构建一个无向图G，即：

其中，V=C，将全部的簇看作图像中的点.L=Sim(i，j)，将簇之间的相似度看作无向图的边，这样就构建了一个无向图.

然后，将这个无向图G通过图分区算法分为K个部分.在图分区算法的选择中，由于归一化割（Normalized Cut，Ncut）［25］的优越特性，本研究选择它作为图分区算法.

通过Ncut 可以得到K个元簇群，每个元簇群都由若干个簇构成.即：

接着，使用投票法将对象分配到对应的元簇群中.对于给定的一个对象xi，xi可能属于MCj中的零个或多个簇，即可以用对象xi从属于MCj中簇的次数与MCj中簇的总个数的比来定义xi属于元簇群MCj的可能性.具体地：

其中，|MCj|代表元簇群MCj中 簇的个数.

对MC中的每个元簇群MCj求得一个分数，将点xi分配到得分最高的元簇群里，完成对象分配.

L-MCLA 算法描述如下.

2.3 算法的复杂度分析首先看时间复杂度.因为第一步生成聚类成员的时间复杂度与基聚类算法有关，在此不做分析.第二步生成相似度矩阵Z的时间复杂度为O()，其中，NC为聚类成员包含的簇的总数.第三步用连接三元组对相似度矩阵Z进行细化，时间复杂度是O()，其中，m为聚类成员的规模.第四步将相似度矩阵WCTZ看作一个无向图G，无向图G包含2NC个节点，使用Ncut 算法进行分割的时间复杂度是，其中，K是图分割的块数.第五步对对象进行分配，时间复杂度是O(KNNC)，其中，N为对象个数.所以，本文算法的总的时间复杂度最大为：

生成相似度矩阵的空间复杂度为O()，这也是本文算法空间复杂度的主要来源，其余步骤所占空间远小于这个值.故可以认为本文算法的空间复杂度为O().

3 实验结果与分析

在多个实际数据集中与现有的聚类集成算法进行对比实验来验证本文算法的有效性，并通过对不同聚类成员规模的比较来证明本文算法的鲁棒性.

3.1 数据集和评价标准使用UCI（University of California Irvine）机器学习数据库中的八个数据集为实验数据集进行对比实验.表1 列出了数据集的详细信息.

选择ARI（Adjusted Rand Index）和NMI（Normalized Mutual Information）来评价聚类结果.

ARI通过计算样本点对位于同一类簇和不同类簇的数目来度量聚类结果之间的相似程度，计算如下：

其中，a表示在真实情况下和实验中都属于一个簇的点对数目，b表示在真实情况下是一个簇而在实验中不是一个簇的点对数目，c表示在真实情况下不是一个簇而在实验中是一个簇的点对数目，d表示在真实情况下和实验中都不属于同一个簇的点对数目.ARI的取值范围为[-1，1]，值越大表明和真实结果越吻合，即聚类效果更好.

NMI是常见的聚类有效性的外部评价指标，从信息论的角度评估两个聚类结果的相似性.设实验结果为X，真实结果为Y，NMI的计算如下：

其中，I(X，Y)表示X和Y之间的互信息，H(X)和H(Y)表示变量X和Y的熵.NMI的取值范围为[0，1]，值越大表明和真实结果的共享信息越多，即聚类效果越好.

3.2 对比实验和实验设置使用七种聚类集成算法与L-MCLA 算法作对比：EAC（Evidence Accumulation Clustering）［11］，HBGF（Hybird Bipartite Graph Formulation）［16］，WEAC（Weighted Evidence Accumulation Clustering）［26］，GP-MGLA（Graph Partitioning with Multi-Granularity Link Analysis）［26］，CSPA（Cluster-Based Similarity Partitioning Algorithm）［15］，HGPA（Hypergraph Partitioning Algorithm）［15］，MCLA（Meta-Clustering Algorithm）［15］

对比算法的选择，首先是本文改进的元聚类算法MCLA 以及与其相关的CSPA，HGPA，还有聚类集成领域的经典算法EAC，HBGF 以及近年来的新算法WEAC，GP-MGLA，这些对比算法使实验结果具有一定的说服力.对比算法的参数按文献给出的参考值进行设置.

实验环境：Windows 7 64 位操作系统，英特尔i5 双核 1.7 GHz 中央处理器，8 G 内存，在MATLAB R2016a 中实现.

实验中首先要生成包含m个聚类成员的聚类集合，使用k-means 算法生成聚类成员，每个聚类成员的生成均采用随机初始化，并在中随机选取k-means 的聚类个数k.称聚类成员个数m为聚类集成规模，固定聚类集成规模m=50，分别将本文算法与其他聚类集成算法进行比较，再在不同聚类集成规模下测试本文算法的聚类表现.

3.3 聚类集成算法的对比实验在每个数据集中每个聚类集成算法均运行20 次，每次运行根据3.2 随机生成聚类成员，得到聚类结果后计算ARI和NMI的均值及其标准差.实验结果如表2和表3 所示，表中黑体字表示结果最优.

表2 不同算法的聚类结果的ARI 比较Table 2 ARI of clustering results by different algorithms

表3 不同算法的聚类结果的NMI 比较Table 3 NMI of clustering results by different algorithms

由表2 可见，L-MCLA 算法在八个数据集上的聚类结果的ARI都是最高的.由表3 可见，LMCLA 算法在六个数据集上聚类结果的NMI也都是最高的，仅仅在CTG 和Ionosphere 上略有逊色，不过数值相差不大.

通过以上实验可以证明，本文提出的算法在聚类集成上的优势，和其他的聚类集成算法相比，性能更优.

3.4 聚类集成规模对聚类结果的影响研究不同的聚类集成规模对L-MCLA 算法聚类结果的影响.在八个数据集上取不同数量的聚类成员进行集成.聚类成员规模为[10，100]，以10 递增.聚类成员的生成设置与3.2 相同，取10 次实验结果的平均值作为最终的结果.图4 和图5 显示了在不同聚类集成规模下L-MCLA 算法的ARI和NMI的变化情况.

图4 当聚类集成规模不同时L-MCLA 算法在八个数据集上的ARIFig.4 ARI of L-MCLA on eight datasets with different scales of the clustering ensemble

图5 当聚类集成规模不同时L-MCLA 算法在八个数据集上的NMIFig.5 NMI of L-MCLA on eight datasets with different scales of the clustering ensemble

图4 展示了在聚类集成规模不同时，LMCLA 算法在八个数据集上聚类结果的ARI.由图可见，在大部分数据集上，L-MCLA 算法的聚类结果仅有小幅波动，并在集成规模达到40 以后逐渐趋于平稳，只在Thyroid 数据集和Soybean 数据集上存在不同.在Thyroid 数据集上，L-MCLA算法的聚类结果的ARI在集成规模为10～20 时急剧上升，随后，随着聚类成员的增加呈现一种波动上升的状态.在Soybean 数据集上，随着基聚类的增多，L-MCLA 算法的聚类结果的ARI缓慢下降，但幅度较小.

图5 展示了在聚类集成规模不同时，LMCLA 算法在八个数据集上聚类结果的NMI.由图可见，除了Thyroid 数据集外，L-MCLA 算法的聚类结果在大部分数据集上的NMI均趋于平稳.在Thyroid 数据集上，L-MCLA 算法的聚类结果的NMI在基聚类为10～40 时大幅上升，在40～50时略微下降，随后又上升且逐渐平稳.

通过以上的实验结果和分析可知，聚类集成的规模对L-MCLA 算法的聚类结果的影响不大，在大多数数据集中，L-MCLA 算法可以仅仅依靠较少的聚类成员就得到较稳健的结果.

4 结论

本文提出基于簇间连接的元聚类集成算法，利用连接三元组来探寻簇间相似度，进一步丰富了相似度矩阵的信息，再通过Ncut 算法和对象分配得到最终的结果.

本文提出的算法的优势如下.

（1）从簇的级别考虑集成信息，充分考虑了簇与簇之间的关系.

（2）利用连接三元组增加相似度矩阵中的信息，使聚类结果更准确.

将本文提出的算法与七种聚类集成算法进行了对比实验，证明本文算法和其他聚类集成算法相比，性能存在优势.