循环荷载下单面外包混凝土剪力墙栓钉剪力需求
2023-12-15倪萍,顾强
倪 萍,顾 强
(苏州科技大学 土木工程学院,江苏 苏州 215011)
C-PSW/CE 是在钢墙板一侧或两侧外包混凝土板,两者通过栓钉连接形成整体。混凝土板能够约束钢板过早发生屈曲,从而实现钢板受剪屈服后再发生弹塑性屈曲的破坏模式。C-PSW/CE 的抗侧刚度大、抗剪承载力高、延性较好,是多层或高层钢结构的一种高效抗侧力构件。
到目前为止,已有的文献对C-PSW/CE 的整体滞回性能和混凝土板厚度需求进行了研究,而对栓钉剪力需求的研究较少。Dey[1]从理论上推导了C-PSW/CE 最小混凝土板厚和最大栓钉间距的计算公式。AISC 341-16 规定了C-PSW/CE 的最小混凝土板厚、最小配筋率和最大栓钉间距[2]。齐益等[3-4]提出了单调侧向荷载下双面外包混凝土C-PSW/CE 栓钉剪力需求计算公式。王华飞等[5-6]提出了循环荷载下双面混凝土板CPSW/CE 栓钉剪力需求及混凝土板厚需求计算公式,其满足层间侧移角2%时C-PSW/CE 的承载力不低于峰值承载力的85%。C-PSW/CE 有两种类型,即双面外包混凝土及单面外包混凝土。对单面外包混凝土板CPSW/CE 也有多人研究;但是,目前对于循环荷载下单面外包混凝土C-PSW/CE 的栓钉剪力需求尚未见诸文献。本文对单面外包混凝土C-PSW/CE 的栓钉剪力需求进行了研究,可完善C-PSW/CE 的设计方法,为在高烈度区采用单面外包混凝土剪力墙提供技术支撑。
强烈地震下如果限制C-PSW/CE 的钢墙板在2%层间侧移下不发生屈曲,势必需要较大的外包混凝土厚度和较密的栓钉间距,但这很不经济,并将制约C-PSW/CE 在高烈度区的应用。实际上,循环荷载下,只要采用厚度适当的混凝土板及合适的栓钉间距,使钢墙板进入剪切屈服平台后在经历较大的层间侧移时屈曲,由于混凝土板的约束作用,钢墙板仍能通过面内受剪和不完全屈曲拉力场的作用共同抵抗侧力,体现出CPSW/CE 的延性设计。钢墙板屈曲前,栓钉传递钢板与混凝土板之间的相互作用力,协调两者的平面内变形。钢墙板屈曲后,栓钉又可防止钢板屈曲变形导致的混凝土板脱离,协调两者在平面外的变形。在循环荷载作用下,墙体累积损伤,单面设置的混凝土板破坏严重,亟待对循环荷载下延性设计的单侧外包混凝土CPSW/CE 的栓钉剪力需求进行研究。
本文基于循环荷载下C-PSW/CE 的延性设计思路,设计了51 个C-PSW/CE 有限元算例。采用ABAQUS,建立了C-PSW/CE 有限元模型,模拟了钢板单面外包混凝土C-PSW/CE 各组件在循环荷载下的响应。分析了钢板厚度、混凝土板厚度、栓钉间距、栓钉直径及墙板高宽比对栓钉剪力的影响。根据36 个有效算例的模拟结果,拟合了2%层间侧移内墙板强度劣化低于15%的钢板单面外包混凝土C-PSW/CE 栓钉剪力需求计算公式,可用于预估高烈度区C-PSW/CE 延性设计的栓钉剪力需求。
1 C-PSW/CE 有限元模型
单层单跨C-PSW/CE 由钢板、单侧外包的钢筋混凝土板、栓钉、梁柱节点铰接的钢框架组成。混凝土板用栓钉将其连接在钢板的一侧。采用ABAQUS[7]建立了C-PSW/CE 有限元模型,利用现有的试验结果对有限元模型进行了验证,表明有限元模型能较合理地模拟出C-PSW/CE 在循环荷载下的反应。
1.1 材料特性
混凝土本构采用CDP(Concrete Damaged Plasticity)模型,该模型适用于混凝土在循环荷载下的非线性行为,如图1 所示。本文混凝土强度等级为C30,标准立方体抗拉强度为2.01 MPa,标准立方体抗压强度为20.1 MPa,混凝土单轴受压和受拉的应力-应变关系根据我国现行《混凝土结构设计规范》[8]确定;Ec=30 GPa,泊松比0.2;受拉刚度恢复系数ωt为0,受压刚度恢复系数ωc为1,混凝土受压损伤系数dc和受拉损伤系数dt按文献[9]计算。

图1 混凝土本构
根据《钢结构设计规范》[10],钢墙板的本构关系如图2 所示,图中σy为钢材屈服强度,屈服应变为εy。当εst=0.02 时,钢材开始硬化。钢材的杨氏模量Es=206 GPa,泊松比为0.3;硬化模量Et=0.02Es;钢墙板均采用Q235,板厚hs≤16 mm 时,屈服强度为235 MPa;板厚hs在16~40 mm 之间时,屈服强度为225 MPa。钢框架钢材应力-应变关系为理想弹塑性,钢号为Q355,屈服强度为355 MPa。栓钉选用双线性硬化模型表征其应力-应变关系,屈服强度为240 MPa,极限强度为400 MPa,硬化模量Et=0.02Es。钢筋选用理想弹塑性本构来表征其应力-应变关系,材料选用HPB300,其屈服强度为300 MPa,弹性模量Es=210 GPa。

图2 钢墙板本构
1.2 边界条件和单元类型
有限元模型的边界条件如图3 所示。为消除钢框架参与侧向承载,梁柱各连接点铰接。约束钢框架梁、柱单元平面外自由度UZ、URX、URY。约束左柱脚的UX、UY 和右柱脚的UY。对顶梁施加循环侧向荷载,加载制度根据ATC-24 确定[11],当侧移角达到C-PSW/CE 墙体高度的2%时结束加载,加载曲线如图4 所示。
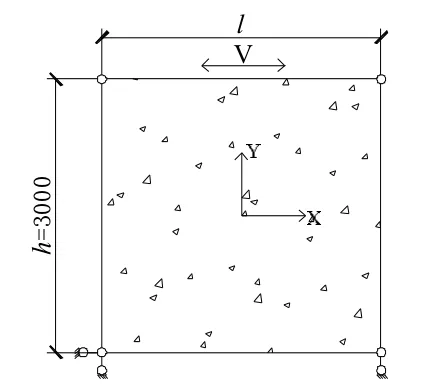
图3 FEM 的边界条件
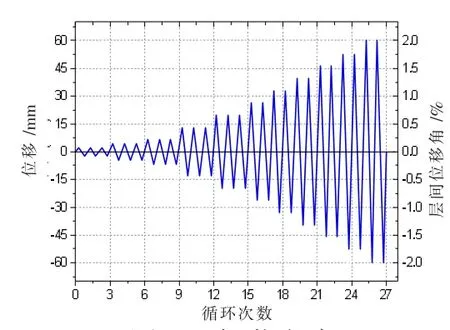
图4 加载方案
钢墙板采用S4R 壳单元;混凝土板采用C3D8R 实体单元;栓钉采用B31 梁单元;边界钢框架采用B31梁单元和S4R 壳单元组合(其中B31 提供框架与钢板之间的相互作用,S4R 模拟梁、柱内翼缘与混凝土板之间的相互作用);钢筋采用T3D2 桁架单元。单元类型如图5 所示。
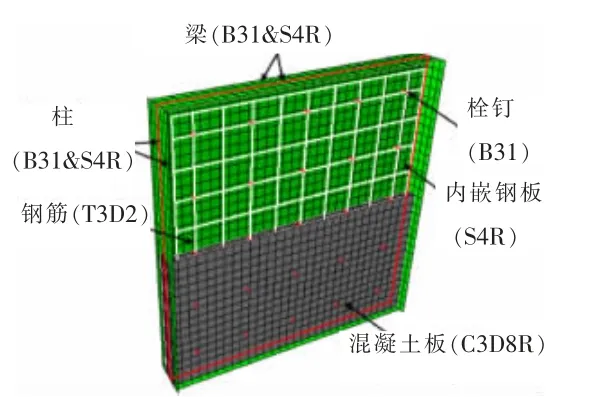
图5 FEM 单元类型
1.3 单元的相互作用
钢墙板(S4R 壳单元)与梁、柱(B31 单元)之间采用“tie”连接。表示梁和柱内翼缘的S4R 壳单元采用“tie”分别连接在梁(B31 单元)和柱(B31 单元)上。为了实现框架铰接,释放框架梁、柱单元公共节点的平面内转动自由度,采用连接单元CONN3D2 耦合位于梁、柱节点处壳单元搭接节点之间的平动自由度,连接属性为“join”。栓钉与钢板之间嵌入连接单元CONN3D2,连接单元属性为“beam”,即耦合了梁单元与壳单元连接处的所有自由度。混凝土板内部的钢筋及栓钉采用“Embedded region”置于其内。对梁、柱内翼缘和混凝土板、钢墙板和混凝土板之间的法向作用采用“硬”接触,切向作用通过设置摩擦系数0.4 来实现,允许接触面自由分离但禁止接触面相互穿透。
1.4 有限元模型验证
采用本文有限元模型对文献[6]的试件W-20 进行模拟,W-20 为钢墙板双侧外包钢筋混凝土板,有限元模型的材料性能、尺寸参数等均与试件W-20 保持一致。现场试验过程中,框架梁柱连接处的销轴与耳板接触部分不可避免地会产生摩擦挤压。为考虑此摩擦挤压影响,有限元模型的梁柱改为S4R 壳单元,梁柱连接的耳板及销轴采用C3D8R 实体单元。
图6 为试件W-20 的有限元模拟曲线与试验曲线的对比。与试验滞回曲线相比,有限元模拟的滞回曲线捏缩程度较轻。主要原因是混凝土的CDP模型不能完全真实模拟试件的混凝土开裂;此外,模拟中采用的混凝土本构关系可能与真实的混凝土本构关系存在差异。这两个原因使得模拟曲线与试验曲线有一定的差异。有限元模拟的卸载刚度与试验曲线大致相同。试件W-20 的抗剪承载力为743 kN,有限元模拟结果与试验结果差异很小,仅为0.4%。可见本文有限元模型能较合理地模拟出C-PSW/CE 在循环荷载下的反应。
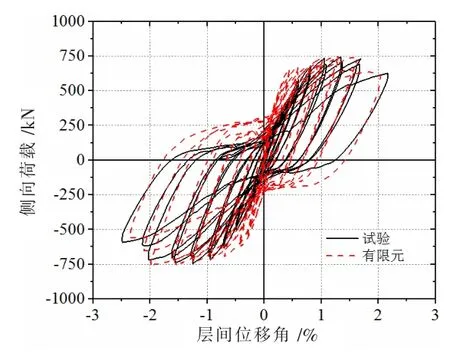
图6 W-20 滞回曲线
1.5 C-PSW/CE 有限元算例
本文C-PSW/CE 有限元算例均为单层单跨,铰接钢框架。墙板高度h 均为3 000 mm。钢梁截面高度均为561 mm,翼缘宽度均为513 mm,腹板厚度均为28 mm,翼缘厚度均为35 mm;钢柱截面高度均为513 mm,翼缘宽度均为513 mm,腹板厚度均为60.5 mm,翼缘厚度均为97 mm。首先根据屈曲分析得到裸钢板的屈曲模态,将一阶屈曲模态作为钢板的初始缺陷加入C-PSW/CE 模型中,初始挠曲朝向无混凝土板的一侧,初曲幅值为h/1000=3 mm。
美国钢结构建筑抗震规范AISC 341-16[2]给出了C-PSW/CE 混凝土板最小厚度、最大栓钉间距以及最小配筋率构造要求。钢板一侧有混凝土板时,混凝土板最小厚度为200 mm。本文混凝土板厚选用200、220、240 mm。双向配筋率ρ 为0.25%。钢墙板厚度选用10、15、20、25 mm。墙板栓钉的水平和竖向间距相等,本文栓钉水平、竖向间距S 为400、350、300 mm。栓钉直径选用13、16、19 和22 mm。墙板高宽比选用1、0.75、0.5。51 个算例详见表1。
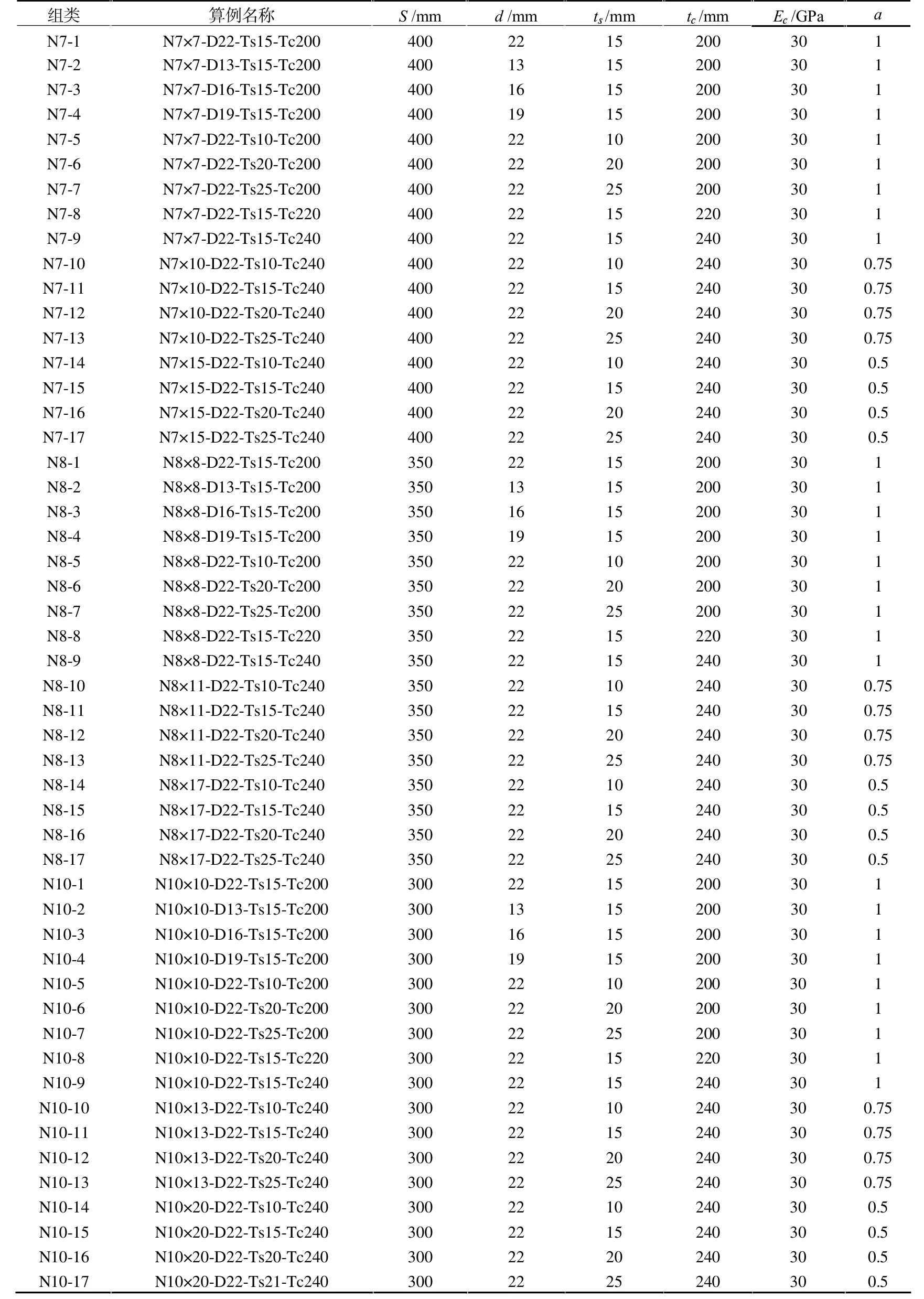
表1 有限元算例
混凝土强度等级为C30。变化的设计参数有栓钉间距、栓钉直径、钢板厚度、混凝土板厚度及墙板高宽比。如表1 中算例N7×7-D22-Ts15-Tc200 的栓钉行列数nr×nc为7×7,即两个方向的栓钉间距均为400 mm,两个方向的栓钉边缘距离均为300 mm;栓钉直径d 为22 mm;钢板厚度ts为15 mm;混凝土板厚度为tc为200 mm;墙体高宽比α 为1.0。
2 循环荷载下C-PSW/CE 响应
经有限元模拟,51 个算例中钢墙板在塑性平台段内发生整体屈曲或局部屈曲,且满足在2%层间侧移内强度劣化低于15%的算例有36 个,下文称这36 个算例为有效算例。本节仅对代表性算例进行介绍。
2.1 C-PSW/CE 滞回曲线
将钢墙板进入剪切屈服平台后发生局部屈曲的算例记为N7×7-D22-Ts10-Tc200-LB。将钢墙板进入剪切屈服平台后发生整体屈曲的算例记为N7×7-D22-Ts15-Tc200-OB。两个算例的钢墙板厚度分别为10 mm和15 mm,其余参数相同;墙板高度h 均为3 000 mm,高宽比α 均为1.0。
图7 为N7×7-D22-Ts10-Tc200-LB 和N7×7-D22-Ts15-Tc200-OB 的钢墙板在层间位移角2%时的面外挠曲图。由图7(a)可知,N7×7-D22-Ts10-Tc200-LB 的钢板在栓钉间距内沿对角线方向形成了一个狭窄的局部屈曲半波;由图7(b)可知,N7×7-D22-Ts15-Tc200-OB 的钢板发生了整体屈曲,沿对角线方向形成了多个较宽的屈曲半波。

图7 钢板的面外变形
图8 为N7×7-D22-Ts10-Tc200-LB 和N7×7-D22-Ts15-Tc200-OB 的剪力-层间侧移曲线,可知钢板发生局部屈曲或整体屈曲前,墙板滞回曲线非常饱满。钢板屈曲后,滞回曲线开始出现捏缩,承载力有一定的下降。对比图8(a)和图8(b)可知,钢板厚度由10 mm 增加到15 mm,钢板的屈曲模式由局部屈曲转为整体屈曲,但发生整体屈曲对应的侧移较局部屈曲有所推迟。
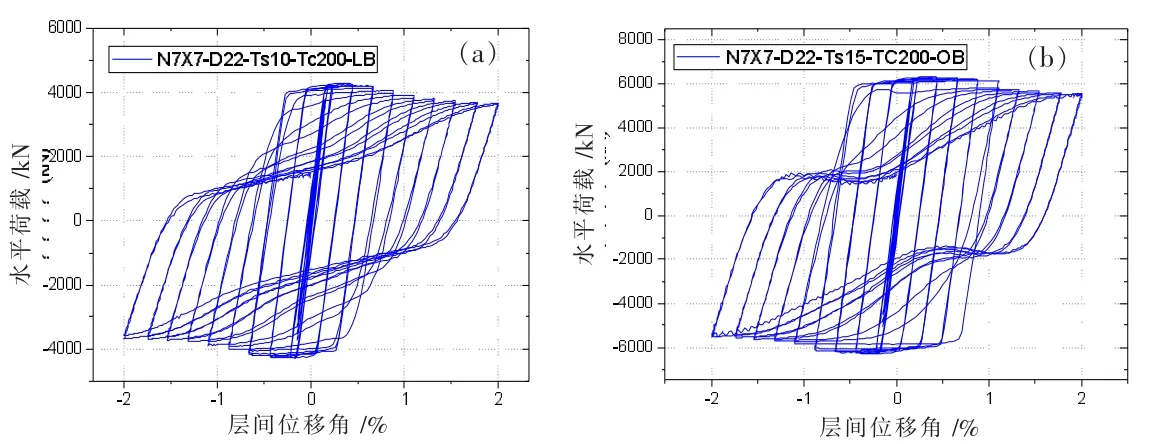
图8 剪力-层间侧移曲线
2.2 钢墙板抗剪机理
钢墙板屈曲前依靠面内剪切抵抗侧向荷载。钢墙板在屈服平台段发生塑性屈曲后,面内剪切与发展不完全的拉力场共同抗侧力。钢板塑性屈曲后的应力状态可由图9 解释,钢板剪应力σyx由面内剪应力τs和拉力场斜拉应力的水平分量τt构成,即钢板顶部截面剪力Vs是钢板面内剪力Vs1和拉力场拉力水平分量Vs2之和,钢板顶部截面的剪力VS=∫(τs+τt)dA=∫τsdA+∫τtdA=VS1+VS2(VS1为钢板平面内剪力,VS2为拉力场的水平分量,A 为钢板顶部截面积);VS可以从有限元计算结果中直接提取;VS1难以直接提取;VS2可以通过对屈曲拉力场应力的垂直分量σyy的积分获得,即(∫σyydA)/VS2=tanθ,其中∫σyydA 可从有限元计算结果中直接提取,θ 为拉力场方向与水平线的夹角;VS1=VS-VS2。式中,A 为钢板顶部横截面面积,θ 为拉力场与水平方向的夹角。
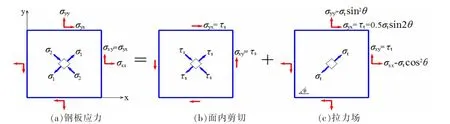
图9 钢板屈曲后的应力状态
图10 为循环荷载下N7×7-D22-Ts10-Tc200-LB 和N7×7-D22-Ts15-Tc200-OB 的钢墙板面内剪力占比Vs1/Vs、不完全拉力场承担剪力占比Vs2/Vs与层间侧移的骨架曲线,图中还给出了钢板的面外挠度与层间侧移角的关系曲线。
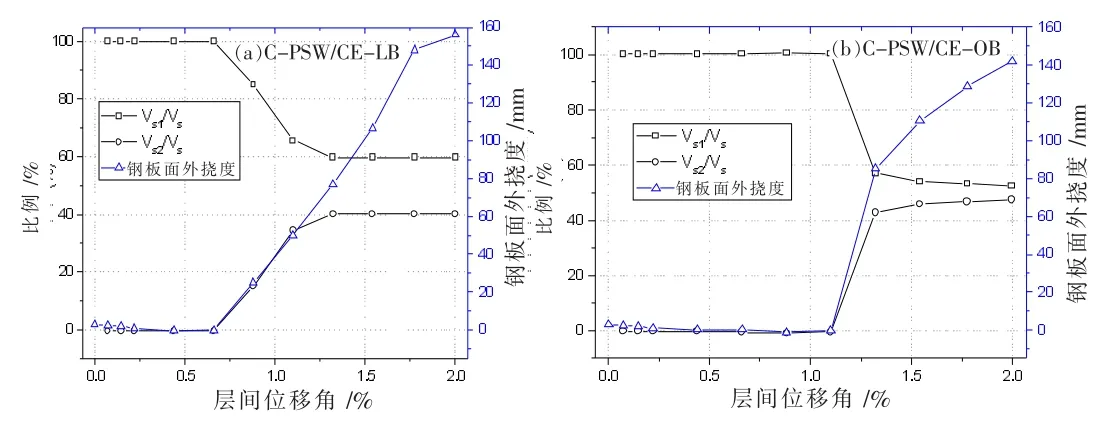
图10 钢板的Vs1/Vs 及Vs2/Vs 和面外变形骨架曲线
由图10(a)可知,当层间侧移角0.67%时,N7×7-D22-Ts10-Tc200-LB 钢板发生局部屈曲,面外挠度开始增大,钢板面内剪力在钢板总剪力中的占比开始减小,局部屈曲拉力场承担的水平剪力开始增大。层间侧移角介于0.67%至1.32%区间时,Vs1/Vs曲线急剧降低,Vs2/Vs曲线急剧升高,钢板面外挠度陡增。层间侧移角介于1.32%至2%区间时,Vs1/Vs和Vs2/Vs变化趋于稳定。层间侧移角为2%时,钢板的主应力矢量如图11(a)所示,钢板内已经形成了明显的对角拉力场,与此同时,拉力场承担的水平剪力占据了钢板总剪力的40.16%,钢板面外挠度值156.075 mm。
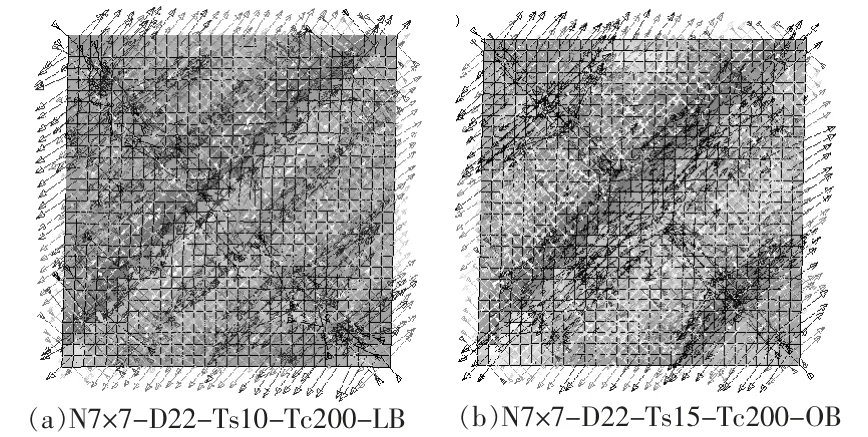
图11 钢板主应力矢量图
由图10(b)可知,当层间侧移角1.1%时,N7×7-D22-Ts15-Tc200-OB 钢板开始发生整体屈曲,面外变形开始迅速增大,与此同时,Vs1/Vs曲线陡降、Vs2/Vs曲线陡增;层间侧移角到达1.32%之后,随着侧移的继续增大,Vs1/Vs和Vs2/Vs曲线变化逐渐趋于平缓,钢板面外变形的增长速度也开始变缓。钢板在层间侧移角2%时的主应力矢量如图11(b)所示,拉力场已占据钢板较大面积,拉力场分担的水平剪力占钢板总剪力的47.47%,钢板面外挠度值141.968 mm。
图12 为N7×7-D22-Ts10-Tc200-LB 和N7×7-D22-Ts15-Tc200-OB 在循环荷载下的剪力-层间侧移骨架曲线。图12 中,Vc为混凝土板分担的水平剪力。由于框架梁柱节点铰接,边框架基本不分担水平荷载,即C-PSW/CE 承担的水平剪力由钢板和一侧的混凝土板分担。混凝土板剪力Vc可由墙板承载力V 减去钢板剪力Vs得到。
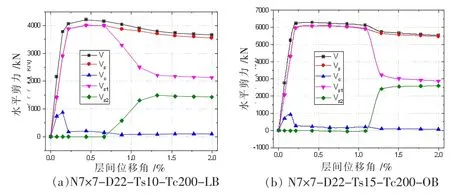
图12 骨架曲线
由图12(a)可知,层间侧移角介于0~0.15%区间时,N7×7-D22-Ts10-Tc200-LB 承载力、钢板分担的剪力、混凝土板分担的剪力呈增大趋势;当层间侧移角到达0.15%时,Vc达到峰值878.871 kN;层间侧移角介于0.15%~0.22%区间时,钢板处于弹性阶段,其分担的剪力继续增大,但混凝土板分担的剪力开始进入下降段,由于混凝土板剪力的下降,墙板承载力增长的速度变缓;层间侧移角介于0.22%~0.66%区间时,钢板处于剪切屈服平台阶段,承载力达到最大值4 005.851 kN,组合墙板承载力也同时达到最大值4 211.49 kN,随后开始有所下降,混凝土板劣化严重;当层间侧移角达到0.66%时,钢板发生局部屈曲,其分担的剪力Vs随之降低,此时钢板面内受剪分担的剪力Vs1开始下降,拉力场分担的剪力Vs2开始增大;层间侧移角介于0.66%~1.32%区间时,钢板屈曲拉力场持续发展,Vs2曲线升高迅速,Vs1曲线急剧下降,钢板总剪力曲线有明显下降,但仍保有较大的承载能力;当层间侧移角介于1.32%至2%区间时,Vs1及Vs2曲线趋于平缓,钢板分担的剪力和组合墙板承载力仍保持缓慢降低;层间侧移角达到2%时,由于混凝土板对钢板屈曲后变形仍有较强的约束作用,组合墙板的承载力仅比峰值承载力劣化了13.14%。
由图12(b)可知,N7×7-D22-Ts15-Tc200-OB 钢板发生整体屈曲前,各曲线发展趋势与图12(a)相似。当层间位移角达到1.1%时,钢板开始整体屈曲,Vs1曲线陡降,Vs2曲线陡增,钢板分担的剪力Vs有明显的下降,组合墙板的承载力也随之降低;当层间侧移角介于1.32%至2%区间时,钢板分担的剪力和组合墙板承载力同步降低,但下降速度明显变缓;层间位移角达到2%时,组合墙板承载力仅比峰值承载力降低了12.07%。
由上述分析可知,在罕遇地震下没有必要采用不经济的较大的混凝土板厚严格限制C-PSW/CE 的钢墙板在2%层间侧移内不能屈曲。只要采用适当厚度的混凝土和适当的栓钉间距,使C-PSW/CE 的钢墙板进入屈服平台后再发生屈曲,混凝土外包仍能约束钢板的屈曲挠度,使C-PSW/CE 的承载力维持在一个较高的水平,实现C-PSW/CE 较经济的延性设计。
图13 为N7×7-D22-Ts10-Tc200-LB 和N7×7-D22-Ts15-Tc200-OB 中钢板和混凝土板分担剪力占比与层间侧移角的关系曲线。由图13(a)可知,N7×7-D22-Ts10-Tc200-LB 在钢板剪切屈服前,钢板承担的荷载与组合墙板承载力的比例曲线Vs/V 随着层间侧移角的增大而迅速升高。由于循环劣化,混凝土板的Vc/V 曲线随着层间侧移角的增大而迅速降低。层间侧移角达到0.073%时,钢板承担的剪力占比Vs/V 为65.63%,混凝土板承担的剪力占比Vc/V 为34.37%;层间侧移角达到0.22%时,钢板进入剪切屈服阶段,此时钢板承担的剪力占比Vs/V 为95.61%,混凝土板承担的剪力占比Vc/V 为4.39%。钢板进入屈服平台后,钢板承担的剪力占比Vs/V 曲线趋于稳定,基本保持在97.22%左右,混凝土板承担的剪力占比Vc/V 稳定在2.78%左右。

图13 钢板和混凝土板承载比例
由图13(b)可知,N7×7-D22-Ts15-Tc200-OB 中钢板分担的剪力占比Vs/V 和混凝土板分担的剪力占比Vc/V 曲线与图13(a)曲线相似。当层间侧移角为0.073%时,钢板剪力占比为74.54%,混凝土板剪力占比为25.46%;层间侧移角达到0.22%时,钢板发生剪切屈服,钢板剪力占比Vs/V 为95.61%,混凝土板剪力占比Vc/V 为4.39%。钢板剪切屈服后,随着层间侧移角的增大,钢板承担剪力占比Vs/V 以及混凝土板承担剪力占比Vc/V 的变化不再明显,Vs/V 为98.92%左右,Vc/V 稳定在1.08%左右。
2.3 栓钉行(列)合剪力
算例N7×7-D22-Ts15-Tc200 栓钉行(列)各栓钉剪力之和的变化曲线见图14。HSX-i 及HSY-j 分别表示第i 行栓钉的水平剪力之和及第j 列栓钉的竖向剪力之和,变量i 是栓钉行从上至下的序号,变量j 是栓钉列从左至右的序号。栓钉行(列)合剪力沿坐标X 轴与Y 轴正向为正、负方向为负。对比图14(a)及图14(b),HSX 曲线和HSY 曲线具有相似的变化规律。曲线的第一阶段和第二阶段,HSX-1 和HSX-7 行栓钉合剪力明显高于其他行;第三阶段,HSX-3 和HSX-5 处栓钉行合剪力明显高于其他行。第一阶段,HSX-7 栓钉合剪力在层间侧移角-0.15%时达到峰值32.586 kN;HSX-1 和HSX-7 栓钉合剪力在层间侧移角0.22%时达到峰值,分别是43.409、40.564 kN;第三阶段,HSX-3 和HSX-5 栓钉合剪力在层间侧移角2%时分别是36.122、23.634 kN;HSX-5 栓钉合剪力在层间侧移角为-2%时是38.693 kN。
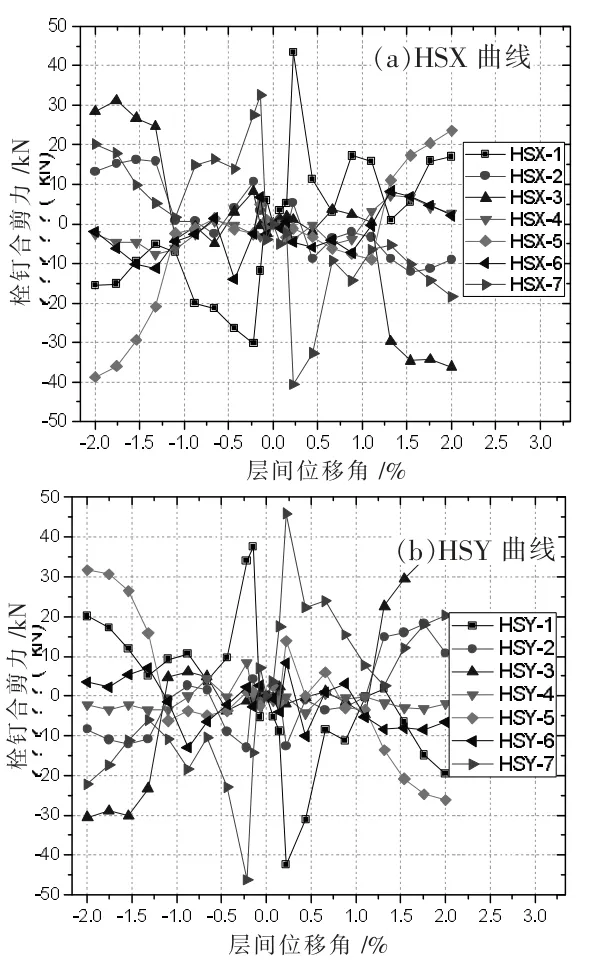
图14 栓钉合剪力发展曲线
在钢板弹性阶段和屈服阶段,栓钉协调钢板和混凝土板的面内变形,混凝土板内的栓钉受到周围混凝土的挤压受剪。在循环荷载作用下,不同位置、不同时刻的单个栓钉受到的混凝土挤压力方向、大小均不相同,栓钉剪力存在波动现象,栓钉行(列)剪力合力也就存在波动现象。但是不同参数的算例,均表现为外围栓钉行(列)剪力合力大于内部栓钉行(列)剪力合力。钢板发生屈曲后,屈曲波形边缘的栓钉受弯,弯曲产生的剪力增大。
N7×7-D22-Ts15-Tc200 单个栓钉剪力分布如图15(a)、(b)、(c)、(d)所示,分别对应层间侧移角为-0.15%、0.22%、2%、-2%之时。图中单个栓钉剪力在X 轴、Y 轴方向的分量用矢量表示,其剪力值大小由矢量长度表示,数值已标注于图中。图中,h 为墙板高度,l 表示墙板宽度。侧移第一阶段,剪力最大的栓钉位于边界行和列,特别是角部栓钉,内部栓钉剪力均较小;侧移第三阶段,钢板发生整体屈曲,位于屈曲波形边缘的栓钉受弯而产生的弯曲剪力增大。

图15 N7×7-D22-Ts15-Tc200 栓钉剪力分布(单位:kN)
2.4 栓钉剪力变化
以N7×7-D22-Ts15-Tc200 为例说明单个栓钉剪力的变化。N7×7-D22-Ts15-Tc200 部分栓钉剪力的发展如图16 所示。HST-i-j 表示位于第i 行第j列的栓钉剪力。变量i 是从上至下的栓钉行序号,变量j 是从左至右的栓钉列序号。
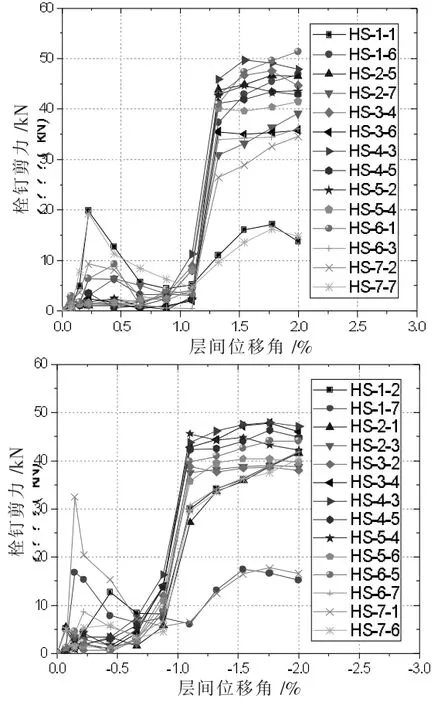
图16 单个栓钉剪力-层间侧移角
从图16 中可以看出,单个栓钉的剪力变化与栓钉行(列)合剪力的变化特征相似。侧移第一阶段,剪力最大的栓钉位于墙板角部,内部栓钉剪力均较小。侧移第三阶段,位于屈曲波形边缘的栓钉弯曲剪力明显超过墙板角部的栓钉,栓钉弯曲产生的剪力在层间侧移角2%时达到最大值。
3 栓钉剪力需求
在循环荷载后期,钢板屈曲后混凝土板破坏严重,如果循环荷载后期允许栓钉进入塑性发生损坏,可按混凝土板达到峰值剪力时对应的栓钉剪力提出栓钉的设计剪力需求。以下主要分析混凝土板达到峰值承载力时对应的栓钉剪力,即栓钉第一个峰值剪力,此剪力为钢板与混凝土板平面内相对变形产生的剪力。不对钢板较大屈曲变形引起的栓钉弯曲剪力进行分析。
本章栓钉剪力需求分析所依据36 个有效算例的混凝土板厚和栓钉间距都满足循环荷载下,钢板进入塑性平台后屈曲,单面外包混凝土C-PSW/CE 在层间侧移2%内承载力劣化均不超过15%。
3.1 影响栓钉剪力的参数
侧移第一阶段,即钢板弹性阶段,此时栓钉的作用是协同钢板和混凝土板在平面内的变形。C-PSW/CE各参数对于第一阶段单个栓钉峰值剪力的影响如图17 所示。

图17 单个栓钉最大剪力与影响因素的关系
图17(a),当混凝土板厚度一定时,单个栓钉最大剪力Vhsm随栓钉间距S 的变化并不呈简单的关系,而是有波动。分析栓钉间距变化的9 个算例,其栓钉剪力值在25 kN 至35 kN 之间,波动不大,且均小于栓钉屈服剪力。说明在本文算例所选取的栓钉间距范围内,栓钉间距对于第一个栓钉剪力峰值的影响较小。
图17(b),当栓钉间距S 为定值时,随着栓钉直径d 的增大,单个栓钉最大剪力Vhsm急剧增大。12 个算例的剪力值在10 kN 至40 kN 之间,变化较大。
图17(c),当其它参数不变时,随着钢板厚度ts的增大,单个栓钉最大剪力Vhsm上升,且增幅较大,说明钢板厚度对于单个栓钉剪力有很大的影响。各算例的剪力值在15 kN 至53.6 kN 之间变化。
图17(d),当其它参数不变时,单个栓钉最大剪力Vhsm随着混凝土板厚度tc的增加呈下降趋势,但下降幅度不大,各算例的剪力值在25 kN 至35 kN 之间。说明,本文算例所选取的混凝土板厚度对于第一阶段栓钉最大剪力的影响较小。
图17(e),墙板高宽比在0.5 至1 之间时,单个栓钉最大剪力Vhsm表现出先降后升的趋势。对墙板高宽比α 为0.5、0.75 和1.0 工况,各算例的栓钉剪力值在25 kN 至47 kN 之间变化。
3.2 栓钉剪力需求
对第一个峰值剪力,单个栓钉剪力与此栓钉所在行水平合剪力同时达到峰值,定义参数α1为单个栓钉最大剪力Vhsm与所在栓钉行水平合剪力峰值Vrm之比;定义参数α2为栓钉行水平合剪力峰值Vrm与混凝土板峰值剪力Vc之比;定义参数α3为混凝土板剪力峰值Vc与钢板屈服剪力Vsy之比;定义参数η 为栓钉间距调整系数。单个栓钉最大剪力Vhsm与钢板屈服剪力的关系如式(1)所示。
α1与栓钉列数nc(栓钉间距S)及墙板高宽比α 关联性较强,将α/nc视为自变量,将有限元结果Vhsm/Vrm视为因变量,通过拟合得到参数α1如式(2)所示。
参数α2与栓钉列数nc(栓钉间距S)、栓钉直径d、混凝土板厚度tc、钢板厚度ts及墙板高宽比α 关联,但关联程度不同。将ncts0.3d0.7/tc视为自变量用于拟合参数α2,见式(3)。
钢板的剪切屈服剪力Vsy取决于钢板厚度ts、钢板宽度l、钢材屈服强度fy,Vsy=0.58tsfyl。参数α3与混凝土板厚度tc、混凝土抗压强度fc及墙板宽度l 相关。因各算例均采用相同的墙板高度,所以混凝土板剪力Vc、钢板剪切屈服剪力Vsy均与墙板的高宽比α 相关联。将αtcfc/(tsfy)视为自变量用于拟合参数α3,见式(4)。
根据式(1)~(4),可得单个栓钉第一峰值剪力Vhsm计算公式(5)。
对于栓钉间距S≤300 mm 的工况,公式(5)中的调整系数η 取值0.8;其它工况η 取值1.0。
36 个有效算例有限元结果及由公式(5)计算的结果列于表2。与有限元结果对比,两者之间存在一定的差异。式(5)可供循环荷载下预估单面外包混凝土C-PSW/CE 栓钉剪力需求(对应第一个峰值剪力)时参考。

表2 式(5)与有限元结果对比
4 结论
(1)C-PSW/CE 在承受水平循环荷载时,其承载能力主要来源于钢墙板。根据钢墙板的状态可将栓钉的受力分为三个阶段。第一:钢板弹性未屈曲,栓钉主要起协同钢板与混凝土板平面内变形的作用,剪力最大的栓钉位于边界行或列,特别是角部栓钉剪力较大,内部栓钉剪力均较小,混凝土板剪力大部分由边界行、列栓钉传递,此阶段混凝土板达到峰值承载力;第二:随着侧移增大,混凝土板劣化严重,承载力快速下降,栓钉剪力减小;第三:钢板在塑性平台段发生屈曲后,位于屈曲波形边缘的栓钉受弯而产生较大弯曲剪力。
(2)单个栓钉的最大剪力Vhsm受栓钉间距S、混凝土板厚tc的影响较小(因控制劣化率,本文有效算例混凝土板均较厚,栓钉间距均较小且变化不大)。当栓钉间距一定时,随着栓钉直径d 或钢板厚度ts的增大,单个栓钉最大剪力Vhsm增大;单个栓钉最大剪力与墙板高宽比关联较大。
(3)公式(5)可供预估强震区单面外包混凝土C-PSW/CE 延性设计时栓钉剪力需求参考。对于高烈度区的单面外包混凝土剪力墙,栓钉间距不应大于500 mm,也不宜小于300 mm;宜采用高厚比λ≤250 的钢板;混凝土板的厚度不应小于200 mm;不适合选用直径过大或过小的栓钉,宜选择16 mm、19 mm、22 mm。
