低信噪比场景下全相位FFT载频估计改进算法

吴呈瑜,张红斌,占 敖

(浙江理工大学 信息科学与工程学院,浙江 杭州 310018)

0 引言

随着通信技术的飞速发展,生活环境中充满着各种无线电波。然而,在现实世界中,这些无线电波常常受到各种干扰和噪声的影响,使得无线通信的可靠性和性能面临着巨大的挑战。其中,调幅(Amplitude Modulation,AM)信号作为一种重要的模拟调制方式,被广泛应用于广播和无线通信领域[1]。它的简单性、鲁棒性以及对频率偏移和相位变化的抗干扰能力使之成为一种理想的选择。然而,在无线电监测[2]和通信信号识别[3-4]等特定场景下,AM信号的接收过程往往遭受到严重的干扰,如噪声、多径衰落和其他无线电设备的干扰等,导致较大的性能损失和信息传输错误。

为了解决低信噪比(Signal-Noise Ratio,SNR)环境下AM信号的载频估计问题,并提高信号的接收质量和解调性能,研究者们展开了广泛的研究工作。在已有的研究中,许多载频估计算法被提出和应用,例如最大似然估计算法[5]、周期图谱算法[6]、能量重心算法[7]等。这些算法在一定程度上改善了低信噪比环境下AM信号的性能,但仍存在一些问题和局限性,如对计算复杂度敏感、对信噪比要求较高、鲁棒性不强等。

使用快速傅里叶变换(Fast Fourier Transform,FFT)进行载频估计也是一种常见的信号处理方法。FFT在载频估计中的优势在于其高速计算和精确性[8]。通过采用FFT算法,可以大幅提高计算效率,特别适用于实时信号处理和高速通信系统。另外,FFT所得到的频谱图显示了信号的频域特性,使得频率估计更加直观和准确。同时,FFT算法还适用于对带噪声信号进行处理,通过去除噪声等预处理步骤,可以得到更精确的载频估计结果[9]。

1 相关工作

文献[10]最早提出了一种基于FFT的全相位FFT(all-phase FFT,apFFT)。文献[11]严格证明了对比传统FFT,apFFT有更好的抑制频谱泄漏特性。文献[12]提出apFFT不需要频率估计即可得到较为精确的相位信息,称为相位不变性。文献[13]则通过模拟不同环境下噪声对apFFT振幅谱和相位谱的影响,证明了apFFT有良好的抗噪声性能。文献[14]利用文献[12]提出的相位不变特性,提出了全相位时移相位差载频估计算法。针对文献[14]遇到的相位模糊问题,文献[15]引入相位压缩运算,将全相位时移相位差载频估计算法做了改进,对相位模糊现象有了较好的优化。

值得注意的是,过去的研究大多集中在普通信噪比条件下进行,而在较低信噪比场景下的研究相对较少。噪声是干扰载频估计准确性的主要因素之一,会增加信号的不确定性,引入额外的频率成分,导致载频估计的误差。噪声与信号混合后,频谱展宽和功率衰减在频域上显现,使得原本清晰的载频信号变得模糊且难以准确估计。此外,当噪声强度较大时,会掩盖或削弱载频信号的显著特征,进而更容易受到频率漂移[16]、多径效应[17]和其他环境因素的干扰。这些情况的发生可能导致载频估计偏差的增大,甚至无法正确估计载频值。

在无线电监测和通信信号识别等特定场景下,经常会遇到噪声较大的情况[18-19],现有方法可能存在一些问题或痛点。例如,apFFT在抗噪声性能方面的优势是否仍然适用于极低信噪比环境;apFFT信号载频估计精度在这种信噪比环境下相较于其他方法是否还有优势;如何改进apFFT算法使得在低信噪比场景下信号载频估计的精度得到提高。对于这些问题,目前的文献中尚未给出明确的答案,因此,进一步的研究和分析是必要的。

本文旨在研究低信噪比环境下AM信号apFFT载频估计算法,提出一种改进的、有效的估计方法,以克服现有方法的不足之处。本文将从理论分析和算法设计两方面展开详细研究,结合仿真实验,验证所提方法的可行性和优越性。

2 apFFT载频估计算法

apFFT是一种频谱分析方法,通过对采样序列进行apFFT变换,可以准确地提取出信号的幅度谱和相位谱。相比传统FFT方法,apFFT具有更好的抑制谱泄漏的性能,可以降低谱间干扰、提高提取载波信息的精度。

当N=4时,apFFT谱分析流程如图1所示,具体而言是取长度为(2N-1)的卷积窗ωc对整体数据进行加权,将除去中间元素x(0)以外,相隔为N的元素互相叠加,从而得到叠加后的数据y(0),y(-1),y(-2),…,y(-N+1),再对数据进行FFT即可得到apFFT的结果Y(k)[13]。

apFFT谱分析流程中的卷积窗通常取对称且长度都为N的前窗f和后窗b相卷积而得到,中心样点为对称点。则:

ωc(n)=f(n)*b(-n),n∈[-N+1,N-1],

(1)

给定一个单频复指数序列信号:

x(n)=A0ej(ω0n+θ0),

(2)

式中:信号的幅值为A0,数字角频率为ω0,初相位为θ0,且ω0=βΔω,频率分辨率Δω=2π/N,k∈[0,N-1]。经过传统加窗FFT和双窗apFFT之后,得到谱分析XN(k)和YN(k)如式(3)所示:

(3)

观察式(3)中两个谱分析结果,双窗apFFT谱分析结果显示带有平方项,这表明在apFFT中对所有谱线进行了平方处理,使得原本突出的主谱线变得更加明显。由此可知apFFT相比于传统的FFT有更好的抑制频谱泄漏效果。

另外通过对比式(3)也可以发现apFFT具有相位不变性的特性:YN(k)谱线上的主谱线相位值不会随着k的改变而改变,假设幅度谱的峰值所在的谱序号为k0,在apFFT中取k0处的相角就可以得到最终apFFT中心样点x(0)的相位值[12]。

在apFFT谱分析的基础上,进一步提出了一种基于全相位时移相位差法的AM信号载频估计算法。该方法利用了apFFT良好的频谱泄漏抑制性能和相位不变性,使用apFFT分析AM信号的幅谱和相谱特性。载波频率估计基于载波频谱线附近两段延迟序列之间的相位差[14]。

具体而言,首先,给定上述的x(n)序列,取n∈[-N+1,N-1],根据apFFT的相位不变性,序列x(n)中心样点x(0)的理论相位值φ′1=θ0。然后,将序列时移n0个单位,则n∈[-N+1-n0,N-1-n0],新序列的中心样点x(-n0)的理论相位值φ′2=θ0-ωcn0,即φ′2=φ′1-ωcn0。结合上述分析,将两个理论相位值做差,就能得到载频估计算法的估计式:

(4)

apFFT谱分析方法被广泛应用于多个领域。除了本文对AM信号进行载频估计的研究外,该方法还在其他调制方式上得到了应用。文献[20]提出了一种基于apFFT的调频激光测距方法,通过采用时移相位差法对频率进行测量,并在Matlab环境下对实验数据进行频率解算和目标距离计算。文献[21]结合apFFT探讨了一种基于多频移键控的车载雷达系统实现方案。这些研究可以进一步提升通信系统的性能,并为实际应用中的信号处理和解调提供更多的选择和改进方向。

3 apFFT均值修正样条插值算法

信噪比用于衡量信号中有用信号与噪声的相对强度,是通过计算信号的功率与噪声功率之比来评估的。信噪比的计算如式(5)所示:

(5)

式中:Ps为信号的功率,Pn为噪声的功率。

低信噪比场景下的多次实验表明,apFFT的载频估计结果经常会出现较大的波动。然而,这些结果中总会有几次预测接近正确值,并且这些结果的相对误差较小。为了应对上述载频估计情况,本文设计了一种基于均值修正样条插值算法来处理apFFT的载频估计结果,并进一步对数据进行校正,算法流程如图2所示。

图2 均值修正样条插值算法流程图Fig.2 Flowchart of the mean-corrected spline interpolation algorithm

将同一信噪比环境下循环累计一定次数的载频估计结果存入一个数组中,然后将数组内所有数据传入均值修正样条插值算法进行处理。插值过滤过程采用两层嵌套的循环来遍历传入数组内的元素,并计算它们之间的差值。如果差值的绝对值小于或等于预先设定的阈值delta,则将这两个数据点添加到临时数组中。总之,这一过程旨在移除数组中差异超过阈值delta的数据点。

均值修正过程是通过对数据集进行统计分析,计算出数据的均值和标准差,然后根据设定的阈值,将超出阈值的数据点视为异常值,并进行修正[22]。均值则表示数据集的平均值,即将所有数据点的总和除以数据点的个数得到。在本文中,使用临时数组temp来存储修正后的数据点。

(6)

标准差是衡量数据离散程度的统计量,标准差的值越大,表示数据的离散程度越高。

(7)

根据设定的阈值、数据点的均值和标准差来判断数据点是否为异常值。若超出阈值则为异常值,将超出阈值范围的数据点替换为数据的均值,实现对异常值的修正。

均值修正法关键之一是确定适当的阈值,过高的阈值可能导致修正后的数据在分散程度上过于紧凑,损失了重要的变化和信息。相反,如果阈值设定过低,则修正后的数据中除均值以外的数据点可能会过少,导致丢失了重要的数据点。均值修正样条插值能够更好地适应异常点,得到的数据能让下一部分插值中获得更平滑地过渡,并且可以减轻在低信噪比环境下导致的频谱泄漏问题,在载频估计中具有较好的抗干扰能力。可以有效地去除异常值,使得数据更加符合正常的分布情况,并且提高数据的准确性和可靠性。

在三次样条插值过程中,首先,根据输入的离散数据点,计算输入的每个相邻数据点之间的差值:

3.2.3 气滞便秘证 主症：大便秘结，欲便不得。兼症：①胸胁痞满；②腹胀疼痛；③嗳气频作。舌脉指纹：①舌质红；②苔薄白；③脉弦，指纹滞。

h(i)=x(i+1)-x(i),

(8)

以及它的参数:

(9)

然后,对于每个子区间,求解三次多项式S(x),通过以下方程确定多项式系数:

S″[x(i)]=0。

(10)

确定多项式在相邻数据点处的导数匹配条件:

h(i)·S″[x(i)]+2*[h(i)+h(i+1)]·S″[x(i+1)]+
h(i+1)·S″[x(i+2)]=3delta(i+1)。

(11)

该过程是针对i=0,1,…,n-2进行的,其中n是数据点的总数。

最后,根据求解得到的每个子区间的三次多项式S(x),在新输入点xx上进行插值计算,得到插值结果yy,将三次样条插值得到的曲线计算均值,得到最终的均值修正样条插值算法在低信噪比环境下信号载频估计结果[23-24]。

样条插值通过使用分段低阶多项式来逼近数据,产生平滑的曲线或曲面。与牛顿插值的高次插值多项式相比,样条插值能够减少龙格现象和振荡现象,从而得到更加平滑的拟合结果[25]。此外,样条插值具有灵活的控制节点特性,可以根据实际情况选择和调整节点密度,以适应不同程度的数据变化,提高插值结果的适应性和精度。

在载频估计问题中,数据的平稳性要求较高,因此样条插值是一种合理且有效的选择。通过使用样条插值方法,能够更准确地反映数据的变化趋势,避免过拟合和欠拟合问题的影响。同时,样条插值保持曲线的光滑性,有助于提取数据中的潜在规律和趋势。

4 仿真实验

为了验证在低信噪比环境下,基于apFFT的均值修正样条插值结合的AM载频估计算法的效果,设计了仿真实验。使用Matlab信号处理库模拟了低信噪比环境。通过在原始信号中添加高斯噪声,调整了信噪比的水平来模拟不同的信号质量;并分别采用原始FFT载频估计算法、apFFT载频估计算法以及改进后添加均值修正样条插值算法的apFFT载频估计算法进行对应环境下的载频估计,最终将得到的估计结果进行对比和分析。

用Matlab生成载波频率为1 000 Hz,采样率fs为384 000 Hz,载波幅度为1,调制幅度为0.5的AM信号,添加信噪比为-44～-29 dB的高斯噪声,并加入一段幅度为0.1,频率为2 000 Hz的正弦干扰信号,取N=8 192×10、移位量n0=96,分别模拟了信噪比较低时不带干扰和带有正弦干扰的实验环境。生成的基带信号xm(t)时域波形、载波信号xc(t)时域波形、AM信号x(t)时域波形如图3所示。移位前后的幅度谱和相位谱如图4与图5所示。

(a) 基带信号波形

(b) 载波信号波形

(c) AM信号波形图3 基带信号、载波信号和AM信号波形Fig.3 Baseband signal,carrier signal,and AM signal waveforms

(a) 移位前幅度谱

(b) 移位后幅度谱图4 信号幅度谱图Fig.4 Signal amplitude spectrogram

(a) 移位前相位谱

(b) 移位后相位谱图5 信号相位谱图Fig.5 Signal phase spectrogram

根据式(4)得到载频估计的数字角频率的值,可以得到载频估计的模拟频率:

(12)

将调制得到的AM信号中添加信噪比为-44～-29 dB的高斯噪声,分别采用上述三种不同的载频估计方法进行仿真实验。其中前两种方法(原始FFT载频估计法和apFFT载频估计法)在每个信噪比环境下循环估计3 000次,取平均值得到最终估计结果,第三种方法是将循环估计3 000次得到的数据进行均值修正样条插值算法处理后,得到最后的估计结果。将三组结果数据与原始载频对比计算误差,有无干扰环境下得到的仿真结果分别如图6与图7所示。

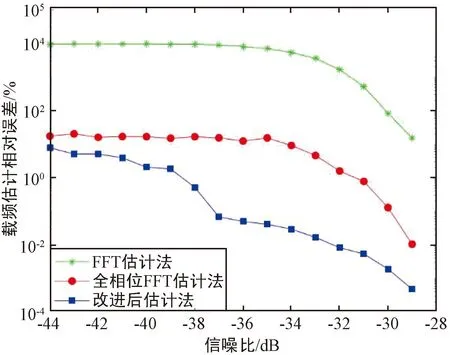
图6 无干扰改进前后误差对比Fig.6 Comparison of errors before and after interference-free improvement

图7 存在干扰改进前后误差对比Fig.7 Comparison of errors before and after improvement in the presence of interference

由图6与图7可知,随着信噪比的增加,三种方法均显示相对误差稳步下降,加入的正弦干扰使载频估计误差稍有增大,但总体影响不大,说明本文载频估计算法有较好的抗干扰效果。另外改进后的算法载频估计效果始终优于另外两种方法,在信噪比低于-30 dB的情况下相对误差还可以达到10-3数量级。与其他两种方法相比,本文提出的AM信号载频估计均值修正样条插值法在信噪比为-35～-30 dB表现最佳。

根据上述分析,选定仿真信噪比为-34 dB,并加入正弦干扰信号,为了能更直观地展示均值修正样条插值法的效果,在当前信噪比环境下共估计75次,如图8所示,在图中标记出了这75个载频估计结果点,并分别生成了散点图。

图8 存在干扰原始载频估计结果分布Fig.8 Distribution of original carrier frequency estimation results in the presence of interference

由图8可以看出,当处于信噪比较低的环境时,apFFT载频估计法得到的估计结果容易发生较大的波动,但是大部分预测结果还是能较为准确地落在正确载频值附近,然后经过差值过滤过程,阈值设置为1.5,结果如图9所示。可以观察到,估计误差较大的结果都已经被滤除,接着将得到的结果进行均值修正过程,设定方差范围阈值为0.5,仿真结果如图10所示。

图9 存在干扰差值过滤后载频估计结果分布Fig.9 Distribution of carrier frequency estimates after filtering in the presence of interference differences

图10 存在干扰均值修正后载频估计结果分布Fig.10 Distribution of carrier frequency estimates after mean correction for presence of interference

为了展示在本次实验中样条插值方法相对于其他插值方法的优越性,在仿真实验中引入了牛顿插值,并将其插值得到的曲线与样条插值结果进行比较。图11展示了不同插值方法载频估计相对误差对比。

图11 不同插值方法相对误差对比Fig.11 Comparison of relative errors of different interpolation methods

由于牛顿插值拟合的曲线在两端出现了龙格现象,导致曲线在首末段出现振荡,载频估计结果误差也因此增长。由图11可知,样条插值法的载频估计误差远小于牛顿插值算法得到的载频估计误差。样条插值方法使用分段低阶多项式逼近数据,有效地减少了振荡现象。经过样条插值,将一些离散的点拟合成一条连续的曲线,再取曲线均值就可以得到最后的载频估计结果。

综上所述,均值修正样条插值算法可以有效提高低信噪比环境下AM信号载频估计的精度,且进行的迭代次数越高,估计的结果也会越准确,但同时算法复杂度也会呈平方式增长。因此,在实际应用中需要根据需求平衡算法的精度和运行效率。

5 结束语

本文对apFFT载频估计方法进行一般性的分析与讨论,针对在低信噪比环境下apFFT载频估计结果容易发生较大波动的问题,利用均值修正样条插值的算法对相同低信噪比下apFFT载频估计得到的不同结果进行数据校正,有效提高了低信噪比环境下载频估计结果的准确率,较原始方法有了3～5 dB的提升。在信噪比低于-30 dB的情况下相对误差可以达到10-3数量级,并对比了存在干扰信号与不存在干扰信号环境的载频估计结果。结果表明所提出的方法有较强的抗干扰能力,在特定实验环境下有较高的实用价值。在未来的工作中,可以进一步研究apFFT在不同调制方式上的应用,以拓展该方法在不同调制方式下的适用性和性能表现。这项研究可以作为之后的研究内容参考,为实际应用中的信号处理和解调提供更多的选择和改进方向。