基于改进D*Lite的二维路径连续动态规划算法
2023-12-15刘书勇韩新宇
傅 亮,刘 峰,刘书勇*,韩新宇
(1.中国航空无线电电子研究所 民机航电系统部,上海 200241;2.哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨 150001)
0 引言
路径规划[1]是让目标对象基于环境模型下寻找一条经过起止节点的无碰撞障碍物的安全路线优化问题,它广泛应用于移动机器人、空中无人机、自动驾驶车辆、水面无人艇等领域[2-8]。基于规划模式可划分为静态路径规划与动态路径规划两大类。静态路径规划常用算法有图搜索算法[9-11]和智能优化算法。图搜索算法如Dijkstra、A*、RRT等,智能优化算法如蚁群算法、遗传算法、粒子群算法、蝙蝠算法等[12-15]。静态路径规划算法实施要求之一是需要全区域的地形信息,对未知地形则不具备规划能力。为解决在未知领域进行路线搜索的问题,提出了动态路径规划算法,如D*、LPA*、D*Lite等[16-18]。
D*Lite算法是融合D*和LPA*提出的一种反向搜索的动态路径规划算法,应用在未知环境下进行快速路线搜索,可以对未知突变障碍进行重规划,是一种高效的规划算法,但是它依然存在易受运动物体影响及路径贴近障碍物等问题,因此众多研究学者对其进行了改进。吴涛等人[19]引入跳点搜索概念,仅对跳点进行访问,能够有效优化路径长度。杜轩等人[20]结合人工势场(Artificial Potential Field,APF)法对D*Lite规划路线进行重规划,使得目标物体在移动中能够与障碍物保持有效的安全距离,但本身并未对D*Lite算法进行改进。张毅等人[21]针对原有Boustrophedon单元分解法进行改进重构,提取关键单元,引导正确搜索方向,有效提高规划速度。戴年慧等人[22]进入安全系数阻止危险节点作为路径优先选择节点以避免斜穿过障碍,导致冗余点过多。以上改进算法仅对预规划路径进行单次动态重构,并没有进行多次重构优化,没有体现动态规划的多样性。
针对以上问题,本文提出了一种改进D*Lite的二维路径连续动态规划算法(Continuous D*Lite,CD*Lite)。本文算法基于栅格法进行环境建模,记n·m矩阵。优化原始D*Lite算法的切比雪夫启发估计函数,使其在估计数值上更加贴近实际路线规划。引入人工势场的引力场概念,作为补充启发估计函数,并提出了一种全域启发估计算子。引入人工势场的斥力场概念,提出了一种方向禁忌矩阵,能够避免斜穿栅格障碍节点。优化重规划模式,使其能够在连续产生动态障碍的条件下对路径进行持续重构。最后引入冗余点删除机制,使得规划路线更加平滑。
1 相关工作
1.1 D*Lite算法
D*Lite[18]是由Sven Koenig和Maxim Likhachev于2002年提出的一种基于LPA*和D*的动态路径规划算法。LPA*是一种基于A*和Dynamic SWSF-FP思想的正向传播增量式动态路径规划算法,但正向搜索会因为很多分支导致效率下降,因此D*Lite融入D*的逆向搜索思想,从目标节点反向搜索起始节点,能够有效地减少节点访问次数,减少搜索时间。D*Lite是一种起始节点可变化的反向规划算法,因此更适合应用于未知环境或预规划路线突变障碍的情况。
D*Lite算法通过不断更新节点值执行路径搜索过程,其定义如式(1)所示:
(1)
式中:keys是由k1和k2组成的二维矩阵,表示为s节点的键值;sstart为当前开始节点,sgoal为目标节点,slast为重构路径之前的sstart节点,g(s)为sgoal节点到s节点的历史最小实际代价值;rhs(s)为sgoal节点到s节点的启发估计值;km为键值修饰器,是slast节点到sstart节点的实际移动距离。
D*Lite与LPA*最大的不同在于key值定义,通过引入km因子修饰key,使得启发估计值的sstart节点是可变化的,可以减少不必要节点的计算操作,从而大大提高算法效率,也使得key值比较对于实际而言更有意义。由式(1)可知k1由最小实际代价值、启发估计值、键值修饰器累和求得,其具体定义如式(2)~(5)所示:
(2)
(3)
h(s,sstart)=λ·max(|xs-xsstart|,|ys-ysstart|),
(4)
(5)
式中:Succ(s)为s节点的后继节点集合;λ为单步移动代价;c(s,s′)为边缘实际代价函数,即s节点到边缘s′节点的欧氏距离,xsysxs′ys′为s,s′的横纵坐标值;h(s,sstart)为s,sstart的切比雪夫距离,xsysxsstartysstart为s,sstart的横纵坐标;
算法核心在于不断遍历节点并计算keys放入待检测队列(Priority Queue)。同时由式(2)~(3)可知,g(s)和rhs(s)定义相同,但区别为g(s)为历史最小值、rhs(s)为当前计算值,取二者最小值用于更新keys,共计3种不确定状态如下所示:
① 若rhs(s)=g(s),局部一致状态。此状态表示结点s处于预估与实际基本没有差错的稳定状态。如无外界影响,将一直保持此状态。
② 若rhs(s) ③ 若rhs(s)>g(s),则处于局部欠一致状态。此状态表示节点s周围节点发生障碍物突变导致旧有解失效,已经收到了附近新障碍物直接或间接的影响,因此需要将其放入优先队列中进行进一步判断。 D*Lite算法主要功能包括预规划路径和动态规划路径,具体如下所示: ① 预规划路径:算法初期会通过更新全局地图信息,根据式(1)计算相应扩散节点的keys,并将其置于优先队列中,然后计算优先队列最小keys,计算规则为先按照k1升序排序,再按照k2升序排序,最后优先队列中首项即为所求,更新该s节点的最小实际代价值,根据3种局部状态执行相应操作,遍历边缘节点寻找最优keys作为其前继节点,重复以上操作,直到遍历到sstart节点,功能结束。 ② 动态规划路径:当预规划路径的节点突变为障碍物,会重新计算突变节点的keys,将受到突变节点影响的所有边缘节点全部置于优先队列中,再执行预规划路径功能,完成单次动态路径规划。 人工势场算法是路径规划和局部避障运动中较为常用的方法,该算法的基本思想是在移动点和障碍物周围定义势场,移动点的运动依靠势场力进行驱动。人工势场[23]是由Khatib于1986年提出的一种虚拟力场,它将目标与障碍物看作产生引力与斥力的物体,对其投入场内物体使其沿着场内合力方向进行移动。主要方法为建立引力场Uatt(q)和斥力场Urep(q),如式(6)~(7)所示: (6) (7) 式中:ξ为引力尺度因子,η为斥力尺度因子;ρ(q,qgoal)为物体与目标的欧氏距离,ρ(q,qobs)为物体与障碍物的欧氏距离,ρ0为障碍物的影响半径。 Uatt(q)和Urep(q)的负梯度方向即为引力和斥力的方向,负梯度值即为物体受到引力和斥力的值,如式(8)~(9)所示: (8) (9) 式中:ξ为引力尺度因子,η为斥力尺度因子,ρ(q,qgoal)为物体与目标的欧氏距离,ρ(q,qobs)为物体与障碍物的欧氏距离,ρ0为障碍物的影响半径。 在进行动态路径规划时,针对移动点当前位置附近的节点,使用传统的D*Lite算法来估计启发式值。具体而言,使用切比雪夫距离作为计算方式,该距离是在向量空间中测量两个点之间的一种方法,它定义为两个点在各个坐标上数值差的绝对值中的最大值。切比雪夫距离也被称为棋盘距离,因为它类似于在棋盘上移动棋子的最短步数。在设定的场景中,目标节点周围的邻接节点与目标节点的切比雪夫距离都是1,这意味着在横向、纵向和斜向移动时,到达邻接节点的代价是相同的。然而,在实际情况中,当目标节点向预定节点移动时,“斜走”“先直走再横走”到达预定节点的代价是不同的。因此,需要改进传统启发估计算子以匹配实际路径规划的路径代价,基于式(10)~(12)对其进行改进。 h′(s,sstart)=λ1·diffmin+λ2·(diffmax-diffmin), (10) 式中: diffmin=min(|xs-xsstart|,|ys-ysstart|), (11) diffmax=max(|xs-xsstart|,|ys-ysstart|), (12) 2.2.1 引入人工势场引力算子 人工势场法定义目标点引力场如式(6)所示,引力场引导移动点向目标点运动,在移动点和目标点间无障碍的理想条件下,移动点和目标点坐标间连线距离始终为最短距离;算法不需要对全局轨迹进行搜索,规划时间短、效率高,满足实时和轨迹生成安全性的要求。定义hatt(s)为移动点与目标点的启发估计代价如式(13)所示,即引入人工势场引力算子作为补充启发代价算子。 (13) 式中:ξ为引力尺度因子,xsysxsgoalysgoal为s,sgoal的横纵坐标。 2.2.2 全域启发估计算子 D*Lite算法的启发估计算子如式(1)所示,通过计算起始点到目标点的代价值标识移动点的启发效果,在局部规划中是一种盲目性的试错路径规划,在复杂环境中带来更多的时间效率损耗。为改进keys键值算子,本文提出全域启发估计算子hwhole替换h(s,sstart),如式(14)~(15)所示: (14) 其中: hwhole=h′(s,sstart)+hatt(s), (15) 式中:g(s)和rhs(s)定义如式(2)~(3)所示,h′(s,sstart)和hatt(s)定义如式(10)和式(13)所示。 式(1)中h(s,sstart)为s,sstart的切比雪夫距离,由2.1节可知hwhole内h′(s,sstart)算子改进h(s,sstart)算子的实际路径规划路径代价,提升规划路径精度;由2.2.1节可知,hwhole内新增的hatt(s)算子引导移动点始终向目标点方向移动,不必通过分别计算邻域8个方向的结果后做方向选择,加快算法收敛速度。 D*Lite算法在规划路径时会出现斜穿障碍物顶点的危险行为[22],在实际路径规划当中这种路线会对移动物体产生威胁,需要将其修正为安全行为,如图1所示。 图1 修正危险路线Fig.1 Correct the dangerous route 修正规划路径中的危险路径需要识别危险节点,即障碍物节点。遍历环境内每一格栅格,判定识别其是否为障碍物;同时对其邻接8个方向栅格节点的路线选择和变更情况按照图1的禁忌准则进行确认,并构建邻域方向禁忌矩阵d用于存储危险路线修正变更结果;移动点根据所在节点8邻域的规划路线修正结果,减少重复计算,避免迂回搜索。 邻域方向禁忌矩阵d定义如式(16)所示,在对目标节点进行邻域搜索时,基于其过滤危险节点。 (16) (17) (18) i=x×m+y, (19) 式中:move(i)为i节点能够经过的安全邻域节点;d为p+1行8列的二维矩阵,p对应n行m列栅格模型环境矩阵c内最后一个序号节点;方向禁忌矩阵d的行序号i与n×m栅格模型环境矩阵c内(x,y)节点对应关系如式(19)所示。禁忌矩阵d有8列,即8个分量对应节点8个邻域方向移动有效位,对应邻域节点的标识如图2所示。 图2 邻域节点的标识Fig.2 Identification of neighborhood node 在算法进行邻域节点搜索或动态路径重规划寻找周围影响节点后,基于d进行安全行为判断。从i~j节点寻找到一条路线,如果dij=-1说明j节点不存在,该路线无效;dij=1说明i节点可以移动到j节点,是一种安全行为;dij=0说明i节点不可以移动到j节点,是一种危险行为。dij初始化策略伪代码如算法1所示。 算法1 UpdateD算法1 Input:S2Output:d3BEGIN:4 for eachs∈S5 if s is not existent ∥节点s为无效节点6 dij=-17 ∥ i~j节点的路线为安全路线8 else ifi do not cross j obliquely9 dij=110 elsedij=011 end if12 end for13 returnd ∥更新方向禁忌矩阵14END D*Lite算法由一次全局预规划和一次动态路径规划组成。算法首先执行预规划机制,生成全局初始路线;接着进行动态路径规划,如果全局初始路线上出现突变障碍,会重新设定sstart起点直到新规划路线再次经过sgoal节点,完成一次动态重构路径,目标点会按照更新路线进行移动。如果目标点在完成D*Lite算法更新后的路线上移动时,在snow识别出新的突变障碍,重新使用D*Lite算法规划路线,会导致运算效率降低。本文改进D*Lite算法的动态路径规划过程,提出连续障碍突变动态路径规划算法,即在一次动态路径规划完成后,若识别出新的突变障碍,可继续开展动态路径规划,省略全局预规划过程,大幅提升运算效率。算法输入包括栅格节点集合以及经UpdateD算法输出的方向禁忌矩阵d。输出一个满足上述约束符合既定需求的动态规划局部路线节点集合E,伪代码如算法2所示。 算法2 连续障碍突变动态路径规划算法1 Input:S,d2Output:动态规划局部路线节点集合E3BEGIN:4 ∥既定路线有突变障碍5 If any obstacle changed near s do6 Update sstart and sgoal7 ∥更新全域8 Scan Global Grid and Update snow9 ∥动态规划路线10 Compute shortest path and Update E11 end if12 returnE13END 经过动态规划后,路径从起始节点sstart开始顺序连接邻域节点sgoal,直至到达终止节点,如图3所示的“规划路线”。规划路径中的节点与其相邻节点符合邻域8方向机制,即只能与其周围8个方向中的某一个节点相连。然而,这样的连接方式可能会导致节点冗余的问题。为解决这一问题,本文提出了冗余点删除机制。具体操作是从起始节点开始按顺序遍历路径上的节点,构建一个“过渡路线”,如图3所示。如果这个“过渡路线”不被认为是“危险路线”,则删除当前节点之前的节点。如果被认为是“危险路线”,则返回前一个节点,将其所在的“过渡路线”定义为“最终路线”,并将该节点作为新的起始节点,继续遍历和重复进行冗余点删除,直到达到终止节点。这样构建出的“最终路线”即为经过冗余点删除后优化的规划路径,实现了路径的平滑化,并且目标点移动的方向不再局限于邻域8方向。 图3 冗余点删除流程Fig.3 Redundant point deletion process 本文CD*Lite算法具体实现步骤如下: 步骤1:初始化参数包括rows、cols、snow、sstart、slast、sgoal、km、U、d; 步骤2:执行预规划路径功能,令rhs(sgoal)=0,根据式(14)计算keysgoal,将sgoal和keysgoal作为子项插入U; 步骤3:反向搜索,遍历s节点,根据g(s)和rhs(s)三种不一致状态计算keys并对g(s)和rhs(s)进行同步更新,找到相应代价最小的邻域节点,基于方向禁忌矩阵d筛除危险节点,直到遍历经过sstart且U中子项最小的keys不小于keysstart时规划结束,此阶段延续采用D*Lite算法构建路径方式。 步骤4:执行本文提出的连续动态规划模式,默认目标单次移动单位栅格距离,在移动过程中实时检测突变障碍,若有异常则及时更新方向禁忌矩阵d,更新所有因突变障碍而受到影响的所有节点rhs(s)并执行步骤2和步骤3同类操作,至此完成单次动态路径重构。之后继续实时检测全域既定路线是否有突变障碍,重复以上流程以实现连续动态路径规划,直至目标移动到sgoal,返回全局规划路线与突变障碍节点。 步骤5:最后采用冗余点删除机制对CD*Lite规划的路径进行优化,保留最优路线,算法结束。 基于以上步骤,本文CD*Lite算法伪代码如算法3所示。 算法3 CD*Lite算法1 Input:S,d2Output:全局规划路线节点集合Ewhole3BEGIN:4procedure Initialize()5 initialize s∈S,snow=sstart=slast,U=∅,km=0,d=0,rhs(s)=g(s)=∞,rhs(sgoal)=0;6 Calculate sgoals key and insert into U(sgoal,key)7procedure Calculate Key(s)8 return[min(g(s),rhs(s))+hwhole(s)+km, min(g(s),rhs(s))]9procedure Compute Shortest Path()10 while U.TopKey 本实验的硬件环境:CPU为Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz 12线程;软件环境:Windows 10平台PyCharm 2021.3.3。CD*Lite算法在栅格地图上进行动态路径规划结果验证。实验采用20×20、50×50、100×100三种规模栅格地图,地图内黑色方块为障碍地图块,白色方块为目标可行动区域图块,黄色方块为目标行动终止节点。为保证栅格地图内容随机性,使用随机算法对应生成三种地图节点集,如式 (20)~(21)所示: ob=random.sample(range(0,a·b),c), (20) (21) 式中:ob为障碍节点集,a和b为生成栅格地图的行高和列宽,c为障碍节点数目总和,fieldij为栅格地图节点集。按照实验环境要求生成三种规模地图节点集,为确保生成地图普适性,设置障碍占比分别为 25.5%、40.16%、39.71%,如图4所示。 (a) 20×20栅 (b) 50×50栅 (c) 100×100栅图4 三种规模栅格地图模型Fig.4 Three scale grid map models 在预规划模式中,本文CD*Lite算法将与传统路径规划算法LPA*、D*Lite进行实验对比,参数设定单步移动代价如表1所示。在动态规划模式中,首先基于单次动态规划,本文改进的CD*Lite算法将与文献[22]提出的改进D*Lite算法从路线节点个数、路线长度、运行时间进行对比。然后,进行连续动态规划以验证本文改进的CD*Lite算法。 表1 单步移动代价Tab.1 Single step moving cost 预规划实验结果如图5~图7所示,分别为20×20、50×50、100×100三种规模下各算法所规划的路径,障碍占比分别为 25.5%、40.16%、39.71%,改进效果对比如表2所示。 (a) LPA*20×20 (b) D*Lite20×20 (c) CD*Lite20×20图5 三种算法在20×20规模下的预规划路径结果Fig.5 Three algorithms pre planning path results under 20×20 scales (a) LPA*50×50 (b) D*Lite50×50 (c) CD*Lite50×50图6 三种算法在50×50规模下的预规划路径结果Fig.6 Three algorithms pre planning path results under 50×50 scales (a) LPA*100×100 (b) D*Lite100×100 (c) CD*Lite100×100图7 三种算法在100×100规模下的预规划路径结果Fig.7 Three algorithms pre planning path results under 100×100 scales 表2 CD*Lite与LPA*、D*Lite实验结果数据对比Tab.2 Comparison of experimental results of CD*Lite in this paper,LPA* and D*Lite presented CD*Lite算法在预规划模式下不执行冗余点删除机制,在20×20、50×50和100×100的地图中都能够消除斜穿障碍边界点的危险行为。而传统算法LPA*和D*Lite在路径规划时以最短距离为前提,不考虑实际障碍物的影响,因此会产生较多的危险节点。本文算法通过引入方向紧急矩阵实现了目前的效果。 相比于LPA*和D*Lite算法,改进的CD*Lite算法计算节点代价的次数减少约50%和30%,计算时间减少约50%和35%。这是因为本文提出的全域启发算子能够更好地估计当前节点的代价值,从而更有效地指导算法进行全局路径规划。 改进后的CD*Lite算法考虑到实际应用中需要保持距离,因此在危险节点处需要增加拐点。即使在20×20和50×50的地图中,改进后的算法仍能够保持距离不增加。随着地图规模的增大,与LPA*和D*Lite算法相比,距离仅增加约10%。 动态规划定义为在预规划路径基础上出现突变障碍之后继续路径规划操作,根据实现模式可以分为单次动态规划与连续动态规划。单次动态规划如D*Lite,而本文所提出的CD*Lite可以连续进行单次动态规划即连续动态规划。理论上可以连续进行无穷次动态规划,为便于实验结果解析,本文设计的CD*Lite算法基于上述中的20×20规模栅图选取连续3次动态规划结果如图8所示。图中黄色为移动目标搜索起点,红色为突变障碍节点。移动目标不断更新snow,同时侦查全域既定路线上是否有突变障碍,当运动到图8(b)黄色节点时侦测到异常变化,初始化sstart=snow,slast=sstart并对既定路线进行重构,目标沿新路线移动并更新snow,重复以上步骤的具体路线重构结果如图8(c)~(d)所示。 (a) 真实预规划路线 (b) 突变1 (c) 突变2 (d) 突变3图8 CD*Lite算法连续3次对突变障碍动态路径规划Fig.8 CD*Lite algorithm performs dynamic path planning for abrupt obstacle nodes for three consecutive times 文献[22]提出一种改进D*Lite算法,通过引入安全系数,使得危险节点将不作为路径的优先选择,能够有效地避免斜穿过障碍物栅格顶点。本文将从路径长度、规划曲线拐点个数、运行时间三方面进行对比以验证CD*Lite的连续动态规划模式的可行性,其具体实验结果如表3所示。 表3 CD*Lite与LPA*、D*Lite实验结果数据对比Tab.3 Comparison of experimental results and data between CD*Lite and LPA*,D*Lite CD*Lite算法和文献[22]在进行首次动态路径规划时的操作相同,都需要对所有相关节点keys进行初始赋值。然而,CD*Lite算法与文献[22]的不同之处在于CD*Lite会保留节点信息并进行持续更新。 在持续既定路线节点变异3次后,文献[22]算法没有记忆能力,而CD*Lite算法相比文献[22]算法的节点代价计算次数减少约80%,运算时间减少约70%。这表明本文CD*Lite算法在面对连续既定路线突变障碍情况下能够高效地动态重构路径,展现了其可行性和高效性。 本文融入人工势场的引力场思想提出了一种适用于连续既定路线突变障碍情况下的连续动态路径规划CD*Lite算法,对原始切比雪夫代价估计函数进行改进区分行走代价,使其更贴近真实仿真。引入引力算子提出了一种全域代价估计算子并改进键值算子,能够有效地对当前规划路线的节点进行有效评估,提高了算法规划效率。提出邻域方向禁忌矩阵,有效避免产生危险路线行为;引入冗余点删除机制,使得规划路径更加平滑,使目标移动更加灵活;分别基于预规划和连续动态规划模式下,对模拟栅格地图进行路径规划进行仿真验证,成功验证了本文CD*Lite算法连续动态路径规划模式的优势。1.2 人工势场
2 CD*Lite改进算法
2.1 改进启发估计算子

2.2 改进Key键值算子
2.3 引入方向禁忌矩阵
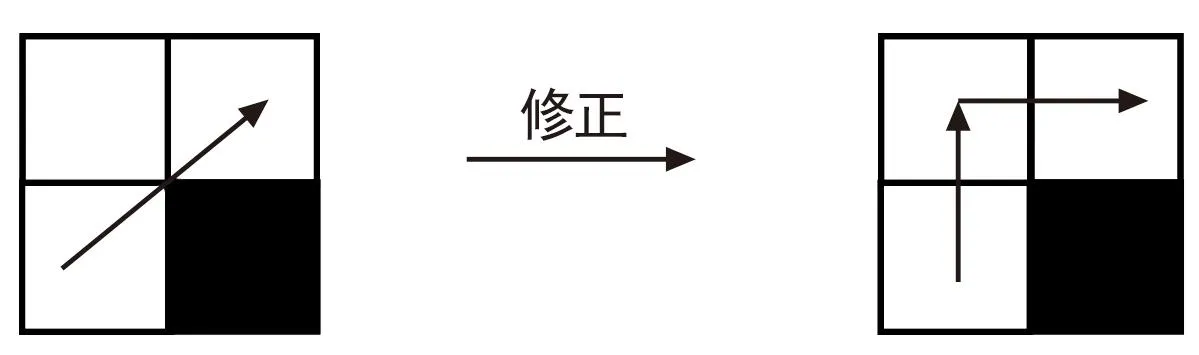
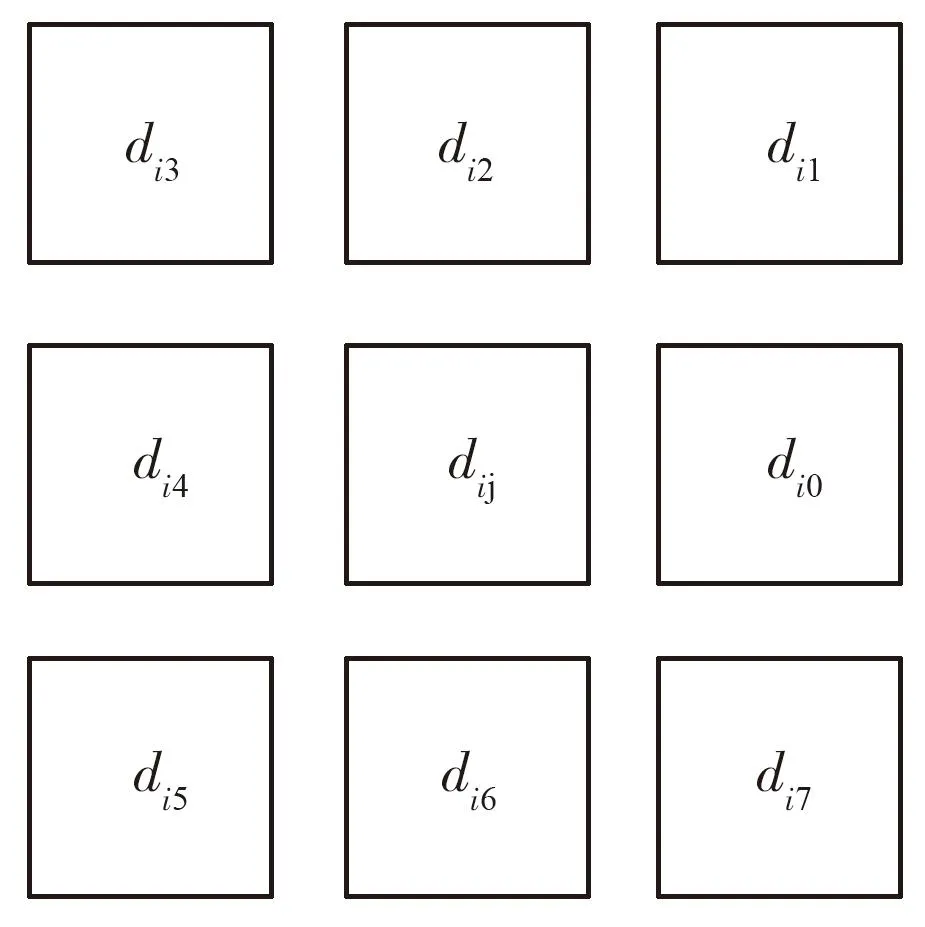

2.4 连续动态规划模式

2.5 冗余点删除机制

3 CD*Lite算法实现

4 实验分析
4.1 实验环境与参数设定




4.2 预规划实验结果分析
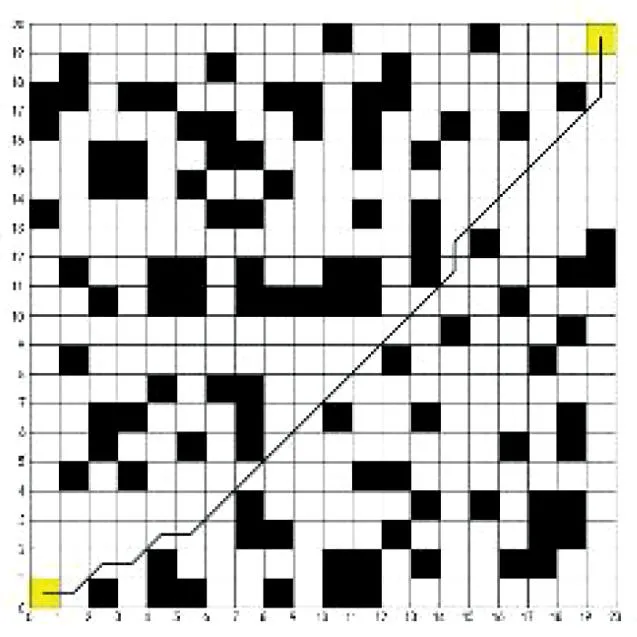











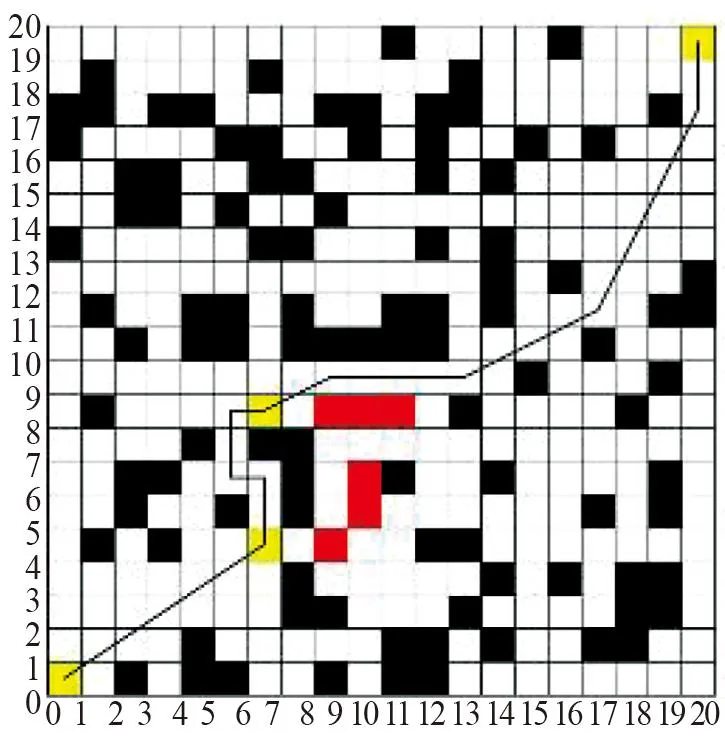



5 结束语
