制造商分担创新产品回收成本的闭环供应链微分博弈

□刘 浪 刘振威 陈 烁

[1. 华东交通大学 南昌 330013；2. 浙江工商职业技术学院 宁波 315012]

引言

创新耐用产品对顾客来说具有“毒性”，顾客很难具有“免疫力”。其扩散规律与病毒传播规律一样，Bass根据病毒传播模型，提出了创新产品扩散模型，这就是著名的Bass模型[1]。苹果手机（iPhone）每款新产品的扩散，都符合这个传播规律。根据苹果公司历年发布的数据，iPhone的销量从2008年的1 162.7万台，增加到2018年的21 772.2万台。根据第三方机构统计，2021年iPhone的销量达到了24 200万台。随着智能手机、电脑和其他智能设备等创新产品市场的不断增大，这些创新产品每年报废量也不断增多，废旧产品回收再制造比传统制造消耗更少的原材料和能源，从而减少资源浪费和碳排放。因此对这些创新产品进行回收再制造对实现“双碳”目标显得尤为重要。特别是第三方回收作为一种专业且高效的回收渠道，能够有效提高产品回收率[2～3]。回收成本分担作为提高回收水平的重要途径[4～5]，能提高对创新产品的回收效率，降低对资源的浪费和对环境的污染，引起学者们的关注和重视。另外，制造商、零售商和回收商之间的生产、再制造、销售和回收是一个长期的微分博弈过程，这已成为供应链领域中一个新的研究热点。

闭环供应链最早起源于单一回收渠道的研究[6～9]。文献[6]最早提出的三个经典的闭环供应链模型，分别为制造商回收、零售商回收和第三方回收。文献[7]在上述三种回收模式的基础上，探讨了在双重销售渠道竞争中，厂商的逆向渠道选择及协同机制的设计。文献[8]则在限额交易制度下，针对上述三种回收模式，将有再制造和没有再制造的情形进行了对比。文献[9]研究了电商平台主导的闭环供应链，分别研究了集中回收、制造商回收、零售商回收、第三方回收等四种单一回收模式。在文献[6]提出的经典模型基础上，许多学者们对第三方回收的情况展开了大量的研究[10～14]。如文献[10]研究了由第三方回收废旧电子电气产品的闭环供应链。文献[11]考虑政府补贴和规模效应，研究了第三方回收的闭环供应链。文献[12]在闭环供应链成员公平关切的情形下研究了各成员及整个系统的最优定价决策与协调策略。文献[13]对产品性能和环境影响的两种偏好构建了不同销售渠道的闭环供应链模型，并探讨了双重偏好对上述渠道差异的影响。文献[14]研究了由制造商和第三方回收商组成的双边平台。随后，有学者开始研究有两个回收渠道的闭环供应链[15～16]。如文献[15]研究了零售商和第三方回收商回收竞争的闭环供应链。文献[16]研究了由两家主导的原始设备制造商（Original Equipment Manufactures, OEMs）和两家第三方再制造商（Third-Party Remanufactures, TPRs）组成的竞争性闭环供应链。

上述研究都假设闭环供应链各成员的决策是不随时间变化的、静态的，而随着信息化时代的到来和网络的普及，信息传递越来越迅速，供应链对市场变化的反应也越来越迅捷，供应链各成员的决策将可以实时变动，此时其静态决策假设将不再适用。近年来有众多学者投入到动态闭环供应链的研究中。如文献[17]较早研究由零售商回收的闭环供应链微分博弈模型。大多数研究都集中在由一个制造商和一个零售商组成的两级闭环供应链[18～23]，文献[18]研究了由一个制造商和一个零售商组成的闭环供应链。文献[19]在闭环供应链中考虑了零售商分担制造商回收成本。文献[20]研究了制造商和零售商都投资产品回收的闭环供应链。文献[21]考虑了回收率的随机扰动对二级闭环供应链的影响。文献[22]研究了不同权力结构对二级闭环供应链的影响。文献[23]基于商誉模型，构建了一个制造商和一个投资绿色广告的零售商组成的闭环供应链微分博弈模型。也有学者研究了三级闭环供应链[24～25]，文献[24]研究了由一个制作商、一个零售商和一个投资研发、广告和大数据营销的互联网服务平台组成的三级闭环供应链，并由零售商回收的微分博弈模型。文献[25]在第三方回收的三级闭环供应链中考虑了公平关切和回收率随机扰动的影响。随着研究的深入，许多学者将供应链参与者的行为因素考虑进来[26～29]。文献[26]引用伊藤过程来描述回收率的变化，研究了由制造商主导，零售商回收且具有公平关切的闭环供应链。文献[27]分别构建了制造商关注零售商的公平关切、制造商不关注零售商的公平关切，由零售商回收的闭环供应链微分博弈模型。文献[28]研究了第三方回收商的公平关切行为对闭环供应链的影响。文献[29]则进一步把政府相关的因素考虑进来，探讨了在政府规制下，制造商分担零售商宣传成本的闭环供应链。本文则研究创新产品由第三方回收，制造商分担回收成本的三级闭环供应链，寻找在此种情景下各种决策变量的最优路径。

为了研究商业和经济领域中的动态广告问题，学者们建立了各种动态需求函数或市场份额函数[30～32]。文献[30]建立了经典的NA模型来描述商誉的动态变化并进一步影响需求变化。文献[31]提出了V-W模型，考虑了广告对销售的影响，这种影响通常持续到当前时期之后，其影响会逐渐减弱。文献[32]引入Lanchester模型来分析竞争广告问题。上述模型在动态供应链中已有不少应用，但鲜有文献在动态供应链中考虑市场扩散模型，在闭环供应链中的应用更是没有。在现实生活中，对耐用产品的需求往往会经过市场扩散过程而达到产品的累计销售，在这种情况下，市场中的一些人并不是立即购买该产品，而是通过与媒介或口碑的接触之后从而产生购买的意愿[1,33～34]。文献[1]考虑了这种扩散过程建立了市场扩散模型。文献[33]在Bass模型基础上进一步考虑了价格的因素。文献[34]将Bass的创新产品扩散模型引入到开环供应链中来刻画市场的即时需求，研究了由一个供应商主导和一个零售商跟从的主从动态微分博弈过程。

经典文献还未见到把Bass模型应用于闭环供应链之中。本文在上述文献的基础上，用Bass模型来建立一个由制造商主导，零售商和第三方回收商跟从的闭环供应链微分博弈模型，同时考虑在无政府规制下，制造商主动分担第三方回收商的一部分回收努力成本，在此基础上，寻找闭环供应链各成员的最优决策路径。本文的主要创新点在于：（1）将Bass模型引入由制造商主导，零售商和第三方回收商构成的三级闭环供应链，并建立动态微分博弈模型；（2）考虑了制造商分担回收商回收努力成本对供应链各成员及整个供应链上各决策变量的影响。本文与其他文章主要的区别在于在闭环供应链中使用Bass模型来刻画市场中的非线性动态需求的变化，这是其他学者还未研究过的领域，扩展了符合Bass模型的创新产品的闭环供应链研究。

一、模型假设

本文的闭环供应链系统由一个占主导地位的制造商，记为M（Manufacturer）；一个零售商，记为R（Retailer）；和一个负责回收的第三方回收商，记为T（Third-party Recycler）组成。

设w(t) 为t时刻制造商制定新产品的批发价（本文假设全新产品与再制造产品完全同质），是制造商的控制变量；p(t) 为t时刻零售商制定新产品的零售价，是零售商的控制变量；cm为新产品边际生产成本；cr为再制品边际生产成本； Δ=cm-cr为再制造产品节省的成本；r(t) 为t时刻第三方回收商的回收努力，是回收商的控制变量，为回收商的回收努力成本，是回收努力的二次函数；假设t时刻制造商支付回收商的累计回收费用与回收率τ(t) 呈 正比关系，即为 γτ(t) ， γ表示单位时间内回收率为1时的制造商总支付，则单位时间内回收费用为； φ为制造商分担回收努力成本的比例；T为新产品投入市场的总时长；N为市场消费者的总数（包括潜在消费者和现实消费者）。

Bass模型的数学来源是可靠性理论中得到广泛应用的可靠度函数模型。将市场需求总量等同于可靠度函数中的“总实验数”，在t时刻已卖出的商品数等同于可靠度函数中的“累积失效的产品数量”，在t时刻还未卖出的商品数等同于可靠度函数中的“仍然完好的产品数量”，t时刻创新产品市场占有率x(t)等同于可靠度函数中的概率分布函数F(·)。因此，使用Bass模型可以很好地刻画出新耐用产品闭环供应链的动态博弈演化过程。

创新产品是指某种研发出的新产品或对某一老产品进行创新改造后的产品，如不断更新换代的手机等电子产品，创新产品在上市后将会在消费者市场中进行扩散，通过宣传、推广和消费者之间口头传播逐渐累积销量。学者们证明了创新产品进入市场后的规律服从Bass模型[1,32～33]，即创新产品在消费者之间存在一个扩散的过程。假设每一个消费者只会购买一次该创新产品且市场的消费者的总数为N，将购买了该产品的消费者称为现实消费者，而未购买该产品的消费者称为潜在消费者。则t时刻现实消费者的比例为x(t)，即该产品的市场占有率，且满足[32]，x(0)=0。其中j(1-x(t))为因消费者自己的喜好或广告等因素使得潜在消费者购买该产品的部分，与潜在消费者比例 1 -x(t)呈 正比，称j为 消费偏好系数；kx(t)(1-x(t))为因现实消费者对潜在消费者的传播引起潜在消费者购买的部分，既与潜在消费者呈正比，又与现实消费者呈正比，称k为模仿系数。可以得到t时刻该创新产品的需求量。根据文献[33]，考虑需求弹性ε与价格p呈负相关，即，可得， 进一步D∝e-ap，即需求量与e-ap成正比，又因需求量，因此可假设，其中a为价格对潜在消费者向现实消费者转换的影响系数。

事实上，即时产品回收率具有“累积效应”特征，即一个时期的回收率是过去累积回收努力的函数[18]。根据文献[18]，将回收率设置为状态变量，其变化率为回收努力和回收率的函数，满足，τ(0)=0。其中 α为回收努力对回收率的影响系数， β为回收率的衰退系数。

二、模型建立与求解

在此闭环供应链中，制造商、零售商和回收商构成制造商主导零售商和回收商跟从的Stackelberg博弈，制造商先决定其批发价格w(t)，随后零售商决定零售价格p(t) ，回收商决定回收努力r(t)。得到制造商的长期利润函数为：

零售商的长期利润函数为：

回收商的长期利润函数为：

则制造商、零售商和回收商的目标函数分别为：

命题1：在创新产品闭环供应链中，制造商的最优批发价w∗(t)为：

零售商的最优零售价p∗(t)为：

回收商的最优回收努力r∗(t)为：

证明：

由博弈顺序，先计算回收商的最优回收努力和零售商的最优零售价格。

回收商的Hamilton函数为[35～36]：

所以

零售商的Hamilton函数为：

由

和横截条件 λR(T)=0，解得：

最后计算制造商的最优批发价，制造商的Hamilton函数为：

由

解得

所以

证毕！

推论1：创新产品闭环供应链中，制造商的最优批发价虽然是随着时间变化而变化的，但是每一件新产品的边际利润都为，即制造商要取得最大利润的最优批发价策略，就要使得每一件新产品的边际利润为。且批发价和零售价都随着回收率的增加而减少。

证明：

由式(8)可以看到制造商的最优批发价w∗(t)是随着时间变化而变化的，且t时刻的批发价w∗(t)减去t时刻的单位成本 (cm-Δτ(t))可得产品的边际利润为。由于可知批发价和零售价都随着回收率的增加而减少。

证毕！

推论2：当模仿系数大于消费偏好系数(k-j＞0)时，即现实消费者对潜在消费者购买的影响大于潜在消费者的创新购买效应影响时，零售商定价使得每件产品的边际利润随着现实消费者的比例在范围内增加而提高，随着现实消费者的比例在范围内增加而降低；当模仿系数小于或等于消费偏好系数(k-j≤0)时，即潜在消费者的创新购买效应影响大于现实消费者对潜在消费者购买的影响时，零售商定价使得每件产品的边际利润随着现实消费者的比例的增加不断减小。

证明：

证毕！

命题2：在创新产品闭环供应链中，创新产品最优的市场占有率路径x∗(t)为：

最优回收率路径 τ∗(t)为：

证明：

最优回收率的路径 τ∗(t)的证明见命题1的证明。

由命题1得：

且x(0)=0可得：

当t=T时，x(T)=B(T)(j+kx(T))(1-x(T))解得：

或

证毕！

推论3：在创新产品闭环供应链中，回收商的回收努力程度随时间逐渐减小，在新产品刚推出不久时回收力度最大，随着推出时间的延续，回收力度逐渐减小，当产品退出市场时（即T时刻时）回收力度减少到0。

证明：

证毕！

推论4：在创新产品闭环供应链中，选择的销售时长越长，产品退出市场时的市场占有率x(T)会越高，最终销售量Nx(T)也会越大。

证明：

根据式(30)，将X(T) 对T求偏导可得由于B′(T)＞0 且，可知。 即T越大，x(T)越大，Nx(T)也越大。

证毕！

由推论3可知，在创新产品刚进入市场时回收商的回收努力最大，随后随着销售时间的增长不断减小其回收努力，直到创新产品退出市场，将不再回收该产品。相应的回收率先因回收商做出的回收努力而快速增长，后因回收商的回收努力在不断减弱，在回收率达到最大后再开始衰退。在现实生活中很多产品在刚推出时其产品回收宣传力度很大并维持较长的一段时间，回收率也在不断增长；但随着产品的推出时间增长，回收努力渐渐减弱，而回收率也达到顶峰开始衰退；当产品接近退出市场时，产品的回收宣传力度会大幅下降；而当产品退出市场时，将不再回收该产品。由推论4可知产品的销售时间越长，其最优策略下销售量就会越大。这些结论都和现实的情况相符合。

将各变量代入式(1)～式(3)可得制造商、零售商和回收商的最优整体长期收益分别为：

三、数值分析

假设该闭环供应链各项参数如下：cm=20，cr=10，Δ=10，a=0.01 ，kT=200，γ=100，α=0.3，β=0.5，T=30，N=10 000 ，φ=0.7。考虑不同的市场情形（即不同的消费偏好系数j和模仿系数k）对闭环供应链的影响。

1. 不同市场情形对闭环供应链的影响

首先，考虑不同市场情形对T时刻现实消费者的比例的影响。

由图1可见随着消费偏好系数j和模仿系数k的增大，T时刻现实消费者的比例也会增大。且消费偏好系数和模仿系数较小的时候，曲面斜率较大，而在消费偏好系数和模仿系数较大时，曲面平缓。在消费偏好系数和模仿系数较小时，如j=0.1，k=0.1时，x(T)=31.57% ，当j增大到0.2时，x(T)=46.36% ，增长14.79%；当k增大到0.2时，x(T)=38.24%，增长6.67%。而在消费偏好系数和模仿系数较大时，如j=0.8 ，k=0.8 时，x(T)=83.76%，当j增大到0.9时，x(T)=84.70%，增长0.94%；当k增大到0.9时，x(T)=84.56%，增长0.80%。

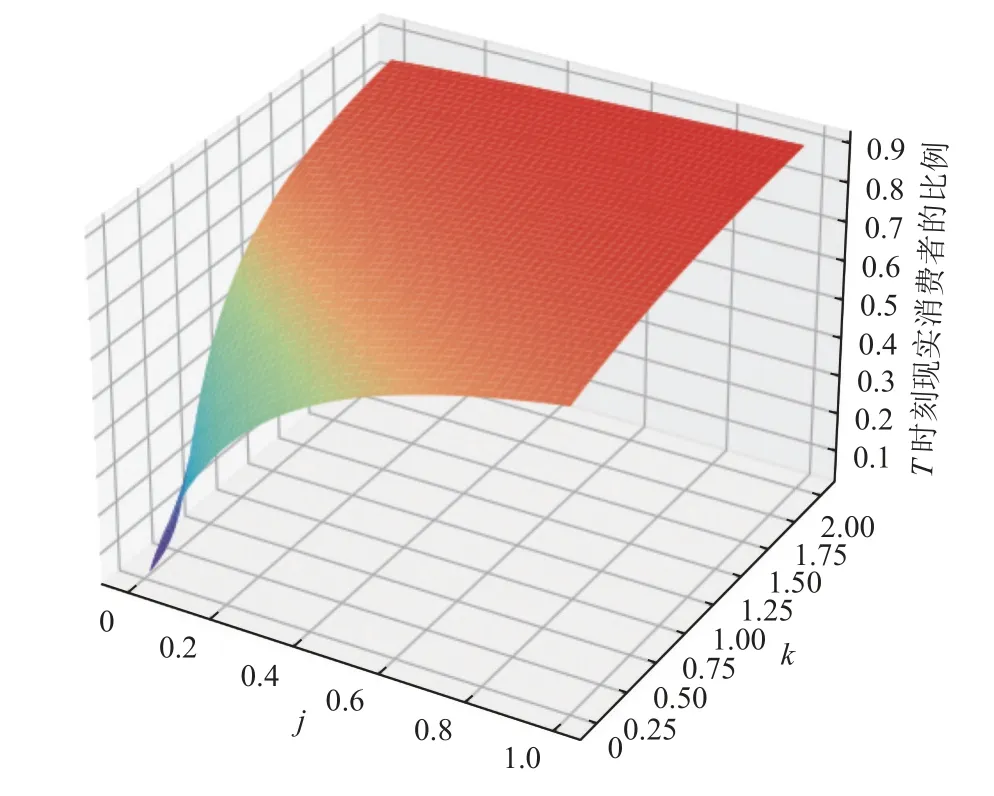
图1 参数j、 k与 T时刻现实消费者的比例的关系图

然后考虑不同市场情形对闭环供应链及供应链各成员的整体长期利润的影响。

由图2可发现，随着消费偏好系数j和模仿系数k的增大，制造商的整体长期利润 πM、零售商的整体长期利润 πR都会增大，而第三方回收商的整体长期利润 πT不变；所以整个供应链的整体长期利润πH也会增大。且在消费偏好系数和模仿系数较小时，如j=0.1，k=0.1时 ， πM=312 355， πR=338 230。当j增大到0.2时， πM增长147 776， πR增长238 068；当k增大到0.2时， πM增长66 560，πR增长45 334。而在消费偏好系数和模仿系数较大时，如j=0.8，k=0.8 时， πM=834 104 ， πR=1 588 631 。当j增 大到0.9时， πM增长9 372， πR增长73 022；当k增大0.9时， πM增长8 001， πR增长28 287。

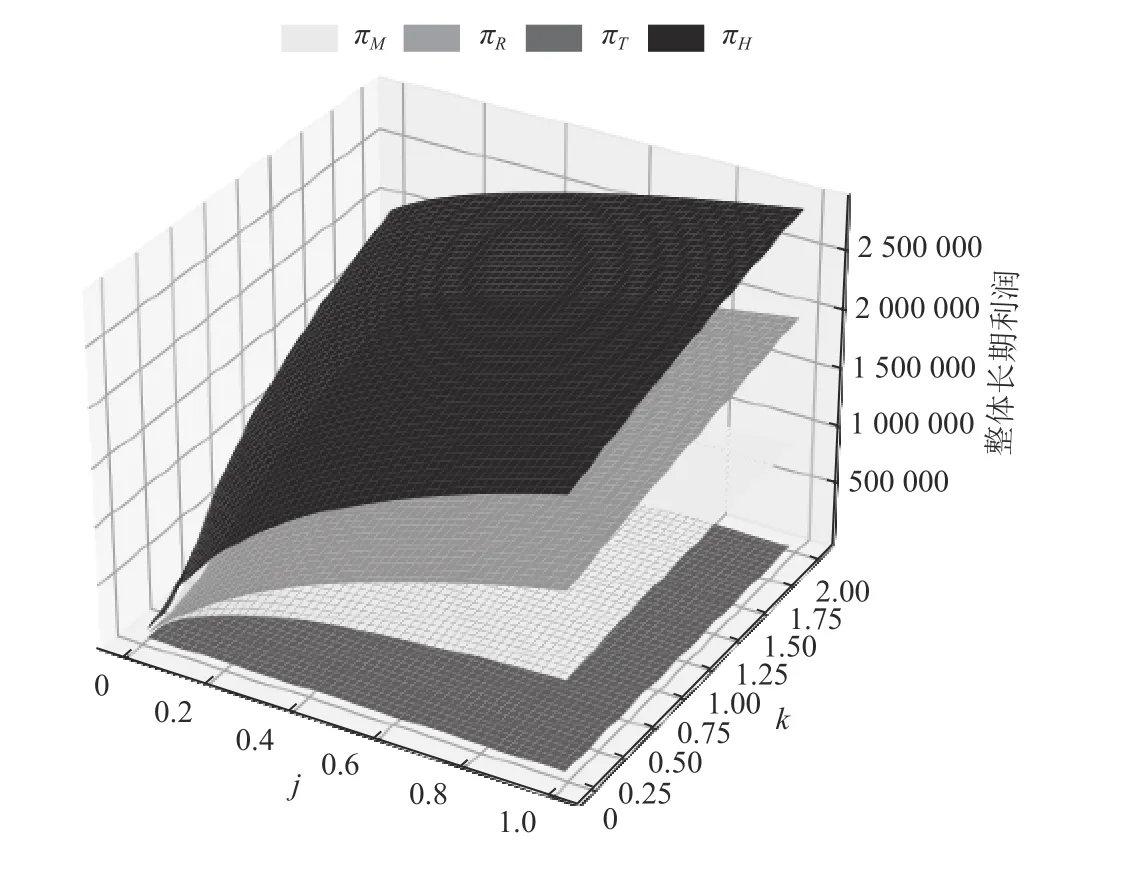
图2 参数j、 k与供应链及供应链各成员利润的关系图

由上述分析可知，在消费偏好系数和模仿系数都较高的市场下，产品销售末期现实消费者的比例也比较高，即在这样的市场下能销售出更多的产品，并且制造商和零售商能得到更高的整体长期利润，整个供应链的整体长期利润也将更高。同时发现消费偏好系数和模仿系数较低时，通过广告努力来增大消费偏好系数和模仿系数能明显提高销售量和制造商、零售商利润。而消费偏好系数和模仿系数较高时则效果不明显。消费偏好系数越大，说明该创新产品对某些特定的客户群有吸引力；模仿系数越大意味着引起效仿的客户群体越大；从而导致创新产品在市场上的扩散速度越快，即在固定的销售时间内的销售量将越大。因此，制造商、零售商都能获得更高的利润，致使整个供应链的利润也会更高，且在消费偏好系数和模仿系数较小时，增大消费偏好系数和模仿系数的边际收益较大。

2. 回收成本分担比例对闭环供应链的影响

接下来，分析制造商的回收成本分担比例对闭环供应链的影响。通过软件计算发现在不同市场情形下都存在一个最优的成本分担比例 φ∗，当制造商采取这个最优的成本分担比例 φ∗时，制造商获得的利润最大，不同市场情形时的 φ∗值如下图所示。

进一步计算了不同市场情形下，制造商采取其最优成本分担比例时零售商和回收商的利润，并与制造商不分担成本时进行比较，如下图所示（以下几个图中的制造商均釆用最优分担比例）。

从图3中可以看到在不同的市场情形下都存在一个制造商最优成本分担比例且不等于0。从图中可以发现，制造商的最优成本分担比例先随着消费偏好系数和模仿系数的增大而增大，在j=0.1，k=0.5左右的时候最大，随后随着消费偏好系数和模仿系数的增大而减小。从图4和图5可以看到，在不同的市场情形下，制造商采取最优分担成本比例能提高零售商和回收商的利润。由图6可以看出，制造商分担回收成本时，能明显提高创新产品的回收量，提高创新产品的回收效率。

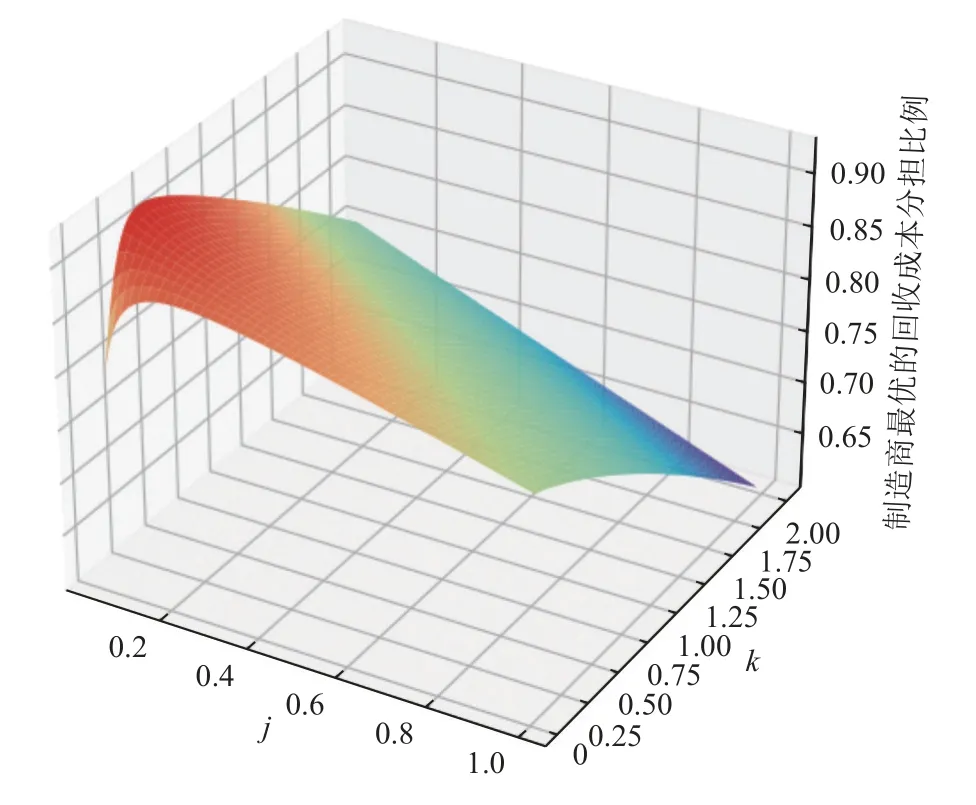
图3 不同市场情形下的制造商最优成本分担比例

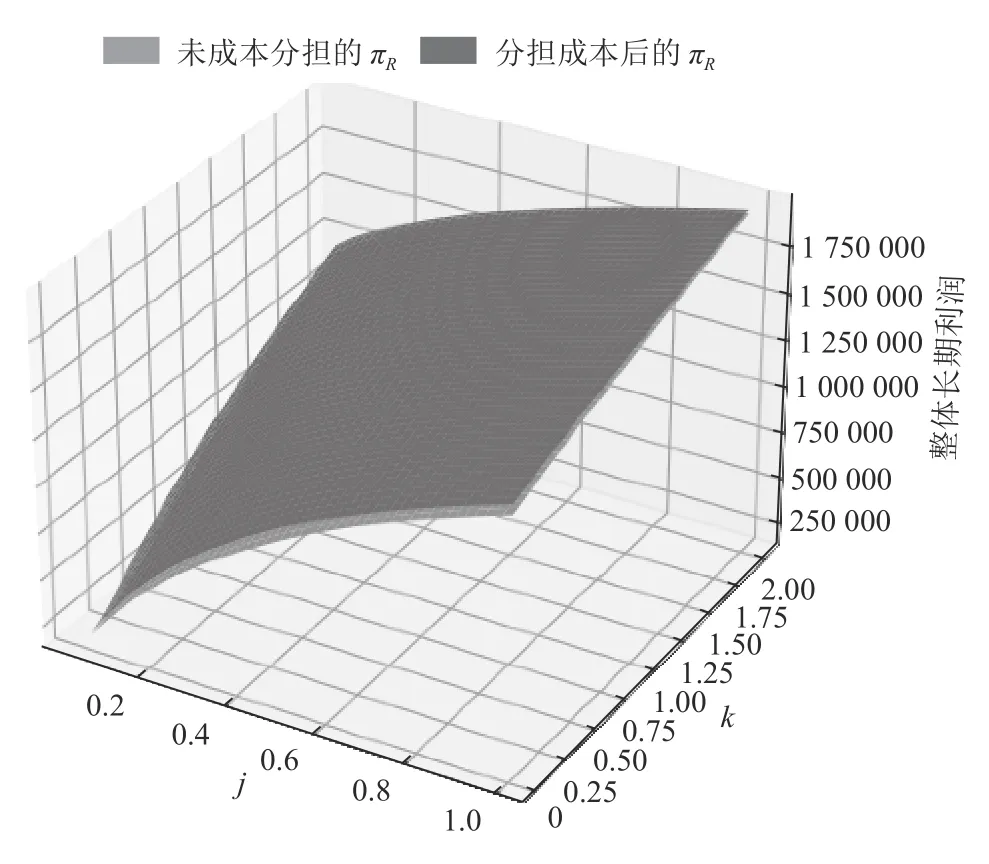
图4 制造商分担成本时与不分担时零售商利润对比

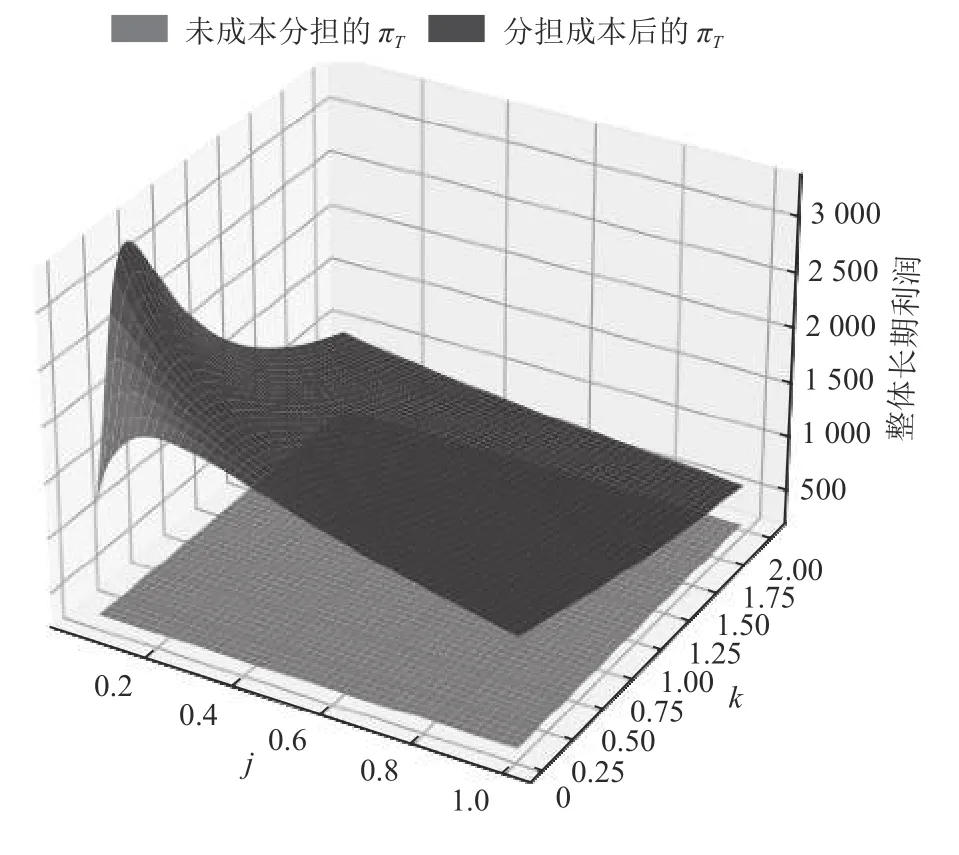
图5 制造商分担成本时与不分担时回收商利润对比

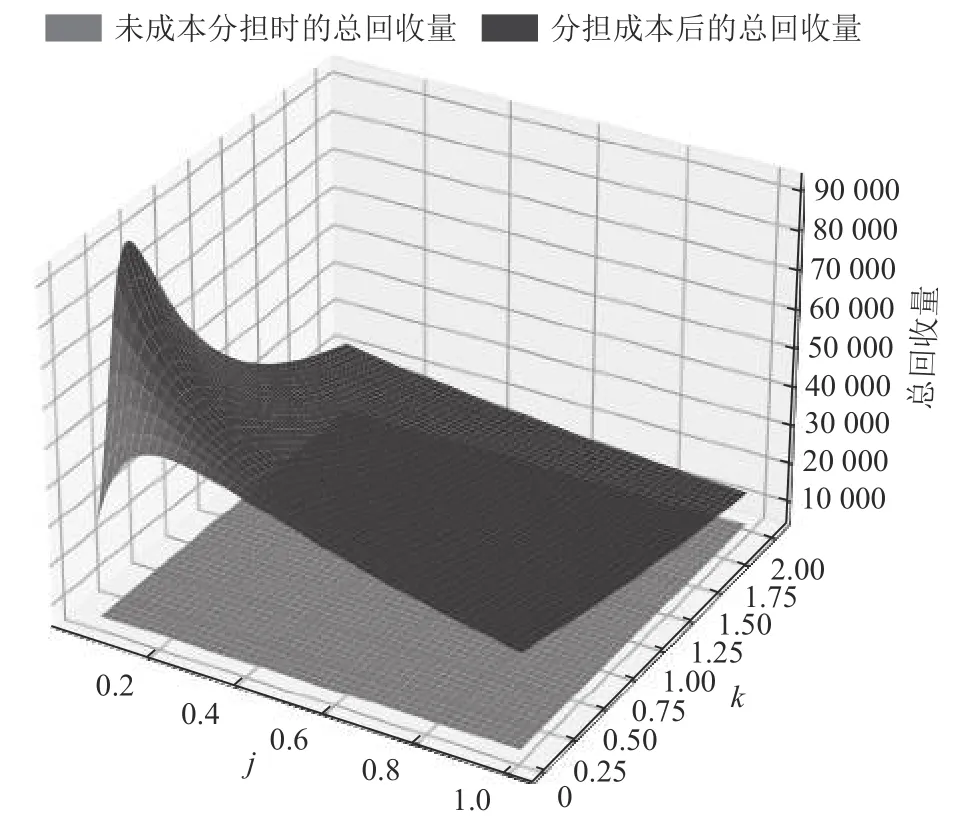
图6 制造商分担成本时与不分担时创新产品的回收数量对比

由上述分析可知，制造商分担回收商回收成本，提高了闭环供应链的回收率，增大了回收商的利润，提高了创新产品的回收量，同时减少了制造商的平均制造成本，进而提高了制造商和零售商的利润。但随着回收努力成本分担比例的增大，其对制造商带来的边际效益不断减小，因此能得到最优的回收成本分担比例。且在不同的市场条件下总存在一个最优的成本分担比例，使制造商的整体长期利润最大。

在消费偏好系数和模仿系数较小时，此时供应链的销售量较小，需要加大回收努力成本的分担比例，以降低创新产品的平均成本，来增加供应链的利润。在消费偏好系数和模仿系数较大时，此时供应链的销售量较大,过高的回收努力成本将给制造商带来负收益，同时造成供应链的利润减少，因此需要适当减小回收努力成本的分担比例来增大供应链的利润。由图2和图5可以发现，在闭环供应链中相比制造商和零售商，第三方回收商的利润是相当低的，所以它应该同时对多种商品进行回收，这样才能增加收益。

四、结束语

（一）结论

本文基于Bass模型（创新扩散模型）建立了一个制造商主导、零售商和第三方回收商跟从的闭环供应链模型，通过最优控制方法得出了制造商批发价格的最优路径w∗(t) ，零售商的零售价p∗(t)和回收商回收努力的最优路径r∗(t)，进一步得到市场占有率x(t) 、回收率 τ(t)的最优路径以及制造商、零售商、回收商以及供应链的整体长期利润。并通过仿真分析，得到了制造商最优的回收成本分担比例。得出的主要结论如下：

1. 通过数值分析，本文发现回收成本分担提高了创新产品的回收效率，减少了制造商的平均制造成本，且提高了闭环供应链各成员的利润。

2. 由图4～图6分析可知，对于制造商来说，在不同的市场条件下总存在一个最优的成本分担比例，且采取这个最优成本分担比例也能提高回收商和零售商的利润。

3. 由图1和图2分析可知，在消费偏好系数和模仿系数高的市场中，制造商和零售商能获得更高的利润，且通过广告等销售努力来提高消费偏好系数和模仿系数能售出更多的创新产品，提高制造商和零售商的利润。

4. 由推论1～推论4可知，制造商和零售商的最优定价都是随时间变化的，但是制造商的最优边际利润是始终不变的。而回收商的最优决策为先做出最大的回收努力，之后再逐渐减少。

（二）管理启示

结合上述结论，本文对创新产品企业有以下启示：

1. 制造商回收成本分担能提高闭环供应链所有成员的利润，并提高回收商对创新产品的回收努力水平，能使更多的废旧产品回收再利用，应当大力推广。

2. 制造商在协商回收成本分担比例时要小心谨慎，因为不同的市场存在着不同的最优分担比例。

3. 制造商和零售商可以通过一定的广告等销售努力，来加快创新产品在消费者之间的扩散，以此提高销量，获得利润。

4. 回收商应在前期做出大量的回收宣传和准备，尽快地提高消费者的回收意识，使创新产品的回收率迅速达到较高的水平，之后就能用较低的回收成本维持这个较高的回收率。

（三）展望

本文的研究是以市场完全垄断为前提，只考虑了一个占主导地位的供应商和一个处跟从地位的零售商和第三方回收商销售创新产品时的闭环供应链的情形，并且假设再制造产品于新生产的产品没有区别。与主流的动态供应链研究不同，本文没有采用经典需求模型或者商誉模型来刻画需求的变动，而是使用bass模型来描述创新产品在闭环供应链市场中的扩散，为之后的闭环供应链研究提供了新思路。将来还可以考虑一个供应商两个零售商一个回收商，两个供应商一个零售商一个回收商或者一个制造商一个零售商两个回收商竞争等寡头垄断的情形；或者考虑再制造产品与新生产的产品有一定区别，并且存在消费者产生购买事后后悔和购买切换后悔等情形。