基于Weibull分布的高温结构性黄土统计损伤本构模型

2023-12-14王尚杰李曾乐

长江科学院院报 2023年12期

郅彬,王成,王尚杰,李曾乐,白鹤

(1.西安科技大学建筑与土木工程学院,西安 710054; 2.中国电建集团西北勘察设计研究院有限公司,西安 710065)

0 引言

能源桩是利用地表的地热能作为能量源的一种新型建筑节能技术,利用温差循环传热介质实现桩与桩周土体的热交换。工作时会引起桩周岩土体的温度变化,而温度变化对黄土结构性影响较大,使土体遭受不同程度的破坏。因此对高温作用下结构性黄土力学性能进行分析是建立统计损伤本构模型的关键。

近年来,为从不同角度分析温度对结构性黄土力学性质的影响,许多专家学者通过大量试验进行本构模型研究。陆嘉楠等[1]研究表明粉质黏土温度越高,土体固结速率越快,固结体应变越大。王瑞等[2]研究发现温度越低,高原土体的应力软化特性越明显,黏聚力和内摩擦角随温度的升高而逐渐减小。马宝芬等[3]对冻融循环作用下重塑黄土抗剪强度的影响进行研究。Zhang等[4]研究了温度对马兰黄土渗透性的影响以及传统温度校准公式(Traditional Temperature Calibration Formula,TTCF)的适用性。Wang等[5]为确定高温对黄土多孔分布的影响,采用核磁共振测试方法得到了黄土在不同温度下的拉伸破坏载荷。Zhou等[6]研究冻结黄土变形过程中的损伤演变和力学性能的再结晶增强。

有专家学者对土体本构模型做了大量研究。 Zhi等[7]提出了可以在高应力状态下描述结构性黄土应力-应变特性的模型。Lai等[8]研究了围压对冻土力学性质的影响机理,得到冻土的弹塑性增量本构模型。Fu等[9]基于室内试验和本构模型,提出饱和黄土的本构模型。Wang等[10]利用结构参数建立了原状黄土的动态本构关系。

研究发现,温度对结构性黄土内部胶结物质有一定的破坏,但目前关于高温条件下结构性黄土损伤本构模型研究较少,损伤本构模型大部分都应用于岩石和冻土。

沈珠江[11-12]在弹塑性理论和损伤力学理论基础上提出了一个可以适用于黄土的非线性损伤力学模型,并与广义屈服面模型进行比较[13]。夏旺民等[14]提出黄土的损伤变量、增湿损伤和加载损伤的定义及其关系,并提出黄土弹塑性损伤本构模型。谢星等[15]运用统计损伤理论建立了考虑损伤门槛的损伤本构方程。郅彬等[16]基于二元介质模型,建立了考虑中溶盐含量的结构性黄土强度准则。罗爱忠等[17]在沈珠江双硬化参数模型的基础上,引入结构性参数,建立了双硬化参数模型。Cai等[18]对冻土的损伤变量进行了研究。Chen等[19]通过试验确定应力状态和动荷载类型对饱和黄土动力特性及损伤演化的影响。Song等[20]为研究高温对黄土断裂破坏的影响,对不同预制裂缝的半圆形高温处理的黄土试样进行了三点弯曲试验。Luo等[21]提出能反映原状黄土完整结构损伤发展规律的结构损伤特性参数,并建立了结构性黄土本构模型。

Yao等[22]建立了非饱和原状黄土弹塑性损伤模型(Elastoplastic Damage Model,EDM)和湿陷性黄土的弹塑性损伤-渗流-固结耦合模型(Elastoplastic Damage Seepage-consolidation Coupled Model,EDSCM)。张德等[23]通过引入修正的M-C屈服准则来描述冻土微元强度的破坏准则,建立能反映冻土破坏全过程的损伤本构模型。

目前,国内外学者对于土体温度变化的研究大都基于冻融循环和低温条件,而对高温条件下结构性黄土损伤本构模型和细观结构的影响研究较少。因此本文基于西安地区Q2黄土对高温条件下不同围压结构性黄土进行研究,对室内三轴试验和核磁共振试验结果分析,假定黄土微元强度服从Weibull分布,构建了高温条件下结构性黄土统计损伤本构模型,并对模型进行验证。

1 试验方案

1.1 试验土样

本文选用的土样为西安某地基工程现场黄土,试验土样为人工取土。土样埋深在14～16 m范围内,呈褐黄色、可塑、稍湿、大孔发育,按照《土工试验方法标准》(GB/T 50123—2019)[24]对选取的土样进行标准制样,直径39.1 mm、高度80 mm,测得的物理力学指标见表1。

表1 黄土的物理力学指标

1.2 试验方案及试验仪器

1.2.1 三轴试验

本文试验仪器选用TKA-TTS-1WS全自动温控三轴仪,如图1所示,进行试验之前先对试验仪器进行校准。

图1 TKA-TTS-1WS全自动温控三轴仪

温度会对黄土结构性和力学性质产生较大影响[25],为测得土体的抗剪强度指标,试验前先在不同温度下对试样进行固结试验,然后对原状黄土试样在不同温度和不同围压下进行三轴固结不排水试验,可得到应力-应变关系。根据GB/T 50123—2019[24],试验中剪切速率为0.08 mm/min,分析原状黄土的颗粒结构损伤和抗剪强度。当试验中轴向应变达到15%或有明显破坏现象出现时试验终止。试验严格按照GB/T 50123—2019[24]进行。试验方案见表2。

表2 原状黄土固结不排水试验方案

1.2.2 核磁共振试验

核磁共振仪采用NMRC12-010V核磁共振孔隙分析仪。核磁共振仪如图2所示。

图2 核磁共振仪

核磁共振的基本原理是由外磁场作用引起的核自旋能级的跃迁。

核磁共振技术可以有效测量结构性黄土内部孔隙数量和分布特征及结构特征。结构性黄土孔隙水的孔隙水驰豫时间T2可表示为扩散弛豫时间T2D、自由弛豫时间T2B和表面弛豫时间T2S,即

(1)

流体中的弛豫时间主要由表面弛豫决定,自由弛豫和扩散弛豫可忽略不计,表面弛豫时间可表示为

(2)

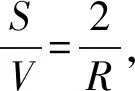
(3)

本试验分别对不同温度下原状黄土进行核磁共振试验,试验中的参数为:共振频率12 MHz,磁体强度为(0.3±0.05)T,线圈直径为60 mm,磁体温度为32 ℃,脉宽P1为11.00 μs,脉宽P2为21.04 μs,采样等待时间TW=1 000 ms。

2 试验结果分析

2.1 原状黄土试验结果分析

原状黄土相同温度不同围压下的主应力差-轴向应变曲线,如图3所示。

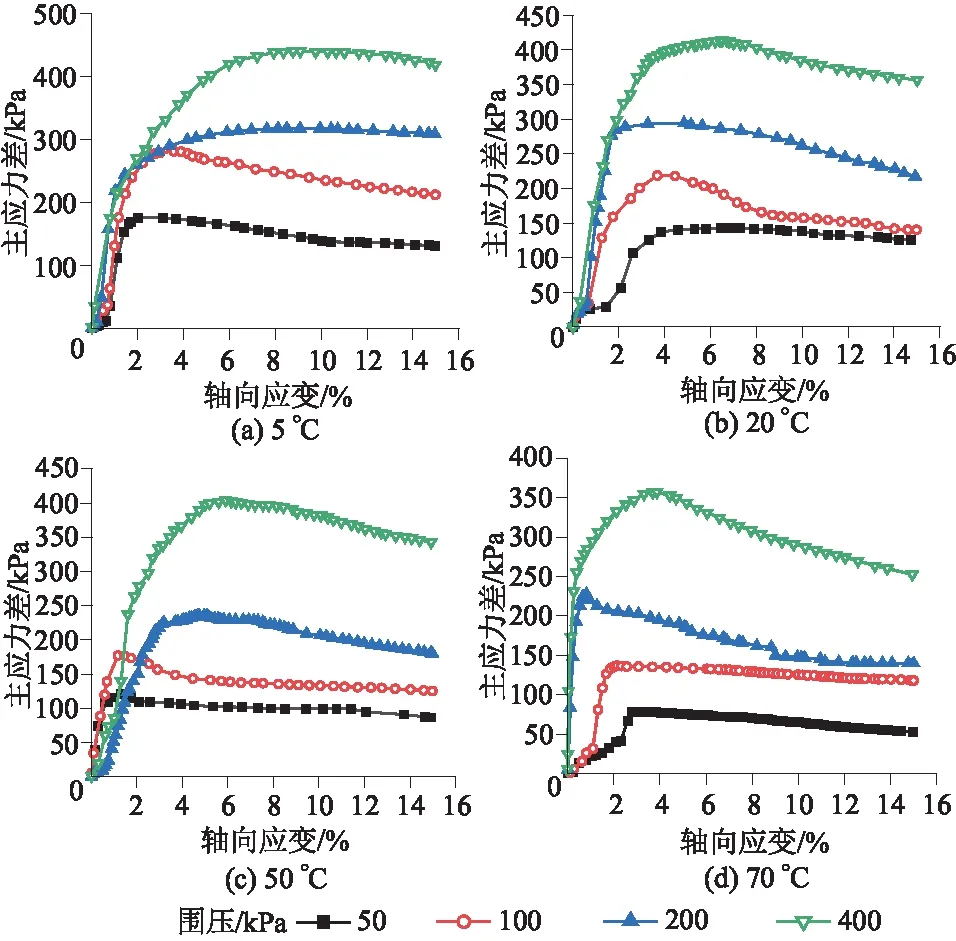
图3 原状黄土不同围压下的主应力差-轴向应变曲线

由图3可知,原状黄土的主应力差随轴向应变的增加而先升后降,对比发现,曲线的峰值在低围压下趋向平稳,在高围压下下降幅度更明显,即出现软化现象。

在小变形荷载作用下,土体的强度主要由颗粒骨架间的胶结物质和土体颗粒骨架承担,当达到某一临界值时,土体颗粒骨架和土颗粒间的摩擦作用可承担的外荷载达到最大,即主应力差-应变曲线峰值点。当土体变形达到某一值时,在外荷载作用下,土体内部的颗粒骨架发生破坏,土体强度失效,此时,全部由土颗粒间的摩擦作用抵抗外部荷载。但是由于后期的摩擦作用不足以替代土体颗粒骨架提供的强度作用,即出现应变软化现象。

随着温度的升高,在200 kPa和400 kPa的围压下,峰值点向左移动,即在应变很小时,曲线达到峰值点,应变软化现象更加明显;50 kPa和100 kPa围压下,峰值逐渐减小,5 ℃时,应变较小时达到峰值,20 ℃到50 ℃,峰值应变逐渐减小,70 ℃时,由于高温作用对黄土结构性破坏,峰值点土体应变有所增加,逐渐趋于硬化。根据损伤理论,原状黄土在开始阶段,土体受到的剪应力较小,土体颗粒并未滑移,土体骨架未产生损伤,接着由于剪应力的增大,土体的部分颗粒骨架产生滑移和损伤,即在土体骨架中存在完好的骨架和损伤的骨架。随着剪切过程的不断持续,土体胶结物质和颗粒骨架随着温度的升高破损增大,因而曲线峰值点会逐渐向更小的应变轴移动,即应变软化现象随温度的升高愈加明显。

5 ℃时,原状黄土的主应力差达到最大,随着温度的逐渐升高,主应力差峰值也逐渐减小,结构性黄土内部的胶结物质和颗粒骨架随着温度的升高逐步破坏。在高温下,主应力差峰值点之后下降得更为明显,说明结构性黄土内部的胶结物质和颗粒骨架破坏速率更高,曲线在小应变时快速上升而后下降,达到某一临界值时趋于平缓。在低温条件下,曲线峰值点出现在较大应变范围内,并且温度越高偏应力值增长速率越小。

原状黄土相同围压不同温度下的主应力差-轴向应变曲线,如图4所示。

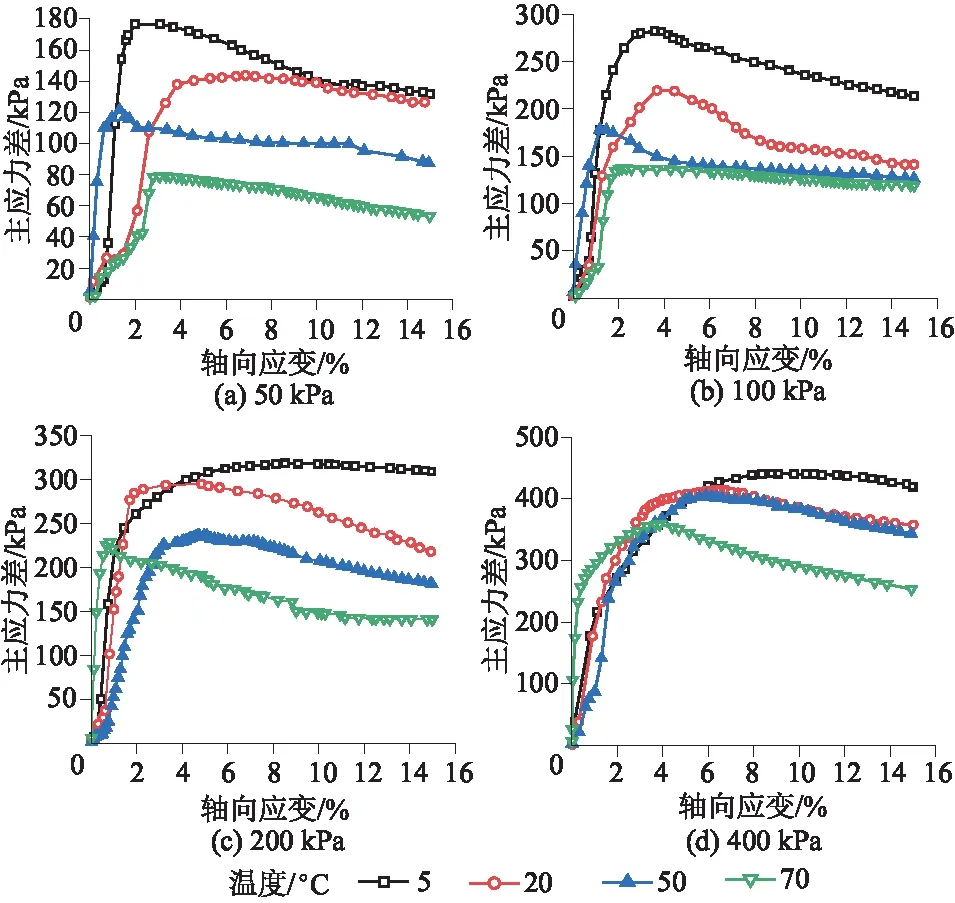
图4 原状黄土不同温度下的主应力差-轴向应变曲线

由图4可知,在同一围压下,随着轴向应变增加,主应力差先增大后减小。温度越高对黄土胶结物质和颗粒骨架破坏越大,在温度的影响下,黄土胶结物质和颗粒骨架的破坏随着温度的减小而减小。在低温低压和高温高压条件下,原状黄土的峰后强度下降得较快。在高温高压双重作用下,原状黄土内部的胶结物质和颗粒骨架破坏得更快,曲线在较小的应变范围内迅速上升然后快速下降;低温低压条件下,原状黄土具有较强的结构性,随着荷载的持续增加,黄土结构性遭到破坏,曲线峰后阶段快速下降。

原状黄土随着温度的升高,土体胶结物质、颗粒和土体内部的孔隙水受热膨胀,降低土体的抗剪强度。围压不变,温度越高,土体内分子运动越剧烈。因此随着温度的升高,土体中离子的活跃度增大,由于土体颗粒间含有碳酸钙等盐类晶体,随着温度的升高,土体内部盐类晶体的溶解度增大,孔隙结构被破坏,孔隙增大、数目增多。土体强度随土体密实度的减小而变小,因此温度会对土体胶结物质和颗粒骨架造成结构性破坏。

2.2 T2谱分布

根据试验结果,绘制不同温度下原状黄土的T2谱,如图5所示。不同温度的原状黄土T2波谱总体上呈三峰分布,主峰主要集中在0.1～1 ms之间,主峰面积占波谱面积的68%以上,其余2个次峰分布在1～10 ms和10～100 ms之间。T2波谱强度变化反映结构性黄土的孔隙体积变化,通过T2波谱面积可计算出不同温度条件的结构性黄土土体内孔隙的数量,进而可反映出结构性黄土随温度增加的损伤变化。温度变化使T2波谱强度发生变化,并且温度越高强度越大。碳酸钙、土体矿物和有机质在各种粒间黏结作用下相互团聚形成胶结物质。随着温度的升高,土体颗粒骨架间的黏结作用较低,胶结物质破坏,碳酸钙被分解,土样孔隙变大,土体内部损伤增多。

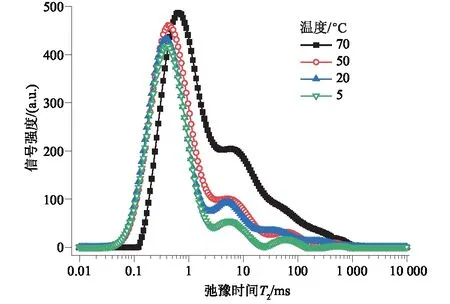
图5 不同温度下原状黄土的T2波谱

根据图5,由于试样孔隙的大小和数目将影响横向弛豫时间T2波谱的面积和波峰分布,并且孔隙大小决定T2波谱峰值的大小及位置分布。原状黄土试样孔隙中的流体为水,由于温度不断升高,孔隙中水分子运动剧烈,土体内部孔隙、裂隙间的孔隙水黏滞系数变小。土体内部存在大量的碳酸钙、部分黏土矿物和少量的有机质,水分可溶解部分胶结物质,由于温度的升高,加快这些胶结物质的溶解,随着温度的持续升高,土体内部可溶解物质的溶解度不断增大,达到饱和,从而破坏土体内部的颗粒骨架,使得试样中土体孔隙变大,水分增多,核磁共振波谱图达到峰值。

土样孔隙的大小和数目将影响横向弛豫时间T2波谱图的面积和波峰分布,试样孔隙越多,水分子所在区域面积越大,并且孔隙大小决定T2波谱面积和峰值的大小及位置分布,因此T2波谱面积和土样中孔隙含水量呈正相关,土样孔隙变化可以通过孔隙含水量从核磁共振T2波谱面积显示,T2波谱面积和温度变化曲线如图6所示。在高温条件下,土体内部的颗粒骨架发生破坏,从而产生更大的孔隙。T2波谱面积可以计算不同温度下土体内部的孔隙大小和数量,进而反映土体温度变化导致的损伤状况。曲线的斜率在50 ℃后达到最大,T2波谱面积的增长速率随之达到最大。

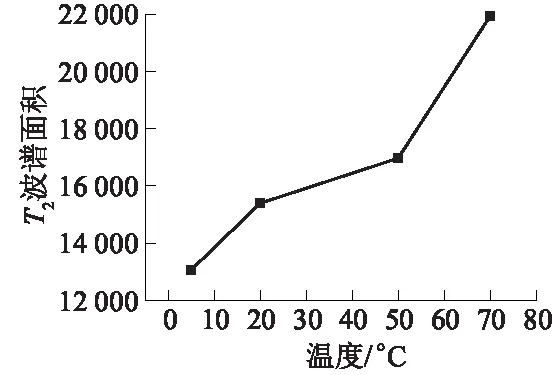
图6 T2波谱面积变化曲线

3 结构性黄土的损伤本构模型的建立

3.1 损伤变量的定义

黄土是一种具有大孔隙的散粒材料,颗粒间的联结主要靠黏聚力和摩擦作用,在外荷载作用下,土体的变形主要来自土体颗粒的破坏和颗粒间接触面的滑移。由于在实际工程中,荷载较大,因此忽略土体颗粒的破坏,土的变形实际是土体颗粒接触面的滑移。在开始阶段,土体受到的剪应力较小,土体颗粒并未滑移,土体骨架未产生损伤,接着由于剪应力的增大,土体的部分颗粒骨架产生滑移和损伤,即在土体骨架中存在完好的骨架和损伤的骨架。假定初始未滑动的颗粒间的联结为无损状态,土体颗粒骨架完全破坏时的状态为完全损伤。

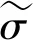
(4)

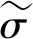
定义损伤变量D为土体受荷状态下损伤的颗粒骨架nr与未受荷状态下完好颗粒骨架n之比,即

(5)

3.2 损伤演化方程

由于土体颗粒非常微小,因此将一个土体颗粒视作一个土体微元强度。假定土体微元强度破坏的概率为P(y),则当加载至某一水平时,已破坏微元的数目[26]为

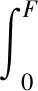
(6)

式中F为微元破坏Weibull分布的分布变量。

则损伤变量[27]为

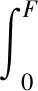
(7)

假定微元强度的分布函数满足Weibull分布,Weibull分布的概率密度函数[23]P(ε)为

(8)

式中:ε为土体的应变量;m和F0分别为形状和尺寸参数,随温度变化。

将式(8)代入式(7)得

(9)

3.3 损伤本构模型

利用应力-应变曲线的峰值特性,对模型参数进行确定,在围压作用下,当土体材料达到峰值强度,即

(10)

式中:σs为峰值应力;εs为峰值应变;σ1和ε1分别为第一主应力和第一主应变。

将式(4)代入式(10)中,得

(11)

式中Ds为峰值点对应的损伤变量。

由式(9)化简可得:

(12)

(13)

土体基于Weibull分布的统计损伤本构方程为

σ1=Eε1(1-D)+μ(σ2+σ3)=

(14)

式中:E为弹性模量;μ为泊松比;σ2和σ3分别为第二、第三主应力。

对于参数m和F0,将式(14)进行移项变形可得

(15)

两边取自然对数,可得

式中m和-mlnF0可分别视为斜率和截距,对式(16)进行线性拟合。

可以令:

(17)

X=lnε1;

(18)

b=-mlnF0。

(19)

则式(16)可化简为

Y=mX+b。

(20)

采用拟合方法可得到参数m和F0。

对于温度作用引起土体的损伤,在研究土体的损伤状态时,通过弹性模量来定义高温作用下的损伤变量Dt,即

Dt=1-Et/E0。

(21)

式中:E0为常温下土体的弹性模型;Et为高温作用下土体的弹性模量。

由于荷载和温度对土体共同作用,本文拟采用耦合的土体损伤演化方法,将常温下土体的初始损伤状态定义为基准态,假定高温作用下的损伤为第一种损伤状态,高温和荷载引起的总损伤状态作为第二种损伤状态,则土体内部损伤本构关系为:

σ=(1-DT)Eε;

(22)

DT=D+Dt-D·Dt。

(23)

式中:DT为考虑高温和荷载共同作用的损伤变量;D·Dt为耦合作用的损伤变量。

将D和Dt代入损伤变量公式中,得

(24)

将上式代入原本构方程中,可得统计意义得土体强度损伤本构模型为

(25)

式中β为土的抗剪传递系数,与温度和围压有关。

3.4 本构模型验证

3.4.1 参数确定

对本文所提出的黄土损伤本构模型进行验证,试验用土取自西安某建筑工地的Q2黄土,在不同温度下进行三轴固结不排水试验,温度分别为5、20、50、70 ℃。计算得模型参数黏聚力c=18.8 kPa,内摩擦角φ=24°,泊松比μ=0.3。对本文所建立的本构模型而言,根据三轴试验数据和温度对模型中的参数进行确定,如表3所示。γ是与温度有关的参数。

表3 模型参数

模型参数m和F0物理力学意义表明[28]:参数m为形状参数,反映材料的脆性及延性特性,m越大,材料的脆性特征越明显,峰值应变越小;参数F0为尺寸参数,反映材料的强度特征,F0越大,材料的强度越大,抵抗破坏的能力越强。

根据模型参数m和F0随着温度的变化规律对参数进行修正,建立参数m、F0和温度t的关系,进而得出任意温度下的统计损伤本构模型。

由试验数据对参数m、F0拟合得:

F0=a1+b1t;

(26)

m=a2+b2t。

(27)

式中a1、b1、a2、b2均为试验参数,本文中取值分别为8.83、0.91、0.97、-0.009 2。

由于岩石、冻土与黄土力学性质相差较大,且在受荷中土体形变较岩石更为明显,因此本文中假定

εt=γεy。

(28)

式中:εt为黄土土体应变;εy为岩石、冻土应变。

将式(26)—式(28)代入统计损伤本构模型式(14)中,由于岩石应力水平高于土体数倍,因此可得变温条件下结构性黄土的统计损伤本构模型为

σ1=βEε1exp[-(γε1/8.83+0.91t)0.97-0.009 2t]+2μσ3。

(29)

3.4.2 计算结果

本文选取4组温度条件下试验数据进行验证,将求出的m和F0以及试验数据代入统计损伤本构模型式(29),然后绘制理论曲线与试验曲线进行。

为验证所建模型对黄土的适用性,图7—图10为不同温度下试验曲线与理论曲线对比。

图7 5 ℃试验曲线和理论曲线对比

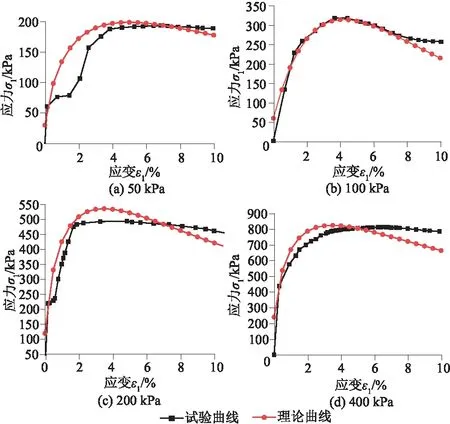
图8 20 ℃试验曲线和理论曲线对比

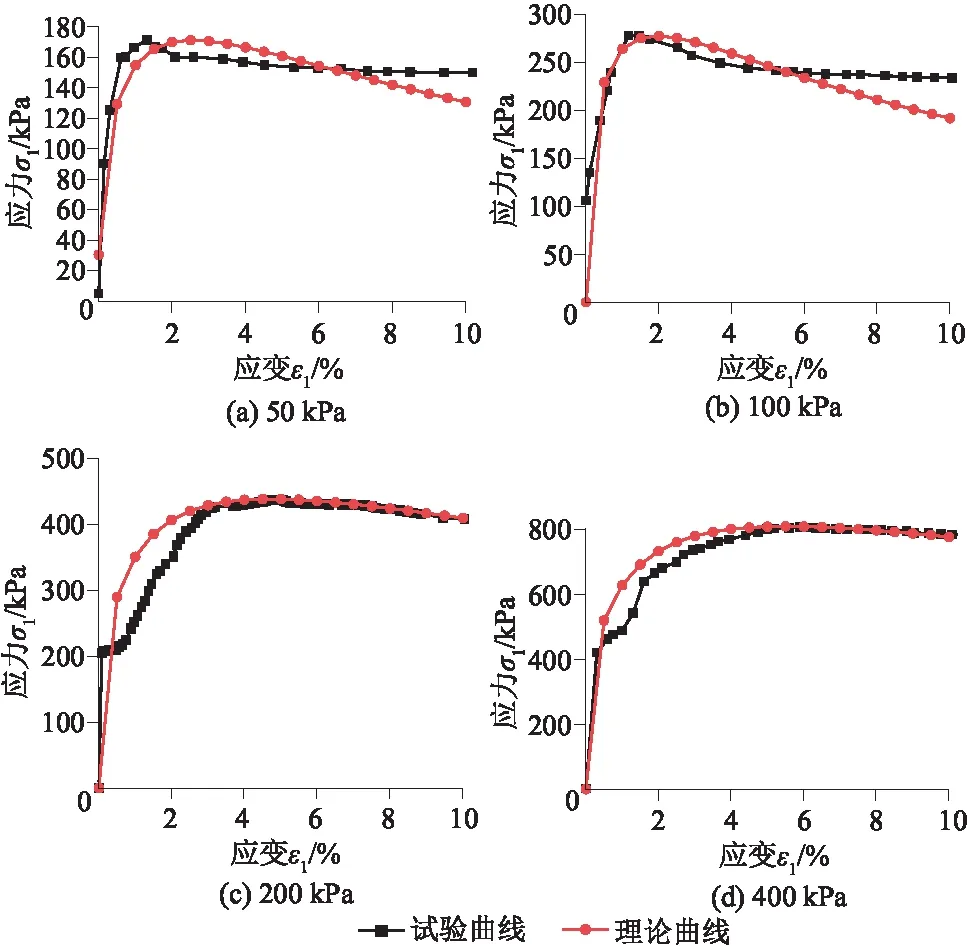
图9 50 ℃试验曲线和理论曲线对比

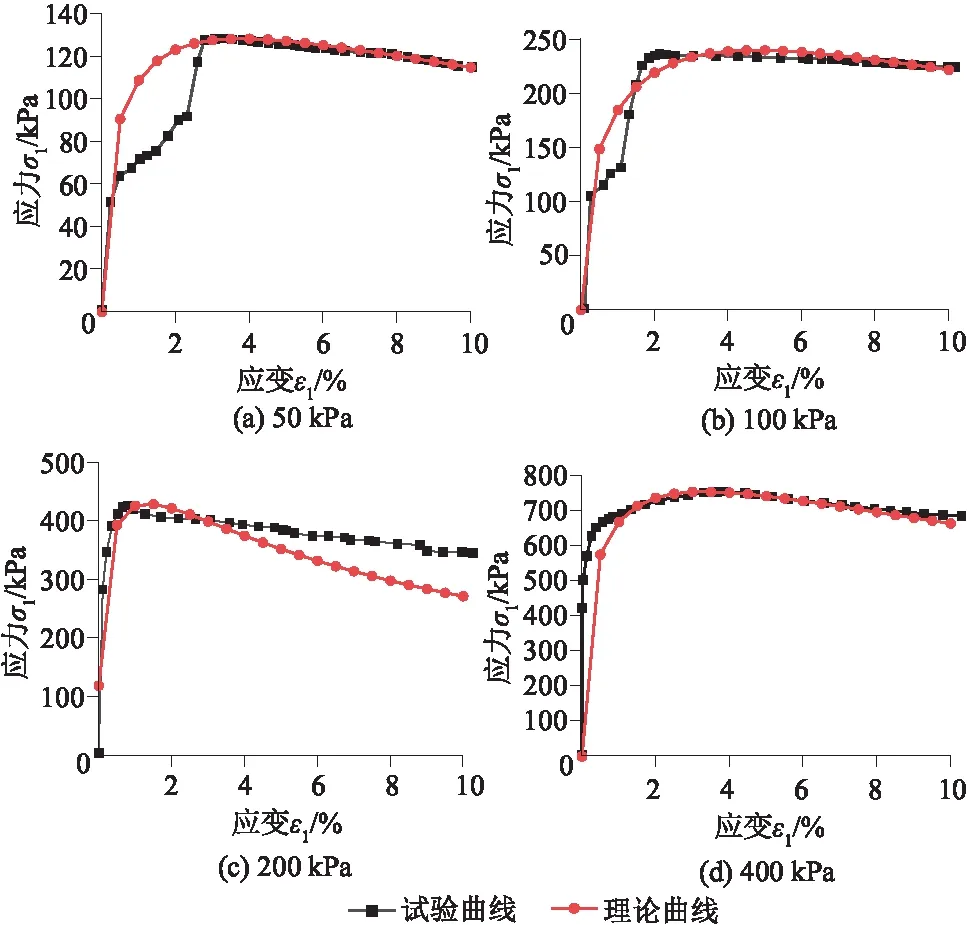
图10 70 ℃试验曲线和理论曲线对比

由图7—图10可知,在相同围压下,随温度不断升高,峰值强度值逐渐降低,试验曲线较理论曲线先达到峰值点,在峰值阶段,理论曲线低于试验曲线。随温度升高,应力在很小的应变范围内增加到峰值,并且峰后阶段应力下降的幅度逐渐减小,曲线均呈先增加后减小,即呈软化型。在70 ℃时,理论曲线可准确地模拟试验曲线的变化规律,拟合效果最好。随温度升高,峰后阶段曲线减小幅度较小,且趋于平缓,即曲线有硬化趋势。且随温度的不断升高,应力峰值逐渐减小,表明高温引起土体内部胶结物质破坏,碳酸钙被分解,土样孔隙变大,土体内部损伤增多。

综上可知,本文所建损伤本构模型对变温条件下结构性黄土的拟合效果较好,总体趋势相同,能充分反映高温黄土在三轴试验下的应力-应变关系,模拟结构性黄土在不同温度下的变形破坏特征,更符合结构性黄土的损伤破坏规律。总体来说,本文所建立的统计损伤本构模型能够较为准确地描述西安地区黄土损伤变形的全过程。