基于ARIMA模型的涡轴发动机排气温度预测
2023-12-13包志安韩雅慧黄汉超
包志安,韩雅慧,黄汉超
(陆军航空兵学院,北京 101123)
0 引言
涡轴发动机是直升机的动力来源。发动机的剩余寿命是评估其健康状况的主要指标,保证足够的发动机剩余寿命对于保证直升机飞行安全与降低维护成本都具有十分重要的意义。不过,直接获取发动机的剩余寿命比较困难且耗费巨大,目前比较可靠的方式是通过监测发动机排气温度裕度的退化来间接获得发动机的剩余寿命。排气温度裕度(Exhaust Gas Temperature Margin,EGTM),是发动机的关键使用数据之一。EGTM是发动机做全功率起飞时,排气温度值(EGT)与手册规定的排气温度红线值(EGTred)之间的差值。当发动机的EGTM下降到阈值时,就需要进行维护[1]。
Yilmaz 等[2]在2009年根据多元线性回归分析的方法研究了排气温度与发动机运行参数(发动机净推力、燃油流量、增压比等)之间的关系。KUMAR等[3]在2015年通过自回归神经网络与滑动平均相结合的方法,进行排气温度的建模和预测。Lasheras等[4]在2019年提出了一种将ARIMA与SVM模型相结合的ARIMA-SVM混合模型来研究航空发动机的剩余使用寿命。Ahmed Z. AL-Garni等[5]在2018年提出了一种基于径向基函数(RBF)的人工神经网络算法。
任淑红等[6-8]在2009年、2010年、2011年相继提出了基于带漂移的布朗运动的排气温度预测模型,利用状态空间方法建立起时变性能退化模型,通过卡尔曼滤波方法对航空发动机的性能趋势进行预测。王华伟等[9]在2014年提出了基于竞争失效的航空发动机剩余寿命预测方法。皮骏等[10]在2019年利用果蝇算法对广义神经网络进行优化(IFOA-GRNN)。戴邵武等[11]在2020年提出了改进经验模态分解(EMD)与支持向量回归(SVR)结合的预测方法。孔晨亦等[12]在2020年提出了一种基于自编码器Autoencoder和时间卷积神经网络TCN的航空发动机排气温度裕度预测模型。玉兰[13]在2021年提出了基于DCNN-LightGBM的剩余寿命预测模型。王新刚等[14]在2021年提出了一种多元退化失效和突发失效之间相关竞争失效的可靠性评估方法。
本文将排气温度作为时间序列数据,从序列自身的相关性出发,揭示时间序列自身的发展趋势,以此达到通过自身历史数据来预测未来发展趋势的目标;通过排气温度的变化预测发动机的剩余寿命,保证发动机的工作安全。
1 数据预处理
1.1 数据采集
对于涡轴发动机而言,采集起飞EGT需要注意以下几点:
1)起飞阶段,EGT最高的点;
2)对应发动机扭矩最高点;
3)直升机过渡速度附近。
本文是在涡轴发动机的实际外场使用数据中获取EGTM,即在每个飞行场次中选取一条符合上述3点要求的数据作为该飞行场次的起飞EGT值,进一步获得了一段时间内的起飞EGT数据。
1.2 数据筛选
涡轴发动机的工作环境复杂,发动机上的传感器在参数记录过程中也可能出现故障或存在误差,造成发动机的外场使用数据中存在许多偏离正常值较多的、不合理的数据,需要进行剔除。本文采用线性回归的方式剔除偏离正常值较多的异常值。
数据采集后,首先进行线性拟合,绘制散点图与回归函数曲线如图1所示。
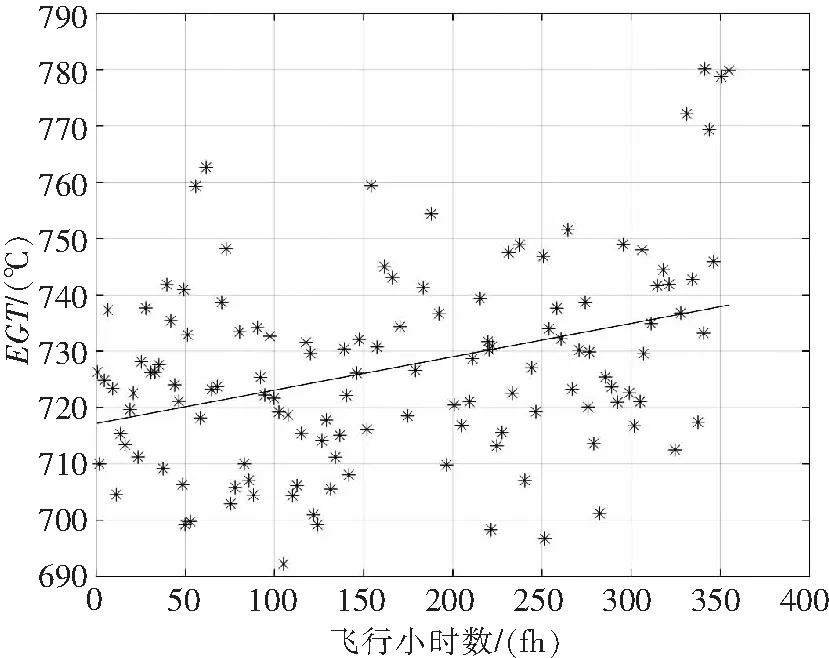
图1 1#发动机EGT数据散点图
在获得回归函数曲线后,进一步绘制其残差的95%置信区间(见图2),若残差值在置信区间以外,则能够判明该数据为异常数据。
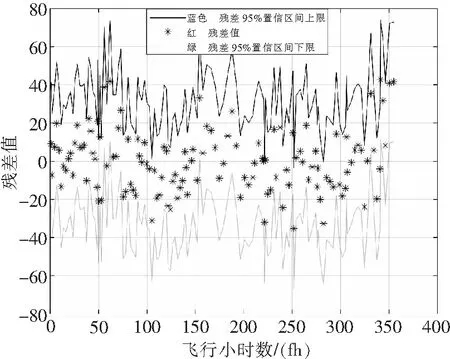
图2 1#发动机EGT数据残差区间
不过,从此图清晰地看出具体哪一个数据点的数据为异常数据还比较困难。为了更为直观地显示异常数据,进一步绘制残差图见图3。
在残差图中,红色部分对应的EGT数据为偏离正常值较远的异常数据,需要剔除[15-16]。
1.3 数据换算
在筛选获取到EGT数据后,需要进行排气温度换算,即将EGT数据换算到相同进口条件,以具有可比性。经查阅资料,有3种常用的换算方式:
1)ITTcor=ITT*288.15/(TO+273.15)
式中,ITTcor为换算的涡轮级间温度[17]。
式中,EGT*为换算值,TAT为大气温度[18]。
为选择合适的换算方式,本文选取1#发动机2019年至2020年大约350飞行小时的数据,通过上述三种方式进行换算并比较。图4与图5分别为发动机的原始EGT数据图与换算EGT数据图。
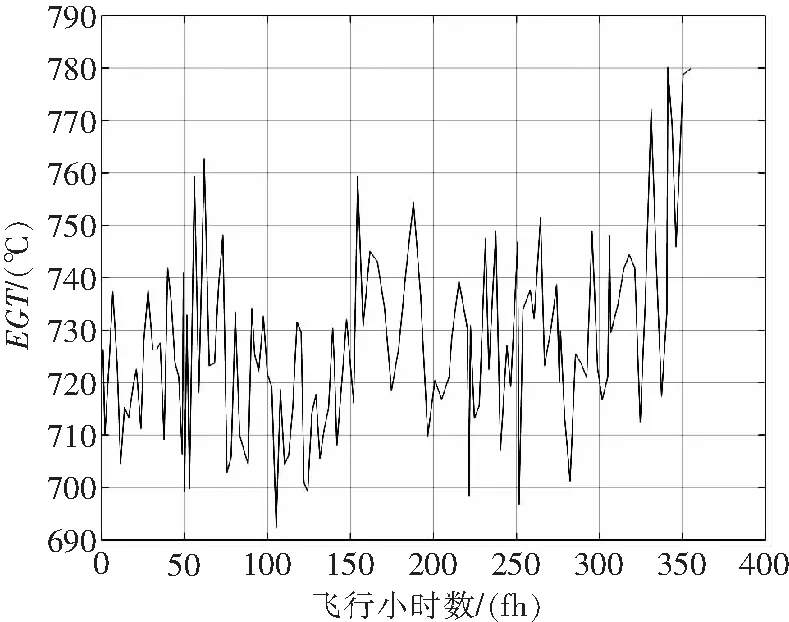
图4 1#发动机原始EGT数据图
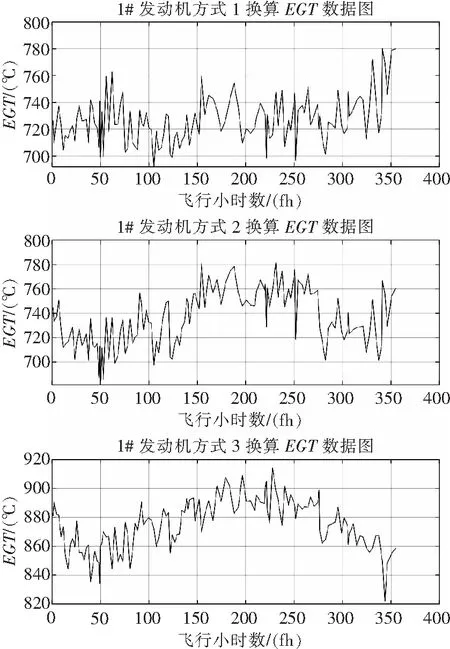
图5 1#发动机换算EGT数据图
结果显示,实际的EGT数据比较混乱,其退化趋势不明显。对比三种换算方式,有以下结论:
1)方式1换算EGT数据具有明显向上漂移的趋势,较好地拟合了发动机性能衰减的规律。
2)方式2与方式3换算EGT数据存在波动。
3)方式3换算EGT数据,总体排气温度值较高,且存在较大的向下漂移的趋势,不符合衰退规律。
为避免因数据数量过少、数据波动过大等原因造成换算方法选取不合适,本文增加了4台涡轴发动机外场使用数据,按50飞行小时进行切片,通过方式1与方式2进行EGT换算,进一步对比。结果如图6所示。
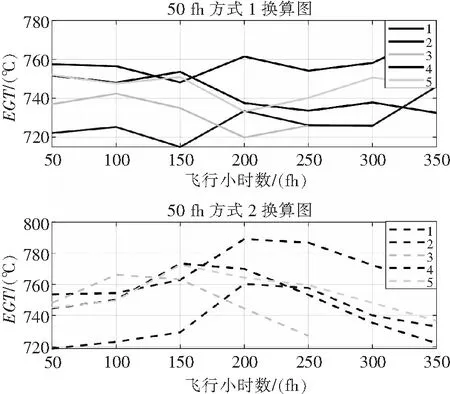
图6 两种方式EGT换算数据图
从图6数据中可以观察到以下几个特征:
1)方式1换算后的EGT数据,1#、2#两台发动机有明显的向上漂移的趋势,3#、4#、5#三台发动机略微向下漂移。
2)方式2转换后的EGT数据,5台发动机均显示出先升高后降低的趋势,EGT波动较大,不能够判定其变化趋势。
综上所述,方式2与方式3不能显示EGT的变化趋势,而方式1能够较好地拟合发动机的性能退化过程,所以本文选用方式1作为EGT的换算方法。
2 基于ARIMA模型的排气温度预测
2.1 ARIMA模型
AR模型,即自回归模型,是利用自身做回归变量来描述未来趋势的方法。
设时间序列{Xt},满足:
Xt=a0+a1Xt-1+…+apXt-p+εt
(1)
式中:εt为白噪声序列,a0,a1,…,ap是p+1个实数,并称此模型为p阶自回归模型,记为AR(p)模型。
MA模型,即滑动平均模型,可以看成是参数受某种限制的无穷阶AR模型,q阶MA模型定义为:
Xt=c0+εt-b1εt-1-…bqεt-q
(2)
式中:b1,b2,…,bq是滑动平均模型的参数,表征了每一个之前时刻的残差对当前时刻观测值的影响,q为阶数,并称此模型为q阶滑动平均模型,记为MA(q)模型。
ARIMA(p,d,q)称为差分自回归滑动平均模型。其中AR是表示的是自回归,p代表自回归项;MA表示的是滑动平均,q代表滑动平均项数;d表示的是时间序列成为平稳序列所需要差分的次数。ARIMA模型是在AR模型和MA模型的基础上进行组合得到的,是指将非平稳时间序列转化为平稳时间序列,然后仅对因变量Xt的滞后值以及随机误差项εt的现值和滞后值进行回归所建立的模型[20]。
2.2 平稳性检验与模型建立
平稳性检验的目的是检查时间序列数据是否具有稳定的分布特征,有助于检测出时间序列数据中的趋势,以便进行合理的分析和预测。一个时间序列模型的步骤一般遵循图7所示流程[20]。

图7 时间序列建模步骤图
第一步,平稳性检验。通常有ADF检验与PP检验两种。在确定数据序列具有平稳性后,再进一步对数据进行分析。如果数据整体不够平稳,则需要进行差分运算,得到平稳的数据。
第二步,AIC准则定阶。AIC准则,即最小信息准则,能够较为准确地确定出最适合模型的阶数。标准化的AIC准则函数如下:
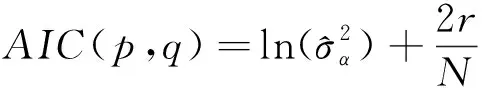
(3)

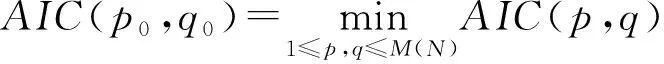
第三步,模型检验。方法为Ljung-BoxQ检验,用于判断建立的模型是否能够恰当地描述时间序列,实质上就是检验残差序列是否为白噪声序列,即拟合残差相中不再蕴含任何相关信息。
2.3 实例分析
本文选取文献[21]中的数据进行分析。发动机的原始EGTM数据序列如图8所示。
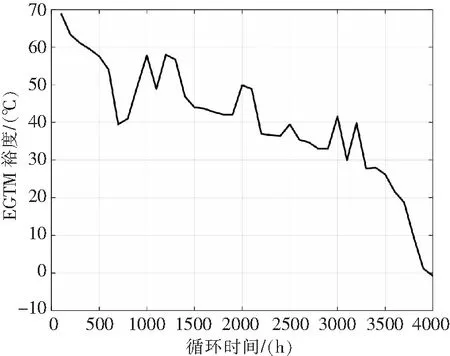
图8 原始EGTM数据序列图
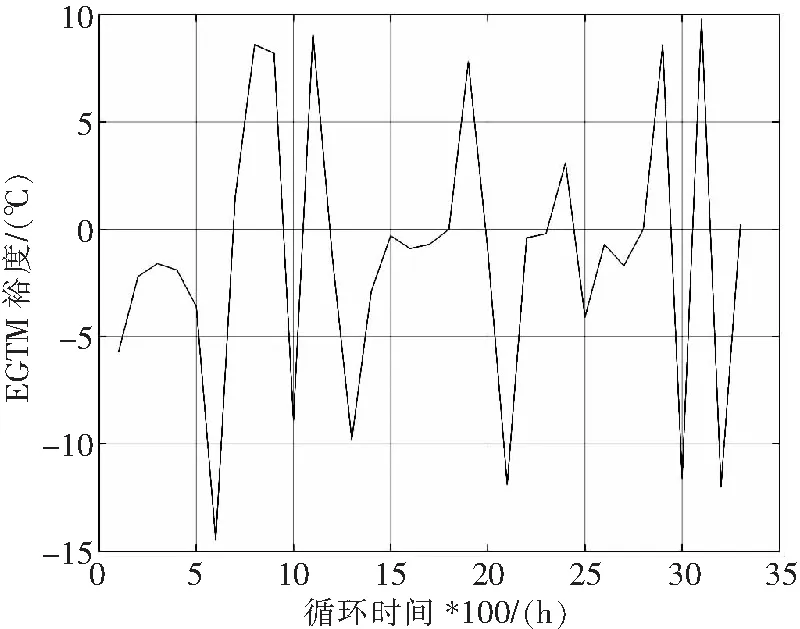
图9 一阶差分后EGTM数据序列图
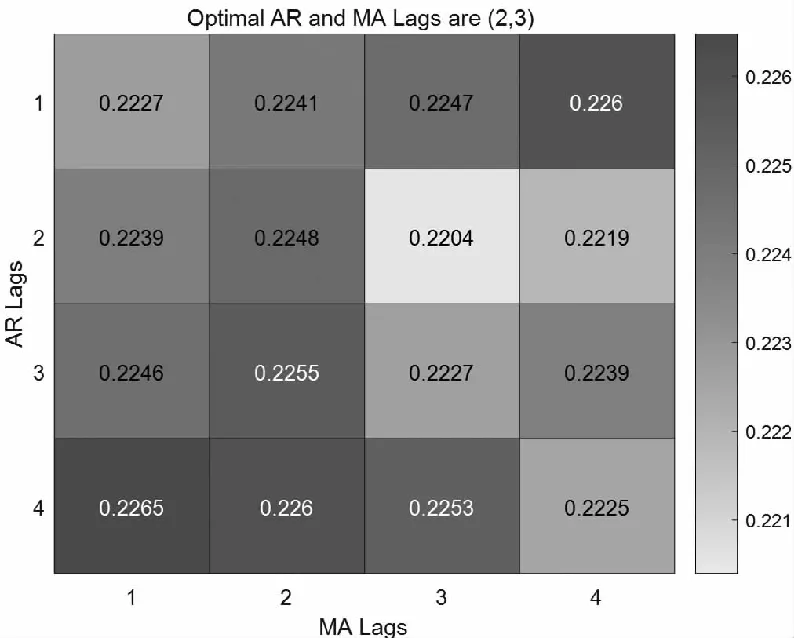
图10 AIC准则定阶分布图

图11 EGTM序列预测曲线
为了能够检验数据预测的准确度,在此把数据的前70%作为训练集,其后30%作为验证集。观察数据序列,可以看出其具有明显减小的趋势,不具有平稳性,因此进一步对数据进行一阶差分处理。
接下来,通过AIC准则进行模型拟合,确定最合适数据序列的模型阶数。为了更加直观地看出适合的模型阶数,绘制AIC准则定阶分布图。
根据数据结果,确定模型为ARIMA(2,1,3)。
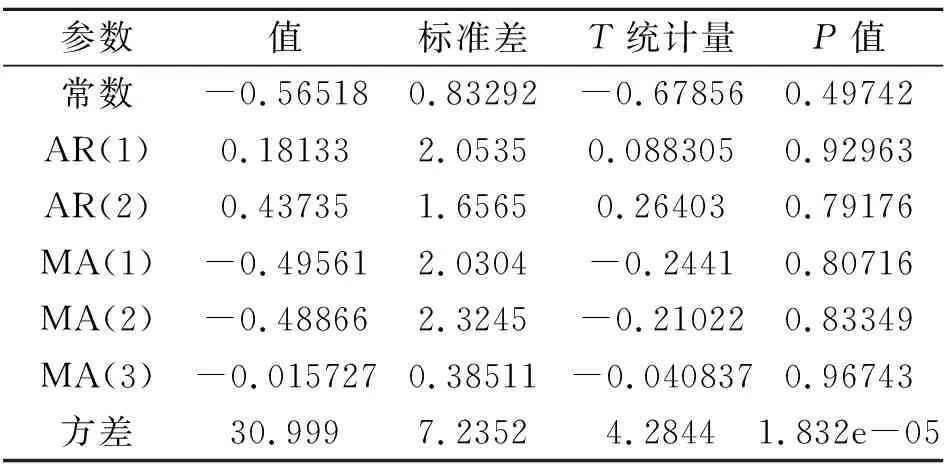
表1 模型参数表
从表中得到ARIMA(2,1,3)模型如下:
Xt=0.18133Xt-1+0.43735Xt-p+εt-
0.49561εt-1-0.48866εt-2-0.015727εt-3
(4)
继续检验残差是否具有相关性。从表2中可以看到hLBQ=0,因此残差不具有相关性,该模型的显著性符合要求。

表3 1#发动机模型参数表
最终依据模型,利用前70%数据进行建模预测,得到最终的预测结果。
分析结果得知,预测曲线的置信下限与EGTM阈值的交点与实际EGTM数据与EGTM阈值的交点几乎重合,证明了该模型的精度。该模型能够充分拟合发动机的退化过程并进行预测。
验证了模型精度后,选取1#发动机的退化数据进行预测分析。图12为原始EGTM数据序列图。
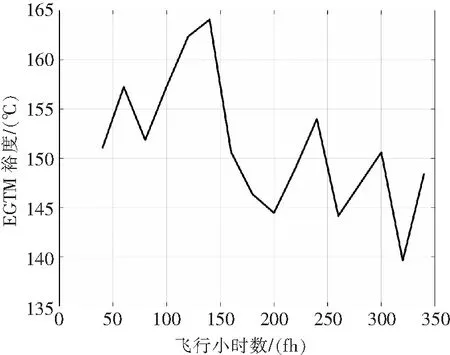
图12 1#发动机原始EGTM数据序列图

图13 一阶差分后EGTM数据序列图
通过观察,其趋势明显下降,不具有平稳性,需要进行差分处理。
运用AIC准则函数对差分处理后的数据进行定阶,在图14的定阶分布图中找到最合适的模型阶数,确定模型为ARIMA(2,1,2)。
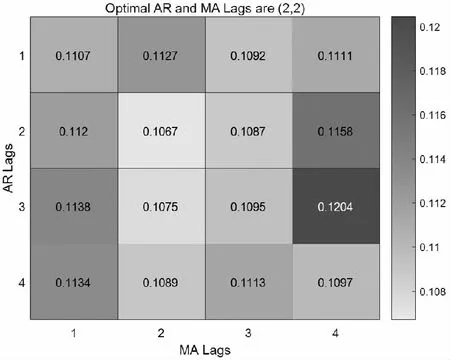
图14 1#发动机AIC准则定阶分布图
从表中得到ARIMA(2,1,2)模型如下:
Xt=0.94555Xt-1-0.80265Xt-p+
εt-2εt-1-0.99998εt-2
(5)
继续检验残差是否具有相关性。从表4中可以看到hLBQ=0,因此残差不具有相关性,该模型的显著性符合要求。

表4 模型显著性检验参数表
最终,依据该模型,进行EGTM的预测,得到预测曲线见图15。
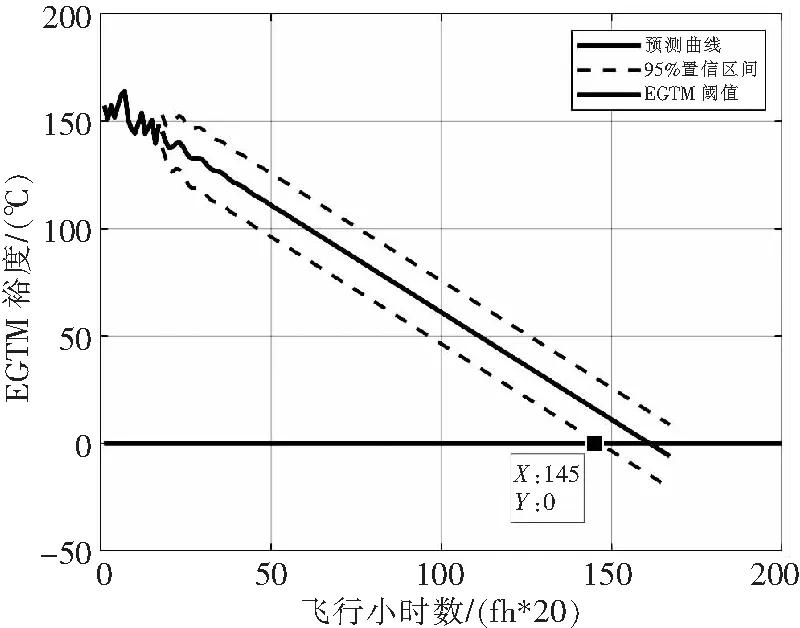
图15 1#发动机EGTM序列预测曲线
从预测结果来看,飞行小时数为2900小时的时刻,为发动机下发返厂的时刻。本台发动机装于本机之前的训练时间估计为300飞行小时,因此最终预测的下发时间为3200飞行小时。
3 结论
对于该发动机而言,翻修时间为3000小时,而经过模型估计的翻修时间为3200小时。分析结果得到以下结论:
1)发动机排气温度短期波动大,预测趋势精度较好。可以看出,发动机的实际排气温度值存在较大波动,在进行模型精度检验时显示出较好的拟合度。
2)统计飞行小时多于发动机使用时间。在飞参系统记录数据过程中,发动机起动前与发动机起动后一段时间统计在飞行小时内,但发动机实际已经处于关车状态。
3)低载荷训练可能延迟维修。直升机在日常训练过程中,大强度、超负荷的训练课目较少,不会对发动机造成过载,使得其实际使用寿命较规定翻修期限长一些。
