基于物理信息神经网络的Burgers-Fisher方程求解方法

徐健，朱海龙，朱江乐，李春忠

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

随着以数据为载体的智能时代的到来，数据驱动方法已经成功应用于多种科学和工程研究领域[1].这些领域的很多问题都可以被描述为某种微分方程模型，通常求解这些方程有理论解析解和数值逼近解2 种思路.然而，通过直接的理论推导获得解析解往往会因模型的复杂性而很难进行，如果对模型方程进行简化又会导致求解不够精确.数值逼近的求解方法，则需要构造各种类型的解结构进行拟合，方程的求解结果也往往会受到这些构造方法特性的制约，特别是在逆问题、复杂几何和高维空间等问题上面临着较多挑战[2].

如果可以从微分方程自身的特征出发，将表现方程特征的先验物理信息，以数据驱动的方式融合进求解微分方程的神经网络的训练中，促使神经网络逼近相应的方程特征，从而得到能够描述这些先验物理信息的微分方程解.这种求解微分方程的思路更加简单和直接，避免了模型简化和复杂构造带来的理论和误差问题，也提供了对方程物理信息的量化与认知.

基于物理信息的神经网络（physics-informed neural networks,PINN）是由Raissi 等[3]在原有人工神经网络求解微分方程基础上拓展出的深度学习算法框架.PINN 是由数据驱动的用于解决有监督学习任务的神经网络，能够在遵循训练数据样本分布规律的同时，得到符合微分方程所描述物理特征的方程解，从而适用于探索各类由微分方程表达的物理问题[4].PINN 相比于传统的神经网络，能够融合微分方程和物理问题的先验知识，在减少样本训练和提高模型泛化能力的同时，为神经网络提供某种程度的可解释性，从而在一定程度上打破神经网络的黑箱效应.

近年来，由于PINN 具有计算速度快，精度高，仅从数据角度出发就可以利用神经网络直接拟合物理问题的优点，发展非常迅速，也为微分方程的数值求解开辟了一条新的途径.很多学者利用PINN 对一些偏微分方程（partial differential equation，PDE）进行了研究，Lu 等[5]描述了PINN求解PDE 的一般性步骤.Lin 等[6]设计了两阶段PINN，在第2 阶段将守恒量测量引入均方差损失中，结合第1 阶段的PINN 来训练神经网络，从而模拟Sawada-Kotera 和Boussinesq-Burgers 可积方程的局域波解.Lin 等[7]还研究了基于非线性PDE 解的初始和边界数据，利用Miura 变换和PINN 获得演化方程的数据驱动解，从而克服了基于隐式表达式求解的困难，并在KdV-mKdV 方程的实验中发现了新的局部化波解：散焦mKdV 方程的kink-bell 类型解.Miao 等[8]将PINN 应用于高维系统，以解决具有2N+1 个超平面边界的N+1 维初始边界问题，并应用在2+1 维可积Kadomtsev-Petviashvili（KP）方程和3+1 维约化KP 方程中，再现了这些可积系统的经典解.Pu 等[9]从神经元局部自适应激活函数和L2 范数的参数正则化2 个角度来改进PINN，并在Yajima-Oikawa（YO）系统的正向问题中恢复了3 种不同初始边值条件下的矢量流氓波（RW），还利用不同噪声强度的训练数据研究了YO 系统的反向问题.

目前，PINN 的研究多关注将数学特性和数学方法加持到求解PDE 的过程中，对PINN 中物理信息如何影响神经网络训练的分析较少，对求解PDE 时PINN 的微观表现，以及影响PINN 工程化应用的神经网络规模在迭代次数和时间上对求解效果影响的讨论也较少.本研究通过将方程的物理信息分为规律信息和数值信息2 类，来分析从“physics-informed,PI”到“neural networks,NN”的数据驱动过程，给出PINN 求解PDE 的可解释性，并探索这2 种信息对PINN 求解PDE 的影响.同时，利用PINN 求解Burgers-Fisher 方程，在数值实验中分析PINN 求解方程的微观和宏观误差与求解稳定性，以及2 类信息对刻画方程的神经网络训练的影响，讨论神经网络规模在迭代次数和时间上对求解方程效果的影响.

1 数学方程模型

微分方程可以描述众多科学和工程领域的物理问题，一些经典的方程已经成为相关问题的基础解决理论和分析方法.Burgers-Fisher 方程可以描述各类反应系统，如对流传导和扩散传播中的非线性特征等，因此已经在物理、化学、生物、金融和社会学领域有了广泛的应用，具有较高的科学研究和工程应用价值[10].广义Burgers-Fisher 方程被描述为如下形式的控制方程[11]：

式中：x为空间变量，x∈[0,1.0] ；t为时间变量，t≥0；该方程描述了反应系统中的耗散转移和平流协调；u为关于x和t的函数；ut为u关于t的一阶导数，刻画了物理量的时间变化率；ux和uxx分别表示u关于x的一阶和二阶导数，描绘了物理量在不同位置的差异程度和变化情况；参数α、β 和δ为具体常数.不同的 α、β 和 δ 数值情况可以表达不同类型的方程，例如，当 δ=1、α=0、β=0和 α=β=0时，式（1）分别为Fisher 方程、Burgers 方程和线性扩散方程，因此对广义Burgers-Fisher 方程的研究是非常有意义的.很多研究已经从理论上给出了方程解析解[12-13]，具体形式如下：

式（1）概括了方程描述的物理量u须遵循的整体形态，即当x∈[0,1.0]，t≥0 时，变量x和t的二元函数u体现了式（1）表现的方程规律，是方程的内部条件物理信息.当t=0 时，可以得到方程的初始条件物理信息；当x=0，1.0 时，则体现了方程的边界条件物理信息.以上各类信息表达式如下：

2 求解Burgers-Fisher 方程相关方法

除了从理论上得到广义Burgers-Fisher 方程的解析解（式（2））外，很多文献也都给出了各种数值求解方法，例如传统求解PDE 的各种谱方法，包括Javidi[14]提出的谱配置法、Zhao 等[15]提出的伪谱法、Golbabai 等[16]提出的谱域分解法等.近年来，也有很多学者提出各种求解方程的数值方法，Alotaibi 等[17]利用改进的Adomian 分解法（Adomian decomposition method，ADM）和同伦摄动法（Homotopy perturbation method，HPM）结合Yang 变换来研究和分析广义Burgers-Fisher 方程.潘悦悦等[10]基于交替分段技术，将古典显式格式与隐式格式和Crank-Nicolson（C-N）格式恰当组合，提出求解Burgers-Fisher 方程的改进交替分段Crank-Nicolson（improved alternate segment C-N，IASC-N）并行差分方法，并从理论上分析了IASC-N 并行差分解的存在唯一性、稳定性和收敛性.赵国忠等[18]构造了一类局部间断Petrov-Galerkin 方法求解Burgers-Fisher 方程，并针对2 个特殊的案例进行包括稳定性在内的数值分析.Singa 等[19]将四阶B 样条配置方法应用在Burgers-Fisher 方程的数值求解中，并证明了这种方法的收敛性，以及利用傅里叶级数分析了这种数值求解方法的稳定性.

传统的谱方法和有限差分方法都须对方程进行离散化和区域剖分，其他的数值求解方法也都要利用数学理论和设计特殊的结构来拟合微分方程，求解过程相对较复杂.PINN 目前虽然在计算精度方面还不如一些传统的算法，但是可以直接从方程的特征入手，将物理信息通过采样的方式数据化，来驱动训练神经网络，从而有效地避免方程中的各类数学构造带来的复杂性，对解决高维问题和反问题有较大的优势，而且求解效率相对于传统算法也具有一定的优势.因此，本研究以Burgers-Fisher 方程为例，采用PINN 建立数值化求解方程的神经网络，通过采样方程的物理信息数据来训练该神经网络逼近方程的解，并进一步探索不同的方程物理信息对神经网络训练的影响，以及神经网络规模对方程求解的影响.

3 基于物理信息的神经网络求解方法

3.1 PINN 求解过程及解释性

科学和工程领域的物理问题，可以抽象成以各类条件的先验物理信息为特征表现形式的微分方程，通过采样可以获得相应数据信息.PINN 基于这些数据信息，以数据驱动的方式训练神经网络，以此将这些物理信息融合进神经网络中，得到微分方程的数值解[20].因此，PINN 将微分方程的求解问题转换为训练神经网络逼近方程物理信息的优化问题，并在一定程度上解释了神经网络的物理意义[21]，整体思路如图1 所示.

图1 PINN 求解物理问题的示意图Fig.1 Schematic of PINN dealing with physical problems

本研究认为PINN 包含了物理信息“PI”和神经网络“NN”，体现了可认知和可测量2 个方面.可认知表现为方程的物理信息提供了神经网络需要逼近的目标，从而为神经网络提供了可解释性；可测量则是指对物理信息的数值化测度，即通过模拟、计算和实验等方式获得体现方程物理信息的数据，最终以数据驱动方式训练神经网络实现从“NN”向“PI”的逼近.具体逻辑关系如图2所示.

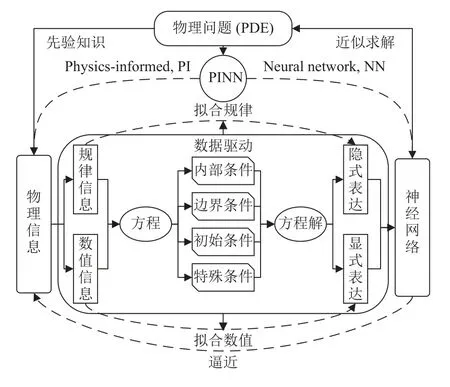
图2 PINN 求解PDE 的逻辑解释Fig.2 Logical explanation of solving PDE with PINN

PDE 的物理信息可以分为规律信息和数值信息2 类，具体表现为描述微分方程特征的内部条件、初始条件和边界条件，以及方程的某些特殊条件.规律信息是方程解的隐式表达，如由式（1）表示的方程内部条件或者其他体现方程规律的特殊条件，数值信息是方程解的显式表达，如由式（3）～（5）表示的方程初始条件、边界条件或者实验观测结果体现的特殊数值条件.通过在这些规律信息和数值信息上的采样获得带有这些信息的数据，以拟合方程解的规律和数值为目标，进行数据驱动训练神经网络，使得神经网络逼近PDE 的这些物理信息，从而获得体现PDE 解的神经网络，最终利用这个神经网络来近似计算PDE 的所有数值解.

方程的规律信息和数值信息是实现神经网络逼近方程物理信息的依据，可以通过设置不同的训练采样平衡度和训练强度平衡度，来控制这2 种信息对神经网络训练的影响.数据采样平衡度体现为在这2 类信息上的不同采样规模，训练强度平衡度体现为这2 类信息对训练神经网络的影响权重之比.

3.2 PINN求解Burgers-Fisher方程

根据以上论述，基于Lu 等[5]提出的一般性PINN 求解PDE 的步骤，Burgers-Fisher 方程求解过程可以表现为如图3 所示.将方程的物理信息分为由式（1）体现的方程内部条件规律信息，以及由式（3）～（5）体现的方程初始条件和边界条件数值信息.构建一个在参数空间 Θ 下的神经网络来描述方程的解，通过将这个解的结果与2 种信息结合来计算神经网络拟合物理信息的损失.即在训练采样平衡度下获得不同条件的训练数据，依据训练强度平衡度构建基于不同条件的综合信息损失，通过多次训练迭代实现神经网络逼近方程的物理信息，从而得到在神经网络参数空间 Θ 下使得综合信息损失最小的Burgers-Fisher 方程解u(x,t|θ)，θ∈Θ，即最贴近方程物理信息的神经网络.因此，这种将方程的规律信息和数值信息融合到神经网络中的方式，部分提供了神经网络的可解释性，也就是神经网络的综合信息损失体现为方程2 种信息的满足程度，也就是神经网络能够逼近方程物理信息的程度.

图3 PINN 求解Burgers-Fisher 方程过程示意图Fig.3 Schematic of PINN solving Burgers-Fisher equation

整个过程具体表现如下.创建2 阶段的神经网络，在第1 阶段设计由方程的2 个变量x和t作为输入，以方程解u(x,t|θ) 作为输出，在参数空间Θ下的神经网络.第2 阶段利用方程解u(x,t|θ) 结合方程的2 类物理信息：规律信息（内部条件）和数值信息（初始条件、边界条件），构建基于不同条件的神经网络综合信息损失函数L(θ|ω,τ)：

式中：LI、LIni、LB0和LB1分别为方程的内部条件信息损失、t=0 时的初始条件信息损失、x=0 时的边界条件信息损失和x=1.0 时的边界条件信息损失；ωI、ωIni、ωB0和 ωB1为这些条件信息损失对神经网络综合信息损失的影响权重，体现了不同条件的训练强度平衡度；一阶微分ut和ux，二阶微分uxx，以及零阶微分u自身，都可以在神经网络反向传播时，通过相应训练数据 τ（包括内部条件训练数据 τI、初始条件训练数据 τIni、2 种边界条件训练数据 τB0和 τB1）的梯度计算获得.

在物理信息上采样获得的训练数据 τ，可以将方程的规律信息和数值信息数据化，体现了不同条件的训练采样平衡度.以此训练神经网络得到使得综合信息损失函数L(θ|ω) 达到最小的最优参数 θ*=argmin {L(θ|ω)}，从而获得用神经网络体现的逼近方程物理信息的微分方程解u(x,t|θ*).

综上所述，PINN 求解Burgers-Fisher 方程的具体步骤如下.

1）设置各类参数创建一个在参数空间 Θ 下描述方程解u(x,t|θ∈Θ) 的神经网络；

2）综合方程的内部条件规律信息，初始条件和边界条件数值信息，依据训练强度平衡度，设置不同条件信息损失的影响权重，构建神经网络的综合信息损失函数L(θ|ω,τ) ；

3）依据训练采样平衡度，在方程内部条件、初始条件和边界条件上进行数据采样，获得相应训练数据 τI、τIni、τB0和 τB1；

4）利用步骤3）的采样数据训练神经网络，获得实现步骤2）中综合信息损失函数最小化的参数 θ*，从而得到微分方程解u(x,t|θ*).

4 数值实验

在Windows 11 系统下，基于PyTorch 深度学习框架编写实验代码脚本，在处理器为Core i7-10700K，16 G 内存的硬件条件下的Visual Studio Code 1.77.1 上运行以下实验.

4.1 不同方程参数的求解测试

为了验证PINN 求解Burgers-Fisher 方程的具体效果，依照已有文献设置方程的参数为情况1（α=β=0.1 和 δ=1.0）和情况 2（α=β=0.5 和δ=2.0）[11].构造4 个隐藏中间层、每层50 个神经元的神经网络，采用tanh 作为激活函数[3]，设置各种条件的信息损失权重为1.0，即让规律信息和数值信息在训练强度上达到平衡.

在神经网络训练阶段，在方程内部条件（x∈(0,1.0)，t∈(0,10.0)）上随机采样3 000 个训练数据坐标，分别在初始条件（t=0）和2 个边界条件（x=0 和x=1.0）上随机采样1 000 个训练数据坐标，让规律信息与数值信息在训练采样上也达到平衡.设置神经网络的训练迭代次数为1 000，对2 种参数情况下的Burgers-Fisher 方程进行神经网络训练.

在神经网络测试阶段，进行网格化采样（分别在x∈[0,1.0] 和t∈[0,10.0] 上等间距Δx=0.1 和Δt=1.0）获得测试数据坐标.利用训练得到的神经网络计算在这些坐标上的方程解的预测值，与式（2）得到的方程解的精确值进行对比.首先，选取网格对角线上的测试数据坐标进行对比，如表1所示.表中，RPre、RExa和EAbs分别表示方程解的预测值、精确值和两者的绝对误差.可以看出，在2 种参数情况下，这些特殊测试数据上的预测值和精确值的绝对误差较小，说明预测值和精确值较接近.其次，总体上所有测试数据在参数情况1 和参数情况2 下的预测绝对误差均值分别为1.668 3×10-3和4.983 4×10-4，标准差分别为1.628 6×10-3和5.224 1×10-4，说明PINN 在网格化采样坐标上可以较好地求解方程，解的稳定性也较高.

表1 网格采样中对角线数据坐标的预测结果Tab.1 Prediction results of diagonal data coordinates in grid sampling

为了绘制方程的图像，采用已有文献的2 种方程参数设置[11]，在x∈[0,1.0] 和t∈[0,20.0] 内等均距获取测试数据坐标，利用上面训练得到的神经网络计算方程解如图4 所示，与文献得到的图形一致.因此，PINN 在这2 种方程参数情况下，训练得到的神经网络都可以较好地逼近方程的精确解.

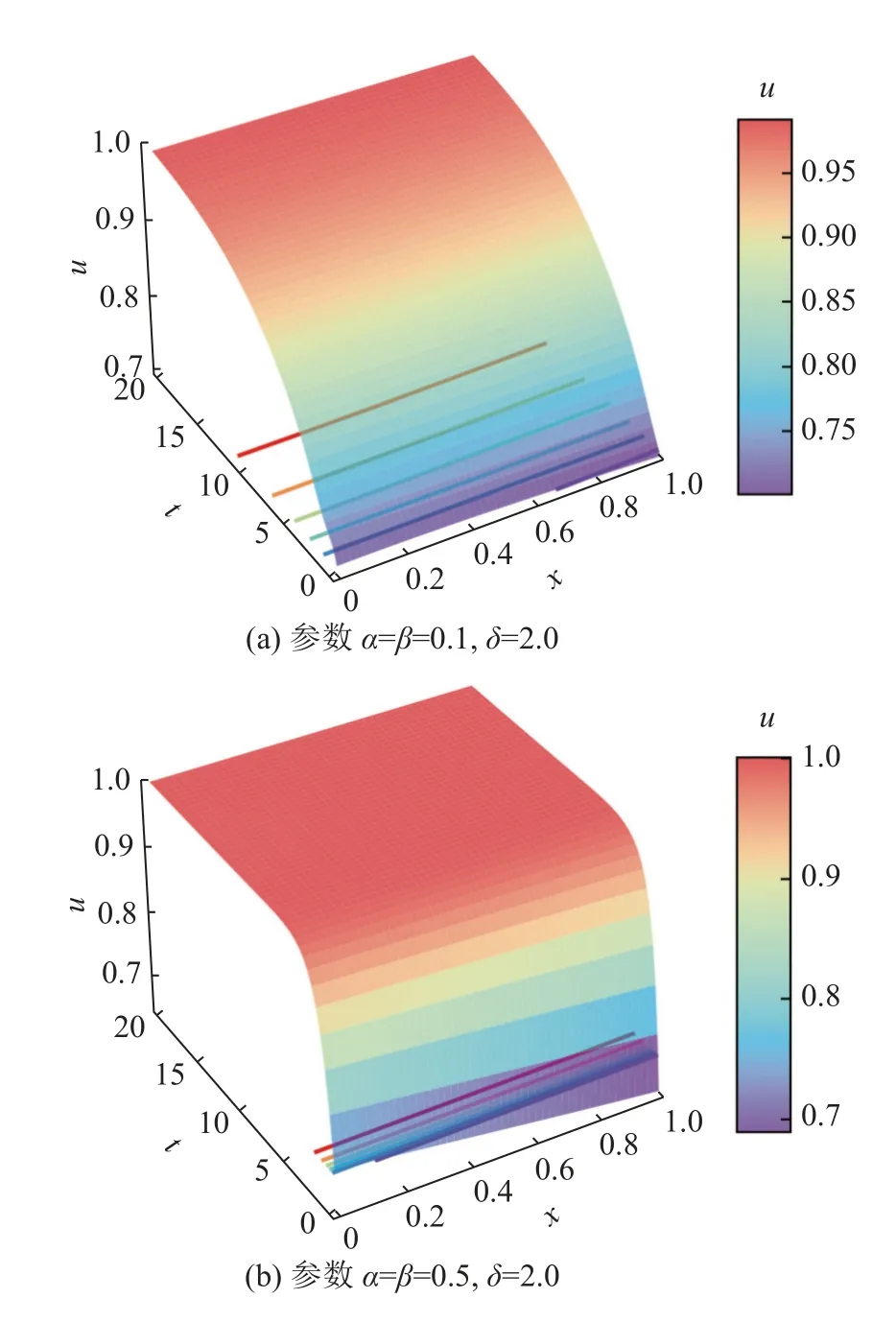
图4 2 种参数情况下的方程解的三维曲面图Fig.4 Three-dimensional surface of equation solution on two cases

4.2 不同迭代次数的求解测试

为了考察神经网络训练迭代次数对PINN 求解方程的影响.设置方程参数为 α=β=0.1，δ=2.0，在x∈[0,1.0] 和t∈[0,20.0] 的方程内部条件、初始条件和边界条件上分别进行规模分别为3 000、1 000、1 000、1 000 的随机训练数据采样，以及相同规模的随机测试数据采样，设置与4.1 节相同的神经网络参数.随着神经网络训练迭代次数e的变化，测试数据坐标上解的预测值与精确值的绝对误差的最大值EMax、最小值EMin、均值EMea和标准差ESta变化趋势如图5 所示.可以看出，随着神经网络训练迭代次数的增加，PINN 求解方程的效果会越来越好，这种效果的提升在训练初期较快，但随着训练次数逐渐增加提升会越来越小.具体表现为，在宏观上所有测试数据的预测绝对误差的均值随着训练次数增加是在降低的，而由绝对误差的标准差体现的预测稳定性也是提高的，但幅度都在减少.在微观上所有测试数据的绝对误差最大值和最小值总体上也呈现随迭代次数增加而减少的趋势，但预测误差最小值在个别地方出现了微小上升，这是由于测试样本在较小数值时出现的波动，并不影响总体上PINN 的预测精度和稳定性随迭代次数增加而提高的结论.

图5 绝对误差随神经网络训练迭代次数的变化Fig.5 Change of absolute error with number of epochs of neural network training

4.3 不同神经网络规模的求解测试

为了考察神经网络规模对PINN 求解方程的影响，采用与4.2 节相同的方程参数，以及训练和测试数据生成策略.网络规模SNet由不同的隐藏层数和每层上的神经元个数刻画，例如SNet为“L2N40”表示2 个隐藏层，每层40 个神经元.分别设置神经网络中间隐藏层数为2、4、6 和神经元个数为10、20、40 共9 种网络规模[3]，设定神经网络训练迭代次数为1 000，统计测试数据的预测值与精确解的绝对误差情况，以及训练时间TTim如表2 所示.可以看出，在同等层数条件下，随着神经元个数的增加，或者同等神经元个数条件下，随着网络层数的增加，宏观上的预测值与精确值的绝对误差均值和标准差都在下降.微观上所有测试数据的绝对误差最大值和最小值，总体上也是随着神经网络规模的增加而下降的.说明增加神经网络的复杂度可以提高方程解的预测精度和稳定性，即更高维的神经网络可以更好地拟合方程.

表2 固定迭代次数下预测值绝对误差随神经网络规模变化的描述性统计Tab.2 Descriptive statistic of absolute error of predicted values with scale of neural networks under a fixed epoch

从神经网络的训练时间来看，网络复杂度的增加虽然可以提升方程的求解精度和稳定性，但是也增加了训练时间.在一些工程应用领域，神经网络的训练时间是重要的考虑指标.因此，本研究固定神经网络训练时间为10 s，来对比不同网络规模下的求解效果和网络训练次数TNum，如表3 所示.可以看出，当固定神经网络训练时间时，在同等网络层数和神经元个数条件下，随着神经网络维度的增加，宏观上的预测值与精确值的绝对误差均值和标准差不是一直降低的，说明预测的精度和稳定性并非一直增加.在微观上绝对误差最大值和最小值也显示出相同的结果.这是因为越高维度的神经网络复杂性越高，训练速度就越慢，在同等时间下训练次数就越少（见表3的训练次数），根据4.2 节的结论，迭代次数越少，预测的精度和稳定性越低.

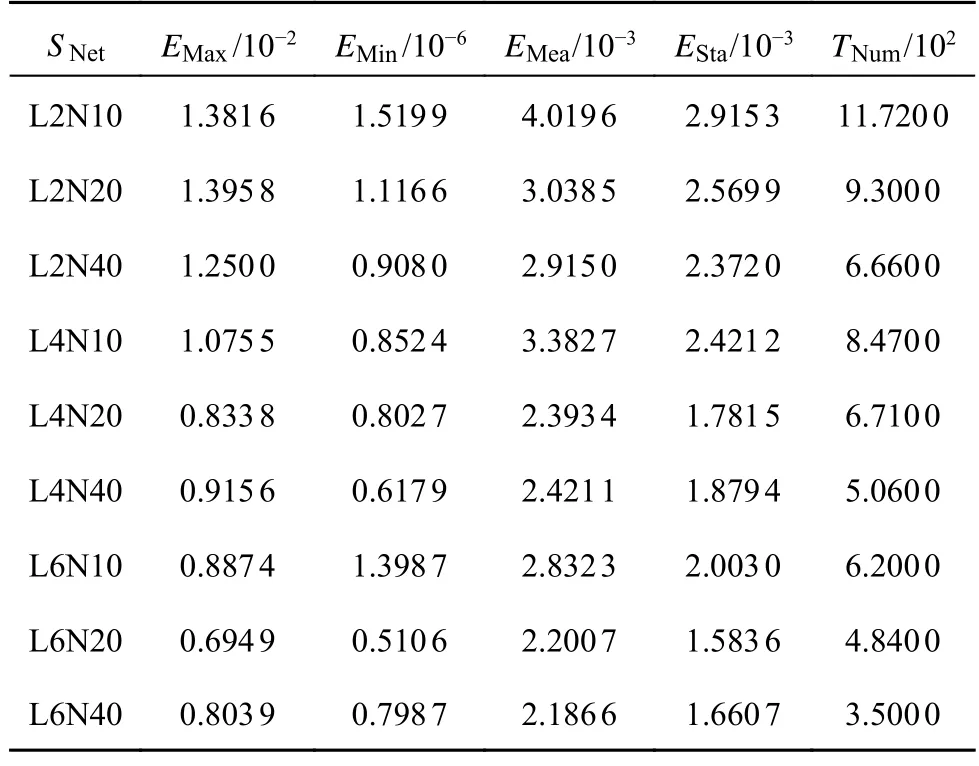
表3 固定训练时间下预测值绝对误差随神经网络规模变化的描述性统计Tab.3 Descriptive statistic of absolute error of predicted values with scale of neural networks under a fixed training time

总结来说，神经网络规模的增加可以提高求解效果，但在须考虑训练时间的工程应用中，神经网络规模的提升又会减少训练次数，从而降低求解效果.因此，在确定的训练时间下，如何选择合适的神经网络规模来提高方程求解效果，就存在需要优化博弈的选择，这是一个值得探索的方向.

4.4 不同规律信息与数值信息平衡度的求解测试

为了考察不同的规律信息与数值信息平衡度对PINN 求解方程的影响，设置具有4 个隐藏层、每层20 个神经元的神经网络，并采用与4.2 节相同的方程参数，固定每次神经网络的训练迭代的次数为1 000 次.

根据3.1 节的论述，方程的物理信息分为规律信息和数值信息，而这2 种信息对神经网络训练的控制，又是通过训练采样平衡度和训练强度平衡度来体现的.

对于训练采样平衡度BSam，在体现方程规律信息的内部条件上分别随机生成3 000、6 000、9 000 个训练采样数据，结合在体现方程数值信息的1 个初始条件和2 个边界条件上分别随机生成的1 000、2000 和3 000 个训练采样数据，共得到9 种不同规模的训练数据采样.例如，BSam为“6-2”表示在内部条件上进行6 000 个随机采样，在边界条件和初始条件上都进行2 000 个随机采样.

为了全面分析2 种信息对求解方程的影响，对体现规律信息的方程内部（x∈(0,1.0) 和t∈(0,20.0)上随机生成3 000 个测试数据）、体现数值信息的方程边缘（在边界条件和初始条件上都随机生成1 000 个测试数据）、体现2 类信息的方程整体（前面方程内部和方程边缘获取的所有测试数据）都进行测试，统计测试数据的预测值与精确值的绝对误差的相关情况，如表4 所示.可以看出，只采用方程的规律信息，即只利用方程的内部采样数据来训练神经网络，从而预测处于方程内部和方程边缘的解是完全不可行的.同时采用方程的规律信息和数值信息进行神经网络训练，不论在方程内部、方程边缘还是方程整体，得到的预测结果在同等采样数据规模下都是最好的.这是因为Burgers-Fisher 方程内部函数值波动较小，而神经网络如果不借助x=0 和x=1.0 的2 个边界条件的数值信息，会陷入方程的零解情况.说明边缘的数值信息对于PINN 求解Burgers-Fisher方程是非常重要的，结合规律信息和数值信息来指导神经网络训练，可以更好地得到逼近方程物理信息的神经网络.另外，也可以发现如果只采用方程的数值信息，即只利用方程的边界条件、初始条件的采样数据来训练神经网络，得到的结果也可以实现对方程解的预测.而且如果只求解方程的边缘位置，这种只进行边缘采样得到数值信息来训练的神经网络反而有时能得到更好的结果.另外，值得说明的是，随着采样规模的增加，不论是只采用规律信息还是数值信息，或者两者的结合都能够提高神经网络求解方程的效果，这是因为更多的数据采样提供了神经网络更多的方程信息.

对于训练强度平衡度BInt，在方程的内部条件、2 个边界条件、1 个初始条件上分别随机采样6 000、2 000、2 000 和2 000 个数据样本.即在训练采样达到平衡的前提下，设置7 种规律信息和数值信息的训练强度平衡度，例如，BInt为“10∶1”表示在训练神经网络时，体现方程规律信息的内部条件训练权重 ωI=10，而 ωIni、ωB0和 ωB1体现方程数值信息的边界和初始条件训练权重都为1.同样采用前面的参数设置和测试数据进行实验，统计在这7 种训练强度平衡度下，训练得到的神经网络在方程内部、方程边缘和方程整体上的预测值与精确值的绝对误差情况，如表5 所示.可以看出，与1∶1 的规律信息和数值信息平衡状态相比，增加规律信息的训练强度，所得到的神经网络一开始在方程内部、边缘和整体上都提高了求解精度和稳定性，但随着强度的继续增加，规律信息越来越多占据神经网络训练的主要部分，训练效果反而越来越差，这与表4 中只对规律信息采样来训练神经网络得到的结论是一致的.另外，增加数值信息强度的神经网络训练，也呈现出类似的实验效果，即方程的求解精度和稳定性随着单方面信息强度的增加呈现先提高后降低的情况，这也从训练强度的角度验证了表4体现的相关结论.说明规律信息和数值信息的训练强度需要达到平衡才能得到最好的求解效果，在表5 中这种平衡表现为1∶50 的平衡度.

由于Burgers-Fisher 方程的内部较为平整，没有复杂的规律变化，因此方程初始条件和边界条件的数值信息会对神经网络的训练起到更大的促进作用，但如果是求解方程内部有更多变化的微分方程时，规律信息则会起到更大的作用.

综上，在采用PINN 求解微分方程时，要使用适当的微分方程规律信息和数值信息平衡度来训练神经网络，这种平衡度可以从训练采样和训练强度2 种角度来实现，并根据所要求解的方程类型，进行具体设置.

5 结论

（1）从偏微分方程的物理信息数据驱动和神经网络可解释性的角度，阐释了PINN 从“PI”到“NN”的求解过程.

（2）将PDE 的物理信息分为微分方程的隐式规律信息和显示数值信息2 类，并从训练采样平衡度和训练强度平衡度2 个方面，设计神经网络的训练采样方式，以及构建神经网络的综合信息损失函数，从而控制2 类信息对神经网络训练的影响.

（3）提供了Burgers-Fisher 方程利用PINN 进行数值求解方法，通过数值实验发现，PINN 不论在微观上的方程解的最大误差和最小误差，还是宏观上的方程解的误差均值和标准差上都体现了较好的求解精度和稳定性；随着迭代次数的增加，PINN 求解方程的效果会越来越好；虽然神经网络规模的增加可以提高方程解的求解效果，但是也增加了每次训练的时间，因此固定训练时间下的神经网络规模存在最优博弈选择.只用规律信息训练神经网络无法实现对Burgers-Fisher 方程的求解，而加入数值信息训练的神经网络可以较好地求解方程.规律信息和数值信息可以通过训练采样和设置训练强度进行平衡.当这2 种信息达到一定的平衡度时，训练得到的神经网络求解方程的效果最好.

有待进一步研究的问题如下：

（1）依据微分方程的不同类型物理信息以及求解位置来设置规律信息和数值信息的平衡度，以达到更好的神经网络训练.

（2）在一些工程应用领域，在确定的神经网络训练时间下，如何设置PINN 的神经网络规模，以权衡由网络复杂度提升带来的求解精度提高和由训练次数减少带来的求解精度降低.

（3）由于微分方程的复杂性，很多方程存在多解或者零解，如何利用PINN 求解多解问题和避免零解带来的干扰.

（4）由于现实中很多物理问题可以通过实验之类的方法获得测量数据，如何将这些特殊条件下的数值信息融入神经网络的训练.

（5）由于现实中的工程问题往往规模较大，而PINN 方法的主要限制之一是其高维优化的高计算成本，虽然该问题可以通过采用域分解方法[22]进行处理，但是如何提高PINN 对大型问题的求解效率也是值得研究的.