深部高应力巷道控制机理

詹 平,孟海燕

(潞安集团 司马煤业公司,山西 长治 047105)

近年来,全球市场对能源的需求激增,煤炭产量屡创新高。浅部煤炭资源的开采已无法满足我国日益增长的能源需求,煤炭开采逐渐向深部发展[1]。据调查,我国已探明超千米的煤矿资源储量占49%.然而开采深度的增加,也使得深部巷道的稳定性难以控制[2-3]。深部巷道具有高地应力、高地温、复杂地质构造、围岩强度低、强流变、强采动等特点[4],这对煤炭资源的安全高效开采构成了严重威胁。研究深部巷道的变形破坏机理对深部巷道的稳定性控制至关重要[5]。

当前学者们对深部巷道的稳定性控制做了大量的研究,左键平等[6]研究了巷道的梯度破坏机理,并发现随着深度的增加应力梯度越来越明显。黄万朋等[7]研究了深部巷道的非对称变形机理,认为高应力作用下,不同性质围岩的蠕变差值是导致巷道非对称变形的主要因素。靖洪文等[8]以松动圈理论为核心,对巷道围岩进行分类,并提出相应的控制措施。当前对深部巷道的变形和破坏机理的研究还不足。只有对深部巷道的变形破坏机理开展深入研究,对症下药,才能更有效地控制深部巷道的稳定。本文采用理论分析和数值模拟的方法,研究了深部巷道塑性区的变化规律,并分析了支护强度、围岩力学参数等因素对深部巷道塑性区半径的影响。

1 深部巷道塑性区半径理论分析

对深部巷道围岩塑性区进行分析,将巷道进行如下简化。巷道形状简化为轴对称的圆形巷道;围岩为各向同性和均质;不考虑巷道的蠕变效应。巷道的开挖半径为r、p为原岩应力,C和φ分别为围岩的内聚力和内摩擦角。μ为围岩的泊松比,E和σc分别为围岩的弹性模量和抗压强度,k为侧压力系数,η为剪胀梯度。巷道的塑性区半径和位移分别为R和u.见图1.

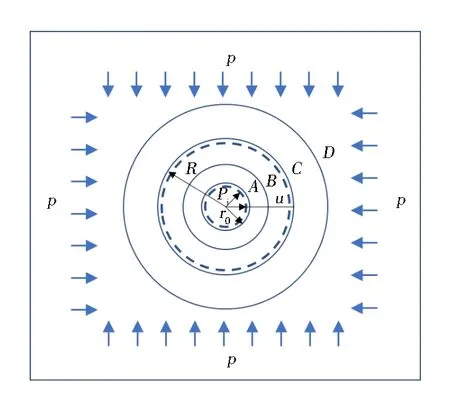
图1 圆形巷道的塑性区分布

(1)

(2)

(3)

式(1)和式(2)分别为巷道塑性区半径和巷道位移。根据上式可知深部巷道塑性区半径和巷道位移大小受到多个因素的影响。其中内因主要为围岩的物理力学性质、支护体强度、巷道半径。外因主要包括地应力大小、侧压力系数等因素。将某矿深部巷道的实际参数代入到公式中。其中R=2.4 m,p=30 MPa,η=2,σc=48 MPa,E=5 000 MPa.

图2显示出巷道塑性区半径与围岩黏聚力、内摩擦角以及地应力密切相关。从图中可以看出,巷道塑性区半径随着围岩的黏聚力和内摩擦角的增加而减小。并且随着地应力的增加,减小幅度越明显。这说明通过增加巷道围岩的物理力学性能可以有效控制巷道塑性区的扩展以及巷道位移。并且在深部地应力较高的地方,增加围岩物理力学性能对控制巷道稳定性效果越显著。

图2 巷道塑性区半径、巷道位移与围岩

根据图3可知,巷道塑性区半径随着支护强度的增加而减小,且巷道原岩应力越大,效果越显著。通过以上分析可知,对于深部巷道的塑性区控制,可以通过提高支护体支护强度和增强围岩的物理力学性能实现。

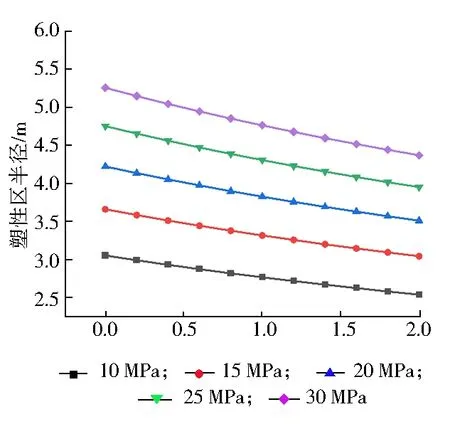
图3 塑性区半径与支护体支护强度之间的关系

2 深部巷道控制数值模拟

根据某矿巷道的地质资料,建立巷道的数值模拟模型(图4)。该模型长50 m,高36 m,宽3.2 m,共有17 100个节点、13 310个单元。模拟埋深900 m,竖直和水平方向分别施加30 MPa的均布荷载。X和Y方向的边界限制水平位移,底面Z方向限制竖向位移。岩石物理学参数见表1.

表1 岩石物理力学参数

图4 深部巷道有限元模型

2.1 地应力大小对巷道塑性区半径的影响

深部巷道的埋深大,地应力水平较高。通过施加不同的初始应力模拟不同的埋深。本文利用有限元软件模拟了无支护条件下,原岩应力大小对巷道塑性区半径的影响。通过图5的(a)、(b)分别表示地应力为30 MPa和15 MPa时,巷道开挖后的塑性区分布情况。地应力水平越高,巷道塑性区半径越大。当地应力大小从30 MPa减小到15 MPa时,巷道顶部的塑性区半径减小了65.8%,帮部塑性区半径减小了48.9%,底板的塑性区半径减小了45%.可以发现地应力大小对巷道围岩塑性区半径的影响较为显著。这也是深部巷道难以控制的根本原因。

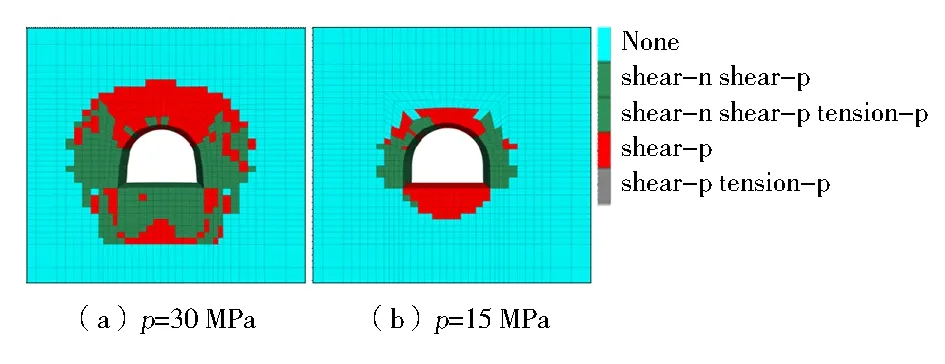
图5 不同地应力水平下的塑性区半径

2.2 支护强度大小对巷道塑性区半径的影响

利用数值计算模型模拟了不同支护强度对巷道塑性区的分布的影响。水平应力和竖直应力分别设置为30 MPa.支护构件设计为直墙半圆拱形的U钢支架,采用Beam单元进行模拟。将支护强度转化为弹性模量、惯性矩等参数,输入模型进行对比计算。图6显示了支护强度分别为0.5 MPa和1 MPa时,巷道开挖后塑性区的分布情况。可以看出,随着支护体支护强度的提高,巷道的塑性区半径明显减小,增加了支护强度的巷道顶部塑性区半径减小了50%.由于支架形状为直墙半圆拱,未形成封闭的结构,因此巷道底板的塑性区面积较大。

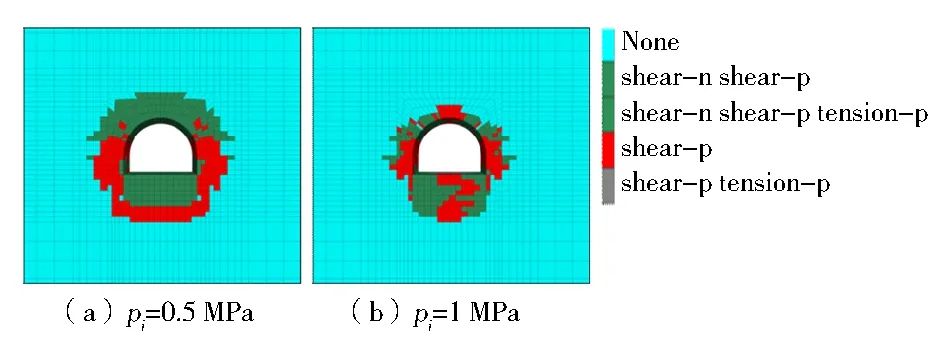
图6 不同支护体支护强度下塑性区半径

2.3 围岩的力学性能对巷道塑性区半径的影响

由于巷道在开挖之后,巷道周围的围岩强度处于峰值后的残余强度阶段,在空气和水的作用下,围岩的力学性能下降明显,塑性区的范围也逐渐扩大,极易造成支护体的失效,进而导致巷道失稳破坏。因此研究巷道围岩的力学性能对深部巷道的稳定性控制至关重要。

在有限元计算中,将距离巷道壁6 m范围内的围岩分成一个组,在开挖之后,对这个范围内的围岩重新赋予围岩力学参数。水平和竖直方向分别施加30 MPa的初始应力。图7(a)为开挖之后不改变围岩力学参数的情况,图7(b)为将巷道周围6 m范围内的围岩的黏聚力和内摩擦角分别扩大一倍的情况。从图7中可以看出,增加了巷道周围围岩的力学性能之后,拱顶处的塑性区半径减小了50.4%,帮部的最大塑性区半径减小了54.0%.底板处的塑性区半径减小了20.1%.可见,增加巷道周围围岩的力学性能对抑制巷道塑性区的扩展有显著效果。

图7 不同围岩力学参数下塑性区半径

3 结 语

1) 给出了深部巷道塑性区半径的计算公式,发现影响塑性区半径的因素主要有地应力大小、围岩力学参数和支护体的支护强度。将巷道数据代入公式计算可知,巷道塑性区半径随着地应力的增加而增大,随着围岩黏聚力和内摩擦角的增加而减小,随着支护体支护强度的增加而减小。

2) 通过数值模拟验证了地应力、支护体支护强度、围岩力学性能对巷道塑性区的影响。以拱顶处的塑性区半径为指标,地应力从30 MPa减小到15 MPa,塑性区半径减小了65.8%.支护体支护强度从0.5 MPa增加到1 MPa,塑性区半径减小了50%.将巷道周围围岩的力学性能增强后,塑性区半径减小了50.4%.