基于模态柔度的高桩码头损伤识别方法研究∗

张汝学，郑永来，韩雨莘，肖 飞，2

（1.同济大学土木工程学院，上海 200092； 2.中建港航局集团有限公司，上海 200940）

0 引言

高桩码头是我国港口码头主要的结构形式之一，承载能力强、消浪效果好，被广泛应用于软土地基区域。 在长期的服役过程中，高桩码头受到船舶靠泊荷载、波浪荷载、氯离子侵蚀作用而出现混凝土保护层脱落、裂缝开展和钢筋锈蚀等现象。 这些现象极大影响了码头的安全性。 随着结构健康概念的兴起，了解高桩码头构件的健康状态和损伤程度对确保码头安全生产具有十分重要的意义。

损伤识别是结构健康中的关键内容，分为静力学检测和动力学监测。 基于静力检测的方法是通过测量结构在受到静力荷载作用下产生的静力响应参数（挠度、应变、位移等），将这些参数的测量值与理论计算值进行残差分析以实现结构的损伤识别［1］。 Buda 等［2］等提出了静力荷载作用下Euler-Bernoulli 梁的损伤识别方法，利用有限元模型响应和实验数据两者之间的误差函数进行损伤识别。Eng 等［3］等提出了2 种计算方法以重建Euler-Bernoulli 梁的刚度分布并基于此实现损伤检测，之后通过静力试验测试了4 根具有预设损伤的梁验证了2 种方法的有效性。 Seyedpoor 等［4］利用损伤引起的静态应变能变化作为损伤识别指标，提出了一种结构多损伤定位方法，并通过3 个算例说明了该方法在噪声干扰的情况下能够准确定位结构损伤。陈孝珍等［5］首次将灰色相关性分析的概念引入损伤识别领域，提出了根据静态位移曲率置信因子识别并定位损伤的方法。 寇晓娜［6］首次将挠度影响线（包括一、二阶导数）应用于桥梁结构损伤识别，并通过多种损伤工况的数值模拟和室内模型试验进行验证，该方法在准确定位简支梁损伤位置的同时还可以确定损伤程度。

基于静力损伤检测方法具有操作简单和检测精度高的特点。 但是，该方法大多适用于陆地结构。 而高桩码头处于水陆交界区域，此方法具有局限性。

基于结构动力学理论，结构损伤会引起结构动力特性的变化，一般表现为刚度降低或有效截面减少，进而引起结构动力体系的刚度、阻尼和质量分布的变化［7］。 基于动力特性的损伤识别方法均建立在该理论基础之上，通过损伤发生前后的结构模态特征（频率、振型和阻尼）的差异作为损伤评估的指标。

结构损伤表现为局部构件的刚度降低，而柔度矩阵作为刚度矩阵的逆矩阵，可以用于损伤识别。Pandey 等［8］首次建立了一种基于模态柔度矩阵的损伤识别方法，通过悬臂梁模型验证了这一方法的合理性及有效性，并且通过在钢梁上收集的实测数据加以佐证。 试验结果表明了模态柔度矩阵可从几个低阶的模态振型中简便、准确地计算得到，且易于测量。 Jing 等［9］提出了广义模态柔度矩阵的概念，并推导了灵敏度计算公式，进一步降低了忽略高阶模态的影响。 Katebi 等［10］通过平面桁架和框架有限元模型检验了基于广义模态柔度矩阵在损伤识别中的准确性和鲁棒性。 王启明等［11］通过有限元模拟和物理模型试验研究模态柔度差在高桩码头损伤识别中的适用性，获得了较好的结果。 戴斌［12］提取结构损伤前后柔度矩的对角元素，运用差分法得到柔度变化率曲率指标，成功识别了简支梁单处与多处的损伤。

上述研究成果表明，模态柔度差与柔度变化率曲率可应用于结构损伤识别。 然而以往研究多集中于简支梁和连续梁结构，具有明确的边界条件，然而高桩码头是典型的超静定结构。 同时，模态柔度差对损伤程度较为敏感，非损伤单元仍具有较大的柔度差值，易产生误判。 基于模态柔度差变化率的损伤指标，虽然其效果优于模态柔度差，但使用一阶模态数据的损伤识别准确度仍有所欠缺。

因此，本研究在以往学者研究成果的基础上，通过数值模拟建立高桩码头结构段有限元模型，通过设置单个单元损伤与2 个单元损伤共六类工况，研究模态柔度差与模态柔度差曲率在高桩码头损伤识别的效果。 此外，不同于只采用一阶模态数据，本文将二阶模态数据引入损伤指标中，研究其提升损伤识别准确度的有效性。

1 基于模态参数的损伤识别方法

1.1 模态柔度法

多自由度无阻尼体系的自由振动方程为：

式中：［M]为结构的质量矩阵；［K]为结构的刚度矩阵；{} 为结构的加速度响应向量； ｛y｝ 为结构的位移响应向量，｛0｝ 为元素为0 的列向量。 将该微分方程的通解代入式（1），得到特征方程：

令｜［K］－ω2［M］｜＝0 可得n个正根，每个ωi对应一个幅值向量｛φ｝i，可得模态矩阵：

结构的模态质量矩阵、模态刚度矩阵和谱矩阵分别为：

将式（4）～（6）代入式（2），并将振型矩阵进行质量归一化，得到：

对式（7）等号两边同时求逆矩阵，然后左乘Φ，右乘ΦT可得：

根据结构力学中的定义，柔度矩阵是刚度矩阵的逆矩阵。 因此，式8 可以表示为结构的柔度矩阵，并用［F]表示。

1.2 损伤指标

通过对柔度矩阵进行不同的计算处理，可以构建多个损伤指标，本文选择其中经过较多检验的4个损伤指标柔度差δF、柔度变化率RFD（rate of flexibility diagonal，RFD）、均匀荷载面曲率差ULSC（change in uniform load surface curvature）和柔度曲率差δFc（flexibility curvature）进行研究。

2 有限元模拟

2.1 模型简化

选取上海港军工路港区某顺岸式高桩码头为原型结构，码头结构全长128m，宽26.7m，由前方的作业结构主体和后方的接岸结构组成。 每个结构段由7 榀横向排架构成，排架间距7m。 每榀排架内有5 根全直桩和1 根斜桩，基桩均为边长600mm 的方桩。 上部结构由上横梁、下横梁和面板组成。 上横梁高1.6m，宽0.4m；下横梁高0.8m，宽0.9m；纵梁高1.6m，宽0.4m；板厚0.8m。

2.2 建立有限元模型

本研究着重关注基桩在损伤前后的模态振型变化，因此在建模时不考虑基桩和土体之间的桩土相互作用，改为在所有基桩底部施加固定约束。 考虑等效抗弯刚度折减问题，基桩的计算长度采用JTS 167—4—2012《港口工程桩基规范》中的“m”法计算，并依据计算结果对码头横向排架断面进行简化建模（见图1）。 计算后的基桩长度如表1 所示。以单榀排架为基础，采用ABAQUS 有限元软件建立高桩码头结构段有限元模型，如图2 所示。

表1 基于“m”法等效后的各基桩计算长度Table 1 The equivalent length of each foundation pile calculated based on the “m” methodmm

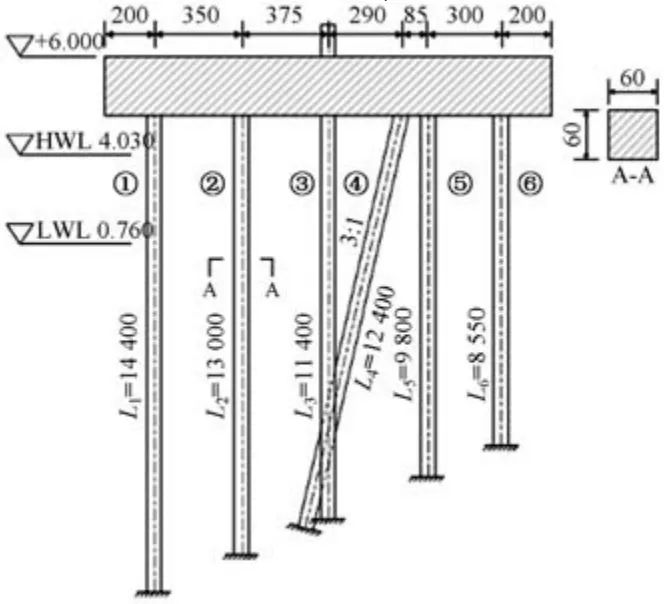
图1 基于“m”法的高桩码头结构断面计算简图Fig.1 Simplified dock structure section based on the ＂m＂ method

图2 有限元模型Fig.2 Finite element model

模型中所有构件均选取ABAQUS 中的C3D8R单元进行模拟。 分别创建码头面板、纵梁、横梁和基桩构件，通过装配各构件组成高桩码头整体结构段，各构件间的接触面完全耦合。 模型中的材料参数如表2 所示。

表2 材料参数Table 2 Material parameters

基于嵌固点法理论，高桩码头模型的基桩底部施加固定约束，限制全部位移，码头上部不施加任何约束。

2.3 有限元模型合理性分析

为验证数值模型的合理性，分别对有限元模型的频率和模态振型进行初始分析。 通过数值计算得到高桩码头结构段有限元模型的前10 阶固有频率值，如图3 所示。

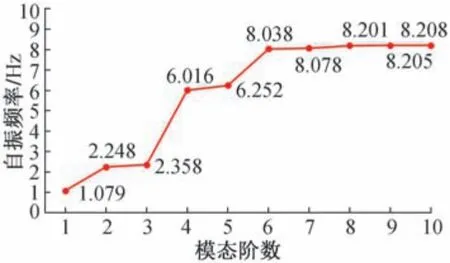
图3 各阶模态下的结构自振频率分布Fig.3 The self-resonant frequency distribution of the structure in each order of modes

由图3 可知，有限元模型各阶自振频率的分布呈现较为明显的两阶段特征。 前三阶模态的自振频率逐阶增大但相差不大，三、四阶模态间自振频率出现明显跃升，更高阶模态间的自振频率存在微小的增长。

在现阶段的工程实践中，关于高桩码头结构原型的实地振动测试结果较少，只有少数研究人员进行的相关工作受到广泛认可。 Boroschek 等［13］对智利的Ventanas 港某高桩码头结构段进行了实地振动测试，得到了码头结构段的前三阶频率。 程丽娜等［14］运用环境激励技术测量了中国外海海岛某高桩码头在3 个不同潮位时段的振动情况，得到了该码头结构的前三阶频率。 将本研究中的有限元模型频率计算结果与上述2 项研究中的结构段频率进行对比分析，如表3 所示。

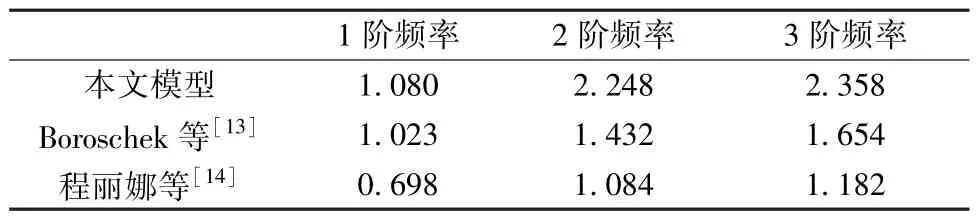
表3 高桩码头结构段实测频率Table 3 Measured frequency of high-pile wharf structural sectionHz

经过对比可知，本文建立的有限元模型的前三阶自振频率与2 项研究中的实测数据处于同一数值水平，整体略高。 前三阶频率间的增长趋势与实测数据表现出相同的特征，说明本文建立的有限元模型能够较为准确的反映实际工程中高桩码头结构段的动力特性。

2.4 工况设置

相比于其他土木工程结构，高桩码头在长期服役过程中受到多重荷载作用，其中，基桩受荷载作用最为明显。 受船舶靠泊产生的水平撞击作用，码头的斜桩和前沿的直桩的顶部易产生破坏。 同时，码头前沿的直桩直接接触水域，受水域环境影响最为明显。 因此，在海洋腐蚀和波浪冲刷作用下，码头前沿的直桩更易产生破坏。 大量针对高桩码头的健康检测表明，实际的码头结构中，斜桩与码头前沿直桩的顶部位置出现混凝土剥落、水平裂缝开展、钢筋锈蚀裸露等损伤。 综上所述，本研究选择结构段中部排架前沿的直桩为模拟损伤对象。

基桩出现的损伤类型包括混凝土的受拉破坏、混凝土受压开裂、钢筋锈蚀引起的混凝土锈胀，这些损伤本质是桩的局部刚度降低。 在有限元模型中，保证模型几何尺寸一致的前提下，通过降低材料的弹性模量实现刚度降低。

选取沿x正向的第5 根近海侧前直桩作为损伤基桩，将基桩等分为24 段共25 个节点，每段长0.6m，从24 个单元上到下依次标为1 ～24 号单元，25 个节点从上到下依次标为节点1 ～25，将1 号，6号，12 号和15 号单元作为损伤单元，分别代表桩顶位置、潮差区桩身、桩身中部和桩身其他位置的局部损伤。 基桩分段和损伤单元设置如图4 所示。

图4 损伤基桩分段和损伤单元Fig.4 Damage to pile segments and damage units

同时设置单个单元损伤和两单元损伤工况。 单损伤工况设置如表4 所示，两单元损伤如表5 所示。

表4 单个单元损伤工况设置Table 4 Single unit damage condition

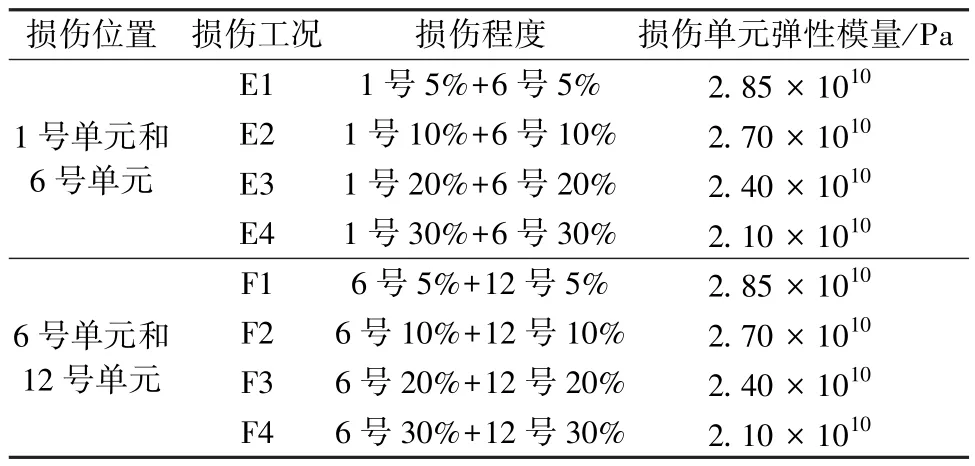
表5 两单元损伤工况设置Table 5 Double unit damage condition

3 结果与讨论

3.1 基于模态柔度差指标的损伤识别结果

提取设计工况下，选择一阶和二阶模态数据计算各单元的模态柔度差，如图5 ～10 所示，可得出如下结论。

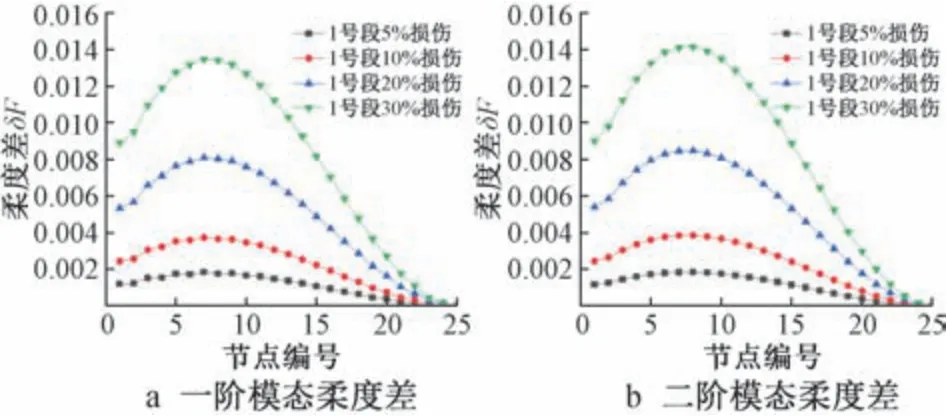
图5 A1～A4 损伤工况下的模态柔度差Fig.5 Modal flexibility difference of A1～A4 damage conditions

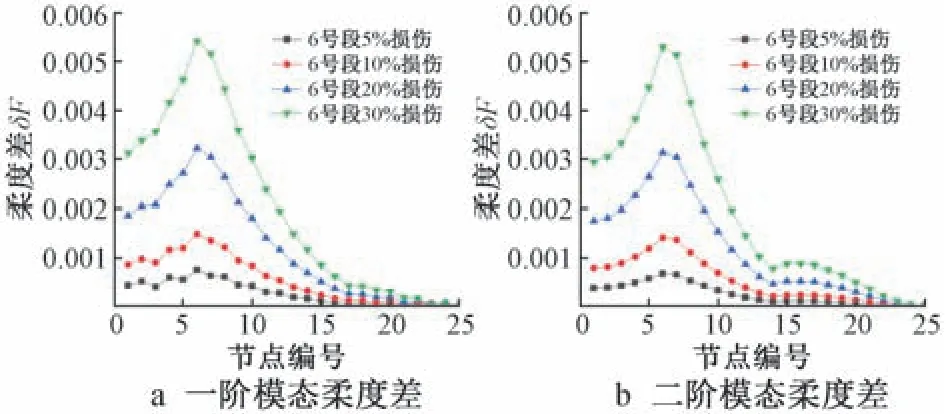
图6 B1～B4 损伤工况下的模态柔度差Fig.6 Modal flexibility difference of B1～B4 damage conditions

图7 C1～C4 损伤工况下的模态柔度差Fig.7 Modal flexibility difference of C1～C4 damage conditions

图8 D1～D4 损伤工况下的模态柔度差Fig.8 Modal flexibility difference of D1～D4 damage conditions

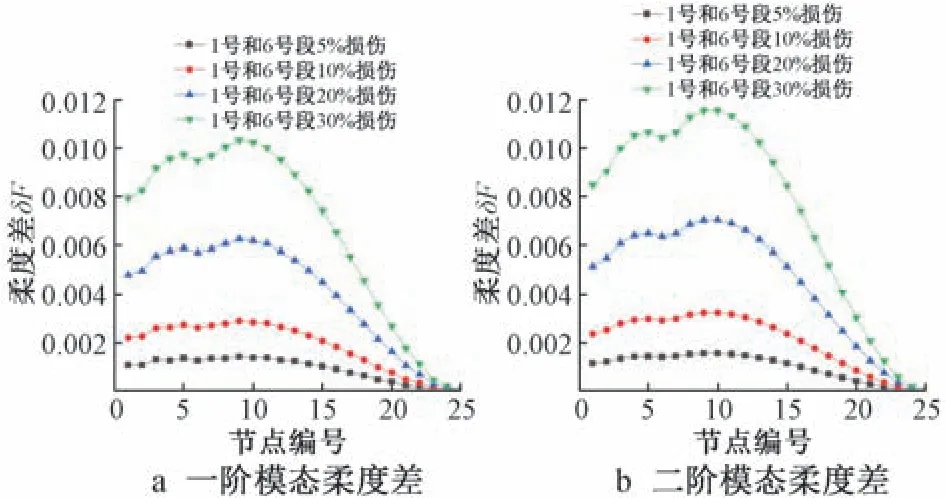
图9 E1～E4 损伤工况下的模态柔度差Fig.9 Modal flexibility difference of E1～E4 damage conditions

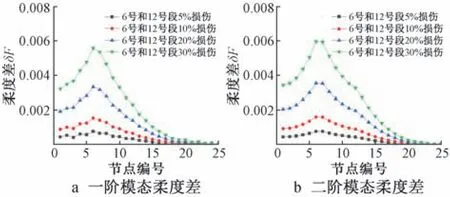
图10 F1～F4 损伤工况下的模态柔度差Fig.10 Modal flexibility difference of F1～F4 damage conditions

1）当损伤发生在桩身自由段时，曲线上柔度差最大值显示出损伤位置；当损伤发生在桩顶时，柔度差最大值并没有出现在1 号段对应的部分，而是在6 号单元对应的位置。 由此可知，同一损伤工况下，柔度差的最大值可以准确识别出桩身自由段的损伤位置（6 号，12 号和15 号），但该指标在桩顶位置号的识别中失效。

2）柔度差指标在桩顶附近位置的值较大，在桩底附近位置的值较小。 说明该指标一定程度上放大了桩顶附近在损伤前后的振动变化，导致在某些损伤工况下桩顶附近单元的柔度差值较大且接近损伤位置处的柔度差峰值，对于损伤位置识别是一种较为严重的干扰。

综上所述，模态柔度差指标对于桩顶单元的损伤无法准确识别，只能识别出桩身自由段的损伤，且在对桩身自由段的识别中存在较大干扰。 因此可以认为该指标并不适用于基桩的局部损伤识别。

3.2 基于模态柔度差曲率的损伤识别结果

基于数值模拟结果计算模态柔度差曲率，结果如图11～16 所示。

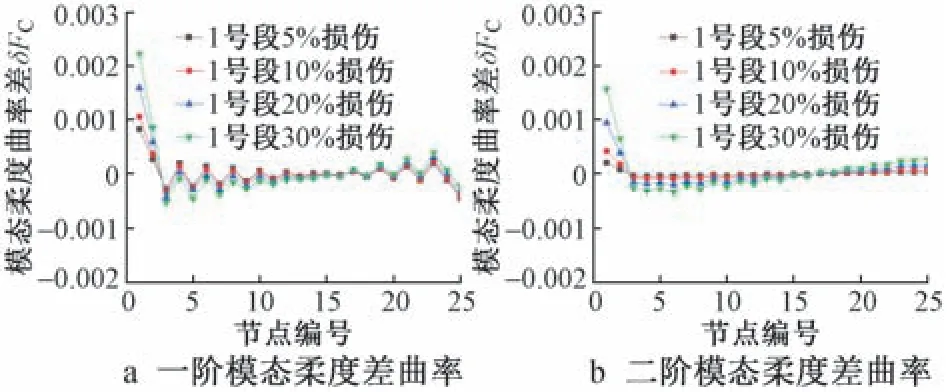
图11 A1～A4 损伤工况下的模态柔度差曲率Fig.11 Modal flexibility differential curvature of A1～A4 damage conditions

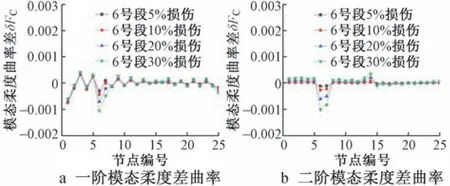
图12 B1～B4 损伤工况下的模态柔度差曲率Fig.12 Modal flexibility differential curvature of B1～B4 damage conditions

图13 C1～C4 损伤工况下的模态柔度差曲率Fig.13 Modal flexibility differential curvature of C1～C4 damage conditions

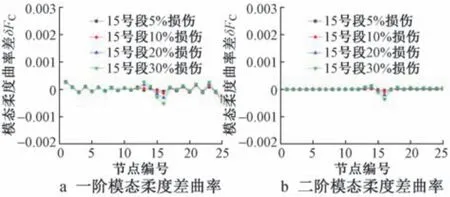
图14 D1～D4 损伤工况下的模态柔度差曲率Fig.14 Modal flexibility differential curvature of D1～D4 damage conditions

图15 E1～E4 损伤工况下的模态柔度差曲率Fig.15 Modal flexibility differential curvature of E1～E4 damage conditions

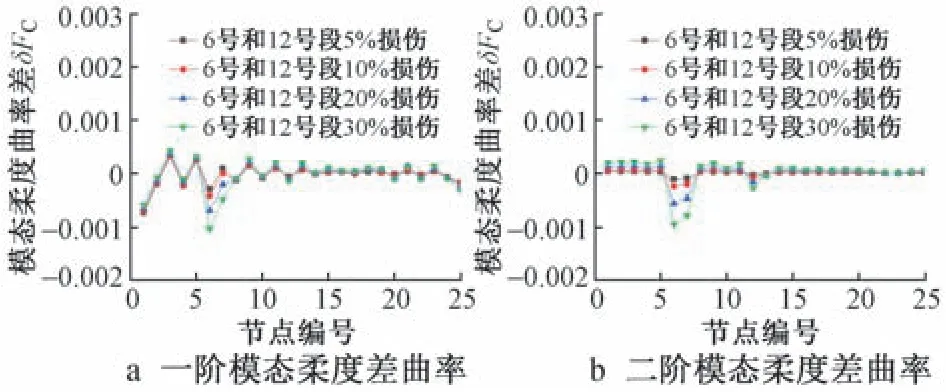
图16 F1～F4 损伤工况下的模态柔度差曲率Fig.16 Modal flexibility differential curvature of F1～F4 damage conditions

1）在单损伤工况下，δFC曲线上的突变值对应的单元为工况中设置的损伤单元。 这表明模态柔度差曲率能较为准确的识别出损伤单元，并且该方法对基桩全段位置的单独损伤具有较好的识别效果。

2）在多损伤工况下，δFC指标在一阶模态下的识别效果略有减弱，但在二阶模态下仍有较好的识别效果。 在E1～E4 损伤工况下，δFC曲线对于1 号段的损伤能够准确定位，但在节点1 ～10 的曲线部分存在干扰信息，导致无法定位6 号段的损伤。 在F1～F4 损伤工况下，δFC曲线对于6 号段的损伤能够准确定位，但在12 号段对应的曲线部分没有明显突变，导致漏判损伤单元。

3）δFC指标在二阶模态下的识别效果整体优于一阶模态。 相较于一阶模态，二阶模态下的δFC曲线更加平滑，曲线上突变的位置更易于观察。

综上所述，一阶与二阶振型下的模态柔度差曲率都能较好的识别出损伤位置，但指标在少数复杂的多损伤工况的一阶模态下会有误判或漏判现象。同时采用一阶和二阶模态柔度差曲率能够有效提高损伤位置识别准确度。

3.3 损伤指标对比

损伤指标对基桩不同位置的识别效果如表6～7所示。

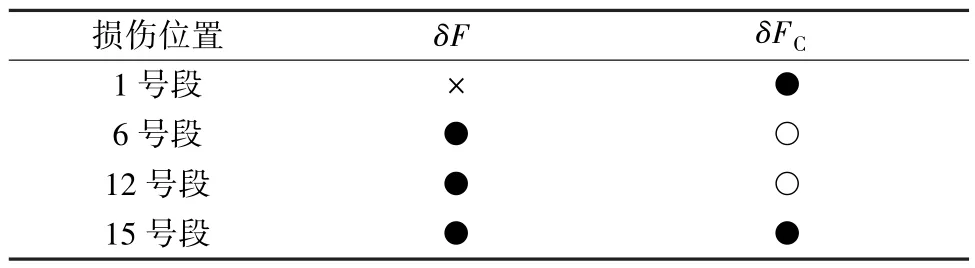
表6 单损伤工况下各损伤指标的识别效果Table 6 Identification effect of each damage index under single damage condition

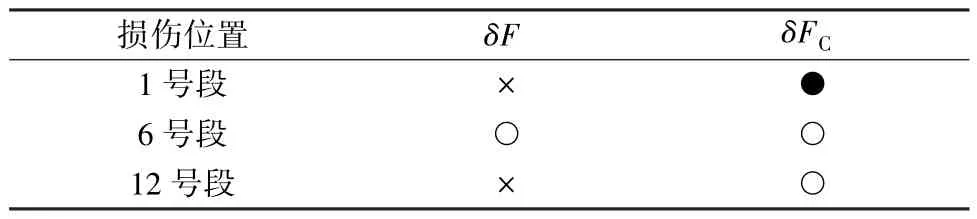
表7 多损伤工况下各损伤指标的识别效果Table 7 Identification effect of each damage index under multiple damage conditions

由上述对比可知，基于模态柔度差指标的损伤识别效果较差，该方法在某些特殊位置或二阶模态下能够获得有效的识别效果；模态柔度差曲率在全段较为平滑，只在损伤位置处出现明显突变，呈现出尖峰的形状，该方法能准确的识别损伤位置。 同时，高损伤度下，模态柔度差曲线的弯曲程度明显高于低损伤度，且在未损伤位置也具有较大的模态柔度差；而模态柔度差曲率在非损伤位置的值基本为0，使得该方法能够有效排除干扰信号。

上述2 个指标出现差异是由于模态柔度差是基于单个单元在损伤前后的柔度数据，而模态柔度差曲率则是同时基于损伤单元和非损伤单元的柔度数据。 因此，同时使用多个单元的模态柔度数据能够有效提高损伤识别准确度。

4 结语

1）基于模态柔度差和模态柔度差曲率的损伤指标都能识别出基桩损伤位置。 模态柔度差更适用于非桩端位置的单个损伤，而模态柔度差曲率能够较好识别出基桩全段单个或多个损伤。

2）由于只采用了单个单元的模态柔度，高损伤度下的模态柔度差的值明显大于低损伤程度，损伤位置信号不够明显；采用多个单元模态柔度数据获得的模态柔度差曲率的值只对损伤敏感，对损伤程度不敏感，其曲线具有明显的损伤识别信号。

3）基于一阶模态柔度数据的损伤指标都能够识别出损伤位置，但在特殊状态下仍有可能出现误判。 此时，采用二阶模态柔度数据能够有效剔除误判。 因此，同时采用一阶与二阶模态柔度数据进行损伤识别，可以提高损伤识别准确度。