地震不连续信息的自适应方向增强检测及应用

黎康毅，陈学华*，，吴昊杰，吕丙南，赵晨斐

（1.成都理工大学油气藏地质及开发工程国家重点实验室，四川成都 610059；2.成都理工大学地球探测与信息技术教育部重点实验室，四川成都 610059）

0 引言

断层和裂缝的连通网络影响地下地层的形态及地震资料处理、解释结果，要获得精确的地质模型，特别是在逆掩断层及相关褶皱带，需要精确检测、解释断层与裂缝。

存在复杂断层地区的三维地震数据质量受采集、处理等环节的多种因素影响。在地下地质结构较复杂地区的地震资料往往信噪比较低，需要压制随机噪声、提高地震数据的质量，以有效实现可视化和属性提取。通过应用不同的滤波器、数据转换和属性组合技术，可以增强断层与裂缝的地震响应特征。Marr[1]、Witkin[2]、Koenderink[3]阐述了多尺度图像分析的重要性，并在数字图像处理中引入尺度空间理论；伍鹏等[4]将二维高斯迭代平滑滤波用于曲率属性分析，但是没有考虑裂缝方向，不能突显不同方向的异常信息；在前人研究[5-7]的基础上，Cho 等[8]、Park 等[9]应用自适应Gabor 滤波强化手指静脉图像并取得了不错的效果；Chen 等[10-12]提出了一种多尺度曲率计算方法及地震定向滤波新算法，为结合裂缝方向选取最佳滤波器提供了理论基础；周元茂等[13-14]结合地震体曲率与各向异性高斯滤波方法，形成了组合型方向体曲率分析方法，可以突显不同方向的异常信息，但是缺少自适应性，需要人为提取裂缝方向；徐赫等[15]将旋转窗加入希尔伯特变换，以提取地震资料中不同方向的有效信息；Jabar等[16]引入一种综合属性和图像的分析技术增强地震断层图像。

本文结合前人方法，提出地震不连续信息的自适应方向增强方法，根据裂缝方向选取高斯滤波器方向对地震数据二次迭代滤波，可有效压制干扰、突出地震数据的有效信息，从而增强特定方向的不连续信息并提取高精度地质异常信息。

1 方法原理

本文提出的地震不连续信息的自适应方向增强方法，根据裂缝走向不断地更换各向异性高斯滤波器的方向，使数据所受的异常干扰小，同时保留更多有效信息。具体操作分为五个步骤（图1）。

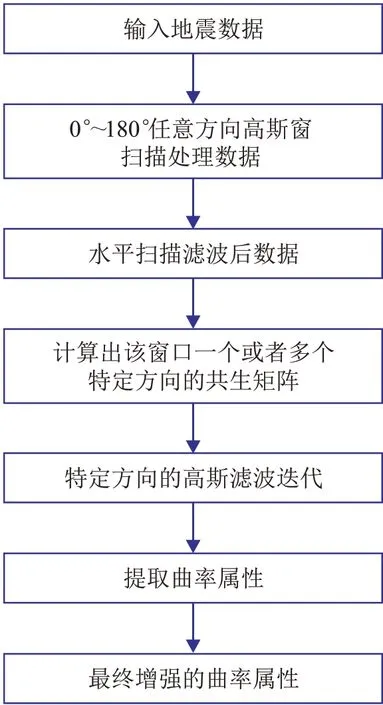
图1 不连续信息增强流程

（1）在0°～180°范围的所有给定方向的高斯窗扫描输入地震数据，在每个位置分别选取窗内振幅之和的最大值方向的处理结果；

（2）选定时窗扫描处理数据，将处理数据映射为L级灰度构成地震纹理基元体；

（3）求取时窗内数据特定方向的共生矩阵纹理参数，并判断处理数据的特定方向；

（4）将判断的裂缝方向代入各向异性高斯滤波方向矩阵进行二次迭代；

（5）对处理数据采用各向异性体曲率属性分析方法得到增强的最终图像。

1.1 灰度共生矩阵

1973年，Haralick 等[17]提出了灰度共生矩阵模型(GLCM)，随后被用于揭示图像的纹理特征[18-22]。

其方法流程为，首先确定时窗宽度，扫描地震数据并进行灰度处理而构建灰度共生矩阵，设最大灰度级为L，假设水平方向(Crossline 方向)的测线数目为xmax，则地震数据的水平空间域为Nx={1,2,…,xmax}；假设垂直方向(Inline 方向)的采样点数为ymax，则地震数据的垂直空间域为Ny={1,2,…,ymax}。设数据点对的距离为l，数据点对间的方向角为θ，则在(m,n)处灰度级g(m,n)=i的像素点与相距为l、方向为θ的(p,q)处灰度级g(p,q)=j的像素点，在图像中出现的概率为P(i,j,l,θ)(图2)，生成的灰度共生矩阵为

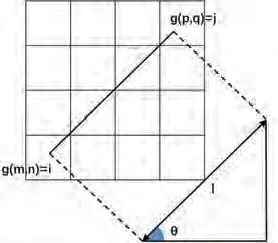
图2 数据点对之间的关系

式中L为最大灰度级。由于l、θ的选择不同，会导致不同的统计结果，如当θ为0°、90°时，共生矩阵元素为

选取最常用的能量E、相关性C、熵H及对比度I等4个纹理参数判断裂缝及突出蜿蜒通道的方向，即

其中

通过时窗扫描地震数据，每扫描一次便计算一次灰度共生矩阵，并得到共生矩阵的4个纹理参数，通过

判断时窗位置的方向。如果满足式(6)或式(7)，则输出时窗的数据方向；如果式(6)和式(7)所得时窗方向不同或E、C、H、I全为0，则说明时窗数据没有明显的特征方向，跳过并继续扫描数据。

图3 为一个正十六边形模型，其中每一边的内角均为22.5°。使用20 个采样点的时窗扫描图3，分别计算θ为0°、22.5°、45°、67.5°、90°、112.5°、135°、157.5°的共生矩阵，通过共生矩阵得到各方向的纹理参数。将不同方向的4 个纹理参数代入式(6)、式(7)，选取式(6)、式(7)对应的角度作为该处纹理的方向。

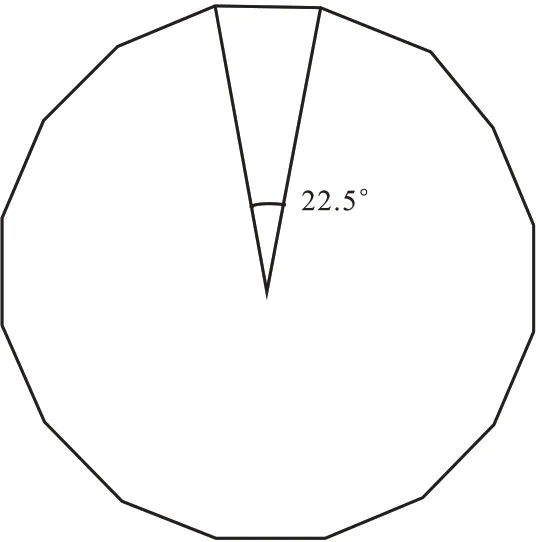
图3 正十六边形模型

图4 为判断纹理方向的模拟测试结果。由图可见，准确判断了正十六边形的各个方向，表明了方法的可行性。

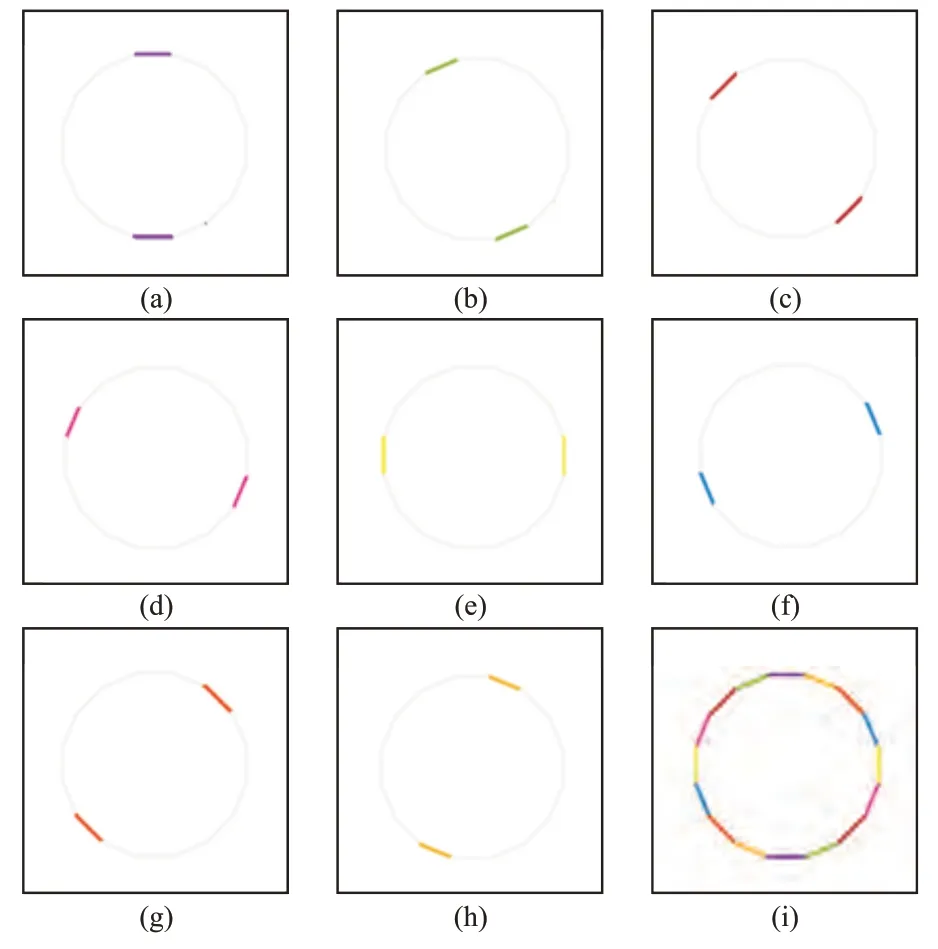
图4 判断纹理方向的模拟测试结果

1.2 各向异性高斯滤波器

传统高斯函数滤波的基本原理是将高斯核函数与原始信号卷积，以二维高斯滤波为例，滤波器表达式为

式中：x和y表示二维高斯函数的两个方向，当x方向和y方向呈各向同性时，高斯滤波即为各向同性滤波(图5a)；σ为高斯函数的方差。

图5 二维高斯滤波器

将传统高斯滤波器中的x和y与方向矩阵相乘，并在在x、y方向选取不同的尺度，就得到旋转变换后的各向异性高斯滤波器，其滤波器表达式为

式中σx和σy为高斯函数的方差，分别决定高斯核宽度和长度，与平滑程度有直接关系，σx越大，x方向高斯窗口越宽，σy越大，y方向高斯窗口越宽，平滑程度越好。当σx≠σy时，高斯滤波即为各向异性滤波(图5b)。

为了利用各向异性高斯滤波描述地震数据中的蜿蜒河道、裂缝和其他地质不连续点，需要考虑σx、σy和θ的变化（图6）。文中提出了一个基于各向异性高斯滤波方法的工作流程突出地震数据中的蜿蜒通道和其他地质不连续点。

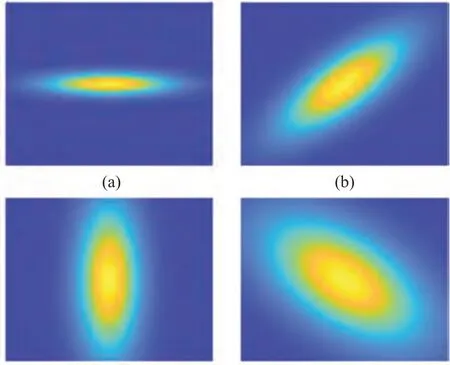
图6 各向异性高斯滤波器

根据实际地震资料中的裂缝尺度，给定各向异性高斯滤波器G(x,y,σx,σy,θ)的孔径和纵横比。然后用一系列不同方向的滤波器处理以分析点为中心的地震数据

式中：Gθ(x,y,σx,σy,θk)可以视为空间分析窗口；S(τ,xi,yj)是以(xi,yj)为位置点、以时窗位置τ为中心的地震数据；F(τ,xi,yj,θk)为滤波后地震数据，k为椭圆滤波器的方向。

对于0º～180º范围内所有给定的滤波方向θk，在每个空间位置取F(τ,xi,yj,θk)的最大值，即

其中F(τ,xi,yj)突出了真实方向的主要特征，而在其他方向抑制了噪声。

然后，定义地震方向滤波算子，得到时窗位置τ的地震数据

式中：w为时窗窗口长度的一半；M为时窗尺度。

1.3 三维各向异性体曲率分析

在三维地震数据中，一般需要将三维地震数据体先转化为倾角数据体，再根据倾角数据体计算任意点的曲率。可以根据复数道分析中的瞬时频率和瞬时波数计算三维地震数据体的视倾角

式中：ω为瞬时角频率；kx与ky分别为x与y方向的瞬时波数；px与qy分别为x与y方向的视倾角分量。

在此基础上，构造新的方位视倾角分量

式中β为根据地质构造方向而选取的角度。

根据最小二乘逼近原理，得到二次曲面方程

其中

式中f为常数。最大正曲率Kpos和最小负曲率Kneg是解释实际构造的主要地震属性，其表达式为

2 实际资料处理实例

为了验证本文方法在LH 地区的应用效果，分别利用一次方向各向异性高斯滤波和本文方法对三维叠后地震数据体进行0°、90°方向的滤波。图7 为LH地区地震振幅沿层切片。由图可见，在多个方向存在强噪声，从而难以识别有效的不连续地质信息，也难以辨识各种尺度裂缝的空间走向。

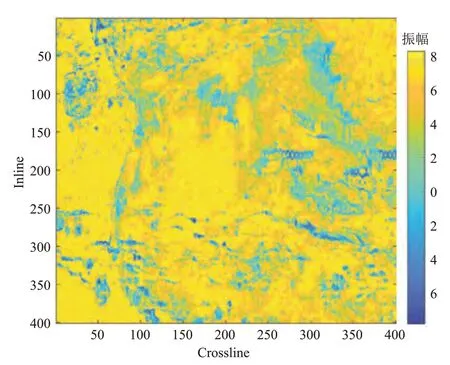
图7 LH 地区地震振幅沿层切片

图8 为一次方向的各向异性高斯滤波与本文方法得到的最大正曲率属性。由图可见：①90°一次方向的各向异性高斯滤波(图8a 的红色、绿色方框处)及本文方法(图8b 的红色、绿色方框处)明显增强了纵向不连续性信息及构造异常特征，且图8b 更明显；0°一次方向的各向异性高斯滤波(图8c 的红色、黄色方框处)及本文方法(图8d的红色、黄色方框处)则着重突出了横向构造特征，明显增强了断层及裂隙连续性，且图8d更明显。②与一次方向各向异性高斯滤波(图8a绿色箭头处、图8c 红色箭头处)相比，本文方法(图8b绿色箭头处、图8d 红色箭头处)明显突出了指定方向的地质异常构造。

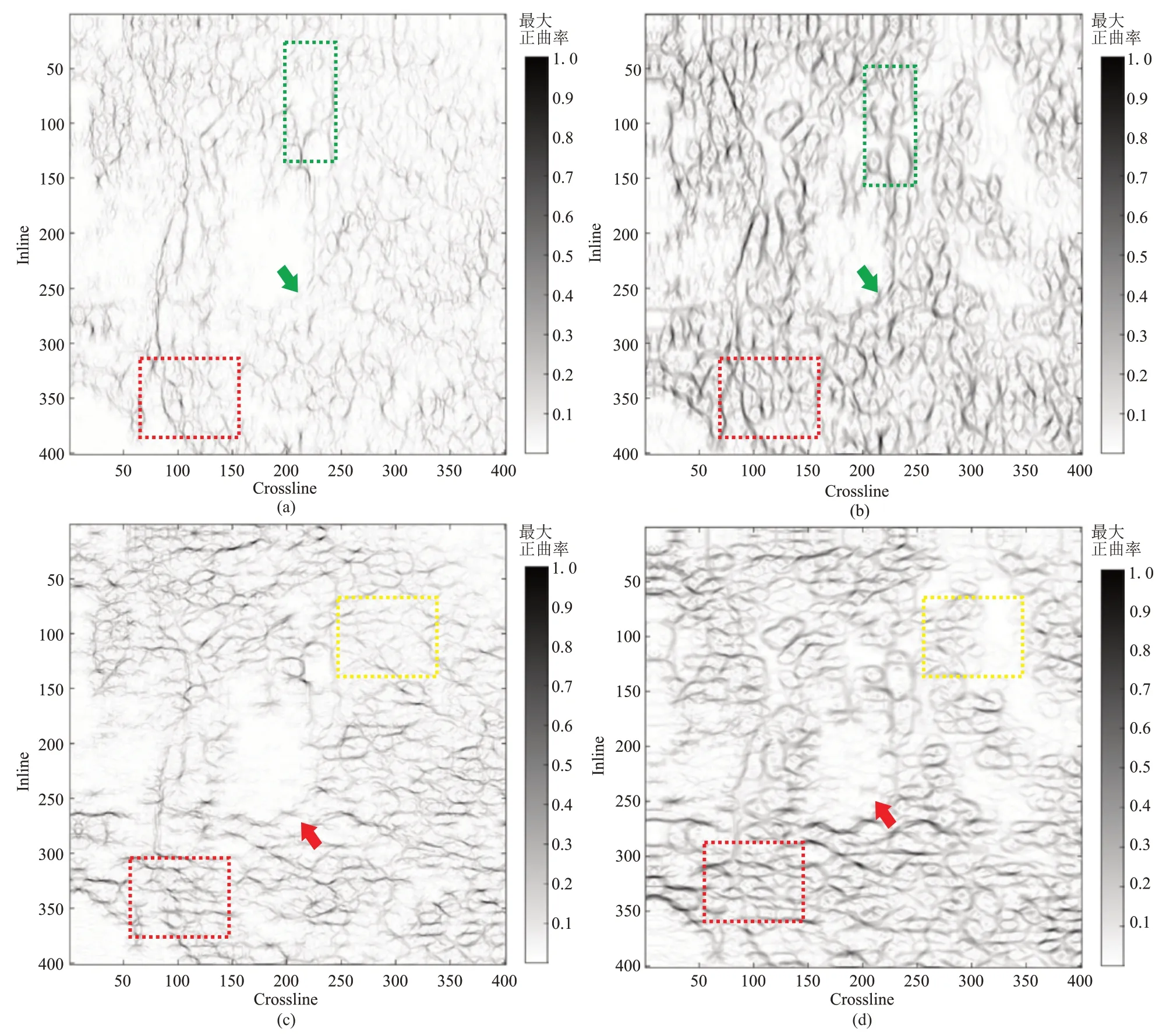
图8 一次方向的各向异性高斯滤波与本文方法得到的最大正曲率属性

为了突出裂缝及断层走向，使用灰度共生矩阵对一次方向的各向异性高斯滤波结果提取E、C、H、I等四个纹理参数（图9）。可见，LH 地区的断层及裂缝走向主要为90º、0º，小尺度裂缝及断层的走向多变。图10 为不同方法得到的实际地震数据的最大正曲率属性。由图可见：①原始最大正曲率属性的随机噪声干扰严重，构造、断裂展布不清晰（图10a）。②由一次方向的各向异性高斯滤波结果可大致看出断裂、褶皱、落水洞等的轮廓，但是细节不明显（图10b 的红色方框及绿色箭头处）。③本文方法处理结果（图10c）明显突出了断层及裂缝特征，并刻画了某些细小的地质异常构造，如一些细小的褶皱、落水洞、隐蔽裂缝等（图10c 的红色方框及绿色箭头处）。

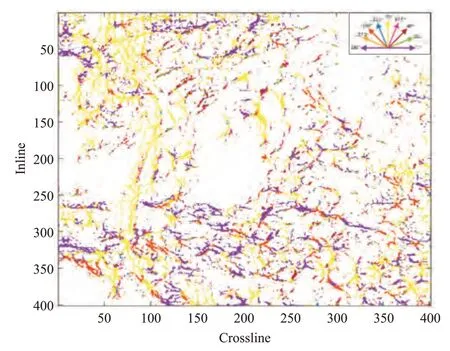
图9 地震数据的裂缝方向图

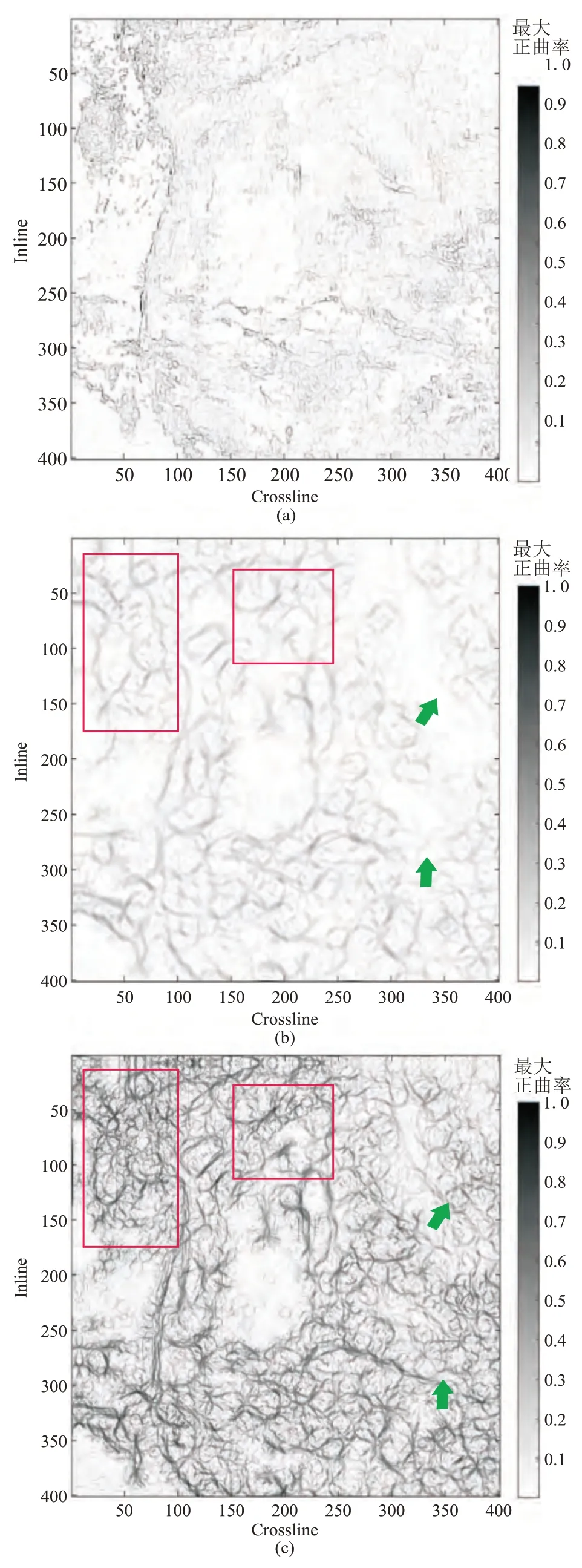
图10 不同方法得到的实际地震数据的最大正曲率属性

3 结束语

本文提出了一种地震不连续信息的自适应方向增强方法，在常规高斯滤波算法的基础上，推导了各向异性方向迭代高斯平滑滤波公式。该方法对地震数据进行两次时窗扫描，自适应地判断裂缝等异常信息的方向，再根据判断的方向选取匹配该方向的最优滤波器进行二次迭代处理，有效地压制与裂缝等方向不同的干扰信息，极大突出了地质构造特征，更好地反映了特定方向的构造细节和不连续性。同时该方法也可自行选取一个或多个特定方向，只展现所选方向的构造信息。该方法可为构造解释、了解断裂展布规律、储层预测等提供技术支持，体现了算法的可行性和优越性。