煤矿矿井水水质形成及演化的水动力场驱动作用及数学模型构建

孙亚军 ， 赵先鸣 ， 徐智敏 ， 张 莉 ， 陈 歌 ， 冯 琳 ， 李 鑫 ， 陈天赐 ， 袁慧卿 ，刘 琪 ， 郭 娟 ， 张 健 ， 刘嘉欣 ， 熊小锋

(1.中国矿业大学 资源与地球科学学院, 江苏 徐州 221116；2.矿山水害防治技术基础研究国家级专业中心实验室, 江苏 徐州 221116)

我国煤炭资源的开采方式以井工开采为主[1]，由于采掘活动对顶底板含水层的影响，通常会产生大量的矿井水[2-3]。同时，煤矿开采过程还必然引起区域地下水动力场的改变，这也是矿井水水质演化最主要的驱动力[4]。煤矿开采过程中，一方面，受顶底板采动破坏带的形成[5-6]、控水构造活化失稳[7]和封闭不良钻孔[8]、采空区积水[9]等影响，使矿区地下水动力场发生重大变化并进一步影响矿井水的水量及流速，这直接决定了参与水–岩、水–水混合作用等反应的水量及反应的时间，从而影响水质的形成与演化；另一方面，原始地层在人为扰动以后，其温度[10]、压力[11]、介质条件[12-14]、氧化还原[15]等理化条件也会发生明显的改变，由此引起矿井水中某些特征组分及微生物群落结构发生变化，打破了原有地下水中的物理–化学–生物反应平衡，进而进一步影响矿井水水质[16]。因此，矿井水水质的形成与演化是由煤矿区水动力场驱动，水化学场、微生物场[17]等多场协同作用的结果。目前，既能体现煤矿采空区特殊水动力场又能够表现多场作用的研究鲜有报道，并且煤矿采空区水动力场的特殊性及多场作用的复杂性也进一步限制了相关理论研究的推进。

笔者团队在国家重点研发项目的支持下，在大量分析我国煤矿水质演化的水动力场、水化学场、微生物场多场资料的基础上，提出了矿井水水质演化的垂向“三带”概念[4]：第1 带的水质演化受开采活动影响最小，主要与地下水自然流动与蒸发浓缩作用相关；第2 带多为煤矿常规生产阶段产生的矿井水，其水质形成与演化与不同含水层间的水–水混合作用以及水岩作用相关。根据《煤矿防治水细则》有关要求，生产矿井排水能力应满足能在20 h 内排出矿井24 h 的正常涌水量[18]，故正常生产矿井产生的矿井涌水一般会在24 h 内由井下排出，因此影响第2 带矿井水水质的水–水混合作用以及水–岩作用进行的时间相对较短，使得此水质带有较为明显的原含水层水质特征；在第3 带，此水质带是人类活动影响最为频繁的区域，在矿井开采时期，生产工作面和排水巷道中的地下水受矿井长期排水影响，水动力条件较好，但在已封闭的采空区中矿井水径流缓慢。来自各充水含水层的地下水在经历长时间的混合作用、水–岩(煤)作用、微生物作用等耦合后形成感观较差、微生物群落较为丰富的矿井污水[19]，即使在矿井闭坑以后，其水质形成和演化仍可在区域水动力场的影响下长期进行。因此，第3 水质带内的采空区积水是煤矿区矿井水污染研究的重点区域。目前针对煤矿区矿井水的水质形成及演化机理的研究主要是通过野外取样观测、室内批试验以及建立相应的数学、数值模型的方法研究矿井水的理化性质、特征组分迁移扩散行为以及水–岩作用及水–水作用强度，但对于采空区积水的水质形成过程中水动力场演化机理研究以及水动力场驱动下的多场作用机制研究相对匮乏。

在上述背景下，笔者以我国西北鄂尔多斯煤田某煤矿为地质原型，分别对煤矿采空区积水水质演化的水动力场作用以及水动力场驱动下的水化学场作用及微生物场作用进行综述(由于所选地质原型的采空区埋深超过500 m，温度变化主要受地温梯度影响，实测矿井涌水和主要充水含水层的水温25～28 ℃，变化幅度和差异较小，因此可忽略温度场的影响)；重点研究其水动力场的作用机制及数学模型，并开展模拟试验对数学模型进行验证；最后构建水动力场主导下多场耦合数学模型，以期为煤炭安全绿色开采与水生态环境保护提供理论支撑。

1 采空区积水形成的水动力特征

当工作面回采结束后，一般会在一定时间内撤出相关设备及材料，并进行永久性封闭，形成采空区。封闭后停止或减弱疏排水必然导致采空区内的地下水位缓慢回升，形成采空区积水。此时，井下采空区成为矿井涌水的汇集区域，同时也是地下水发生物理、化学及生物等多场作用(图1)的场所。因此，采空区积水的水质形成及演化是以水动力场主导，水化学场、微生物场等多场协同作用的复杂过程，具有高度的非均质性和时空变异性，然而相关针对性的研究较少，揭示采空区水质演化过程中水动力场驱动下的多场作用对于煤矿区地下水污染防控具有重要意义。

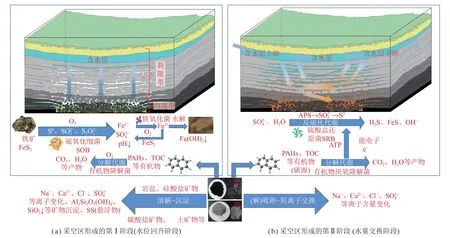
图1 封闭采空区积水水质形成与演化的多场作用Fig.1 Multi field coupling effect on the formation and evolution of goaf water quality

1.1 采空区积水的水动力条件演化

一般情况下，采空区封闭后，人为对煤层、地层的扰动停滞，在区域水动力场作用下，采空区逐渐被原生充水含水层水源充填，采空区积水会与采空区内的煤、岩等接触并产生一系列的水–水[20]、水–岩(煤)[21]以及微生物[22]等作用，且井下水动力条件随着采空区充水过程逐渐减弱，短期内采空区积水水质仍趋于劣化。采空区充满后，在水动力场作用下，采空区积水会随着区域地下水渗流方向运移，若遇到控水构造或其他导水裂隙还会与其他含水层产生水质混合，可能造成含水层间的串层污染。但在采空区封闭后的长期演化过程中，由于水动力条件减弱和采空区煤岩对某些水化学组分的吸附作用[23]，使得采空区积水水质得到改善。

对于研究区鄂尔多斯矿区某煤矿而言，主采煤层为侏罗系延安组3-1煤，其主要充水水源是顶板砂岩裂隙水(由于安定组砂岩含水层富水性较弱，主要充水水源为直罗组砂岩含水层)[24]。其对于研究区这种单一顶板充水含水层的封闭采空区，在不考虑人工抽排水、间接充水含水层以及大气降水的影响下，水动力场流动路线可以简化为2 个阶段，即采空区水位回升阶段和蓄满采空区–含水层水量交换阶段(后简称水位回升阶段和蓄满水量交换阶段)。如图1(a)所示，水位回升阶段适用于回采结束封闭采空区的初期，此阶段由于采动裂隙带及垮落带的存在，直接充水含水层中的地下水流入采空区，导致采空区内水位升高。当采空区内水位升高至直接充水含水层，采空区与直接充水含水层形成一个含水单元，此时采空区内的地下水流场与直接充水含水层的流场产生水量交换，如图1(b)所示，这一阶段直接充水含水层水从上游进入采空区后分为2 个部分，一部分沿着原含水层流向不变，另一部分则沿着导水裂隙带进入垮落带以及废弃工作面然后再经过导水裂隙带回到原含水层中，因此，这一阶段水量交换强度与流动路径上的渗透系数和直接充水含水层在采掘影响范围内的上下游水头相关。

1.2 水动力驱动下的水化学及微生物作用

1.2.1 水化学作用

在煤矿采掘过程中，采出空间顶板的岩层由于失去支撑而垮落，使得底板岩层的连续性遭到破坏，顶底板岩层裂隙成为导水通道，因此，采空区积水通常由采空区多层顶、底板含水层混合组成，其水质构成十分复杂[25]。而对于顶板单一充水含水层的煤矿区而言，在采空区封闭初期阶段，在图1(a)中，在煤矿采空区形成的初始阶段水动力循环交替作用较强，采空区内水位较低且氧气充足，常呈现出氧化环境，此时采空区积水的水质演化除了与常规的溶解、沉淀、阳离子交换作用、(解)吸附作用相关还与氧气参与下的多种氧化作用相关。在这一阶段，原始含水层的地下水通过导水裂隙进入采空区形成积水，与采掘空间中无机介质[26-27]，如岩(煤)层、采掘器械、支护设备等，以及有机介质[28-29]，如腐植酸(HA)，各种机械使用的乳化液、润滑油等发生化学反应，导致某些特征离子发生氧化还原、交替吸附或溶解沉淀。而随着采空区内的水位不断回升，逐渐转变为缺氧环境，环境的变化控制着复杂的生物地球化学反应的类型及作用程度，从而影响采空区的地下水化学组分演化过程，如图1(b)所示，此时水动力循环交替作用减弱，逐渐影响水化学平衡的反应方向，导致采空区积水水质发生变化。在水化学场的作用下，一些特征组分呈现出“短期增加，长期减少”的趋势[30]。以硫酸盐为例，由于氧气含量的降低，采空区逐渐转变为缺氧环境，水–介质发生的水化学反应从以黄铁矿等氧化作用为主转变为以硫酸盐还原作用为主，水体内硫酸盐的增涨速度减缓甚至缓慢降低，这也可能导致水体的TDS 在达到平衡后缓慢降低[31]。

1.2.2 微生物作用

微生物场在自然界中的分布不同于水动力场和水化学场，一般情况下，系统内的微生物群落结构和丰度并不呈现出连续的梯度变化趋势。即便在同一系统中相邻的位置之间，微生物群落结构和丰度也可能差异较大，而产生这种差异的影响因素是复杂且多元的，例如，在煤矿区地下水环境中，相比于原始含水层的寡营环境，在采空区积水为有机物与能量供应相对充足的的富营养环境，微生物在这种条件下会快速生长繁殖，并在氧气、pH 及岩层物源条件的筛选作用下，微生物的群落结构和丰度会发生变化[32]。此时，原始含水层与采空区积水、采空区积水形成初期(有氧环境)与采空区积水形成后期(缺氧–厌氧环境”)中的微生物群落结构与微生物浓度差异很大的微生物差异很大，而氧气含量和微生物可利用的能源类物质的浓度即为影响微生物群落组成与丰度的主要影响因素。

在采空区封闭的初期即水位回升阶段，采空区内部处于有氧环境，好氧型微生物如硝化细菌、硫杆菌和铁氧化菌等比例增加[33-34]。硝化细菌在氧气充足的条件下会将 NH-4转化成 NO-3和 NO-2[35]。硫杆菌和铁氧化菌等将含硫和铁的矿物氧化[36-38]，硫、铁氧化物水解于矿井水中形成 SO24-、Fe2+、Fe3+[39-40]。采空区封闭后逐渐被矿井水充满过程中，由于人为扰动停止，水动力条件逐渐趋于稳定，使得矿井下微生物丰度及多样性增加和迁移扩散的趋势停滞，其溶解氧(DO)、pH 值、氮源、碳源等物源环境发生改变，有氧的氧化环境逐渐转变为缺氧或厌氧的还原环境[41]。在此环境下，微生物群落种类、活跃程度及数量发生变化，厌氧型反硝化菌、铁还原菌、脱硫菌等比例增加[40,42-43]。在还原环境下，采空区积水水质中的反硝化菌可将NO和 NO反硝化生成N2[44]。有机物厌氧降解菌可将采空区积水中硝基苯、多环芳烃(PAHs)、石油烃、氯苯等有机污染物降解为代谢物及CO2[45-46]。铁还原菌可将Fe3+还原为Fe2+[22,47]。而脱硫菌可利用有机碳等碳源的生化降解过程中产生的ATP 和高能电子将采空区积水中的 SO还原为S2–，造成水中H+的消耗，使得采空区积水碱度增加，并形成气态硫化物H2S 逸出或金属硫化物FeS 沉淀，从而改善了采空区积水的水质。

2 水动力驱动的关键参数计算模型

通常情况下，水动力场主要是通过水头、水量、流速的改变来驱动水质演化，其作用强度与直接充水含水层的富水性、介质渗透性能及流体的运动性能相关。对于地下水而言，其自身的运动性能取决于黏滞系数和容重，2 者大小和温度密切相关，但根据前文所述，研究区水文变化幅度较小(25～28 ℃)，对于地下水的黏滞系数与容重影响较小，2 者均可视为定值。因此，在深部矿井的采空区，影响其水动力条件的关键参数为采动裂隙发育特征及直接充水含水层富水性能共同控制下的涌水量和渗透系数，且根据煤层实际的开采方式，这些关键参数在采空区以垂向和开采推进方向的二维变化为主。

2.1 渗透系数

由于采空区裂隙带与垮落带的岩石破碎程度不同，2 者的渗透性存在明显差异，并且在实际采空区中，各岩层的孔隙渗透性能要远低于采动裂隙[48]，因此本文数学模型忽略采空区裂隙带与垮落带岩层中的孔隙。

针对岩石较为破碎的采空区垮落带，多将其视为由粒径为Da(一般取值为0.25～1.00 m)的岩石颗粒所组成的均匀介质，根据Blake-Kozeny 公式[49](式(1))可计算采空区垮落带中的渗透系数:

式中,K为岩层渗透系数，m/s；n为岩层的空隙率(有效孔隙率和裂隙率之和)；Da为岩石颗粒的平均粒径，m；γ为流体容重，N/m3，这里取10 kN/m3；μ为流体动力黏滞系数，N·s/m，这里取1 000 N·s/m。

由式(1)可知，在垮落带破碎岩体的粒径一定的情况下，其渗透系数与空隙率成正比。由于岩层垮落和破坏后产生体积碎胀，导致采空区部分储水空间被碎胀体积所占据，破碎岩体的空隙率可以用碎胀系数表示(式(2))[50]，而采动产生的裂隙空间随应力恢复而逐渐压密，使得采空区垮落岩体的碎胀系数处于动态变化中。结合文献[51]给出的垮落带碎胀系数的计算公式(式(3))，可得到垮落带空隙率的计算公式(式(4))。

式中，n0为垮落带岩层的空隙率；nρ为岩层原始有效孔隙率，指有效透水的孔隙体积与原岩体积之比，深埋基岩的有效孔隙率取值一般较小，可忽略；kρ为裂隙带第i层上边界的碎胀系数；kρ0为垮落带碎胀系数；为垮落带初始碎胀系数，根据文献[52]，取经验值1.5；E0为初始切线模量，MPa，其取值与岩体的单轴抗压强度及初始碎胀系数相关[51]；σ为垮落带岩体承受载荷，与裂隙带高度和煤层埋深相关[53]，MPa。

裂隙带不同高度的空隙率、碎胀系数与距离开采煤层的间距的关系一般通过式(5)表示。为了进一步的分析，笔者将采空区裂隙带的岩层分成x层，如图2 所示，且每层岩石的平均碎胀系数为该岩层的下边界碎胀系数，结合式(2)、(5)和Blake-Kozeny 公式[54](式(6))，进一步推导出采空区渗透系数表达式(式(7))，其中裂隙带下边界碎胀系数和衰减系数η在采动停止以后的变化均较小可视为定值，因此采空区裂隙带渗透系数主要与开采煤层的间距相关。

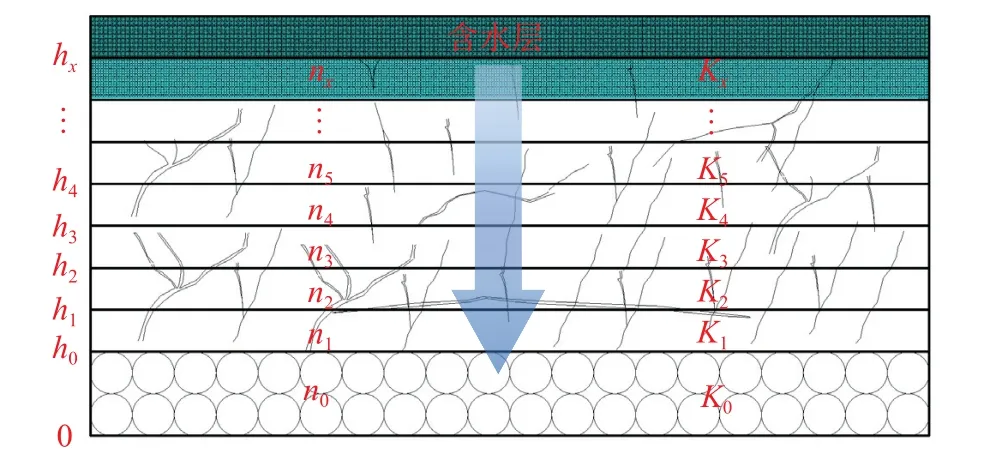
图2 水位回升阶段采空区水动力场概念Fig.2 Hydrodynamic field of water level recovery stage

式中，K0为裂隙带下边界的垂向渗透系数，m/s；kρi为裂隙带第i层上边界的碎胀系数；kρ′为裂隙带下边界的碎胀系数，根据文献[52]，取经验值1.15；η为垂直方向体积碎胀系数衰减系数，通过实测垮裂带高度反算求得；h0为采空区裂隙带下边界、垮落带上边界的高度，m；hi为第i层岩层顶板距离采空区底板的高度，m；n′i为第i层岩层的空隙率。

将鄂尔多斯矿区某煤矿3103 工作面采空区的埋深、岩石力学性质等参数的实测值及经验值代入式(7)中的计算模型中，可绘制采空区渗透系数的垂向变化曲线，如图3 所示。

图3 采空区渗透系数的垂向变化曲线Fig.3 Vertical change curve of permeability coefficient

由图3 可知，采空区的渗透性能随高度的增长呈指数级减弱，这是由于裂隙带内的岩体与垮落带相比较为完整，在垮落带上部有序的排列堆积。裂隙带岩体与煤层距离越远，受到的采动影响程度越小，其破碎程度也越低。

2.2 水位回升高度及交换水量

根据第1 节分析，单一顶板充水含水层的封闭采空区的水动力场流动路线可以简化为水位回升阶段和蓄满水量交换阶段。在第1 阶段，随着水位的回升，氧气含量、岩层物源条件等变化引起的水–岩作用及微生物作用类型改变，从而引起水质改变，因此在第1 阶段水质影响的主要控制参数是时间和水位高度；而在第2 阶段，采空区积水中的氧气被基本耗尽，物源条件也不再发生变化，且由于积水与顶部原生地下水发生水量的长期交换，水体内部反应由水–岩作用为主转变为以水–水作用为主，进而导致水质变化。因此，第2 阶段水质变化的主要控制参数是流经采空区的水量。

2.2.1 积水水位回升阶段

通常，采空区水位回升阶段的流量可以利用大井法[55]计算(式(8))，结合式(2)、(3)、(5)可得采空区水位恢复时间t与高度z的关系(式(9))。

式中，Qr1为第1 阶段流入采空区的流量，m3/s；Ka为顶板含水层的渗透系数，m/d，通过式(7)求得；M为含水层(出水段)厚度，m，实测值为11.50～79.97 m，取35 m；S为降深，m，实测值为682.83 m；R0为含水层的引用补给半径，m；r0为引用半径，m；t为采空区水位恢复至高度h所需时间，d；hx为采空区高度，m；A为采空区面积，m2；tz为采空区水位恢复至裂隙带顶板所需的总时间，s；tk为水位由煤层底板恢复至垮落带顶板所需的时间，s；tl为水位由垮落带顶板恢复至裂隙带顶板所需的时间，s。

将参数代入式(8)、(9)后，计算得Qr1=926.5 m3/h，并绘制采空区水位高度随时间的变化曲线，如图4所示。

图4 采空区水位高度随时间的变化曲线Fig.4 Change curve of goaf water level with time

由图4 可知，采空区垮落带内的水位回升高度随时间呈线性变化，这是由于计算模型中假定垮落带有相同粒径岩石所组成的均匀理想介质，其空隙率为常数，且由于采空区储水量受岩石空隙率控制，导致空隙率较低的裂隙带内水位回升速度明显快于垮落带。

2.2.2 蓄满水量交换阶段

采空区蓄满后，由含水层流经采空区的水渗流路径为含水层上游→裂隙带→垮落带→裂隙带→含水层下游。现将流经采空区的水量按流动路径的通道性质进一步分解为3 段，如图5 所示。即采空区上游沿采动裂隙带进入采空区的水量(QR)、沿着垮落带通道从采空区上游流向采空区下游的水量和采空区下游沿采动导水裂隙流出采空区进入下游含水层的水量(QC)。则此时采空区水动力场可以概化为两端为裂隙带通道，中间为垮落带通道的渗流模型。其中由于垮落带空隙率远大于裂隙带为强过水通道，地下水在第2 段渗流路径产生的水头损失可以忽略不计，因此，地下水流经采空区的渗流路径可以进一步等效为地下水穿透弱—强—弱3 个渗透能力不同岩层的渗流，整体渗流路径的两端均受到渗透能力较弱裂隙带的控制。裂隙带岩层垂向渗透能力强弱取决于顶板上方渗透系数最小的分层，也就是说上部含水层的水通过顶板覆岩渗流到采空区的垂向透水能力取决于采动破坏后裂隙岩体中隔水性能最强的岩层。忽略各岩层自身的孔隙率，采空区各岩层渗透性能主要与开采煤层的间距及上覆载荷相关。因此，对于岩石力学性能基本相同的采空区岩层而言，其垂向的渗透性能主要受采空区顶板渗透系数的影响。

图5 采空区蓄满阶段水动力场概念Fig.5 Hydrodynamic field of goaf filling up stage

水量交换阶段的渗流运动在含水层上下游水力坡度不大情况下可以近似的用达西定律描述。因此，结合地下水采空区关闭后顶部充水含水层上游地下水沿采动导水裂隙进入采空区的水量QR和采空区水沿采动导水裂隙流向下游含水层的水量QC分别为

式中，QR、QC为水量交换阶段流入(出)采空区的流量，m3/s；Kx为裂隙带最顶部的渗透系数，m/s；W为受采矿影响的含水层平面宽度，m；L为含水层渗流路径长度，m；H1、H3为采空区上(下)游含水层水头，m；H2为采空区底板水头，m。

在采空区水头稳定的情况下，含水层上游沿采动导水裂隙进入采空区的水量等于沿采动导水裂隙渗流入下游含水层的水量和上游流经采空区然后再进入含水层的水量[11]，因此这一阶段流经采空区的水量Qr2为

由于鄂尔多斯矿区某煤矿顶板直罗组砂岩含水层水位实测标高1 274.65～1 296.80 m，表明采空区所处地层较为平坦，采空区上下游水力坡度较缓，故取采空区上下游含水层平均水头差ΔH=15 m，将其代入式(12)，计算得Qr2约为128.25 m3/h。

2.3 模型验证

由于采空区封闭以后可测性较差，难以对采空区裂隙发育及流场演化进行长期观测，因此，本研究利用相似材料模型试验和室内三维箱式模拟试验相结合的方法对采空区裂隙发育情况及封闭以后水位回升过程进行模拟，并利用试验模拟的测试结果与第2节中的计算模型进行对比，以验证计算模型的可靠性。

2.3.1 模拟试验

(1)相似材料模拟试验。

笔者以鄂尔多斯矿区某煤矿某3-1工作面为地质原型，对于3-1煤工作面来说其主要的充水水源是顶板砂岩裂隙水，根据勘探资料显示，该工作面顶板岩性为粉砂岩、细砂岩、砂质泥岩、2 煤、中砂岩和泥岩。通过相似材料模型试验对该工作面采动条件下覆岩裂隙率的分布特征进行研究，进而分析其渗透性的垂向变化规律。以几何相似比CL=100:1、容重相似比Cγ=1.67:1建立相似材料模型。图6(a)为模型采高4 cm、推进距离为150 cm 时的采空区形态，此时采空区垮落带高度约为16.5 cm，裂隙带高度为71～75 cm。

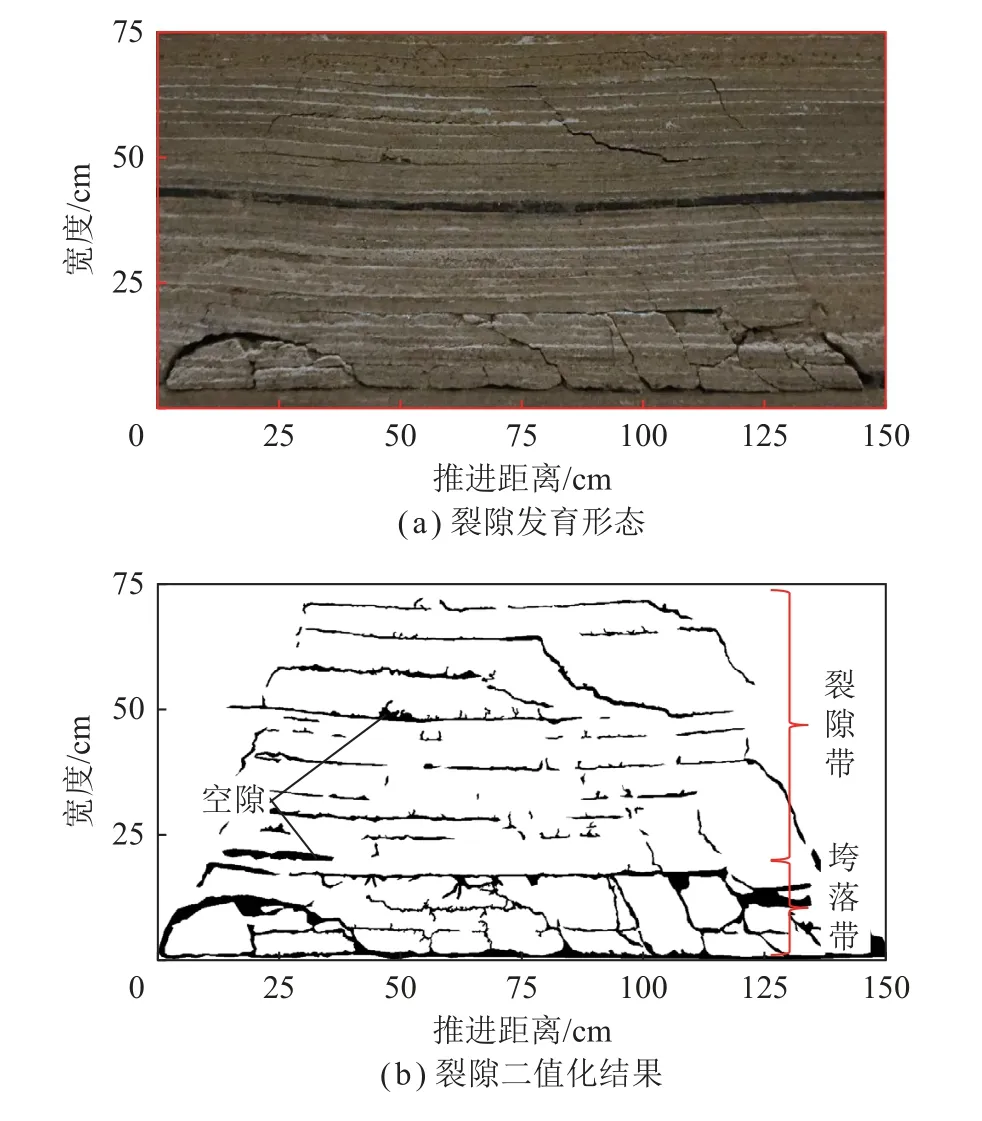
图6 相似材料模型试验中采空区裂隙发育形态及裂隙二值化结果Fig.6 Goaf and fissures formed and binarization of fissures in similar material test

本文相似材料模拟实验过程中采用单反相机记录采空区裂隙岩体发育过程，记录图像含有大量的色彩信息且含有多种噪声污染(常表现为孤立像素点或像素块)，直接利用会影响裂隙特征提取，对后期裂隙长度、宽度、空隙率等参数的计算产生误差。为进一步定量分析采空区垂向裂隙的变化规律，也为阐明垮落带和裂隙带不同高度渗透性演变规律提供基础，对相似材料模拟试验的照片进一步进行以下图像处理流程即可实现试验记录图像的裂隙特征的快速提取。

① 对于试验记录图像，首先可根据式(13)将图像3 个通道(RGB)转换成1 个通道，即灰度化处理。

② 将灰度处理后图像的每个像素替换为该像素周围像素的均值，这样就可以平滑并替代那些强度变化明显的区域，以实现图像的滤波降噪。

③ 将前处理好的灰度去噪图像通过图像分割进行二值化处理，使其变为只含有2 种颜色的图像，图像中黑、白2 种颜色分别代表裂隙和岩体(其中由于2 号煤层颜色与裂隙相近，该部分为人工调整结果)。

处理结果如图6(b)所示，可准确统计获取采空区不同高度空隙和完整岩层的像素面积之比，进而计算获取不同高度的采后空隙率，见表1。

表1 采空区不同高度空隙率统计计算结果Table 1 Statistical calculation results of fracture rate of goaf at different heights

由表1 分析可知：

① 在煤层顶板向上约16.5 m 范围内属垮落带，垮落体较为破碎，此区域空隙率约为22.25%，空隙率明显高于裂隙带和原始地层；

② 垮落带上部为裂隙带，此范围内空隙率相较于垮落带明显变小，且裂隙带范围内自下往上空隙率由0.5%逐渐增大至16.9%，同样显著高于原始地层。

(2)室内三维箱式模拟试验。

室内三维箱式模拟试验以采空区的垮落带和裂隙带为地质原型，此区域整体均为采空区填充物及部分上覆岩层，由上到下分别为较完整岩层、破碎岩层、块状矸石、煤泥等，各层厚度、岩性和空隙率根据实际前述实测及表1 中的相似材料模拟试验的统计、计算结果确定。如图7 所示，模型试验装置(模型箱)内径长度150 cm×宽度75 cm×高度75 cm，模型几何相似比为CL=100:1，模拟实际区域高72.5 m×宽75 m×长150 m长方体空间，该空间高度与实际采空区相同，底面积为实际采空区(面积约为8×105m2)的一部分。由于模型采用真实地层岩样和含水层水样搭建，模型容重相似比Cγ=1:1 。模型时间比Ct=:1=10:1，根据实测实际采空区的稳定涌水量约为900 m3/h，根据相似理论计算得模型注水流量(模拟稳定涌水量)约为2.1 mL/min。

图7 室内三维箱式模拟试验设计Fig.7 Schematic diagram of inflow and goaf in the simulative box

模型运行后，水位回升高度与时间的关系如图8所示。图8 中裂隙带的水位回升速度明显快于垮落带，且随着裂隙带高度的升高，水位回升速度呈现增快的趋势，这是由于空隙率随岩层高度逐渐减小，导致水位回升的过程中储水空间不断减小，在涌水量稳定的情况下，水位回升速度不断加快。

图8 模型试验中采空区水位高度随时间的变化Fig.8 Curve of goaf water level with time in the simulative box

2.3.2 试验结果与理论计算对比

计算结果与模拟试验实测结果(已进行相似比换算)进行对比，如图9 所示。图9(a)中，渗透系数K的理论计算和试验实测误差约为13.2%，表明理论模型计算与模拟试验的渗透系数基本为同一数量级，均是随着距离煤层距离的增加急剧下降，尤其裂隙带部分渗透系数呈数量级倍数的减小；图9(a)中，采空区水位回升高度随时间的变化曲线的理论计算和试验实测误差约为22.5%，理论计算的裂隙带水位回升速度明显快于垮落带，呈指数级增长，相比于试验实测，主要表现为垮落带水位回升更为缓慢，而裂隙带反之。总体蓄满时间误差约为3.4%，计算结果与实测值基本吻合，说明本研究提出的采空区水动力场关键参数的理论计算模型具备一定的可靠性。

图9 模型计算结果与模拟试验观测值对比Fig.9 Model calculation results and the simulation experiment observation

误差产生的原因是主要是由于理论模型计算的垮落带和裂隙带岩层的初始碎胀系数为经验值而非实测值，这导致理论模型的垮落带孔(裂)隙率计算值偏大而裂隙带孔(裂)隙率计算值偏小，同时理论模型未考虑各岩层的岩石力学性质的变化以及岩层本身的孔隙度，这些因素均会导致误差的出现。

3 水动力场的驱动作用及数学模型

3.1 水质演化的多场作用关系

对于水化学场、微生物场与水动力场之间的耦合，地下水流携带微生物和特征组分迁移，地下水流速越大，流体动压促使微生物及特征组分迁移越快；而微生物通过降解代谢、生长繁殖或消亡，特征组分通过溶解沉淀等作用引起渗流介质的孔隙度、孔喉大小与运移路径长度的变化，从而改变介质的渗透性能，间接控制地下水流速，但是相比于开采扰动形成的采动裂隙，这种通过生化作用对地层渗透性能的影响较小，因此在多场耦合的模型建立过程中可以忽略水化学场、微生物场对水动力场的反向耦合作用。

3.2 水动力场的概念模型

根据前文分析，采空区内的水动力场可以近似的看作顶部存在含水层入渗补给的非饱和无压渗流模型，可用Richards 方程表示，由含水率的计算公式(式(14))可知，此时的渗透系数不在是常数，而是与空隙介质的含水率相关。对于相似材料试验模拟的采空区而言，其整体的平均空隙率为9.86%，且研究区岩层相对于土壤或砂砾其致密程度较高，可以忽略其岩层本身的孔隙率。采空区裂隙岩层中粗糙裂隙面的间隙形成的开度分布与多孔介质固体颗粒间形成的喉颈孔隙分布的持水机制有一定的相似性。近似将采空区的煤(岩)体看作具有不可压缩固体骨架的多孔介质体，故可借助多孔介质渗流力学理论模型求解饱和–非饱和采空区介质中的含水率、压力水头等的时空分布情况。

式中， θ为采空区岩层的含水率；Sw为饱和度。

3.3 水动力场的数学模型构建

根据上述假设，采空区积水的过程即可以概化为顶部存在入渗补给的非饱和多孔介质渗流模型，以多孔含水介质的空隙表示采动形成的裂隙，并且忽略介质和流体的各向异性。因此，采空区水动力场模型的数学方程式为

式中，u为地下水渗流速度场，m/s；ρw为水的密度，kg/m3，这里取1 000 kg/m3；Qw为源汇项，m3/s。

忽略采空区积水的密度变化，以含水率表示积水连续运动方程为

将渗流速度场的公式(式(17))代入式(16)可得到采空区积水过程的饱和–非饱和数学方程，如式(18)所示：

式中，K(Sw)为饱和–非饱和渗透系数，m2/s，当饱和度较低时，采空区多孔介质中较大的孔隙没有充满水，此时渗透主要在较小的孔隙中进行，导致渗流作用的过水断面减小，渗流路径增长使相对值渗透率大幅减小，随着含水层的不断补给，采空区逐渐变为饱和状态状态，此时各岩层的渗透系数恢复为仅与空隙率相关的参数；p为压强，Pa，在饱和带p代表水的压强，取正值，在非饱和带中p代表毛管压强，取负值；z为以采空区顶板为垂向的零点垂向坐标，m。

(1)模型初始条件。

为简化起见，假设采空区同一水平剖面上初始空隙率是均一的，故渗透系数主要为垂向变化，因此有方程(式(7))，将其转变为空隙率初始条件的方程形式(式(19))。假设采空区同一水平剖面上初始含水率也是均一的，并且整个采空区初始为疏干状态。因此可认为除了顶部边界外，采空区任一高程的初始含水率均为0(式(20))。

(2)模型边界条件。

模型上边界为含水层入渗补给边界，且模型顶部渗透性较低，根据“大井法”可知，此时的入渗流量和顶部边界的渗透性相关。因此当采空区封闭以后，开采扰动停止其渗透性几乎不变的情况下，可以将采空区模型的上边界近似的概化为有稳定流量的入渗边界，即

式中，Q0为采空区顶边界的入渗流量，m3/d。

采空区顶部边界与含水层底板的接触面达到接近饱和的含水率，即Sw=1，结合式(13)有

再将n的表达式(式(19))代入式(6)～(16)即可得到采空区顶部的边界条件：

随着时间推移，采空区形成积水且水位不断升高，底板为较为完整的岩层，可近似假定为不透水边界，即下边界的流量等于0 的边界有

式中，hp为压强水头，m。

3.4 水动力场对水质演化的驱动作用

在关于地下水中特征污染组分形成与演化的研究中，水动力场多是以单一变量的形式研究其对特征污染组分的迁移和空间分布的影响。在实际的煤矿采空区中，是通过包括水动力场、水化学场、微生物场在内的多场共同作用对特征污染组分的形成、演化、迁移、分布产生影响的。

采空区封闭后，虽然人为扰动停止，但是此时的区域水动力场与原生水动力场已经存在明显差别，此时采空区成为了区域地下水汇水区域，导致地下水流速、物源条件、微生物群落与丰度的变化，从而引发了一系列水–水混合、水–岩(煤)作用以及微生物分解等作用，导致地下水质发生改变。在采空区蓄满后，在水动力场作用下，采空区积水会随着区域地下水渗流方向运移，导致采空区水与原生地下水不断发生水量交换，某些特征污染物被不断稀释，直至完全恢复至区域地下水的原始浓度。在水化学场控制方程(式(26))和微生物场的控制方程(式(27))中，其弥散项、对流项以及渗流源汇项均与水动力场密切相关，而生化源汇项则与氧气、pH、矿物成分以及微生物群落组成与丰度等因素相关。这表明水质形成与演化的多场作用是以水动力场为主导的，即水动力场对采空区积水的水质演化起驱动作用。

式中,Cs为地下水中特征组分的质量浓度，mg/L；∇[θD∇C] 为水动力弥散相，D为采空区积水中 SO的水动力弥散系数，m2/s；u·∇C为对流相；vsCss为源汇项，vs为源/汇的渗流速度，Css为水动力源/汇中的特征组分质量浓度(即主要充水含水层水中的特征组分浓度)，mg/L；f1为特征组分生化源汇项，包括吸附解吸项、矿物氧化还原相、微生物分解相等，表示由吸附解吸、矿物氧化还原以及微生物分解等作用引起的该点特征组分浓度的变化，相关作用的数学模型构建将在后续论文中进一步阐述。

式中，B为地下水中的微生物量，kg/kg(生物/液体)；Bns为水相自由态微生物量，kg/kg(生物/液体)；DB为水中自由态微生物水动力弥散系数，m2/s；由于自由态微生物会趋向适宜的环境运动，因此微生物自身会产生抵抗或顺应水动力场方向的运动速度即为uB，m/s；u-uB为某点微生物在水动力场影响下的迁移速度，m/s；Bss为水动力源/汇中的微生物量，kg/kg(生物/液体)；A′为裂隙面积与岩层体积之比，m-1；Bs为附着在岩层裂隙表面的固相吸附态微生物量，kg/m2；f2为由于多种因素(包括生物代谢、产物抑制、竞争及非竞争抑制作用等)导致微生物的生长繁殖死亡而引起的水中及裂隙表面的生物量的变化项，相关作用的数学模型构建将在后续论文中进一步阐述。

3.5 水动力场主导下的多场耦合本构模型

根据上述数学方程，水动力场与水化学场、微生物场之间的耦合则分别通过指标(v，C)和(v，B)进行关联。水动力场驱动下的多场耦合本构模型如图10所示，其耦合方程为

图10 水质形成及演化的多场耦合关系Fig.10 Multi-field coupling relationship of water quality formation and evolution

式中，Cs为地下水中特征组分的质量浓度，mg/L；Cs0为特征组分的初始质量浓度，mg/L。fa为地下水流速与生物量之间的量化方程；fb为水化场中特征组分浓度与生物量生长抑制之间的量化方程；fc为水化场中特征组分浓度在无菌条件下与地下水流速之间的量化方程；Ks为地下水流影响下的特征组分的微生物降解系数。

4 讨 论

(1)采掘活动空间的顶板涌水是井工煤矿采空区积水的最主要来源，笔者讨论了单一顶板充水含水层的采空区积水水质形成及演化的水动力场驱动作用、关键参数计算及多场作用数学模型构建的基础问题。但在实际生产过程中，采空区的涌水水源还包括部分底板水，甚至地表水，同时工作面的倾角及控水构造分布也各有差异，这些因素均会对其水动力场产生影响，因此，适用于不同矿区采空区的水动力场概念及数学模型的研究值得更进一步的深入探讨。

(2)采空区水质形成及演化的多场作用是以水动力场为主要驱动力，水化学场、微生物场协同参与的复杂过程，限于篇幅，多场耦合作用中的化学场、微生物场作用的数学模型构建将在后续论文中陆续阐述。

(3)多场耦合作用数学模型建立过程中，由于水化学场、微生物场对水动力场的反向耦合作用较小，本文暂时予以忽略。在少数极端环境下，此反向耦合作用较为明显时，需通过开展多种微观、宏观试验，对水动力–水化学–微生物场多场参数进行精准的动态观测，明确反向耦合作用的关键参数及驱动机制。

(4)现有针对多场耦合理论研究尚处于耦合机理研究以及数学模型构建阶段，其中大量的多场作用参数难以通过室内、室外试验确定。而现有的多场耦合模拟软件对水动力场、水化学场、微生物场参与下的矿井水水质形成与演化的模拟方案针对性不足，需进一步针对不同场景对各场参数进行精准调控，优化模拟方案，以提高研发不同场景下多场耦合模型的效率。

5 结 论

(1)阐明了煤矿采空区积水形成的水动力场演化机制，根据水动力场流动路径的差异将其分为水位回升阶段和采空区蓄满水量交换阶段；在此基础上，通过文献综述，探究了不同阶段的水动力场驱动下水化学场及微生物场的作用机制，揭示了采空区水质形成及演化的以水动力场为主要驱动力，水化学场、微生物场等多场协同作用的复杂过程。

(2)提出了采空区积水水质形成与演化的水动力场水位回升阶段和采空区蓄满阶段的概念模型，建立了基于顶板导水裂隙带不同垂高空隙反演的分层渗透系数定量计算模型，为开采扰动后采空区积水水位回升及蓄满后水量交换的计算奠定了理论基础。

(3)通过相似材料模型试验和室内三维箱式模拟试验对采空区裂隙发育情况及封闭以后水位回升过程进行了模拟，试验观测结果进一步揭示了采空区各层位空隙度具有垂向差异，并利用试验的实测数据与模型计算结果进行对比，理论计算渗透系数K和采空区水位回升高度随时间的变化与试验实测误差分别约为13.2%和22.5%，验证了计算模型的可靠性。

(4)在煤矿采空区水动力场以及水动力场影响下的水化学场和微生物场的控制方程的基础上，进一步明确了水动力场–水化学场–微生物场之间的关联指标和耦合关系，构建了以水动力场主导下的多场耦合的本构模型，可为进一步探究水动力场耦合驱动下的煤矿矿井水水质形成及演化规律的多场耦合模型构建提供启示。