基于Wray-Agarwal 湍流模型的鼓泡流化床气固流动的模拟研究与分析

乔红旺 宋钊毅 向 阳

(北京化工大学 化学工程学院, 北京 100029)

引 言

随着现代工业的快速发展,人类社会对化石能源的过度依赖造成了一系列的生态环境问题。 在碳中和背景下,亟待开发清洁能源。 太阳能具有清洁、存量巨大等特点,是一种非常理想的清洁能源。 太阳能的开发利用需要太阳能电池板,其主要材料是高纯度的多晶硅。 现阶段多晶硅生产主要采用第三代西门子法,但硅烷流化床法具有结构简单、能耗低等优点,是多晶硅产业未来发展的重要方向。 然而,流化床反应器内气固两相流体力学特征与气相沉积反应动力学都很复杂,现有研究还远远不够充分,需要更加深入的探讨[1-2]。

近年来,随着计算机技术的快速发展,计算流体力学(CFD)得到了更为广泛的应用,在获得实验中难以测量的详尽参数、阐明过程机理的同时,又大幅度降低了科研成本,安全性更高。

气固流化床内多相流动是一种非常复杂的湍流流动,目前应用广泛的k-ε和k-ω两方程模型被用于反应器数值模拟研究。 Mehdizad 等[3]基于Shear Stress Transfer(SST)k-ω模型建立了一种新的数值模型,使其能够在广泛的颗粒直径和颗粒密度范围内研究气固床中的最小流化速度。 Du等[4]选择Standardk-ε湍流模型研究了多晶硅流化床反应器中多晶硅颗粒的生长过程。 Wu 等[5]用Realizedk-ε模型探究了多级流化床的气固流动特性。 2015 年,Wray 和Agarwal[6]在两方程的基础上提出了一方程模型,即Wray - Agarwal(WA)湍流模型,并在单气相流动模拟中获得了成功。 Han 等[7]在WA 模型的基础上提出了一种新的分离涡模型,并应用于壁面有界分离流动的模拟中,结果表明新提出的模型与实验结果吻合较好。 相对于单相流,多相流的流型复杂多变、相间相互作用强,数学描述难度更大,且计算负荷高。WA 模型对旋流和复杂壁面条件进行了优化,它在复杂流动条件下具有效率高、 成本低、精度高、收敛性好等优点。 Hu 等[8]在旋转填充床中引入WA模型描述气液流动,基于文献的持液量和数均分子量数据验证了模型的有效性。 Tang 等[9]、Liang等[10]将WA 模型应用于方形鼓泡塔模拟气液的运动,模拟结果与实验数据吻合良好。 Shao 等[11]首次将WA 模型应用于循环流化床立管的气固流动模拟中,结果表明,WA 模型能够很好地预测立管上部的颗粒分布,但不能很好地预测立管下部的颗粒分布。 在大部分区域WA 模型对颗粒浓度和质量通量的径向分布的预测总体上优于常规模型,但在中心部分仍存在预测过高的问题。

本文根据气固两相流动特征,将WA 湍流模型应用于鼓泡流化床的模拟研究,并将其与Standardk-ε模型和SSTk-ω模型进行对比分析,验证WA模型的可靠性及适用性,为WA 模型进一步应用于化学反应器内多相流动提供一定基础。

1 数值模拟方法

1.1 几何模型及网格划分

基于Dubrawski 等[12]的实验,本文建立流化床的三维物理模型。 如图1 所示,反应器分为流化段和扩展段。 流化段直径0.133 m,高0.96 m;扩展段直径0.19 m,高0.4 m。 由于真实的流化床入口分布器结构比较复杂,为网格划分和数值模拟带来了一定困难,所以本文将流化床底部简化为一个均匀进气的圆面,根据模型在ICEM 中进行了反应器的建模与结构网格的划分。

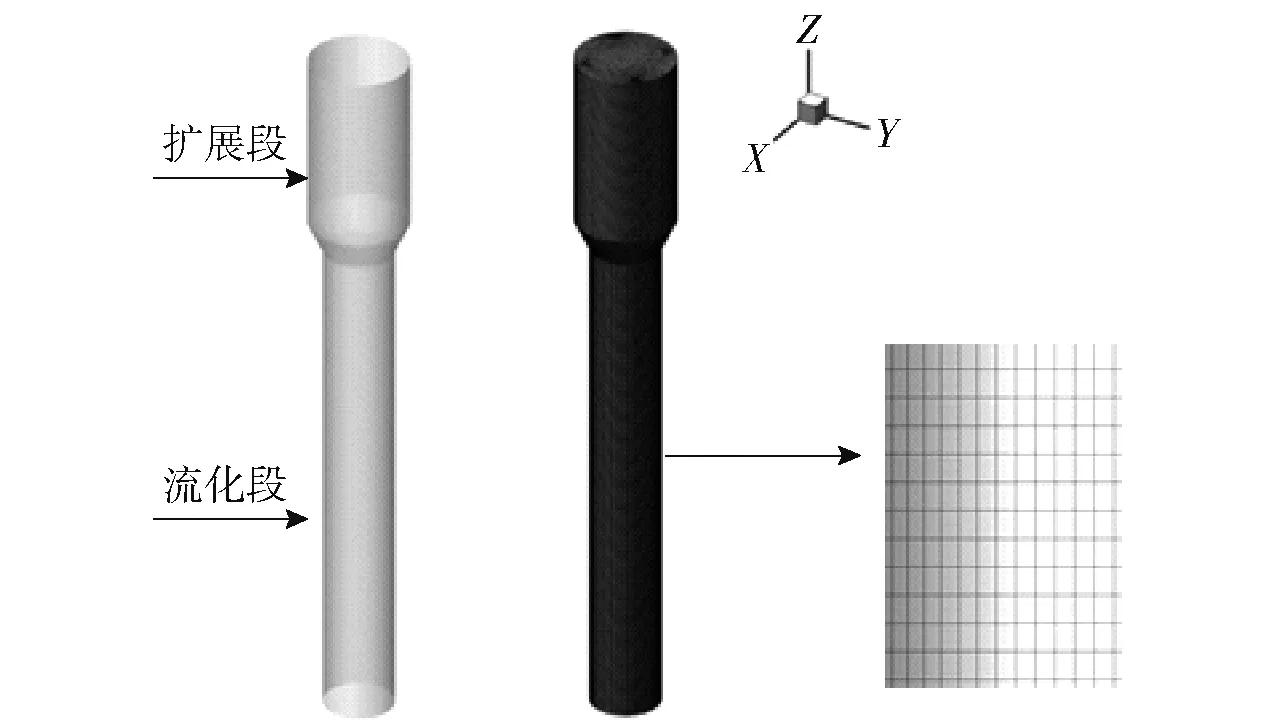
图1 几何模型及网格划分Fig.1 The geometric model and meshing

1.2 网格无关性验证

为了获得与网格无关的计算结果,本节共生成了29 100、43 008、92 880、226 600 和366 000 这5 个数量的网格,并探究了其对床层压降的影响。图2 为床层压降随网格数量的变化,从图中可以看出当网格数量达到92 880 时,床层压降便趋于稳定,综合考虑计算成本和精度,后续都采用此网格尺寸。

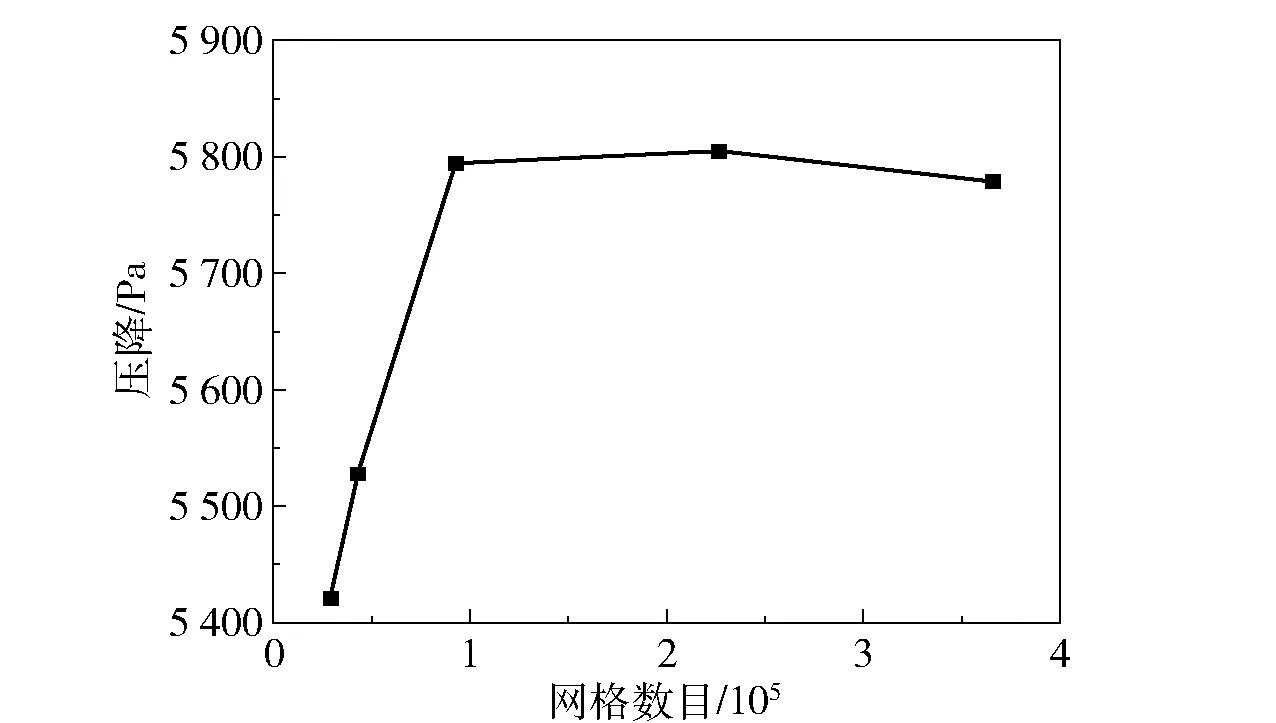
图2 网格数目对床层压降的影响Fig.2 The effect of grid number on bed pressure drop

1.3 数学模型

1.3.1 基本控制方程

本文采用基于欧拉-欧拉方法的双流体模型(two-fluid model,TFM)来进行鼓泡流化床中气固两相流动的数值模拟研究,它将气固两相都看作连续相,守恒方程如下。

连续性方程

气相

式中:p为压力;Sv为非均相反应导致的动量变化源项;g为重力加速度;β为相间动量交换系数;τ为剪切应力张量。

1.3.2 颗粒动理学理论

双流体模型将颗粒相按照连续相来处理,颗粒动理学理论解决了如何描述固相黏度和压力的问题,使得双流体模型封闭。

颗粒相压力

式中:Θs为颗粒拟温度;enm为碰撞恢复系数。

颗粒相剪切黏度

式中:μs,col为颗粒相剪切黏度的碰撞项;μs,kin为颗粒相剪切黏度的动力项;μs,fr为颗粒相剪切黏度的摩擦项。

1.3.3 曳力模型

本文采用Gidaspow 曳力模型,它是Wen-Yu 曳力模型和Ergun 方程的结合,能对粗网格条件下的Geldart B 类颗粒进行准确的模拟。 模型方程如下。

当αg＞0.8 时,由Wen-Yu 模型给出

式中:k为湍流脉动动能;ω为比耗散率;Γ为有效扩散系数;D为交叉扩散系数。

3) WA 模型

Wray-Agarwal(WA)模型是基于k-ω模型导出的新的单方程模型,它将k和ω方程合并为一个R(R=k/ω)运输方程。

式中:v为运动黏度;ρ为流体密度。

式中:σR、σkε、σkω为湍流普朗特数。

湍流黏度由下式计算:

WA 模型运输方程中的模型常数取值如下:C1kω=0.082 9,C1kε=0.112 7,σkω=0.72,σkε=1.0,κ=0.41,Cω=8.54,Cm=8.0。

1.4 边界条件及求解方法

气相设置为空气,采用速度入口,设置整个圆柱底面均匀进气,速度0.4 m/s;出口为压力出口;壁面为无滑移壁面。 第二相固相设置为颗粒,其密度2 330 kg/m3,均一粒径103 μm。 固相的初始床层高度为0.8 m,体积分数为0.55。

本文所有的模拟计算均在ANSYS-Fluent 上进行,求解器设置为三维双精度,并采用多核心节点并行计算。 WA 湍流模型通过软件提供的接口,以用户自定义标量方程(User Defined Scalar,UDS)的形式添加到Fluent 中,其他模型参数等通过用户自定义函数(User Defined Function,UDF)的形式编译到软件中进行求解。 入口处R方程的值设置为1 ×10-5,壁面处R的值为0,出口处为0 通量。 同时为了保证计算过程的稳定收敛,R的松弛因子为0.2。求解时采用压力-速度耦合的Phase Coupled SIMPLE 算法,求解的时间步长设定为0.001 s,每个时间步的最大迭代数为40。 为了保证模拟结果稳定性,总共计算30 s,并取10 ～30 s 内的平均值来进行后续数据的分析。

2 结果与讨论

2.1 固含率分布瞬时云图

图3 为不同湍流模型模拟得到的床层固含率瞬时分布云图。 3 种湍流模型得到的床层的最大膨胀高度基本相同,整个床层的近壁面区域固相体积分数较大,这也是由于床层中的大气泡主要在流化床的中心处产生,使得近壁面的颗粒相对较多。 比较不同时刻下的切面固含率的瞬时分布云图可知,随时间的变化,流化床内呈现周期性大气泡的生长与破裂,符合实际工况,3 种湍流模型均可对气固流化床的流动进行模拟。

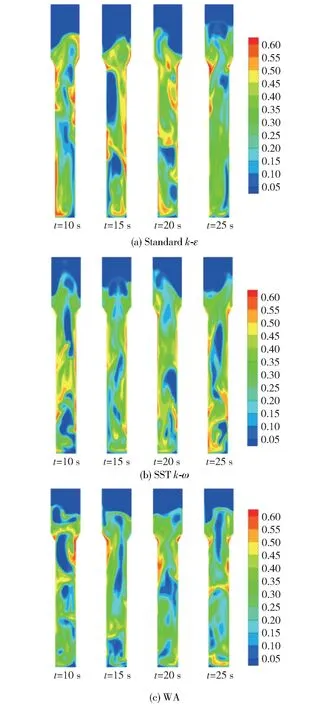
图3 3 种湍流模型的床层颗粒固含率瞬时云图Fig.3 Instantaneous cloud of bed particle solid holdup with three turbulence models

2.2 床层压降分布

在无内构件的空塔情况下,流化床的床层压降可由下式计算得到

式中:Δp为床层压降;H0为初始床层高度;ε0为初始床层空隙率。

图4 为不同湍流模型预测的床层压降随时间的变化规律。 由图可知,流化床在2 s 左右可达到稳定流化状态,压降随大气泡不断地生长与破裂呈现有规律的波动。 Standardk-ε和SSTk-ω湍流模型的模拟结果相差不大,绝大部分压降超过理论值;WA 模型则在理论值附近波动,其预测结果更准确。

图4 3 种湍流模型预测的床层压降随时间的变化Fig.4 Variation of bed pressure drop predicted by three turbulence models with time

表1 为不同湍流模型预测的平均床层压降模拟值与理论值的对比。 由式(26)计算得到的压降理论值为5 499.36 Pa,Standardk-ε湍流模型、SSTk-ω湍流模型和WA 湍流模型的预测值的相对误差分别为6.4%、8.6% 和1.6%。 结果表明,WA模型的预测值的相对误差更小,模拟结果更准确。

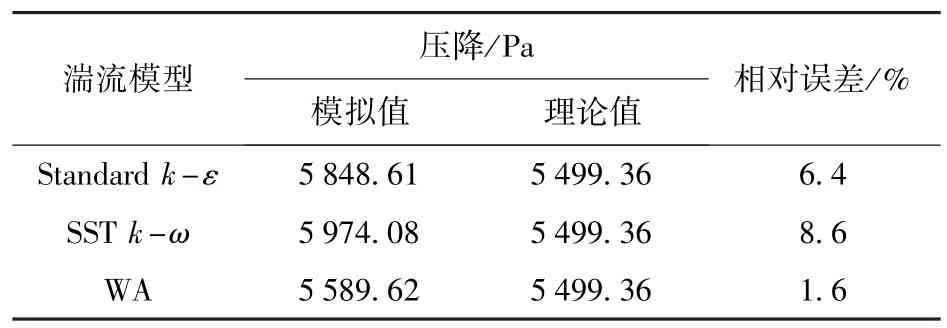
表1 3 种湍流模型预测的床层压降与理论值的对比Table 1 Comparison between simulated and theoretical values of bed pressure drop predicted by three turbulence models

表2 为采用不同湍动模型反应器内的平均湍动能。 由表可知,通过WA 模型计算的湍动能低于其他两种湍流模型的模拟值,导致床层压降模拟值稍小于其他两种湍流模型的计算结果。

表2 不同湍流模型的整体平均湍动能Table 2 Overall average turbulent kinetic energy of different turbulence models

2.3 轴向空隙率分布

图5 为3 种不同湍流模型模拟得到的轴向平均空隙率模拟值与实验值的对比图。 从图中可以看出,不同湍流模型的空隙率沿轴向高度的模拟结果规律相近。 SSTk-ω湍流模型的模拟值在流化床底部显示出与实验值更好的一致性,而WA 湍流模型在流化床的中部(0.75 m)附近表现出更好的一致性。 总体来说,3 种湍流模型均与实验结果吻合较好,均可对流化床的气固流动进行准确地模拟。

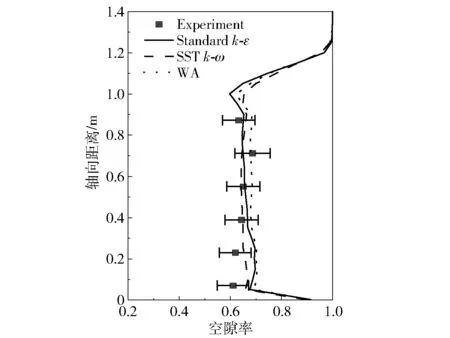
图5 轴向平均空隙率模拟值与实验值的对比Fig.5 Comparison between simulated and experimental values of axial average voidage

2.4 径向固含率分布

图6 为不同湍流模型在4 个轴向高度处的径向固含率分布模拟值与实验值的对比。 从图中可以看出,3 种湍流模型对于径向固含率的模拟结果的整体走势是相同的,都呈现一种中间低、两边高的对称分布特征,这与实验结果相同,也与2.1 节的固含率瞬时分布云图一致。

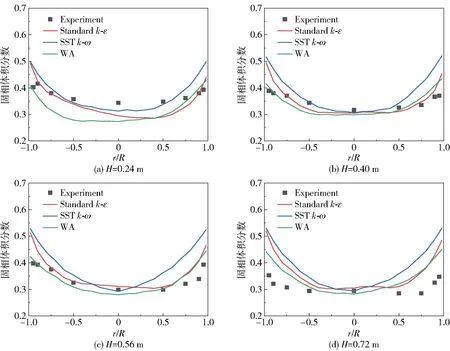
图6 3 种湍流模型在不同高度的径向固含率分布模拟值与实验值的对比图(ug =0.4 m/s)Fig.6 Comparison between simulated and experimental values of radial solid holdup distribution of three turbulence models at different heights (ug =0.4 m/s)

在流化床的底部区域(H=0.24 m),3 种湍流模型都低估了中心处的固相体积分数,而在壁面附近,WA 湍流模型与实验值更为接近。 在流化床的中部区域(H=0.40 m 及H=0.56 m),WA 湍流模型的预测值与实验结果在壁面处及流化床中心处均吻合较好。 在流化床的上部区域(H=0.72 m),3 种湍流模型对于径向固含率的预测趋势一致,在流化床中心处与实验值吻合较好,而在壁面附近都高估了径向固含率。

2.5 颗粒速度分布

颗粒速度在气固流化床流体力学特征的测定中起着重要的作用,本小节给出一些WA 模型的模拟结果。 图7 为颗粒轴向速度时均分布云图,图8 为不同床层高度处颗粒轴向速度的径向分布。 从图中可以看出,颗粒整体上呈现一种中间区域向上运动、近壁面区域向下运动的趋势。 这种流动规律与气泡的形成、运动和分裂有关。 由于边壁效应的存在,中心区域的阻力较小,带着颗粒的气泡在流化床的中心向上移动,移动到一定高度时,气泡破裂并释放出其中的颗粒,然后粒子在重力的作用下沿着壁面向下运动,从而形成稳定的流化状态,也导致了内部颗粒的非均匀径向分布。

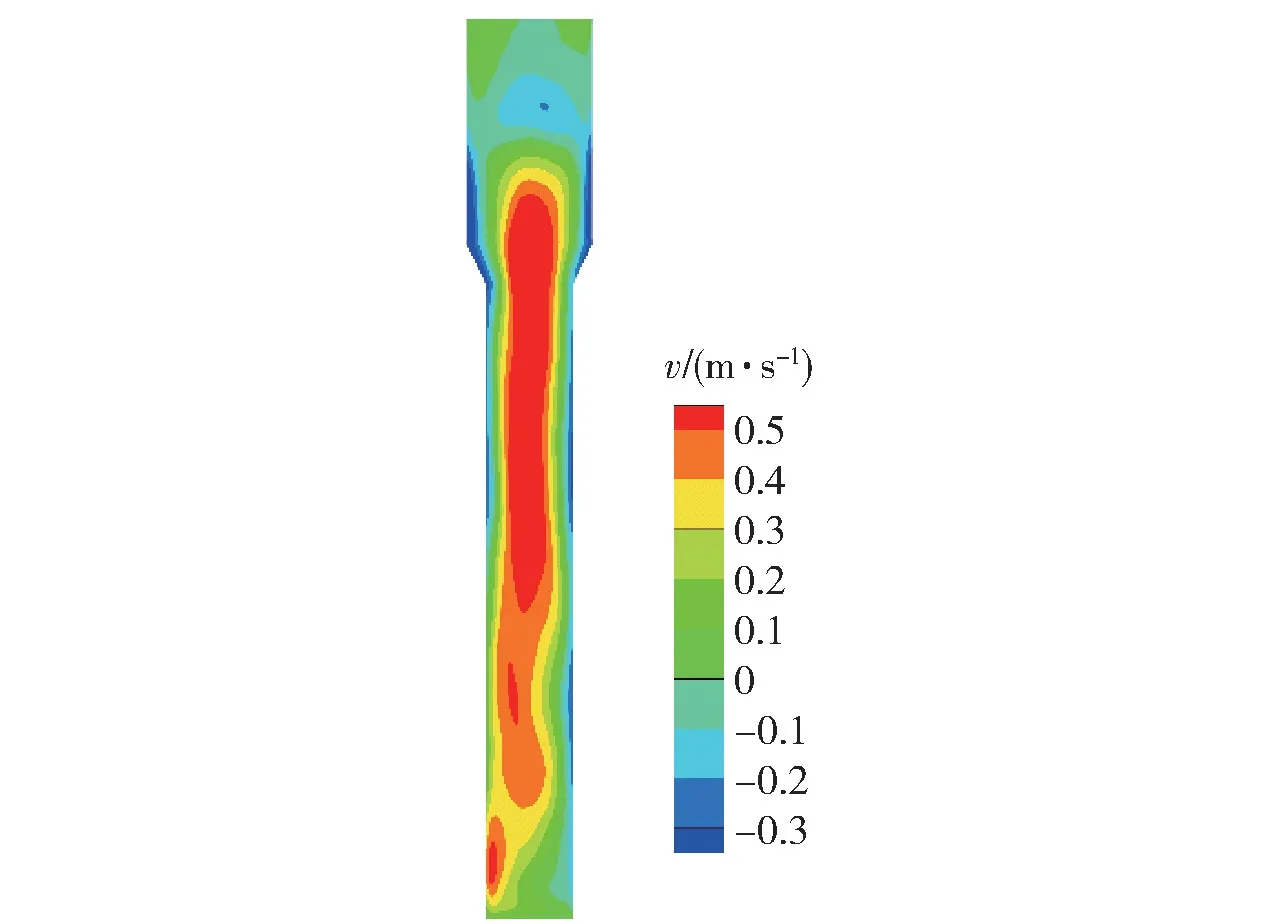
图7 颗粒轴向速度时均分布云图Fig.7 Time-averaged distribution cloud of particle axial velocity

图8 不同床层高度处颗粒轴向速度的径向分布Fig.8 Radial distribution of particle axial velocity at different bed heights

3 结论

本文成功地将WA 湍流模型应用于气固流化床流动的模拟中,并与经典的两方程模型进行对比,验证了WA 模型的可靠性与适用性。 结果表明:

(1)WA 湍流模型对床层压降的预测值与理论值的相对误差最小,仅为1.6%。

(2)通过对平均轴向空隙率的分析可知,3 种湍流模型的预测值均在误差允许的范围内,SSTk-ω湍流模型在床层底部与实验结果有更好的一致性,WA 湍流模型在床层的中部附近吻合得更好。

(3)通过对不同高度处平均径向固含率分布的分析可知,在流化床的中部区域,即H=0.40 m、H=0.56 m 附近,WA 湍流模型的预测值在整体上与实验值吻合最佳;在流化床的上部区域WA 湍流模型的预测值也比Standardk-ε和SSTk-ω湍流模型的预测值更接近实验值。