基于极轨卫星的贵州日最低气温遥感推算初探

杨士进,张明祥,彭 波,袁三明,李慧璇,廖 瑶

(1.贵州省气象服务中心,贵州 贵阳 550002;2.贵州省生态气象和卫星遥感中心,贵州 贵阳 550002)

0 引言

低温冷害是贵州常见的气象灾害之一[1]。低温能使茶树等作物受损,品质降低[2-3],每年造成的损失数以亿计,严重制约着贵州农业产业发展。因此,开展低温监测对作物区划、灾害影响评估及保险理赔等都具有重要意义[4-5]。低温是判断降温过程强度的指标[6],常规的低温监测是根据气象站在离地面1.5～2 m处观测的数据,依赖于台站的分布,对于无台站区域的数据则主要靠插值推算。目前常用的有样条、反距离、克里金、多项式等插值算法,不同插值算法的适应性不同,不同区域、不同季节得到的最优插值算法不同[7-8],通常距离气象站点距离越远,插值的误差就越大。由于贵州地形复杂,目前站网间隔大小不一,有的站间隔达11 km[9],不可避免会对插值结果产生影响。

卫星遥感具有覆盖广、时效性高等特点,成为地面观测的有力补充。常用的极轨卫星传感器能够提供高达1 km分辨率的热红外遥感数据,在无云覆盖的区域能够反演获得无缝的地表温度(LST)数据。地表温度数据可用于估算气温,常用的遥感气温估算方法在最低气温、最高气温和平均气温估算方面都有应用。气温是由地表温度间接影响的,因此可以由LST参数化推算而来[10],这是气温可以由地表温度进行估算的理论基础。常用的推算方案有简单统计法、高级统计法、温度植被指数法(Temperature-Vegetation Index,TVX)、能量平衡方法和大气温度廓线外推法等[11]。简单统计法利用地表温度参数进行气温估算,此法抓住地表温度这一影响气温的最主要矛盾,即可得到较好效果,其平均标准偏差达1.3～2.0 ℃[12-13],但也有研究表明在作物生长季平均标准偏差达到3.8 ℃[14]。高级统计法利用影响温度分布的地表类型、经纬度、高程等参数,构建多元回归模型进行气温估算,估算的旬平均最高气温、月平均气温误差在3 ℃以内[15-16]。研究表明,夜间地表温度和日最低气温的一致性最高[14],利用夜间地表温度和白天地表温度推算气温发现夜间地表温度的效果更好[17]。最初的温度植被指数法[18]利用地表温度和植被指数之间的负相关关系进行气温推算,只适用于浓密植被地区,对于有云、水体或植被稀少地区和复杂山地时误差较大,而通过去除窗口内云和水体可以扩大TVX算法的适用性[19]。能量平衡方法利用能量平衡方程对气温进行计算,涉及的参数计算众多,挪威中部、西部和东部的中低高山带与地面数据的决定系数>0.9[20]。大气温度廓线外推法利用遥感反演的大气温度廓线产品和海拔高程数据开展气温推算,采用NOAA或MODIS大气温度垂直廓线产品推算近地面气温的研究较多,误差多在3 ℃以内[21-22]。从以上研究来看,高级统计法物理及统计意义明确,模型复杂度相对较低,但也能获得精度较优的结果,具有较高的实用价值。但高级统计法建立的模型依赖特定地区,推广到不同时空条件下误差可能较大,在地形复杂的贵州地区缺乏效果验证。

本文以贵州省为例,通过分析MODIS地表温度、高程等参数和日最低气温的相关关系,建立复杂地形下的日最低气温推算模型,并对模型精度进行验证,以期为低温指数保险服务开展提供气象站点外的数据支持。

1 研究数据

1.1 数据

本文选取2016年2月10日1742个、2017年4月1日1581个、2023年1月31日1864个贵州省自动气象站小时最低气温数据作为日最低气温推算的气象站点数据(因每个日期具有有效数据的自动站数量不同,故每个日期选取的自动站数量有差异),站点类型包括国家站和区域站,分别代表冬季和春季数据,站点分布见图1。

图1 气象站点分布示意图Fig.1 Schematic diagram of meteorological station distribution

遥感数据选取2016年2月10日、2017年4月1日和2023年1月31日夜间过境的AQUA卫星上的MODIS传感器的L2级日数据作为LST数据源,空间分辨率为1 km,同时,还选取2016年2月10日、2017年4月1日和2023年1月31日L2级的MODIS水汽数据参与分析建模。

一般来说,高程对气温的分布具有重大影响,因而选取了ASTER DEM V2数据作为高程的数据源。

1.2 数据预处理

针对MODIS LST数据,采用NASA官方发布的MRT软件进行投影转换为等经纬度投影,将DN值转换为摄氏温度,并根据质量控制字段(QC_Night),只保留LST质量字段值为0、8、17、65、73、81的数据,这些质量字段代表没有受到云影响且反演误差<3 ℃的地表温度。同时,对于2017年4月1日前一晚的LST数据,发现西部的LST数据异常,主要表现为大多LST<0 ℃,且比较破碎不连续,考虑是受到云污染导致LST值偏低,所以将其剔除。

对MODIS水汽数据,除了采用HEG进行投影转换为等经纬度投影外,还将DN值转换为真实的水汽含量(单位:cm)。

气象数据的质量控制采取异常值剔除法,去掉小时最高、最低、平均温均为0 ℃的数据及最高温>50 ℃的数据,通过小时最低温数据计算得到日最低气温数据。

将高程数据重采样到1 km的空间分辨率,并计算全省的坡度、坡向和地形开阔度数据,用于后续建模分析。

将所有数据的坐标系统进行统一,并根据所有气象站点的坐标,提取相应位置所有遥感栅格数据的值,去除每种数据的无效值,2016年2月10日、2017年4月1日和2023年1月31日剩余的有效数据分别为1369个、780个和1864个。

利用高程数据,添加经纬度字段,通过GIS软件构建全省1 km分辨率的经度、纬度栅格数据。

2 日最低气温推算模型构建

本文采用多元线性回归方法开展贵州省最低气温推算。首先根据单因素相关分析,利用一元线性相关分析模型,分别得到所有要素和日最低气温的相关系数,筛选出线性相关性显著的要素。其中2016年2月10日线性相关性高的要素从高至低依次为地表温度、纬度、高程、经度(图2);2017年4月1日线性相关性高的要素从高至低依次为地表温度、高程、坡度、经度(图3);2023年1月31日相关性高的要素从高至低依次为地表温度、坡度(图4)。均通过0.01的显著性检验。

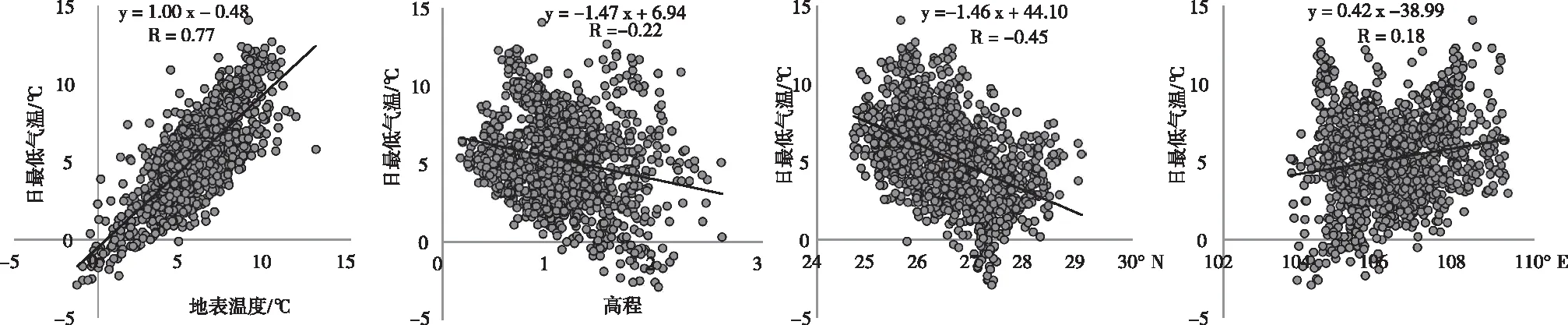
图2 2016年2月10日线性显著通过0.01水平的参数Fig.2 The linearity significantly passed the 0.01 level of the reference substance on February 10, 2016

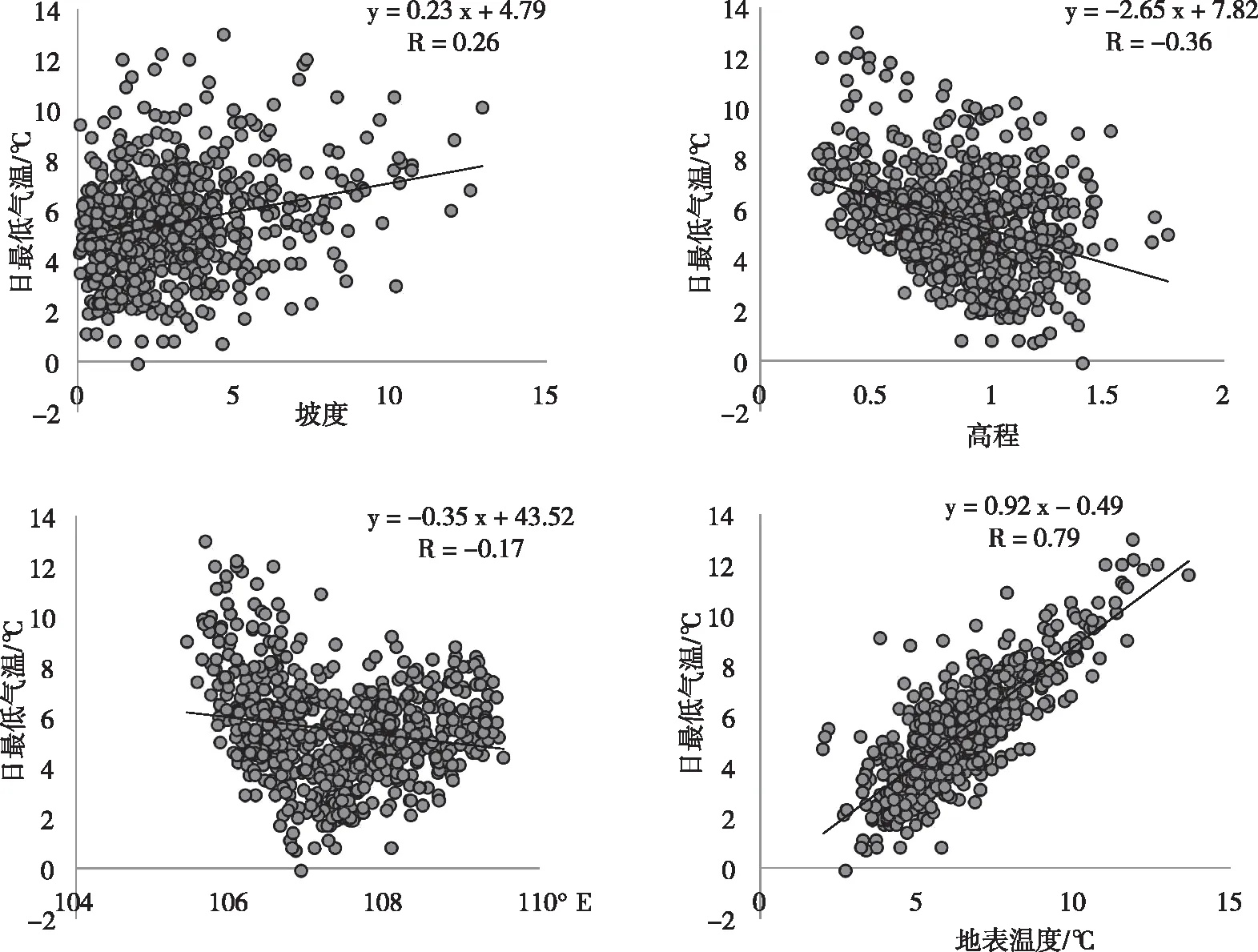
图3 2017年4月1日线性显著性通过0.01水平的参数Fig.3 The linearity significantly passed the 0.01 level of the reference substance on April 1, 2017

图4 2023年1月31日线性显著性通过0.01水平的参数Fig.4 The linearity significantly passed the 0.01 level of the reference substance on January 31, 2023

随机划分2016年2月10日的171个数据作为验证样本,1198个数据作为建模样本;2017年4月1日的99个数据作为验证样本,681个数据作为建模样本;2023年1月31日的188个数据作为验证样本,1866个作为建模样本。验证样本占比10%～13%,建模样本占比87%～90%。根据每个日期得到的显著参数,构建多元线性回归模型:

Y=a1x1+a2x2+…+anxn+b

(1)

式中,Y为日最低气温,x1、x2、…、xn分别为选择的参数,a1、a2、…、an、b为拟合系数。

采用平均绝对误差(MAE)、均方误差(MSE)和均方根误差(RMSE)来评价所建立的推算模型的精度。

3 结果分析

采用多元线性回归方法,利用不同相关性显著的参数,逐步增加建模参数,建立冬季和春季的不同线性回归模型,并用验证样本开展精度评价。

3.1 冬季

冬季的样本有2016年2月10日和2023年1月31日2个时段的数据,建立的不同推算模型及其精度评价见表1和表2。

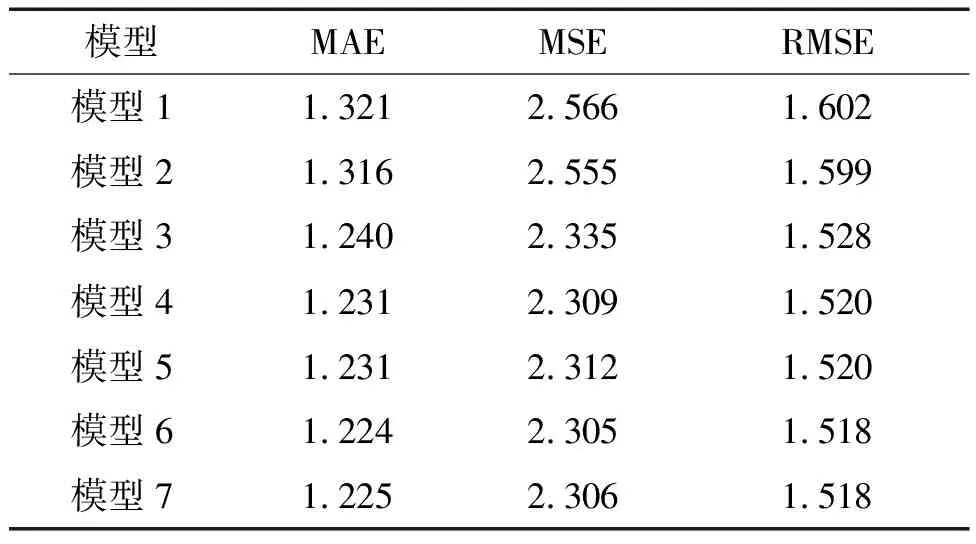
表1 2016年2月10日不同线性模型推算最低气温验证精度对比(单位: ℃)Tab.1 Comparison of verification accuracy of different linear models for calculating minimum temperature on February 10, 2016 (unit:℃)

表1对比结果表明:2016年2月10日的数据,模型6使用地表温度、纬度、经度、高程和水汽5个显著参数建立的线性模型精度最高,相对于只使用地表温度的线性模型,精度有较大提升,其MAE提高了7.3%。

表2对比结果表明:2023年1月31日,使用地表温度和坡度构建的线性模型精度比只使用地表温度的线性模型精度更高一些,但是精度提升不到1%,故此数据只使用地表温度进行日最低气温度推算。

利用2016年2月10日的数据建立多元线性回归模型如下:

y=1.1501x1-0.1228x2+2.6685x3+0.4423x4+0.3330x5-48.7213

(2)

式中,x1、x2、x3、x4、x5分别为地表温度、纬度、高程、经度和水汽变量,变量名前面的数据为拟合的回归系数, -48.7213为常数项。利用2023年1月31日的数据建立一元线性回归模型如下:

y=0.7095x1-1.0104

(3)

式中,x1为地表温度,其中0.7095为拟合的回归系数,-1.0104为常数项。

3.2 春季

冬季使用了2017年4月1日的数据,建立的推算模型及其精度评价见表3。

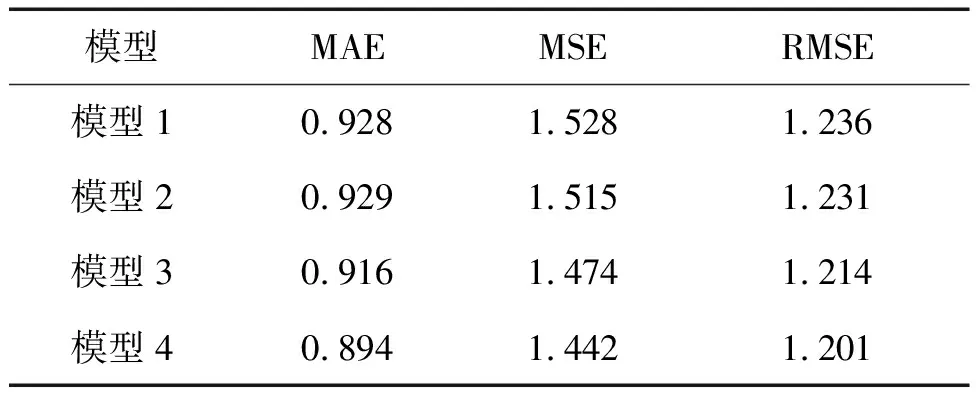
表3 2017年4月1日不同线性模型推算最低气温验证精度对比(单位:℃)Tab.3 Comparison of verification accuracy of different linear models for calculating minimum temperature on April 1, 2017 (unit:℃)

表3对比结果表明:使用地表温度、坡度、高程和经度4个显著参数建立的线性模型精度较高,相对于只使用地表温度的线性模型,精度也有较高提升,其MAE提高了3.7%。

利用2017年4月1日的数据建立多元线性回归模型如下:

y=0.8029x1-1.127x2+0.0749x3-0.2189x4+24.5729

(4)

式中,x1、x2、x3、x4分别为地表温度、高程、坡度和经度变量,变量名前面的数据为拟合的回归系数,24.5729为常数项。

3.3 误差分析

利用模型(2)、(3)和(4),采用经度、纬度、地表温度、水汽含量和高程5种栅格数据,通过ArcGIS的栅格运算功能,分别计算得到全省日最低气温的推算结果(图5～7)。从图5中验证点的平均绝对误差统计结果来看,2016年2月10日平均绝对误差<1 ℃、<2 ℃、<3 ℃的点占比分别为45.0%、81.9%和95.9%,平均绝对误差>3 ℃的点仅占比4.1%。从验证点的平均绝对误差空间分布来看,平均绝对误差>2 ℃的主要分布在中部以南,即日最低气温度较高的区域。从图6中验证点的平均绝对误差分布来看,2017年4月1日平均绝对误差<1 ℃、<2 ℃、<3 ℃的点占比分别为65.7%、87.9%和99.0%,平均绝对误差>3 ℃的点仅占比1%。通过冬季和春季的情况来看,平均绝对误差<2 ℃的验证点均占比超过80%,>3 ℃的点均较少,误差较大的点分布在北部。从图7中验证点的平均绝对误差分布来看,2023年1月31日平均绝对误差<1 ℃、<2 ℃,<3 ℃的点占比分别为33.5%、63.3%、83%,平均绝对误差>3 ℃的点占比17%,误差分布没有明显的区域分布特征。

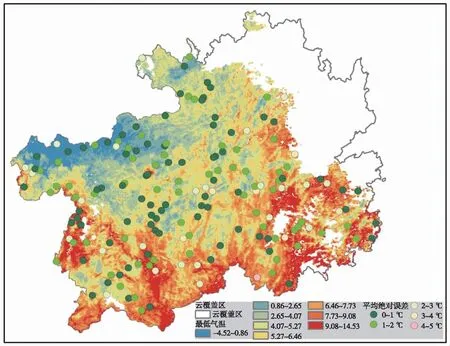
图5 2016年2月10日的日最低气温多元线性模型推算结果及验证点误差空间分布Fig.5 Prediction results and verification point error space distribution of the multivariate linear model for daily minimum temperature on February 10, 2016

图6 2017年4月1日的日最低气温多元线性模型推算结果及验证点误差空间分布Fig.6 Prediction results and verification point error space distribution of the multivariate linear model for daily minimum temperature on April 1,2017

4 结论

通过上文分析,在利用遥感资料进行日最低气温推算的过程中,使用经度、纬度、地表温度、水汽含量和高程5个参数建立日最低气温推算的多元线性回归模型,其平均绝对误差(MAE)均在1 ℃左右,其结果比只使用相关系数最高的地表温度效果有所提高,表明采用夜间地表温度参与的日最低气温推算在冬季和春季能获得较高的精度。

根据线性分析的过程来看,有的参数与日最低气温的线性关系不显著,但是非线性关系较显著,因此可考虑构建复杂的非线性模型,预期可以进一步提高日最低气温的推算结果。

5 讨论分析

为何夜间地表温度和日最低气温的关系如此显著?文献[11]阐明了地表温度和气温之间具有明确的物理关系,但是因为有的参数难以获取导致无法直接反演,因此利用地表温度和实测气温直接建立相关关系成为可行的途径。日最低气温一般出现在凌晨日出前后,夜间地表温度因为没有太阳的辐射能量,主要是地表自身的热辐射,因此比较稳定,而日最低气温出现的时间也受太阳辐射的影响较小,所以夜间地表温度与日最低气温的相关性很高。当然,日最低气温还受到地形和大气状况的影响,所以理论上增加地形和大气状况的参数参与建模能一定程度上提高日最低气温的推算效果。通过与其他研究的对比,本文得到的效果较好,如文献[11]日最低气温的RMSE为2.8～4.1 ℃,这可能与本文使用的站点数量更多有关,也可能因为本文所分析的日期个例较少。

虽然遥感地表温度推算日最低气温的方法具有一定可行性,但由于贵州晴空条件较少,特别是低温冷害时天气多阴雨,更难获得热红外遥感地表温度等地面数据,限制了此方法的应用范围,需继续开发不受天气条件限制的其他推算方法,比如微波反演的地表温度,才能满足全天候条件下的实际业务应用需要。