基于改进Jaccard 系数的柔性直流配电网纵联保护方案

魏 来，李 波，廖 凯，杨健维，何正友

（西南交通大学电气工程学院，四川省成都市 611756）

0 引言

柔性直流配电网具有良好的分布式电源接纳性和较高的供电效率，逐渐成为配电系统的重要发展方向［1-2］。然而，直流配电网故障电流增速快、幅值大，严重威胁系统稳定安全，柔性直流配电网亟需快速、可靠的保护方案［3-4］。

现有直流配电网保护方案主要分为单端量保护和双端量保护两类。其中单端量保护具有速动性优势，但大多依赖限流电抗器等作为保护边界，故应用场景受限且存在保护死区［5-6］。双端量保护从原理上能够保证全线的选择性，也可以更好地适应分布式电源接入带来的拓扑变化［7-8］。随着配电网通信设备配置率和通信技术不断提高［9］，中压配电网线路长度（一般小于10 km）造成的通信延时对保护速动性影响较小，基于双端量的保护方案已具备应用条件。因此，纵联保护成为直流配电网保护的主要发展方向之一［10-11］。

目前直流配电网主要采用频域量和时域量构造纵联保护方案。利用频域分析能够提取更丰富的暂态故障信息，构造合适的判据可提高保护的准确性和适应性。例如，文献［12］利用暂态高频阻抗特征差异构造保护判据，对系统参数变化具有较强的适应性。文献［13］通过在特征频段构造的暂态功率方向判别区内、外故障。但以上方法分别针对极间短路和单极接地故障，多故障类型下的综合保护性能有待验证。文献［14］提出了基于线路直流电抗器两侧电压小波变换细节系数幅值比的方向纵联保护方案，但该方法仅适用于含直流电抗器的配电线路保护。可见，采用频域量构造保护存在算法复杂、依赖高频边界等缺陷，并且直流配电网故障电流在极短时间内有可能未体现周期性特征，难以进行频域分析。

时域量保护数据处理主要利用暂态故障电流、电压等信息特征进行判别。例如，文献［15］利用故障电流过零时刻差别构造保护判据，但方案对信息同步要求较高，且暂态故障电流受干扰后易发生多次过零情况，影响保护性能。文献［16］基于改进动态时间弯曲算法实现两端数据的动态匹配，提高方案的耐同步特性，但行波波头检测难度大，且不适合应用于线路较短的直流配电网。文献［17］采用线路两端的暂态差流作为判别依据，并通过构造两端差流的短时能量，扩大区内、外故障特征差异，但此方法也会放大误差和干扰对数据的影响。文献［18］利用移动数据窗和最小距离方差实现了双端数据自同步，并构建不稳定点剔除判据，提高了双端故障测距方法性能，但注入的扰动信号存在影响系统稳定的风险。采用时域量的保护在数据处理方面简单快速，但数据质量易受影响，导致保护性能受限。

综上所述，直流配电网纵联保护方案主要面临问题为：1）短时间内保护可用数据有限，故障特征难以提取或易受干扰；2）两端信息同步要求较高。现有研究一般通过扩大数据窗长、提高采集频率或采用高复杂度算法，但同时会牺牲保护方案的速动性。

针对上述两个问题，本文提出一种基于改进Jaccard 系数的柔性直流配电网纵联保护方案，从数据预处理和判据构造两方面提高保护耐受同步误差等性能。首先，直流配电网发生区内、区外故障（单极接地及极间短路）时，分析被保护线路两端暂态电流绝对值交集部分特征差异。其次，通过简化的Apollo 曲线光滑算法处理离散电流数据，再利用两端电流绝对值的改进Jaccard 系数构造保护动作判据。最后，基于PSCAD/EMTDC 平台搭建四端环状直流配电网模型，对所提方案在保护可靠性、耐受过渡电阻、抗干扰和耐受同步误差方面进行了仿真验证，结果证明所提纵联保护具有良好的性能。

1 柔性直流配电网暂态故障电流特性分析

直流系统发生故障后数毫秒内，直流侧电容放电导致故障电流迅速上升。为尽量在换流站闭锁前实现故障隔离，本节针对直流侧电容放电阶段的故障电流进行分析。由于直流配电网两极对称运行，选择故障特征分析对象为保护区段两端暂态故障电流绝对值交集部分，以此可忽略电流方向判断和故障选极环节，并为纵联保护动作判据的构造提供理论依据。

1.1 柔性直流配电网系统拓扑结构

本文以图1 所示的典型四端环状柔性直流配电网为例进行分析，额定直流电压为±10 kV，换流站均采用电压源型换流器（VSC），具体参数见附录A表A1、表A2。由于交直流侧接地方式对故障初期（电容放电阶段）的故障特性影响较小，故选择常见的交流侧经联结变压器接地和直流侧经钳位电容接地。

图1 四端环状柔性直流配电网Fig.1 Four-terminal annular flexible DC distribution network

以线路l1作为被保护线路进行分析，分别在f1、f2和f3点设置单极接地故障（正极）和极间短路故障。

1.2 单极接地故障

1.2.1 区内单极接地故障

当f1点发生故障时，线路l1区段正极线路的故障等效电路如图2 所示。

图2 区内单极接地故障等效电路Fig.2 Equivalent circuit of internal pole-to-ground fault

图中：U1、U2分别为故障前区段两端正极直流电压值，I0为故障前区段直流电流值，C1、C2为两端换流站直流侧电容，L1、L2分别为两端到故障点的等效电抗（包括限流电抗和线路电抗），R1、R2分别为两端到故障点的等效电阻，Rf为过渡电阻。定义电流正方向为从母线指向馈线，故保护点1 为正向端，保护点2 为反向端。

故障后电容放电阶段，两端均构成二阶放电回路，故对二阶电路的零输入响应进行求解，可得区段两端故障电流绝对值I1、I2的表达式分别为：

式中：Rf1和Rf2分别为两端故障电流流过的等效过渡电阻；α1、α2分别为正、反向端电流振荡衰减时间常数；ω1、ω2分别为正、反向端振荡放电固有频率。其中，

由式（1）、式（2）可见两端故障电流表达式仅有含I0项符号相反，为进一步分析两端故障电流绝对值数据关系，通过式（1）、式（2）计算1 ms 内两端电流数据，并绘制两端故障电流数据绝对值曲线如图3 所示。

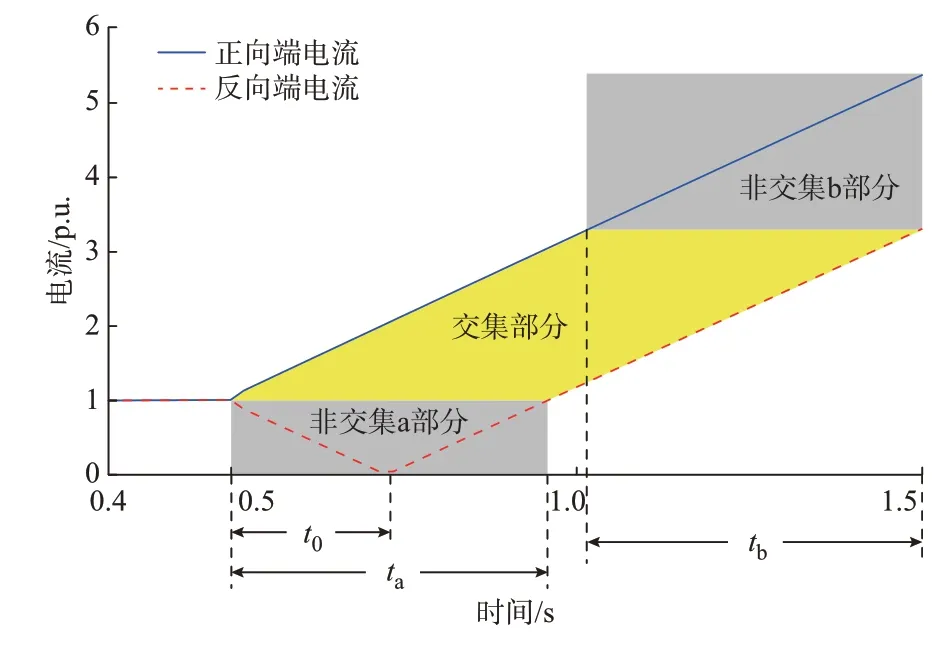
图3 区内单极接地故障两端电流绝对值Fig.3 Absolute value of current at both ends during internal pole-to-ground fault

由图3 可知，故障发生后正、反向端故障电流绝对值存在部分交集，但交集部分难以量化，故对非交集部分进行分析，间接得到两端暂态电流交集部分特征。

非交集部分由两部分组成：1）由于反向端故障电流初始值为负，其绝对值先减小至零后再增大，故存在非交集a 部分；2）由于两端故障电流初值和变化率不同，故障后1 ms 时两端故障电流绝对值不相等，故存在非交集b 部分。

其中，非交集b 部分对应时间与故障位置、数据窗长等因素相关，难以具体量化。非交集a 部分对应的时间与故障电流过零时刻有关，根据式（2）可得t0的计算表达式为：

式中：t0为从故障发生到反向端电流变为零对应的时间段长度。

故障后1 ms 内，故障电流故障变化率仅有极小的衰减。若以故障后瞬间的反向端电流变化率表示故障后1 ms 内的故障电流变化率，则有：

式中：ta为非交集a 部分对应的时间段长度。

当馈线靠近反向端端口处发生金属性单极接地故障时，反向端故障电流变化率较大、正向端电流变化率较小。不考虑线路长度前提下，存在特殊故障位置，使得此情况下非交集b 部分对应时间tb恰好为0。此时非交集部分对应的总时间tfj有最小值，且与非交集a 部分对应时间相同，即tfj最小值tfj，min的表达式为：

式中：ta，min为ta的最小值。

根据以上分析可知，式（5）计算结果为理论最小值。实际故障情况与上述特殊位置重合概率极低，且大多数故障为非金属性故障，非交集部分对应的总时间tfj大于式（5）计算结果。故交集部分对应时间tj最大值tj，max为：

式中：tDW为故障数据采集窗时长。

1.2.2 区外单极接地故障

当f2或f3点发生故障，即正向区外故障或反向区外故障，线路l1区段的故障等效电路见附录A 图A1。由图A1 可知，无论发生正向区外故障还是反向区外故障，保护区段流过穿越性电流，即两端电流绝对值近似一致，以f2点发生故障为例，故障后1 ms内两端电流绝对值见附录A 图A2。

由图A2 可知，保护区段两端故障电流绝对值几乎相等且变化情况一致，因此，两端故障电流绝对值基本全部为交集部分。实际情况中由于正负极运行稍有差异，并受噪声等干扰，两端故障电流绝对值存在差异，但相较于区内故障，发生区外故障时，交集部分仍较大，对应时间tj为：

1.3 极间短路故障

1.3.1 区内极间短路故障

f1点发生极间短路故障时，线路l1区段的故障等效电路见附录A 图A3。当故障位置相同时，单极接地和极间短路故障等效电路形式相似，因此，故障电流绝对值表达式也一致。对比图2 与图A3（b）可知，单极接地和极间短路故障等效电路区别在于：除过渡电阻外的参数为2 倍或1/2 的关系。

由此可知，发生极间短路故障后，正、负极线路的两端故障电流绝对值交集部分特征均与单极接地故障情况相似。并且根据极间短路和单极接地故障等效电路参数关系，推导可知发生区内极间短路故障时，交集部分对应时间最大值tj，max可由式（5）、式（6）求得。

1.3.2 区外极间短路故障

发生区外极间短路故障时，与区内极间短路故障分析过程相同，正、负极线路两端电流绝对值交集部分特征与区外单极接地故障情况一致，即交集部分对应时间tj约为tDW。

综上，发生区内、外极间短路故障时，正、负极线路区段两端电流绝对值交集特征均与单极接地故障情况一致。因此，同一区段的两极线路可独立考虑，发生极间短路故障时可视为两极均发生单极接地故障，故障类型和极性不影响故障特性。

2 纵联保护方案

针对柔性直流配电网中发生区内、外故障时，保护区段两端故障电流绝对值交集部分的差异，本章首先采用简化Apollo 曲线光滑算法对采集的原始电流数据进行预处理，滤除噪声等干扰，提高数据使用效率；其次，利用改进的Jaccard 系数量化区内、外故障电流绝对值交集部分大小，并以此构造保护判据；然后，根据故障电流表达式设置保护判据的整定原则；最后给出所提纵联保护方案的完整流程。

2.1 简化的Apollo 曲线光滑算法

由于短时间内直流配电网保护可用数据的数量和质量有限，需对所采集数据进行预处理，以提取较准确的故障特征。

Apollo 是一种针对离散点的曲线光滑算法。其原理是将原始离散点数据作为参考线，通过对参考线上的离散点进行有限偏移，达到使离散点连线光滑的目的。根据上文分析可知，理想的故障电流波形应为光滑曲线，可采用Apollo 曲线光滑算法对原始数据进行预处理。

Apollo 曲线光滑算法本质上是一个非线性优化模型，目标函数C为：

式中：n为数据点数量；xi、yi为优化后的数据坐标；xi，ref、yi，ref为数据原始 坐标；C1为平滑度代价；C2为长度代价；C3为偏移代价。

约束条件为：

式中：xl和xu分别为X轴正、负移动的最大距离限制；yl和yu分别为Y轴正、负移动的最大距离限制；si为松弛系数；Δs为离散点间平均长度；r为最大曲率约束。

直流配电网对保护速度要求高，需要更高质量数据，故本文基于Apollo 曲线光滑算法原理对数据进行预处理，达到滤除噪声和提高数据质量的效果。但由于Apollo 曲线光滑算法目标函数和约束条件均为非线性方程，求解速度难以满足直流配电网保护速动性要求，因此，对Apollo 曲线光滑算法进行以下简化和改进：

1）离散点仅在Y轴方向进行有限移动；

2）曲率约束主要是考虑车辆转弯半径，本文应用背景下可忽略此约束；

3）分别为3 个代价函数设置权重a1、a2和a3。

简化后的算法目标函数和约束条件分别为：

以故障区段反向端电流数据为例，对简化的Apollo 曲线光滑算法效果进行验证，并选择常用的均值算法进行对比，相关结果见附录A 图A4。

从对比结果可以看出，采用简化Apollo 曲线光滑算法可以有效去除噪声，波形接近理论值，在平滑离散数据的同时也有较好的拟合效果。与均值算法对比发现，均值算法受某些异常点影响较大，易产生较大误差；而简化Apollo 曲线光滑算法维持数据整体变化趋势，并以较光滑的曲线进行拟合，在数据窗中段与理论值的误差更小。同时，均值算法本质上是用几个数据的均值代替此段数据，相当于减少了数据容量。受限于采集频率与精度，直流配电网保护判断可用数据极其有限，采用简化Apollo 曲线光滑算法避免数据容量减少，也不需要对数据点进行重新选取，提高了离散数据使用效率。

但简化Apollo 曲线光滑算法对两端数据的处理较差，效果稍劣于均值算法。因此，在应用时尽量将所需数据置于数据窗中段。

2.2 基于故障电流变化率的保护启动判据

纵联保护在数据处理和通信传输方面压力较大，为避免保护动作判据计算环节频繁启动，利用故障电流变化率设置保护启动判据。然而，采用差分代替微分的常规变化率计算方法精度差，且受噪声等干扰影响明显。故利用一阶导数的五点数值微分算法计算故障电流变化率［19］。保护启动判据ΔI及其整定表达式为：

式中：Δt为数据采集点时间间隔；I′1至I′5为连续5 个采样点数据；δset为保护启动阈值；kset为整定系数。

2.3 基于改进Jaccard 系数的保护动作判据

Jaccard 系数用于比较有限样本集之间的相似性和差异性，集合A与B的Jaccard 系数J（A，B）计算表达式为：

式中：|·|为求集合内元素个数。

故障电流虽然是连续变化的，但采集的电流值为离散数据，量测精度越高，出现相同数据的概率越低，这导致故障和健全区段两端故障电流数据的绝对值均难以出现交集。因此，需要对故障电流数据进一步处理，并对Jaccard 系数的计算进行改进。

1）电流数据分段化

为避免区段两端故障电流数据的绝对值出现无交集情况，需设置分段梯度，将连续的电流范围分段化，离散的电流数据即可归算至对应的分段范围。但只有对电流数据设置合适的段间距，Jaccard 系数才能反映数据特性：若梯度过小，仍会存在无交集情况；若梯度过大，分段数过少，则会导致区内、外故障时，Jaccard 系数均接近1。

由1.2 节可知，所观测数据窗内的故障电流变化率逐渐减小且变化范围较小，故根据初始故障电流的变化率设置分段梯度值。若将保护启动判据数据值作为保护动作判据的起始数据，则初始故障电流的变化率即为保护启动判据值，从而避免重复计算，提高计算速度。再取区段两端的故障电流变化率平均值，得到分段梯度值Δi为：

式中：ΔIZ和ΔIF分别为正向端和反向端的启动判据值。

利用式（14）计算结果对数据进行分段，可以使数据尽量分布在连续且不同的分段中，有利于后续Jaccard 系数计算。

2）考虑集合元素频度

Jaccard 系数求交集时不考虑元素出现的频度，即多个相同元素不重复计算。而通过图3 可知，特别是故障区段的反向端，存在部分重合数据；图A2中数据整体变化范围较小，分段化后集合元素较少。因此，在计算两端故障电流绝对值的Jaccard 系数时考虑元素出现频度，扩大区内、外故障特性差异，充分利用全数据特征。

通过以上步骤，将正、反向端故障电流绝对值分别对应为集合A、B，通过计算Jaccard 系数可量化正、反向端故障电流绝对值相似度，即交集部分对应时间tj的大小，从而判别区内、外故障，保护动作判据J的表达式为：

式 中：NA、NB分 别 为 集 合A、B的 元 素 个 数；NAB为A、B交集的元素个数；Jset为保护动作阈值。

根据1.2 节、1.3 节分析结果可知，区段两端故障电流绝对值的交集部分对应总时间最大值tj，max可通过式（6）计算。因此，可以得到保护动作阈值Jset的整定表达式：

式中：kJ为裕度参数，目的是提高保护判据性能。

2.4 故障选极与隔离方案

根据1.2 节、1.3 节分析可知，发生单极接地或极间短路故障时，同一区段的两极线路可独立考虑，即以单极线路为保护对象，故在发生不同类型故障时，均不需要故障选极环节。当保护识别为区内单极接地故障时，故障极线路两端断路器动作，并向同侧对应区段断路器发送动作指令；极间短路故障时，两极线路断路器接收的动作指令相互独立。若需服务于后续故障定位及故障恢复，可根据断路器接收的动作指令差异区分故障所在线路极性。

2.5 保护方案流程

基于改进Jaccard 系数直流配电网纵联保护方案的完整流程如图4 所示。

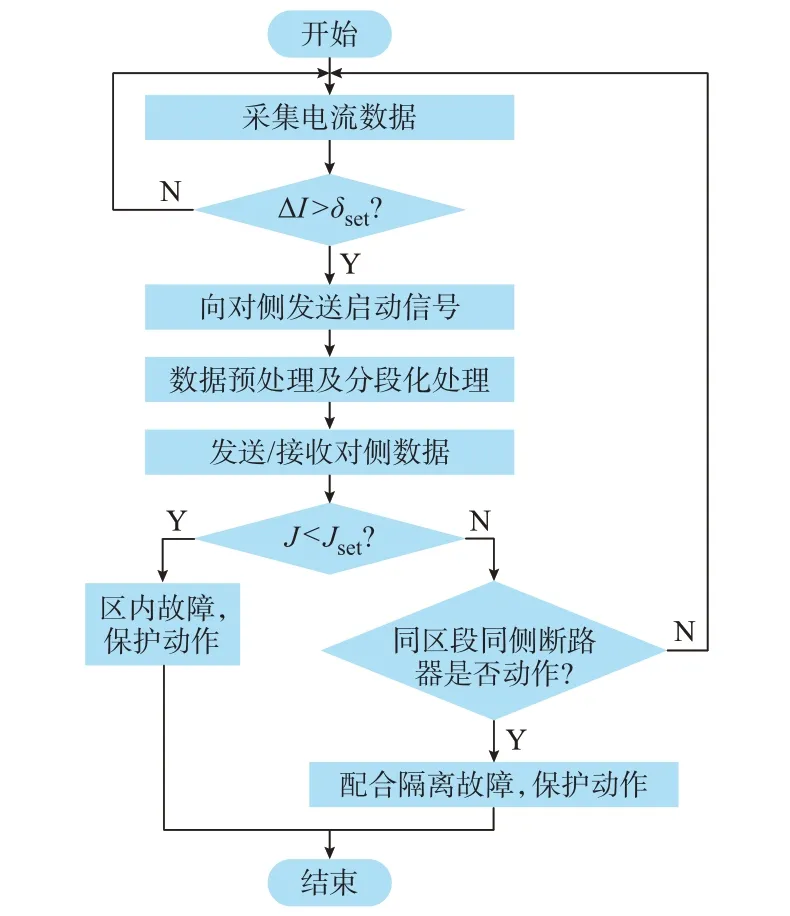
图4 纵联保护方案流程图Fig.4 Flow chart of pilot protection scheme

1）首先，当保护单元计算采集的电流数据满足式（12），本侧保护启动，并向对侧发送启动信号；

2）其次，两端保护单元分别以启动判据数据为起始点，通过简化的Apollo 曲线光滑算法，对1 ms内的电流数据进行预处理，并将处理后的数据发送至对侧；

3）然后，计算两端电流数据的改进Jaccard 系数J，若满足式（15），则本侧保护动作，并向对侧发送动作信号；

4）若未满足式（15），而同区段同侧断路器动作，则该断路器为配合故障隔离，仍需进行动作。反之，保护不动作。

3 仿真验证

为验证所提基于改进Jaccard 系数直流配电网纵联保护方案的有效性，利用PSCAD/EMTDC 平台，搭建了如图1 所示的四端±10 kV 中压直流配电网模型，负荷1、负荷2 分别为2 MW、3 MW，换流站参数和线路参数见附录A 表A1、表A2。设置故障时刻为0.5 s，数据采样频率为50 kHz，数据窗长设置为1 ms。根据以上参数，本文设置保护启动判据整定值为100 A/ms，通过式（16）计算，设置保护动作判据Jset为0.75。

3.1 区内、外故障验证

1）单极接地故障

以线路l1为观测对象，当f1点发生单极接地故障时，两端保护启动判据值分别为881.3 A/ms 和877.8 A/ms，明显超出启动判据阈值，纵联保护启动。通过Apollo 曲线光滑算法进行数据预处理后，根据式（14）计算得到正、反向端电流数据分段的梯度值约为18 A。再通过式（15）计算线路l1区段的保护动作判据值J1为0.66，小于Jset，故区段两端的保护单元均动作。

以上过程中，输出窗长1 ms，数据预处理时间约为1 ms，动作启动和动作判据计算时间均不超过0.1 ms，光纤通信延迟约为4.9 μs/km［20］，故考虑保护算法用时和通信耗时，直流断路器在故障后约2.25 ms 内收到动作信号，满足保护速动性要求。

为验证所提纵联保护方案的全线保护能力，改变f1点到馈线正向端出口的距离d，线路l1区段的保护启动和动作判据值如图5 所示。

由图5 可知，改变故障点位置后，保护启动判据均明显大于整定值，且正、反向端随故障点位置变化规律相反。由于保护动作判据整定考虑了最特殊的故障点位置情况，本文所提纵联保护方案受故障点位置影响极小，保护均能够可靠启动，实现区段全长保护。

当f2点发生故障时，对线路l1区段为正向区外故障；当f3点发生故障时，对线路l1区段为反向区外故障。分别在两点处设置单极接地故障，并改变故障点与正向端距离d，线路l1区段的保护情况如表1所示。

表1 不同故障位置下的保护动作情况Table 1 Protection operations at different fault locations

由表1 结果可知，发生区外故障时，区段两端电流数据的Jaccard 系数均为1，即全部为交集部分，与1.2.2 节理论分析结果一致。与区内故障仿真结果对比，判据值差异明显。因此，所提方案能够可靠识别区内、外故障。

2）极间短路故障

以线路l1为观测对象，依次在f1、f2和f3点设置极间短路故障，并与其他故障条件相同的单极（正极）接地故障情况进行对比，保护启动和保护动作判据值如表2 所示。

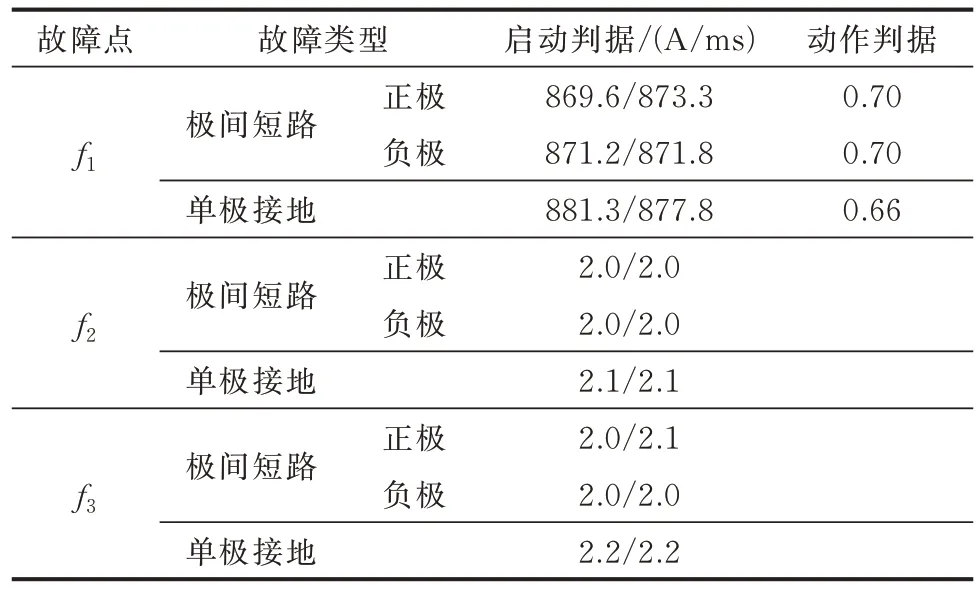
表2 极间短路故障与单极接地故障判据对比情况Table 2 Comparison of criteria for pole-to-pole shortcircuit faults and pole-to-ground faults

由表2 可知，发生区内极间短路故障时，启动判据值与同条件下的单极接地故障启动判据值接近，保护能够可靠启动；动作判据值略大于单极接地故障动作判据值，但小于整定值Jset，保护仍能够可靠动作。发生区外极间短路故障时，启动判据值远小于100 A/ms，故保护能够避免不必要的动作判据计算和误动。

此外，针对极间短路故障的计算和分析均将正、负极线路独立考虑，由表2 结果可知，极间短路与相同故障情况下的单极接地故障保护动作情况相同。因此，所提保护方案不需要增加故障选极环节，有利于保护速动性提升。

3）不同拓扑结构

为验证所提方案在其他拓扑结构中的适用性，参考文献［21-22］搭建双端“手拉手”和七端环网柔性直流配电网，具体拓扑结构如附录A 图A5、图A6所示，仿真结果如附录A 表A3、表A4 所示。由仿真结果可知，所提保护方案均能够准确识别区内、外故障并可靠动作。此外，由四端环状和七端环状结构下的仿真结果可进一步类推出所提方案能够适用于其他多端环状柔性直流配电网。

3.2 过渡电阻耐受能力验证

直流配电网中大多数故障为非金属性故障。因此，需要验证所提保护方案在不同过渡电阻下的性能。以f1点发生单极接地故障为例，依次设置过渡电阻为1、10、20、30 Ω，对应的两端故障电流的绝对值如附录A 图A7 所示。由图A7 可知，随着过渡电阻增大，保护区段两端电流绝对值的变化率均随时间逐渐减小，交集部分也随之减小，即动作判据值减小，保护更能够可靠动作。根据式（2）至式（6），当过渡电阻增大时，非交集a、b 部分均增大，故交集部分减小，图A7 的仿真结果与理论推导一致。

当过渡电阻大于20 Ω 时，两端电流绝对值无交集部分，此时动作判据值为0，远远小于保护动作阈值。综上可知，保护动作判据的性能随过渡电阻增大而提高。因此，需要确定所提保护方案启动判据适用范围，此范围内，动作判据均有极高的耐受过渡电阻能力。

以过渡电阻梯度为20 Ω 设置多组故障情况，并改变f1点位置。由于现有数据采样条件对启动判据计算结果的影响，故考虑1%的测量误差［23］。由3.1节分析可知，正、反向端随故障点位置变化规律相反，故对一端启动判据分析即可。单极接地故障的正向端启动判据，以及极间短路故障正极线路的正向端启动判据如附录A 图A8、图A9 所示。由图A8、图A9 可知，启动判据值随过渡电阻增大而减小，单极接地故障时至少可以耐受100 Ω 的过渡电阻，极间短路故障时至少可以耐受200 Ω 的过渡电阻。结合1.2 节、1.3 节分析，当极间短路故障的过渡电阻约为其余条件相同的单极接地故障过渡电阻2 倍时，则故障电流表达式完全一致，即故障电流增长率相同。因此，极间短路故障的启动判据耐受过渡电阻值约为单极接地故障情况下的2 倍。

此外，本文所搭建模型中线路l1正常运行时电流约为150 A，保护启动判据为100 A/ms。当测量误差为1%时，不会导致保护启动，避免了保护动作判据频繁计算。

3.3 抗噪声干扰能力验证

由于直流配电网故障发展迅速，且选择的数据采集频率较高，噪声干扰对保护判据影响明显。因此，为充分验证所提保护方案的性能，分别在f1和f2点发生0.01 Ω 单极接地故障后的电流数据中，加入20 dB 以上的高斯白噪声［24］，计算得到线路l1区段的保护动作情况如表3 所示。

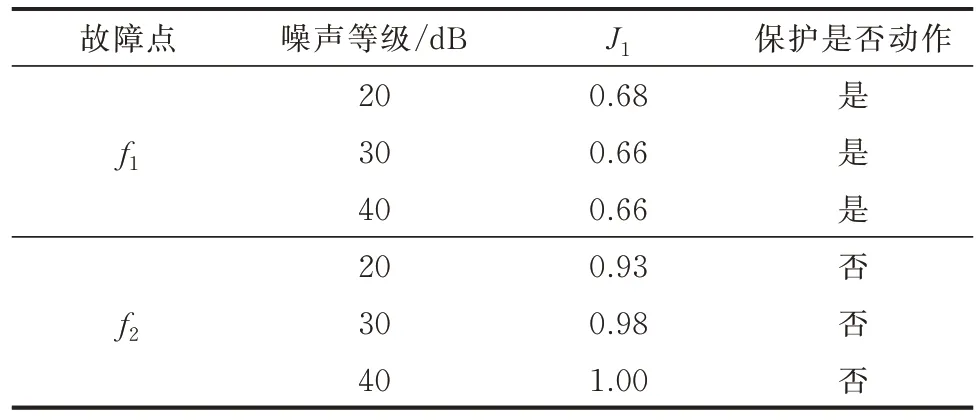
表3 不同噪声等级下的保护动作情况Table 3 Protection operations at different noise levels

对比表3 中区内、区外故障保护判据值随信噪比的变化情况，可以看出噪声对区外故障的判据值变化影响更明显，原因是区外故障电流变化率小，噪声导致的数据波动对其变化率的计算结果影响明显，进而影响分段值的选取，最终影响判据值。而区内故障电流变化率明显，噪声造成的数据波动相较于电流整体变化范围较小，对保护判据值的影响也较小。

从保护动作情况可知，本文所提保护方案无误动或拒动情况，具有较好的抗干扰能力。并且在不同信噪比情况下，保护判据相对稳定，证明所采用的简化Apollo 曲线光滑算法对数据的预处理效果明显，有效降低了噪声对保护判据计算的影响，提高了保护的可靠性。

3.4 同步误差耐受能力验证

对于保护速动性要求较高的直流配电网，信息同步对纵联保护的影响更加明显。因此，耐同步误差能力对于直流配电网保护十分重要。同步误差主要存在两种情况。

1）同时刻数据不对应

由所构造保护动作判据的原理分析可知，本文将两端故障电流绝对值数据各作为一个集合，再计算两集合的改进Jaccard 系数，故不需要各数据一一对应，保证数据窗起始点误差在合理范围内即可，起始点误差范围要求见下文分析。

2）起始对时存在误差

数据窗起始对时误差将影响保护判据值，以f1点发生金属性单极接地故障为例进行分析，两端数据存在起始对时误差的情况如图6 所示。

图6 数据存在起始对时误差仿真结果Fig.6 Simulation results of data with initial timing error

当正向端延迟于反向端时，从图6（a）中可知，两端故障电流绝对值交集部分减小，即动作判据变小，有利于保护动作。当反向端延迟于正向端时，从图6（b）中可知，交集部分增大，动作判据变大，保护易拒动，需进一步进行分析。

故障位置变化对故障电流绝对值变化率的影响不同，故不同故障位置情况下，相同对时误差对交集部分的影响不同，进而影响保护判据。故障位置对交集部分的具体影响如附录A 图A10 所示。由图A10 可知，假设对时误差为n个数据点，当故障发生在正向端端口时，即图A10（a），由于正向端故障电流变化率大于反向端，故交集部分增加数据点个数小于2n；同理，当故障发生在线路中点时，即图A10（b），交集部分增加数据点个数等于2n；故障点继续向反向端靠近时，交集部分增加数据点个数大于2n。不考虑线路长度时，当两端故障电流关系如图A10（c）所示时，交集部分增加数据点数量最多，即保护判据最大。因此，若线路足够长，图A10（c）对应情况下保护最易发生拒动；若线路长度有限，则反向端端口处最易发生拒动。

附录A 图A10（d）为1.2.1 节中所分析的极特殊情况，即保护判据的整定依据。与图A10（c）相比，图A10（d）对应的故障位置更靠近反向端，而保护判据在整定时考虑一定裕量，减少了部分对时误差影响。当对时误差为0.5 ms 时，保护动作情况如表4 所示。

表4 对时误差为0.5 ms 时的保护动作情况Table 4 Protection operations with 0.5 ms timing error

由表4 可知，对时误差为0.5 ms 时保护仍能正确动作，因此起始点误差要求不大于0.5 ms。而目前全球定位系统（GPS）和北斗对时误差最小可保证在2 μs 以内［23］，故耐受对时误差的能力满足要求。

综上，同时刻数据不对应和起始对时误差对保护动作判据的影响均较小，所提保护方案的整体耐同步误差能力较强。

3.5 数据采样频率影响分析

现有直流电网数据采样频率大多为10 kHz 或20 kHz，张北直流工程采用的互感器采样频率为100 kHz［25］，上文分析与验证的采样频率为50 kHz，符合现有技术条件。由于Jaccard 系数属于统计类指标，故集合元素数量越大，Jaccard 系数体现的数据特征越准确。因此，不同采样频率对应的保护性能也存在差异，需分析所提保护适用的采样频率范围。对同一故障情况分别取采样频率为10、20、50、100 kHz，保护判据的计算结果如表5 所示。

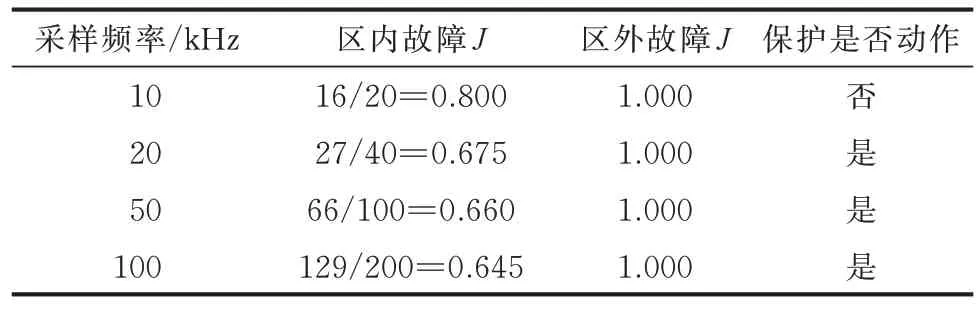
表5 不同采样频率下的判据值Table 5 Criterion values at different sampling frequencies

由表5 可知，发生区外故障时，保护方案性能不受影响；发生区内故障时，所提保护方案可适用于20 kHz 以上的采样频率。

采样频率影响所提保护判据的主要原因是：1）采集频率越高，集合元素数量越多，保护判据值的精度不同；2）根据1.2 节的分析，非重叠部分a 的大小与反向端故障电流过零点有关，而故障后电流增长速度快，以本文所搭建模型为例，过渡电阻较小时，故障后约0.2 ms 内反向端电流即会过零。故当采集频率小于20 kHz 时，前5 个点有可能不全在过零点同侧，导致电流变化率计算结果偏小，进而影响保护启动判据和动作判据。

因此，对本文所提方法，选择50 kHz 采样频率时，既可避免电流变化率计算误差过大，也能够保证两端电流数据集合有合适数量的元素，提高保护可靠性。

3.6 数据窗选取的影响分析

由于数据窗的选取会影响所提保护判据计算，需对数据窗长、数据窗位置对保护的影响进行分析，具体分析结果如附录A 表A5、图A11 所示。根据仿真结果可知，所提方案所适用的数据窗长应不大于1.5 ms，且当故障发生后数据窗延迟4 ms 情况下保护仍能正常启动并动作，证明所提方案受数据窗位置影响较小。

此外，由3.1 节、3.2 节中故障位置和过渡电阻对保护影响的仿真分析结果可知，在满足数据窗长和位置的要求下，所提方案能够实现全线保护，并具有较高的耐受过渡电阻能力。此外，由于线路参数同样是通过改变故障初期的放电回路参数，进而影响两端故障电流特性。因此，上述3 种因素对数据窗选取影响较小。

附录A 图A12 为不同换流器参数下数据窗内的故障电流波形。通过仿真对比可知，直流侧电容变化仅改变故障电流值，但不影响电流故障特性变化趋势，保护动作判据相近。故换流器参数对数据窗选取影响也较小。

3.7 与其他保护方案的对比分析

为进一步分析所提方案各方面性能和原理特点，选择其他直流配电网电流方向保护［2，15］和基于电流相关性的保护方案［10，26］进行对比。

1）保护性能

为降低故障特性选择和数据分析角度对保护方案特点的影响，选择其他两种利用两端电流方向故障特征的直流配电网纵联保护方案进行对比分析：基于直流电流过零特征的保护［15］和基于拟合电流斜率特性的保护［2］。

附录A 表A6 为3 种方案的保护范围、动作时间、抗噪声干扰能力和耐受同步误差能力对比结果。可知，3 种保护方案均能实现全线保护和准确的故障识别。与其他两种保护方案对比，本文所提方案的动作时间较短，且受故障类型等因素影响较小，在抗噪声干扰和耐受同步误差能力方面也较强，保护可靠性较高。

2）原理特点

选择其他两种基于两端电流相关性的直流纵联保护方案进行对比。一种是利用波形结构的余弦相似度算法［26］，cosθ计算表达式如下：

式 中：{X1，X2，…，Xn}和{Y1，Y2，…，Yn}为 线 路 两端的电流采样值序列。

另一种是利用数据相关系数的t检验算法［10］，系数t计算表达式如下：

分别采用3 种算法对同一段数据进行多次重复计算，平均运算时间分别为：Jaccard 系数0.04 ms，余弦相似度0.05 ms，t检验算法0.07 ms。故数据量相同情况下Jaccard 系数运算时间相对较少。

此外，余弦相似度易受到异常值影响，该方案未给出具体判据整定方法，实际使用时比较依赖仿真结果；t检验算法是假设检验的一种，首先要计算检验统计量，再通过检验统计量的临界值表确定概率值P，临界值选择不当会影响保护性能。

相比之下，本文所提算法的判据整定考虑极端故障情况，并设置了裕度系数，推导出与系统元件和运行参数相关的判据整定表达式，可根据不同的系统模型进行整定，不依赖仿真结果，具有较好的适用性。

4 结语

本文针对现有直流配电网保护方案的数据利用率较低、数据同步要求高的问题，提出了一种基于改进Jaccard 系数的柔性直流配电网纵联保护方案，通过理论分析和仿真验证得出以下结论：

1）故障和健全区段两端电流绝对值的交集部分存在差异，通过计算两端电流绝对值的改进Jaccard系数可以进行区分，且不需要方向元件和故障选极环节，但仍具备故障选极能力。

2）本文所提保护方案流程简单，采用简化的Apollo 曲线光滑算法对数据进行预处理，提高了数据利用率，所提保护动作判据能够准确识别区内、外故障，可靠性较高。

3）仿真验证结果表明，所提保护方案具有较高的耐受过渡电阻和抗噪声干扰能力，并至少能够耐受0.5 ms 的同步误差。同时，所提保护方案最低可适用20 kHz 采样频率。

本文所提方案的数据预处理时间占保护流程总时间的比例较大，且构造保护判据所适用的最优采样频率较高，工程应用成本大。下一步将在数据采集和通信要求方面对方案进行改进，并进一步研究基于该方法的双端故障定位方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。