基于钻孔伪标签半监督深度学习的沈阳市浅表地层三维建模研究
2023-12-09徐学闯,张恒兵,符韶华,刘升传,王徐磊,郭甲腾*,敦力民
徐 学 闯,张 恒 兵,符 韶 华,刘 升 传,王 徐 磊,郭 甲 腾*,敦 力 民
(1.东北大学资源与土木工程学院,辽宁 沈阳 110004;2.沈阳市勘察测绘研究院有限公司,辽宁 沈阳 110004)
0 引言
智慧城市[1]已成为当前我国城市建设的重要目标,为合理安排城市地表和地下工程建设,需要通过详细的岩土工程勘察对城市各区域地下资源展开综合评估。地质空间分布具有复杂性、模糊性与不确定性,三维地质建模[2-5]能直观表达地质特征,展示地质构造的空间形态,揭示地质现象的空间分布规律。钻孔数据是三维地质建模最常用的数据[6],基于钻孔数据的三维地质建模可分为显式建模和隐式曲面建模两大类[7,8]:①显式三维地质建模方法包括广义三棱柱(GTP)方法[9]、多层DEM建模方法[10]、剖面建模方法[11]、参数化建模方法[12]等,在建模时更易加入地质语义约束,边界控制较准确,更适用于局部区域的精细建模,但应用于城市大范围建模时,存在建模自动化程度低、模型难以动态更新问题。②隐式曲面三维地质建模方法[13-17]包括克里格法[18]、反距离加权法[19]、径向基函数法[20]等,通过选取适当的基函数,利用空间已知点解算空间曲面的隐式方程,得到隐式曲面函数,最后提取等值面进行显式化网格表达。该类方法自动化程度高,建立的模型易于更新,且表面更光滑,但隐式曲面形态与选取的基函数密切相关,对于地质构造的最终表达存在函数依赖,难以评估未采样区域,模型存在不确定性。
近年来,机器学习在地质建模领域逐步得到应用,如通过训练神经网络从地震数据中预测地质构造[21],利用深度神经网络反演复杂二元地质介质[22]并通过生成对抗网络构建地质模型[23];应用深度学习综合利用钻孔、地质、重力、航磁数据智能生成区域三维地质模型[24,25],或基于二维垂直剖面和现场调查数据采用IC-XGBoost3D方法构建三维地质模型[26],基于钻孔文本数据对岩性进行分类[27],并进行三维地质建模[28]等,但基于钻孔空间与地层数据及地貌单元约束的深度学习建模研究仍较少。
基于钻孔空间数据的机器学习建模主要分为钻孔序列模拟和钻孔空间点模拟两种思路:前者包括钻孔层序预测及各地层厚度预测[29],过程较复杂,但在垂直方向上连续性更好;后者对钻孔采样的空间点进行岩性模拟,准确率更高[30],但需对钻孔按照一定间隔升采样,并以每个采样点作为输入数据[31]。常用的升采样方法主要有:基于少量钻孔数据通过支持向量机预测栅格单元,从而建立三维地质模型[32];基于少量钻孔数据随机选取B样条曲线函数生成地层,并将每个地层的体素采样作为输入[33],构建的地层模型更准确;将每个地层的钻孔坐标和起始深度作为输入[34],模型精度相比升采样有所降低,但通过提取地形特征可防止出现地层顺序颠覆情况。综上,基于钻孔数据的建模方法中,对空间点进行岩性预测的方法效果更好,但针对大规模、多地层、分布不均匀的钻孔数据如何建立准确率较高的三维地质模型仍缺少研究。鉴于此,本文提出一种基于钻孔伪标签深度学习的建模方法,基于沈阳市三环内1.2万条钻孔数据建模,并将建模结果与隐式曲面方法建模结果相比较,根据地貌单元对建模结果与地层的符合程度验证方法的有效性。
1 研究方法
本文采用深度学习方法进行三维地质建模,可将建模问题进一步简化为地层的分类问题。其中,钻孔的坐标数据和地层深度数据作为输入向量,钻孔的地层属性作为输出向量。实现流程(图1)为:首先,通过升采样方法将连续一维的原始钻孔数据离散化,得到标签数据,并将预测空间栅格化,得到待预测的网格点;其次,设计基于高置信度伪标签的半监督深度学习模型,利用标签数据训练模型,再用训练好的模型对无标签的钻孔数据进行预测,并为无标签数据添加置信度高的伪标签数据,扩大样本数据量;最后,采用标签数据和伪标签数据训练模型,得到分类模型,加入地貌单元约束后得到三维地质模型。

图1 基于大规模钻孔数据的伪标签半监督深度学习城市三维地质建模流程Fig.1 Flowchart for urban 3D geological modeling using semi-supervised deep learning with pseudo-labels based on a large amount of borehole data
1.1 钻孔数据预处理
钻孔数据主要包括钻孔坐标(X、Y)、钻孔标高、地层厚度、地层层底深度、钻孔标号、钻孔地层标号等。由于原始钻孔数据为连续一维数据,并且钻孔数据不同数据项的位数长度差距较大,不能直接用于神经网络的训练,需对钻孔数据进行预处理。
1.1.1 钻孔数据升采样 为增加数据量,需要对钻孔数据进行升采样处理。钻孔各个地层之间的厚度可能相差较多,地层较厚的数据量会显著大于地层较薄的数据量,如果采用等间隔采样,数据的平衡性会受到影响,训练网络时地层较厚的采样数据将占据主导地位,导致在对未知区域地层进行分类和预测时,易将未知区域的地层属性预测为与较厚地层一致,且地层厚度相差越大,误分类概率越高。非等间隔采样(图2a)可根据不同地层的厚度改变采样间隔,从而保证采样数据的平衡性,因此,本文采用非等间隔采样方法。如图2所示,地层数据以条带状显示,在垂直方向上连续分布,单个地层的深度区间地层属性连续唯一,且地层与地层之间没有数据空隙,第i个钻孔第j层的采样间隔Hi,j计算公式为:
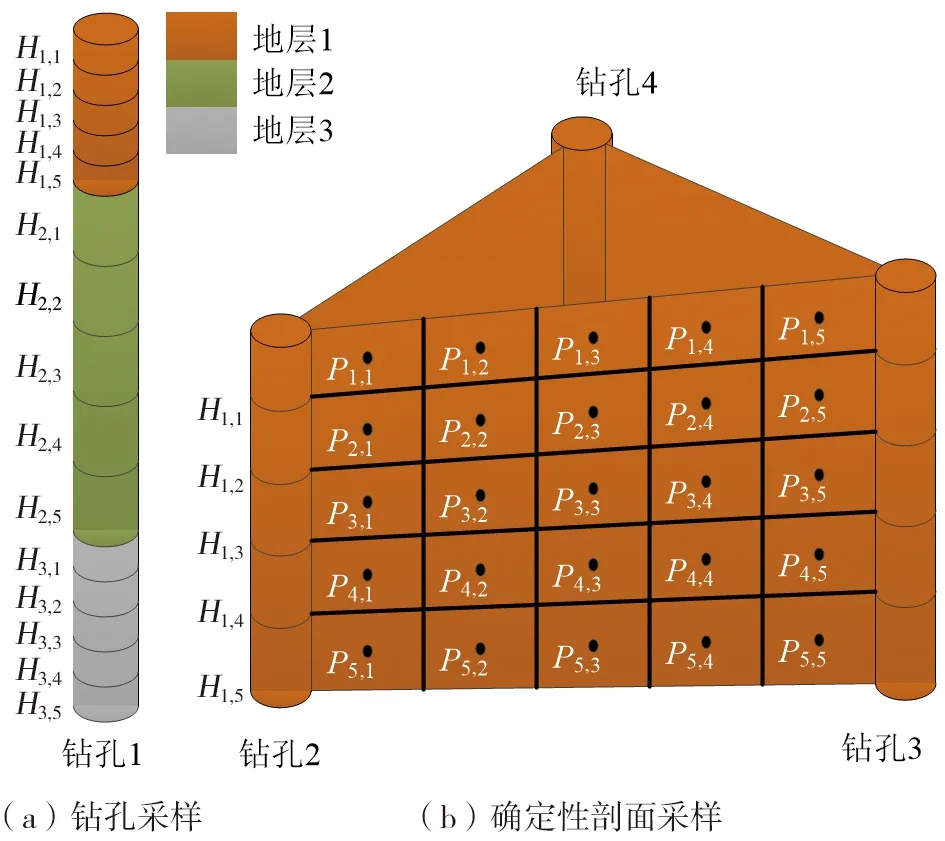
图2 钻孔及确定性剖面非等间隔采样原理Fig.2 Unequally spaced sampling principle of boreholes and deterministic sections
Hi,j=(di,j-di,j-1)/n
(1)
式中:di,j为第i个钻孔第j层地层的层底深度,n为每个地层的采样数量。
1.1.2 确定性剖面升采样 将钻孔点依据Delaunay法生成不规则三角网(TIN)[35],确立钻孔间的基本拓扑关系,每个三角网包含的3个相邻钻孔中,若两两钻孔之间地层属性相同,则连接为一个确定性剖面,这种类似广义三棱柱模型(GTP)[9]的剖面连接方法能保持3个钻孔之间的内部联系,可以模拟多种结构较复杂的地质现象;之后对确定性剖面在水平方向和垂直方向进行非等间隔采样(图2b),采样密度与钻孔密度一致,避免采样过密影响网络训练。此外,为消除关联性较低、相距较远钻孔连接对地层预测的错误影响,在TIN中剔除狭长三角形。针对确定性剖面的非等间隔采样点坐标公式为:
(2)
式中:Pi,j,x、Pi,j,y、Pi,j,z分别为剖面上第i行第j列采样点的x、y、z坐标,(x1,y1)、(x2,y2)分别为剖面连接的两个钻孔坐标,A1、B1、C1、D1、A2、B2、C2、D2分别为连接剖面钻孔在该地层的地层顶端连线和地层底端连线的直线方程参数,n为采样数量。
1.1.3 预测空间栅格化 根据钻孔的分布建立凸包确定建模范围,模型顶面采用钻孔孔口构建的TIN网约束,模型底面根据钻孔孔底建立的凸包确定。考虑钻孔深度不一致,采用基底填充模型底部,基底底面深度与钻孔最大深度相同。依据确立的建模范围和建模精度计算网格点位置,即三维地质建模时待预测地层属性的点位。
1.1.4 钻孔数据归一化 钻孔数据中坐标数据(一般为7~8位整数,3位小数)与地层深度(一般为1~2位整数,1位小数)等数据的位数长度差距较大,容易导致参数难以训练,最终影响模型的训练结果。为消除输入特征之间的位数影响,使不同特征对模型的训练具有相同的影响力,保证收敛,需对数据进行最大最小值归一化处理,将结果值映射到0~1之间。通过归一化方法,网络的优化器在更新梯度时不易产生震荡,训练模型的收敛速度和训练准确率更高,建立的三维地质模型连续性更好。
1.2 基于伪标签方法的半监督深度学习
1.2.1 人工神经网络构建 多层感知机(MLP)[36]通过对输入指标和输出指标进行训练学习形成某种规则,在输入指标后给出最接近期望输出值的结果,是按照误差反向传播算法的多层前馈神经网络。该网络模型以预测区域中每个升采样空间点坐标数据(x,y,z)作为输入,以空间点的地层属性作为输出。输入数据经过多层隐含层后输出,与期望标签相比较后得到对应的误差,误差通过反向传播算法对应调整每一层的权重,最后可得到适合该模型的权重。隐含层神经元的数量根据模型复杂程度变化,隐含层之间用RELU作为激活函数。为防止网络过拟合,在网络倒数第二层和倒数第三层的全连接层增加Dropout函数,随机减少神经元,然后,通过一层全连接层和Softmax层将类别的输出值经过指数函数变化后归一化为各类别的概率(和为1),最后,将每个数据点预测的结果整合,形成整个三维地质模型(图3)。网络模型优化器使用Adam优化器,损失函数采用多分类任务中常用的交叉熵损失函数L(式(3))。
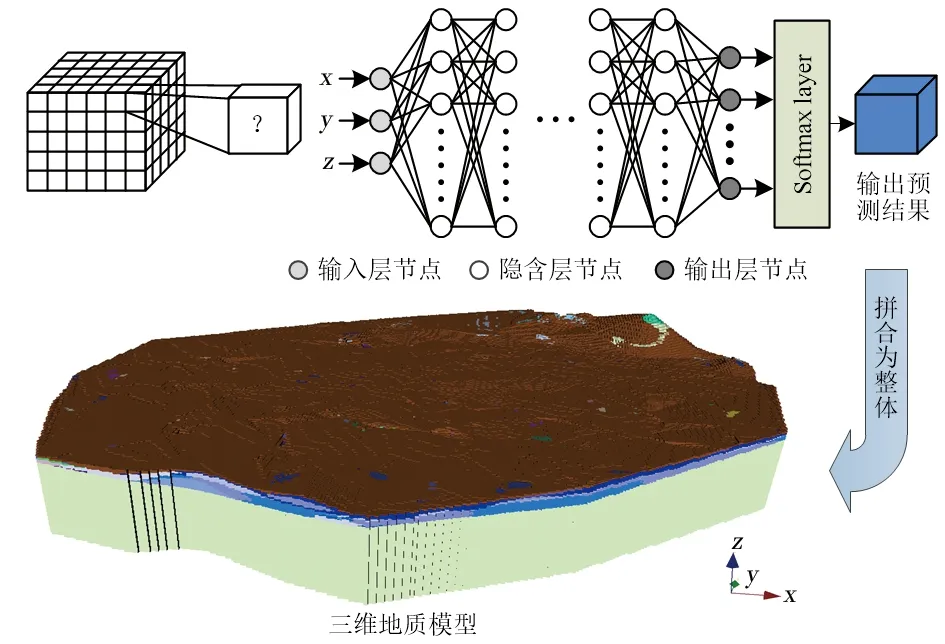
图3 人工神经网络建立三维地质模型流程Fig.3 Process of 3D geological modeling using artificial neural network
L=Lsup+αLsemi
(3)
式中:Lsup为有标签样本训练的损失函数,Lsemi为伪标签样本训练的损失函数,α为用于调节监督损失和半监督损失之间的学习权重。
1.2.2 高置信度伪标签添加 相比图像、点云等数据,钻孔数据的空间分布具有局部集中、整体分散的群簇状特点,难以准确表达整个地层分界面的倾向、倾角等变化特征。深度学习需要大量的标签数据提升模型性能,仅依据有限的钻孔点数据、确定性钻孔剖面的升采样数据,对于城市大范围建模精度要求较高的海量空间栅格点而言,标签数据量非常少,包含的特征十分有限。为有效解决数据量问题,为无标签数据添加伪标签,有利于扩大样本空间。首先通过标签数据对模型训练到较高准确率后,采用训练好的模型预测数据,筛选出预测结果置信度较高的数据作为伪标签;将伪标签数据和标签数据结合再进行模型训练,训练一定轮次后,重复上述过程,直至每轮新增的伪标签数据低于一定比例,此时认为大多数数据已经获得置信度较高的标签,模型已对全部数据进行充分训练。
1.3 地貌单元约束
地貌单元和地层之间存在着重要关系,地层反映了地质体的构造,而地貌单元反映了地质体的形态,将二者结合可以更好地发掘和分析地质体的三维空间分布特征。为避免某些地层延展到不应出现的地貌单元内,对模型预测结果添加边界约束(式(4),表示各网格点地层属性的最终预测结果应是当前地貌单元中预测概率最大的地层)以限制地层的预测范围,使预测结果更符合地质语义。
S={j|Fj=max(F0,F1,…,Fn),j∈Ui}
(4)
式中:S为预测地层,Fn为所有地层预测概率,Ui为地貌单元i涵盖的地层属性。
2 三维地质建模验证与分析
基于沈阳市三环内的1.2万条钻孔数据,使用本文方法开展三维地质建模与分析实验,并与监督深度学习方法[34](只采用标签数据对人工神经网络进行训练)的训练准确率和HRBF隐式曲面方法[8]的建模效果进行对比。测试的硬件环境为:Intel(R) Core(TM) i7-10750H CPU @2.60 GHz,NVIDIA GeForce RTX 2060,16.0 GB RAM,Windows10(64位)。将所有采样数据按照3∶1∶1划分为训练集、验证集、测试集。神经网络采用8层的隐层结构,第一层隐含层神经元数量设置为16个,并随深度成倍增加,使用RELU函数作为激活函数,初始学习率设为0.003,训练的batchsize设置为4 096,损失函数中α取0.1。在训练过程中,采用学习率衰减策略,训练700周期后首次衰减,之后每100周期衰减一次,学习率衰减率为0.8。模型训练准确率达到800个epoch后,每100个epoch对无标签数据标记一次伪标签,当新增的伪标签数据低于本次判断的无标签数据的10%后,模型继续训练至总计2 500个epoch后停止训练。
2.1 研究区概况
沈阳市区以平原为主,山地、丘陵集中在东北部,其老地貌不断被破坏改造,新地貌不断形成[37],沈阳市三环范围内共有低漫滩、冲洪积高漫滩、浑河冲洪积一级阶地、浑河冲洪积二级阶地、波状岗台地、剥蚀丘陵6种地貌单元[38],地势由东北向西南倾斜,有4条大型河流穿过。本实验共获得研究区域12 419条岩土工程勘察钻孔数据,涵盖56种地层,钻孔分布在25 725 m × 22 706 m的区域内,钻孔平均深度98 m,钻孔揭示地层的最小厚度为0.01 m,呈群簇状或条带状分布(图4)。

图4 钻孔数据在各地貌单元的分布情况Fig.4 Distribution of borehole data in each geomorphic unit
2.2 模型训练准确率和损失对比
由图5可知,本文方法在训练集和验证集上的准确率和损失变化曲线基本一致,说明模型训练质量较好,没有出现明显的过拟合现象;当标签数据和伪标签数据融合训练时,准确率达93.3%以上且损失函数趋于收敛。监督深度学习方法采用相同的网络结构、初始参数和学习率衰减方法,模型训练准确率达82.3%以上且损失函数趋于收敛(图6)。可以看出,本文方法准确率更高。

图5 基于钻孔数据的伪标签半监督深度学习模型训练准确率和损失变化Fig.5 Training accuracy and loss variation curves of semi-supervised deep learning with pseudo-labels based on borehole data

图6 基于钻孔数据的监督深度学习模型训练准确率和损失变化Fig.6 Training accuracy and loss variation curves of supervised deep learning based on borehole data
2.3 建模效果对比
为进一步验证模型精度,将本文方法所建模型与HRBF隐式曲面方法所建模型进行对比,模型的最小栅格单元为100 m × 88 m × 0.88 m。本文方法采用钻孔孔口三角网约束顶面,钻孔孔底凸包约束底面,根据采样点对地层进行分类,隐式曲面方法采用DEM数据约束顶面,底面深度为固定深度,采用控制点约束各地层延展范围,两种模型建模结果分别在Z轴方向上拉伸20倍,以便观察,且为便于对比,将隐式曲面方法建立的三维地质矢量模型转换为栅格模型。
由图7可知,由于本文方法根据钻孔孔底约束凸包基底,而隐式曲面方法根据曲面控制点约束基底,模型边界钻孔较浅,因此,两种方法所建模型在边界下缘有差异;两种方法所建模型的总体地层走向较接近,基本能在钻孔附近正确预测地层倾向、倾角,揭示地层的覆盖关系。此外,钻孔分布是否均匀、建模精度高低均会影响模型地层层序的正确率,在水平方向上以建模精度为间隔,对所建模型进行地层层序比较,最终得到模型地层层序的正确率为83.03%,可见正确率较高。
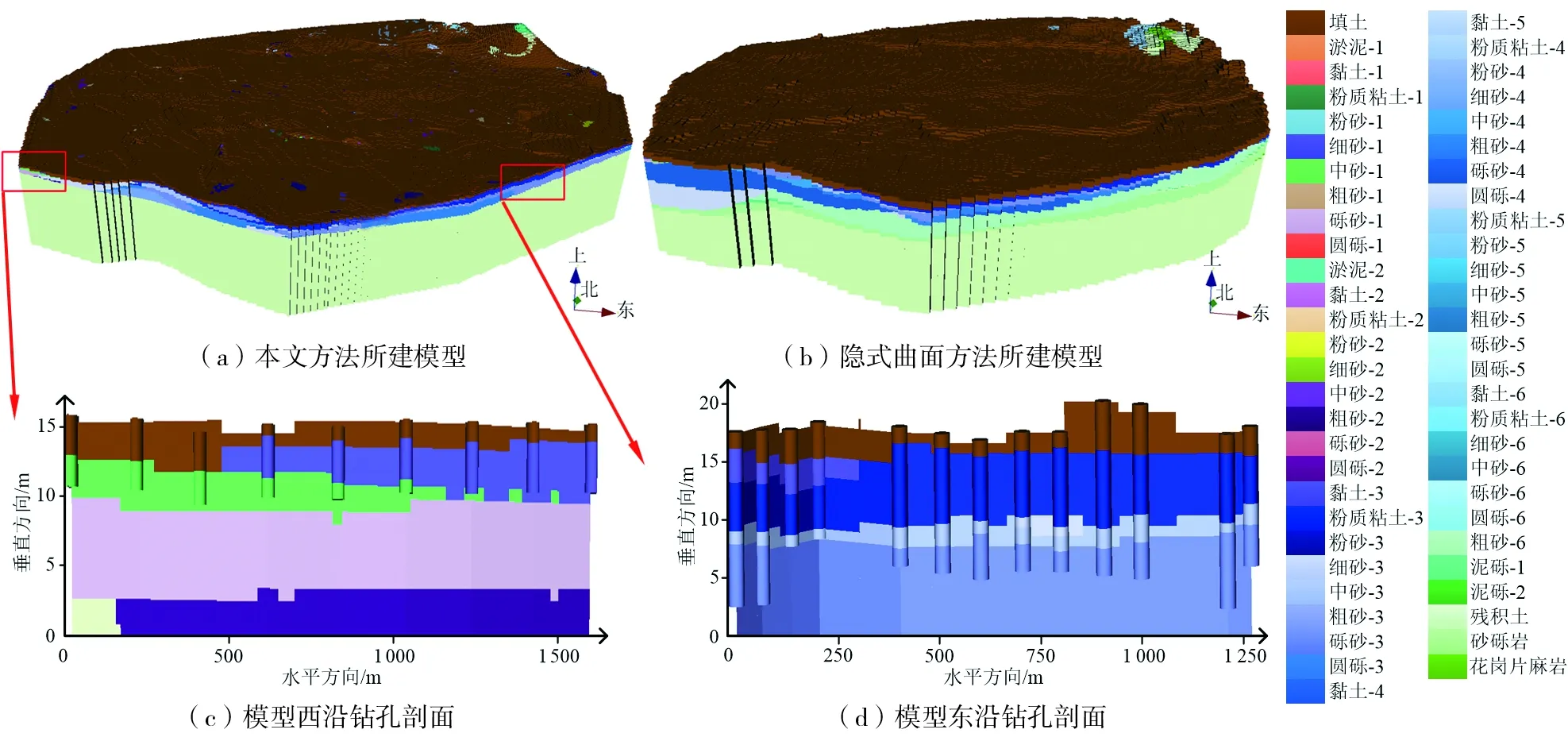
图7 沈阳市三维地质模型Fig.7 3D geological model of Shenyang City
从研究区选取3条剖线(图8),对本文方法所建三维地质模型分别进行沿远距离钻孔剖切和沿连续钻孔剖切(图9),可以看出,钻孔处地层和剖面地层较一致,地层在钻孔之间基本符合地层覆盖关系;由于缺少数据约束,钻孔下地层大多符合覆盖关系,在跨越地貌单元处,剖面地层受钻孔分布约束(图9a);本文方法所建三维地质模型的地层厚度和倾角变化与钻孔所揭示的内容符合度高,符合地质语义。

图8 沈阳市三维地质模型与地貌单元的关系Fig.8 Relationship between the 3D geological model and geomorphic units of Shenyang City
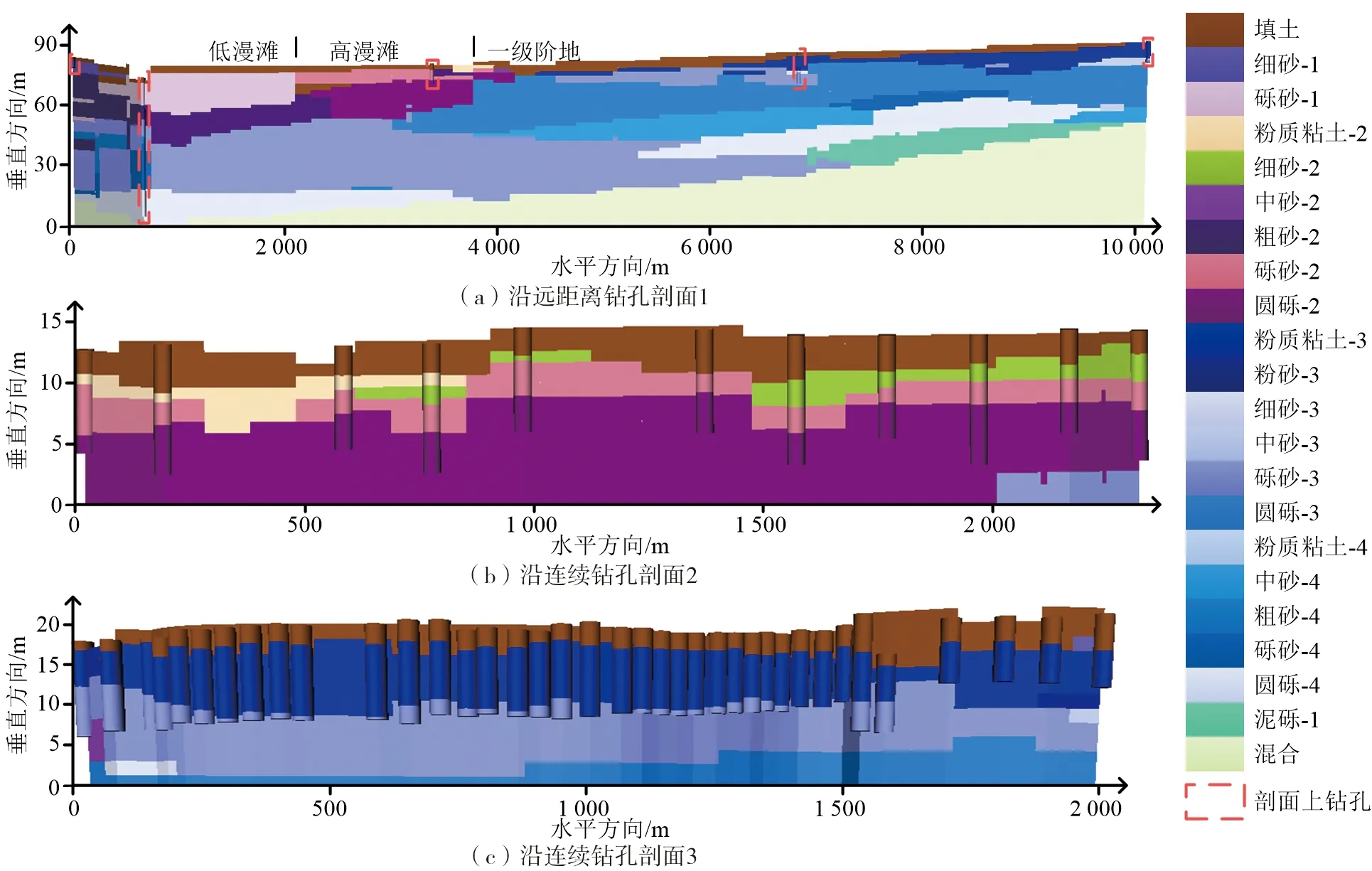
图9 本文方法构建的沈阳市三维地质模型沿钻孔剖面Fig.9 Sections along the boreholes for the 3D geological model of Shenyang City constructed by the proposed method in this paper
由图10可知,在各地貌单元中,两种方法构建的模型较接近,在部分钻孔数据相距较远或线性排列的情况下,本文方法在各地貌单元中基本能在接近的位置预测出和隐式曲面方法相近的地层属性,表明本文方法预测能力较好。
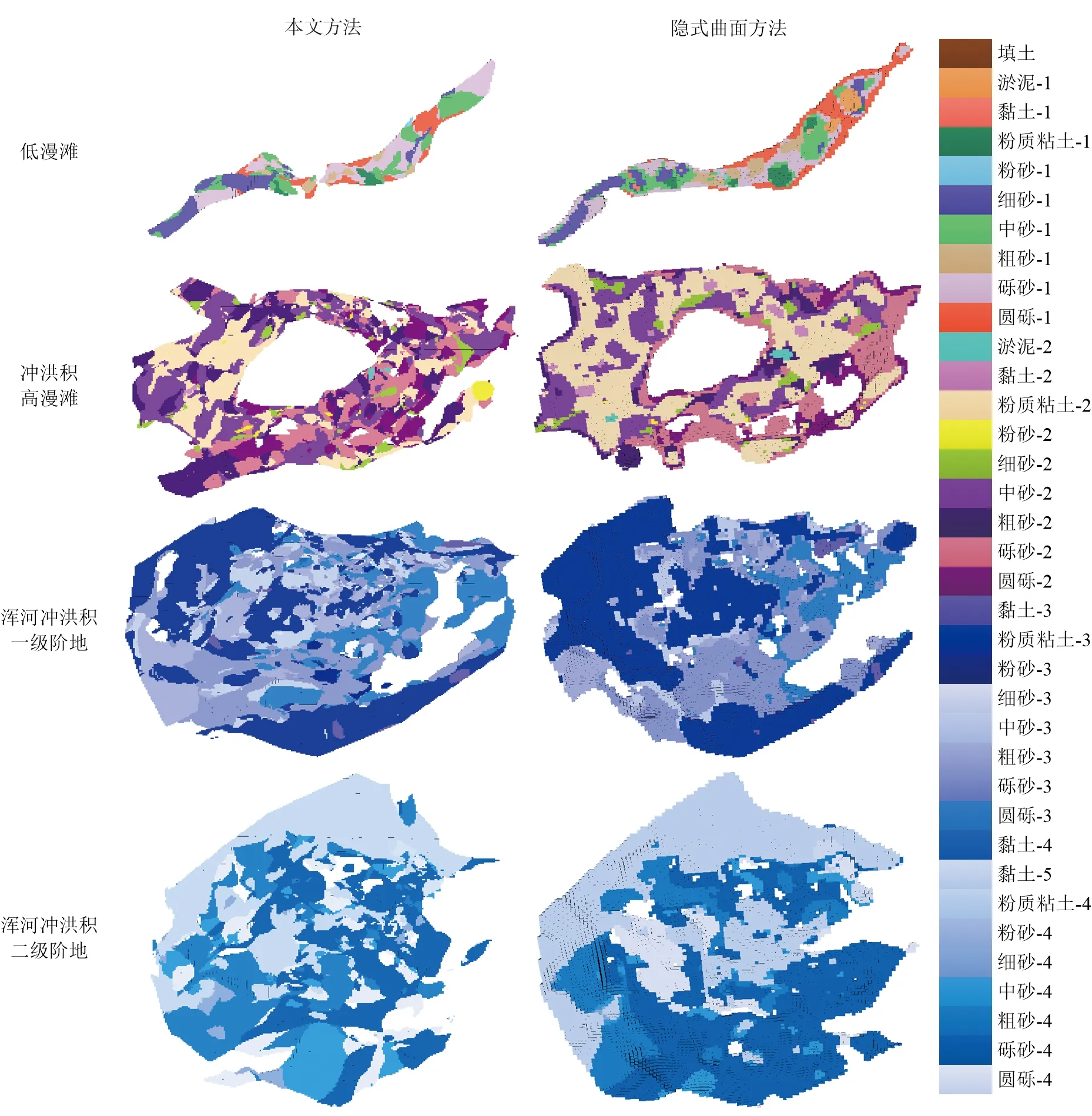
图10 沈阳市三维地层模型空间分布Fig.10 Spatial distribution of the 3D stratum model of Shenyang City
对两种方法所建模型不同地貌单元内各地层占比进行比较(图11),发现两种方法建模结果中各地层占比均较接近,进一步表明本文方法所建模型的正确性与合理性。
3 结论
本文针对城市三维地质建模问题,提出一种基于平原城市大规模浅层钻孔数据的伪标签半监督学习自动建模方法,并依据沈阳市涵盖56类地层的1.2万余条岩土工程勘察钻孔数据建立沈阳市三维地质模型。研究结果表明:①通过对钻孔数据进行预处理得到标签数据和无标签数据,采用伪标签半监督学习方法进行训练,结合地貌单元对模型进行约束,可以解决大规模、多地层、分布不均匀钻孔数据的高精度深度学习三维地质建模问题;②通过对待预测网格点添加高置信度伪标签,可大量扩展训练数据,与监督深度学习方法相比,提高了模型训练的准确率,即提高了三维地质模型与钻孔的符合度;③通过在模型预测时添加地貌单元约束,预测的三维地质模型地层分布更符合地质语义。
由于钻孔数据空间分布稀疏、不均匀,本文选择的非等间隔采样方法解决了数据严重不平衡导致的地层缺失问题,但导致部分钻孔采样信息损失,如何获取更好的重构钻孔数据仍需进一步研究。此外,隐式曲面方法建立的为栅格化后的模型,存在模型精度问题,而本文方法受钻孔地层数量分布影响更大,部分地层的预测统计结果会受影响,有待进一步研究。
