基于π定理及多元线性回归的河道稳定水力几何形态公式研究

闫志方,贾云飞

(1.广东珠荣工程设计有限公司,广东 广州 510610;2.广州开发区财政投资建设项目管理中心,广东 广州 510000)

河道水力几何形态指河道流量、输沙率、河宽、水深、流速等之间的相互关系,稳定水力几何形态即在挟沙水流长期作用下可能形成的与所在河段流量、泥沙等条件相适应某种均衡形态[1]。准确预测一定水沙条件下河道断面的稳定水力几何形态对河道防洪、渠道设计、河道整治、航运码头建设等均有重要意义。河道稳定水力几何形态最早是由Kennedy[2]开展研究,经过大量地汇总分析印度渠道的不冲不淤资料,构建了平均水深H与平均流速U之间的经验关系。继Kennedy后,大量学者开始了对稳定特征变量经验关系的研究:Lindley[3]认为稳定河道的形态取决于流量、床沙的天然特性和床沙的输沙量以及河段的粗糙度,他对Chenab运河下游展开了广泛勘察并收集了观测数据,最终得到了稳定河道中稳定河宽、稳定水深、稳定比降、稳定流速之间的经验关系式;Lacy[4-5]分析了大量可用数据并提出了3个方程,阻力方程、河宽方程、比降方程,其中河宽方程和比降方程分别建立了稳定河宽、稳定比降和造床流量的经验关系;Leopold等[6]针对美国中西部的河流建立了稳定河道方程,他们通过观察发现对河流的稳定特征参量可用同一频率下流量的指数形式表示;Blench[7]应用2个分别代表河床材料和河岸材料参数,并且又引入了一个阻力方程,联立后得出了稳定河宽、稳定水深、稳定比降与造床流量之间的显式方程;钱海强[8]根据西北江三角洲多年实测数据,采用Leopold的水力几何形态关系建立了北江三水河段断面河相关系并探讨了其河相特征及其变化;李倩[9]通过对国内404个实测河道断面数据进行分析,提出了一套以流域面积和河流发育系数为标准的河流宽度计算方法。以上经验方法得到的稳定水力几何形态关系式看似简单,但是其重要性是不可估量的,这些经验方程为渠道、河道、航运等设计提供了有效的工具,在实践中被广泛应用。

然而,利用以上方法得到的结果,存在很大区域局限性,一般也只适用于资料来源区,前人的方法也是针对资料来源区所拟合的经验公式。与前人得到的河道稳定水力几何形态经验关系式不同的是,本文基于π定理找出了影响参数,运用大量原型观测和水槽实验资料作为样本数据进行线性回归分析,提出了稳定河道水力几何形态关系式。

1 量纲分析

本文所研究的河道水力几何形态特征参数主要有稳定河宽、稳定水深、造床流量、床沙中值粒径等。Yalin等[10]提出与河道稳定水力几何形态相关的变量AR可用Q、ρ、υ、γs、D、g表示:

AR=fA(Q,ρ,υ,γs,D,g)

(1)

则稳定河宽和稳定水深可以表示为:

BR=fB(Q,ρ,υ,γs,D,g)

(2)

hR=fh(Q,ρ,υ,γs,D,g)

(3)

式中AR——河道稳定水力几何形态变量;BR——稳定河宽,m;hR——稳定水深,m;Q——造床流量,m3/s;ρ——水流密度,kg/m3;υ——水流运动黏滞系数,m2/s;γs——床沙容重,kN/m3;D——床沙粒径,本文中为中值粒径,mm;g ——重力加速度,m/s2。

分别选取D、Q、γs为几何学、运动学、动力学量,且3个量相互独立。

应用π定理:

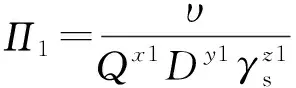
(4)

(5)

(6)

式(4)—(6)分子和分母应满足量纲一致性,则第一个因子的量纲关系有:

[υ]=[Q]x1[D]y1[γs]z1

(7)

即 [L2T-1]=[L3T-1]x1[L]y1[ML-2T-2]z1

(8)

由式子两边量纲相等,得到:

[L]:2=3x1+y1-2z2

[T]:-1=-x1-2z2

[M]:0=-z2

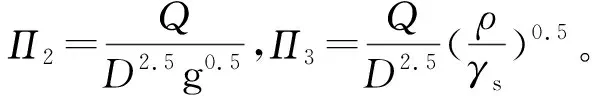
则式(2)、(3)可变为:

(9)

(10)

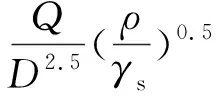
(11)

(12)

2 公式拟合

2.1 样本数据来源

本文样本数据来源于前人发表文献及工程报告[11-23],数据主要涉及加拿大安大略省西南部诸河流、加拿大阿尔伯塔省诸河流、美墨边境格兰德河等河流。为使拟合公式更适用于天然冲积河流,本文从从原始数据中选取宽深比50.05 mm。其中包括11组原型观测数据及2组实验数据,见表1。

2.2 数据分析

a)lnΠ1

从图1看出,ln(BR/D)与lnΠ1、lnΠ2有较明显的线性关系,且根据lnΠ1和lnΠ2的不同取值,ln(BR/D)～lnΠ1和ln(BR/D)～ lnΠ2显现不同的线性关系,其关系分为3部分,其中lnΠ2<16及lnΠ2>18.5两部分样本点相关性显著,R2分别为0.887和0.961,在两部分的过渡区域16≤lnΠ2≤18.5,ln(BR/D)与lnΠ2之间相关性不明显;ln(BR/D)～lnΠ1的关系同样分为3部分,其中lnΠ2<16及lnΠ2>18.5两部分样本点相关性显著,R2分别为0.827和0.958,同样在两段的过渡区域16≤lnΠ2≤18.5,ln(BR/D)与lnΠ1关系不明确。

同样从图2看出,ln(hR/D)与lnΠ1、lnΠ2有较明显的线性关系,且根据lnΠ1和lnΠ2的不同取值,ln(hR/D)～lnΠ1和ln(hR/D)～ lnΠ2分别有不同的线性关系,其相关关系分为3部分,其中lnΠ2<16及lnΠ2>18.5两部分样本点相关性显著,R2分别为0.865和0.932,在两部分的过渡区域16≤lnΠ2≤18.5,ln(hR/D)与lnΠ2之间相关性不明显;ln(hR/D)～lnΠ1的关系同样分为3部分,其中lnΠ2<16及lnΠ2>18.5两部分样本点相关性显著,R2分别为0.442和0.775,同样在两段的过渡区域16≤lnΠ2≤18.5,ln(hR/D)与lnΠ1关系不明确,R2仅为0.009。

图1、2这种分段分布的特性与以往一些学者研究的到经验公式法是不同的,并且通过这些规律本文作者进行猜想,图中的过渡区域可能是天然冲积河流某种特征发生转变的过渡状态。

2.3 公式拟合

通过上文对样本数据分析,可在线性相关显著的区域(lnΠ2<16及lnΠ2>18.5)分别建立以ln(BR/D)、ln(hR/D)为因变量,lnΠ1和lnΠ2为自变量的二元线性回归方程(13)和(14):

(13)

(14)

式中,aB、bB、cB、ah、bh、ch分别为待定参数,Π1、Π2含义同式(9)、(10)。

通过二元线型回归分析求得式(13)、(14)的待定参数及相关性见表2、3。

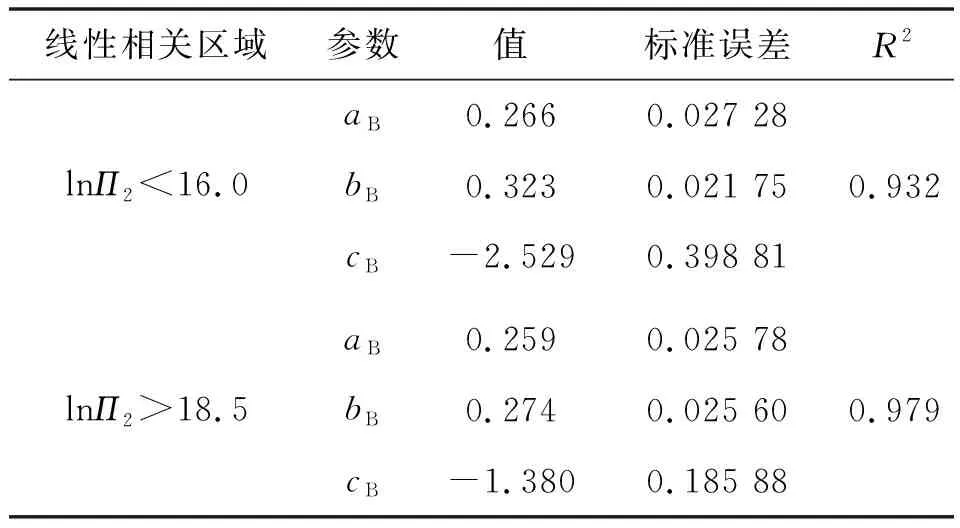
表2 式(13)待定参数值、标准误差及R2

表3 式(14)待定参数值、标准误差及R2

将表2、3中各参数代入式(13)、(14),分别得出式(15)、(16)。

(15)

(16)

分别将式(15)、(16)去对数得式(17)、(18)。

(17)

(18)

式中各符号含义见式(1)—(3)。

从式(15)—(18)看出,本文得到的关系式在16≤lnΠ2≤18.5区间关系混乱,没有较好的表达式,这也不难联想到雷诺数与阻力系数的关系与之类似,因此针对本文提出的经验方法还有待深入研究,以得到具有普遍适用性的河道稳定水力几何形态计算方法。

3 公式精度检验

3.1 检验数据

本文用于公式精度检验的数据来源于文献[24-28],主要涉及河流为土库曼斯坦Kara-Kum河、俄罗斯Saratov河、新西兰Porter河、中国长江等河流,并且检验数据与用于公式拟合的样本数据不同源(表4)。

表4 检验数据来源及变化范围

3.2 公式检验

戴文鸿等[29]通过对3种经典的稳定河道水力几何形态计算方法进行了分析与比选,选出了计算精度较高的Yalin和da Silva方法。故本文将采用Yalin和da Silva方法作为标准方法,分别将式(17)、(18)及Yalin和da Silva方法计算出的稳定水力几何形态,以实测值为横坐标,计算值为纵坐标,对计算结果进行对比,结果见图3、4。

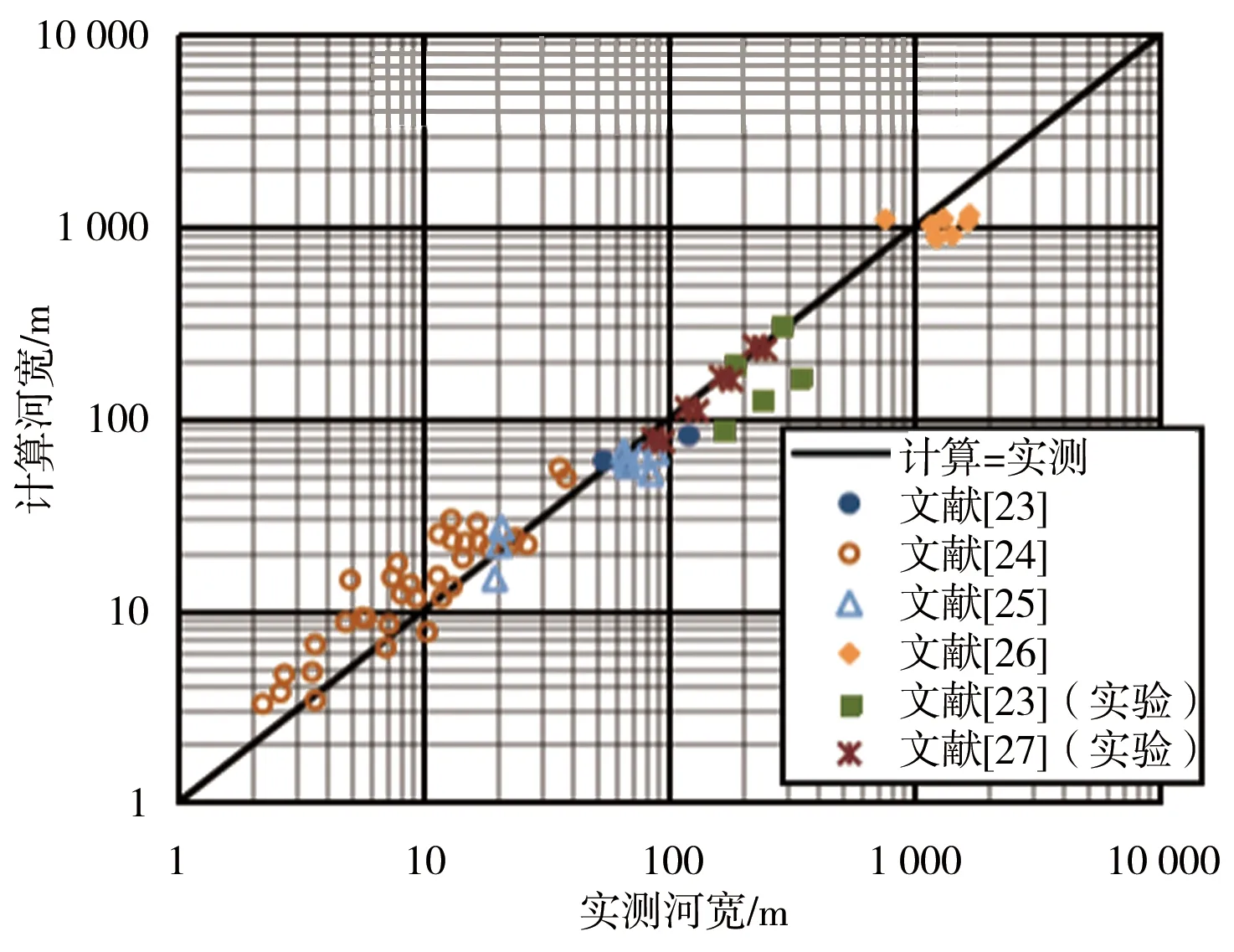
a)式(17)、(18)计算结果

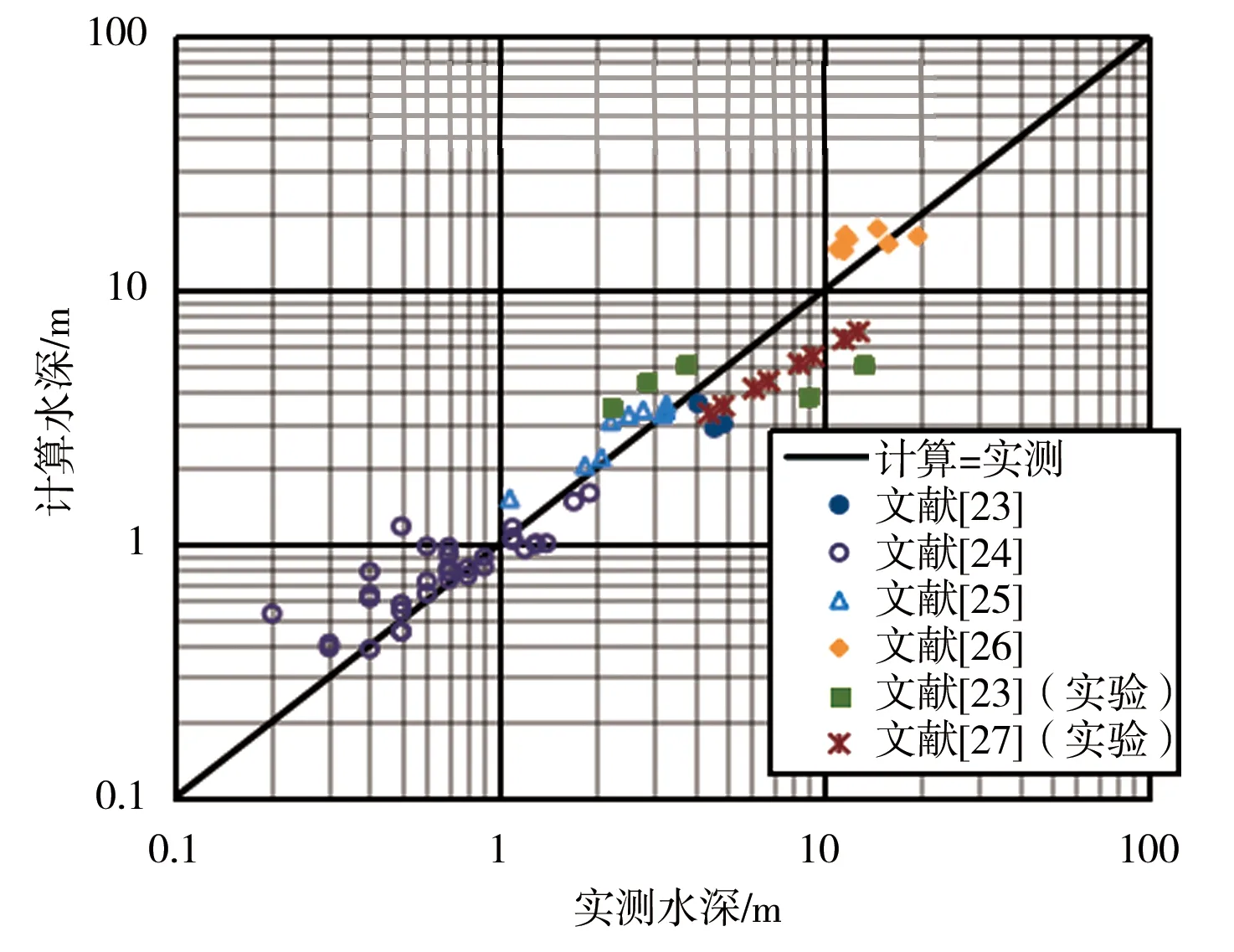
a)式(17)、(18)计算结果

由图3可看出,对于稳定河宽计算,本文式(17)、(18)计算及Yalin和da Silva方法计算结果散点均集中且均匀分布于“计算=实测”直线两侧,表明本文计算公式与Yalin和da Silva方法计算值均与实测值接近。

由图4可看出,对于稳定水深计算,本文式(17)、(18)计算结果散点集中且均匀分布于“计算=实测”直线两侧,表明计算值与实测值接近;而Yalin和da Silva方法对于文献[23]的计算散点分布于“计算=实测”直线下侧,说明计算值小于实测值,其余大部分散点均较均匀集中分布于直线两侧。总体而言,对于稳定水深本文计算公式与Yalin和da Silva方法计算值均与实测值接近。

以上是通过散点分布情况定性比较检验,为定量检验本文公式计算精度,需采用误差指标进行对比。闫志方等[30]在比较溢洪道宽顶堰流量系数公式时采用了差异比(DR)、相对误差(RE)、几何平均偏差(GAD)3个指标,本文将采用这3项指标来分析比较计算值与观测值之间的误差。指标计算见式(19)—(21):

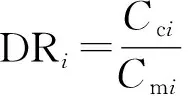
(19)

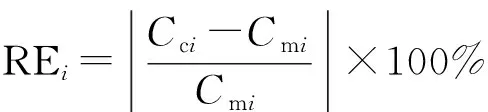
(20)

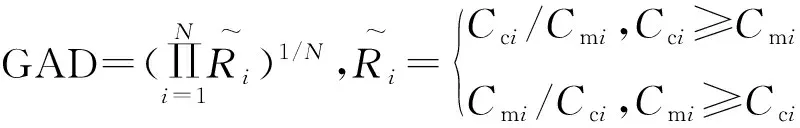
(21)

式中Cc——计算值;Cm——实测值;N——数据组数。

DR越接近1表示计算值与观测值越接近;RE越接近0表示计算值与观测值越接近;GAD越接近1表示计算值与观测值越接近。

经计算,本文式(17)、(18)与Yalin和da Silva方法计算结果的平均相对误差、平均差异比以及几何平均偏差对比见表5。

表5 本文公式与Yalin和da Silva方法误差指标比较

由表5误差指标比较可得出以下结论。

a)本文公式计算河宽和水深的平均相对误差分别为36.6%和30.3%,Yalin和da Silva方法计算河宽和水深的平均相对误差分别为38.7%和31.4%,本文公式计算河宽和水深的平均相对误差略低。

b)本文公式计算河宽和水深的平均差异比分别为1.18和1.09,Yalin和da Silva方法计算河宽和水深的平均相对误差分别为1.20和1.04。对于河宽的计算,本文公式计算结果更接近于实测值,而对于水深计算Yalin和da Silva方法计算结果更接近实测值。

c)本文公式计算河宽和水深的几何平均偏差分别为1.37和1.33,Yalin和da Silva方法计算河宽和水深的平均相对误差分别为1.42和1.38。对于河宽和水深的计算,本文公式计算结果更接近于实测值。

综上分析,总体而言本文公式计算结果的误差指标略优于Yalin和da Silva方法,但从各误差指标的数值上看2种方法差别不大,可认为2种方法计算精度相当。因此,可将本文公式应用于河道防洪、渠道设计、河道整治、航运码头建设等工程实践当中。

4 结论

a)基于量纲分析理论找出了稳定河道水力几何形态的影响参数Π1和Π2,可将稳定河宽BR和稳定水深hR分别表达为BR/D=fB(Π1,Π2)和hR/D=fh(Π1,Π2),原型观测和水槽试验资料作为样本数据进行线性回归分析,得出稳定河宽BR和稳定水深hR的表达式。

b)对比本文公式及Yalin和da Silva方法计算的河宽散点图,2种方法计算值均与实测值接近;对比两者计算的水深散点图,本文公式计算值与实测值接近,而Yalin和da Silva方法少量散点计算值小于实测值,其余大部分散点均较均匀集中分布于直线两侧。总体而言,本文计算公式与Yalin和da Silva方法计算的河宽和水深值均与实测值接近。

c)对比各误差指标,总体而言本文公式计算结果略优于Yalin和da Silva方法,但从各误差指标的数值上看2种方法差别不大,可认为两者计算精度相当,故可将本文公式应用于工程实践当中。