数学直观和数学思维在解题中的应用

孔令磊

(湖北省武汉市华中科技大学同济医学院附属中学)

数学解题中,数学直观是基于数感、量感、符号意识、结构意识、几何直观等建立起来的一种数学抽象能力,它影响着解题方案的拟定,是解题的核心.数学思维是基于运算能力、推理意识而建立起来的逻辑推理能力,它影响着解题目标的达成,是解题的基础.发展数学直观、锻炼数学思维是复习备考中培养综合应用能力,提升素养水平的集中体现.笔者以一道联考试题的解法探究为例,剖析数学直观和数学思维在数学解题中的应用.

一、试题调研

【例题】若x,y∈R,4x2+y2+xy=1,则当x=________时,x+y取得最大值,该最大值为________.

从高三学生质量分析数据看,有42%的学生能够做对.笔者对回答正确的学生调研,发现主要涉及五种解题视角,根据使用的方法进行统计,结果如表所示:

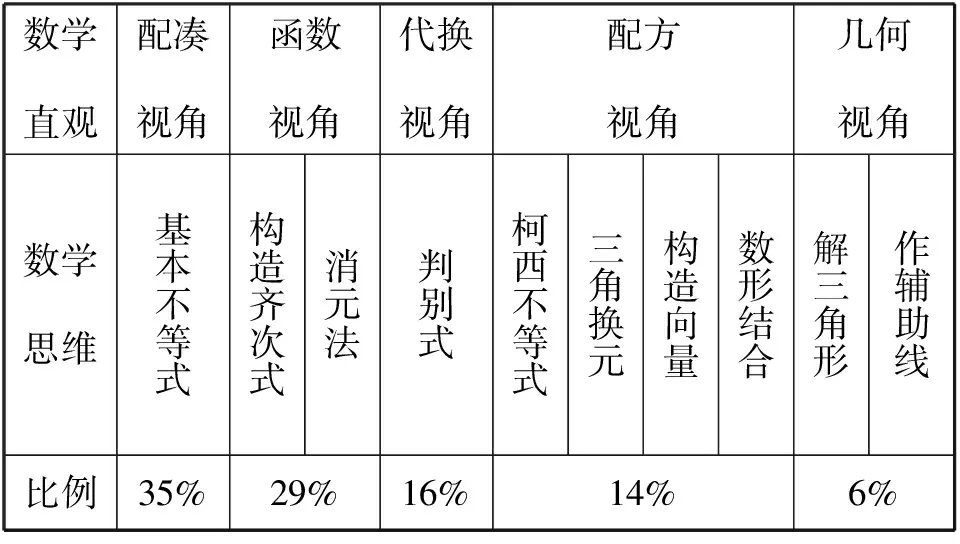
数学直观配凑视角函数视角代换视角配方视角几何视角数学思维基本不等式构造齐次式消元法判别式柯西不等式三角换元构造向量数形结合解三角形作辅助线比例35%29%16%14%6%

二、解法剖析

1.配凑视角

适当地进行配凑,运用基本不等式解题,是学生运用最多的方法.这既符合教师对新教材中基本不等式内容的把握,也体现出学生对此类问题的第一感,但配凑出有效的结构是解题的难点.

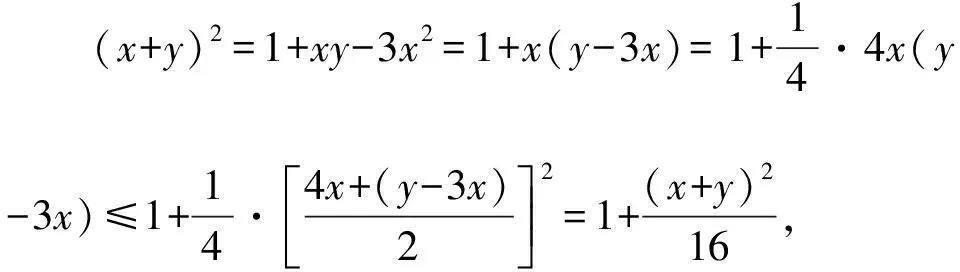
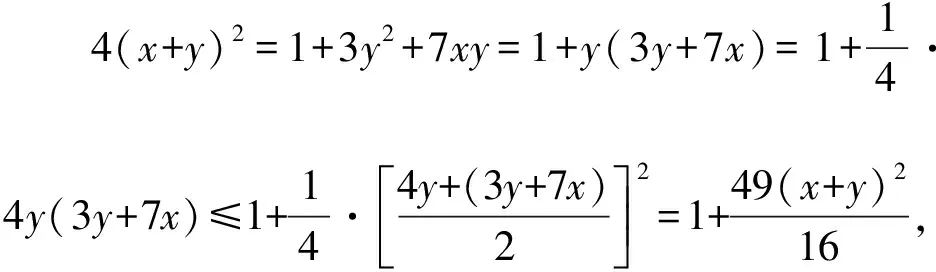
2.函数视角

建立函数是解决最值问题常用的方法,在二次型条件下常见的策略有:构造齐次式,通过换元得到一元函数;引入极坐标,得到关于θ的函数;消元处理,得到关于一个变量x的函数.目标函数的建立及其最值的求解,往往有比较大的计算量,需要学生有一定的计算能力.

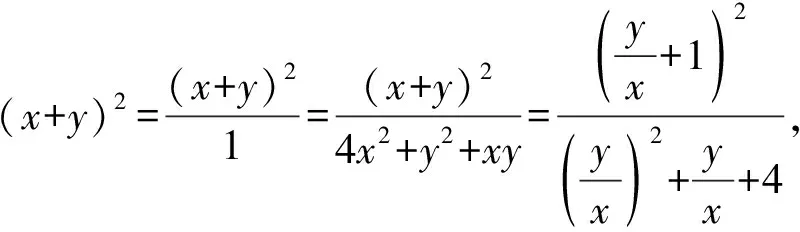
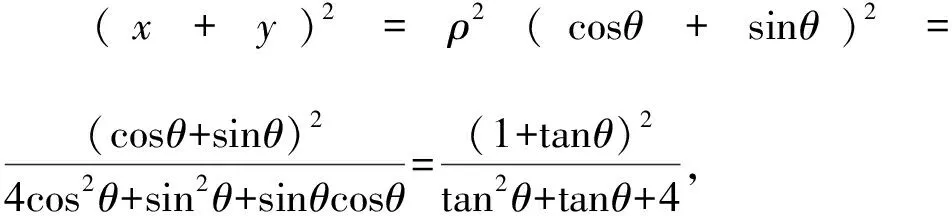
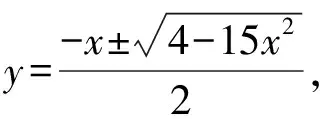
3.代换视角

问题转化是解题的关键,有效地转化可以把较难解决的问题化为较易解决的问题.题设中有二次型条件,可以整体代换后构造二次方程,通过方程有解条件(即利用一元二次方程根的判别式)转化问题,建立不等式.从调研数据看,由代换视角入手解答正确的同学并不是很多.在教学的过程中,教师需要把问题转化的思维过程暴露出来,引发学生要多思考:如何转化?为什么可以这样转化?

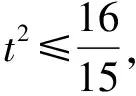
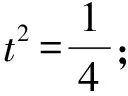
4.配方视角

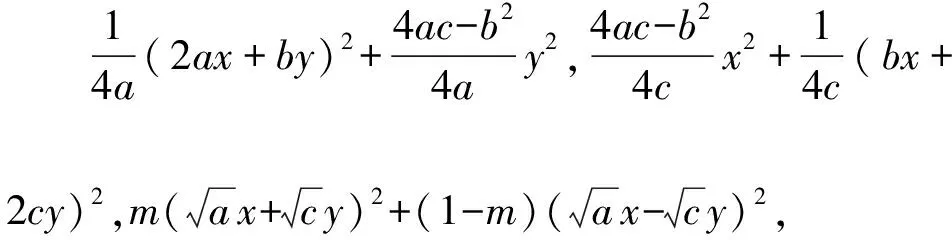
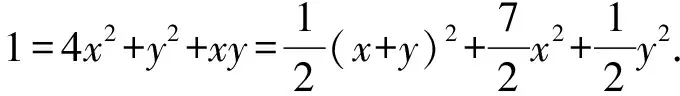
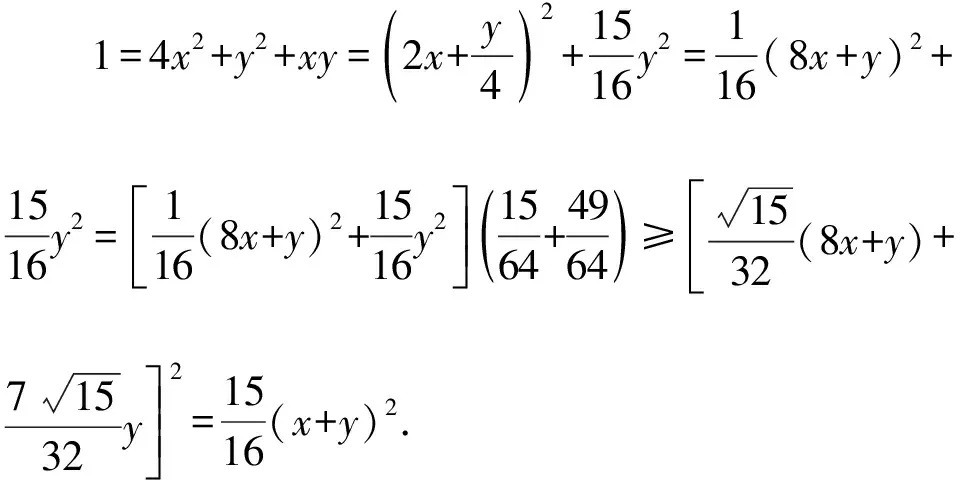
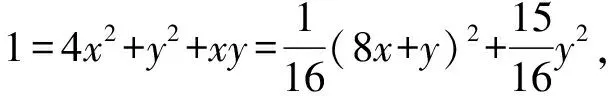
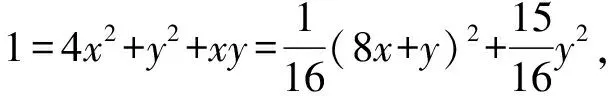
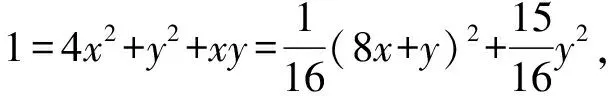
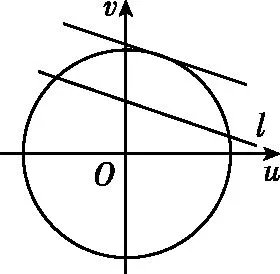
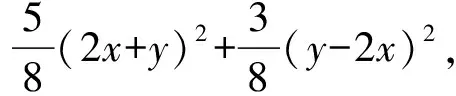
5.几何视角

由二次型结构的特征联想到余弦定理,构造三角形,给题设条件和求解目标赋予几何意义,则问题变为定边对定角下三角形相关的最值问题.

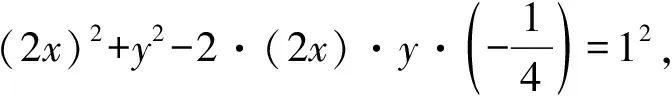
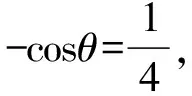
三、教学启示