基于实时数字仿真系统的同群光伏系统等值建模研究

2023-12-06王建安祝文军邹强李钢黄如海

宁夏电力 2023年6期

王建安,祝文军,邹强,李钢,黄如海

(1.南京南瑞继保电气有限公司,江苏南京 211102;2.青海陕煤新能源科技有限公司,青海西宁 810001)

0 引言

光伏系统的光伏单元数量很多,随着并网容量的增加,其动态特性将对电力系统产生较大影响。使用实时数字仿真系统(real time digital simu-lation,RTDS)研究光伏系统的电磁暂态特性时,若搭建成百上千台光伏单元的详细模型,过高的运算阶数和仿真实时性的要求将会消耗巨大的仿真资源,从而给建模仿真带来困难[1]。通常在考察整个光伏系统并入交流电网的动态特征时,可将光伏系统等效为一个整体进行建模,只须等值模型能准确模拟PCC点各频段的动态特性[2-6]。建立等值模型的一般步骤是先对站内的光伏单元按照一定的准则进行分群,再对同群的单元进行等值,风电场、储能站的等值与光伏系统的等值方法相同[7-9]。本文基于RTDS电磁暂态仿真平台,以同群光伏系统为研究对象,其研究结果和结论将为风电、储能的电磁暂态等值建模提供积极的参考。该方法旨在对光伏系统的所有光伏单元进行等值,忽略了集电线路及厂站内其他电力电子设备的影响,该法使用的前提条件是各光伏单元具有同调性,即一次系统结构及参数、控制系统、外部环境(光照强度、温度)等均相同。

本文从以下方面进行研究:1)分别给出倍乘和聚合两种等值原理,分析倍乘和聚合两种方法的准确性和优缺点;2)搭建多台光伏单元的RTDS详细多机模型作为参考,搭建倍乘和聚合的RTDS等值模型;3)分别在两种不同系统短路容量下,通过故障穿越、有功阶跃、频率偏移等试验以及阻抗频率扫描进行仿真验证。

1 倍乘等值

RTDS中有一类变压器采用贝杰龙传输线原理建模,基于该原理可实现功率倍乘。倍乘时,特征阻抗减小N倍,原边电流增大N倍,从而功率增大N倍。在不改变变压器阀侧光伏单元输出特性的基础上,按倍乘系数放大变压器网侧输出功率,可实现用1台光伏模型等值多台相同工况光伏单元模型的目的。功率倍乘如图1所示。

图1 光伏系统倍乘

倍乘变压器采用接口传输线原理,相对于常规变压器建模原理,引入一个虚拟对地电容,如图2所示。图2中Lsys为系统电感。

图2 倍乘模型结构

虚拟电容与变压器的短路电感满足以下关系:

(1)

式中:Cfic是虚拟电容值,ΔT是仿真主步长,Ltr是变压器短路电感。

根据变压器电气参数,可得:

(2)

式中:VLLrated是PCC母线额定电压,f0是基波频率,NStr是变压器倍乘后容量,Xrt*是变压器短路电抗标幺值。

定义虚拟电容无功标幺值为Qfic*,可得:

(3)

综合以上公式,可得:

(4)

本文案例采用的是RTDS通用换流器模型(universal converter model,UCM),UCM对接收的脉冲进行改进,可支持高频开关器件在主步长(约50 μs)运行仿真。

假设Xrt*为0.1,f0为50 Hz,ΔT=50 μs,且网侧电压VLL运行在额定电压VLLrated,可计算出Qfic*=0.247%。

由上述推导可知,该虚拟电容引入的基波无功功率占比很小,通常可以忽略,但该电容对高频阻抗特性的影响需要关注。

2 聚合等值

基于变压器阀侧变流器输入阻抗不变的原则,不改变变流器一次系统及控制系统参数,如图3所示,保持聚合前后Zvsc不变,通过改变变压器变比以提升副边电压的方式,实现原边输入阻抗是聚合前的1/N。

图3 聚合模型等效电路

等效电路中,Zin、Zt、V2与Zin′、Zt′、V2′分别为变压器聚合前后的输入阻抗、短路阻抗、副边电压。

聚合前的阻抗:

(5)

聚合后的阻抗:

(6)

变压器容量由Str聚合到NStr,聚合前后不改变变压器阻抗标幺值,可得

Zt′=Zt/N

(7)

根据等值条件

Zin′=Zin/N

(8)

可得

(9)

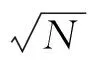
3 光伏系统等值建模与验证分析

3.1 RTDS等值建模

基于RTDS实时数字仿真平台,以容量30 MW的光伏系统为例,分别搭建30台单机1 MW的参考模型、1台30 MW倍乘模型及1台30 MW聚合模型。参考模型由30台结构相同的1 MW光伏单元组成,分别经30台变压器并入交流系统。倍乘模型在单机1 MW的基础上将变压器倍乘系数设置为30后并入交流系统,聚合模型以1台30 MW光伏单元经变压器并入交流系统。3个模型的一次系统结构、控制策略及控制参数、光照和温度条件均相同。光伏并网系统如图4所示。

图4 光伏并网系统

图4中,光照和温度是光伏单元的外部变量输入,Udc为变流器直流侧电压。建立光伏阵列模型,通过最大功率跟踪(maximum power point tracking,MPPT)算法计算其最大功率点电压作为变流器直流电压控制的参考值。

变流器控制方式为直流侧定直流电压、交流侧定无功控制。一次系统元件参数及运行参数如表1—表4所示。

表1 光伏单元电气参数

表2 变流器电气参数

表3 变压器电气参数

表4 等值前后主要运行参数

3.2 仿真验证分析

3个模型的光伏变流器解锁后均运行满功率30 MW,分别在强系统和弱系统下进行仿真验证,强系统短路比(short circuit ratio,SCR)是5,弱系统SCR是2。验证试验包括故障穿越(分为高、低电压穿越)、有功阶跃、频率偏移。观测对象是3个模型的网侧A相电压、A相电流、有功功率、无功功率及系统频率。

3.2.1 高电压穿越

图5、图6分别是SCR=5和SCR=2时的高电压穿越试验波形,设置网侧PCC电压由1.0 p.u.抬升至1.2 p.u.,经300 ms后恢复至1.0 p.u.。

图5 高电压穿越试验(SCR=5)

图6 高电压穿越试验(SCR=2)

3.2.2 低电压穿越

图7、图8分别是SCR=5和SCR=2时的低电压穿越试验波形,设置网侧PCC电压由1.0 p.u.跌落至0.2 p.u.,经300 ms后恢复至1.0 p.u.。

图7 低电压穿越试验(SCR=5)

图8 低电压穿越试验(SCR=2)

3.2.3 有功阶跃

图9、图10分别是SCR=5和SCR=2时的有功阶跃试验波形,设置有功指令由1.0 p.u.跌落至0.2 p.u.,经300 ms后恢复至1.0 p.u.。

图9 有功阶跃试验(SCR=5)

图10 有功阶跃试验(SCR=2)

3.2.4 频率偏移

图11、图12分别是SCR=5和SCR=2时的频率偏移试验波形,设置系统频率由50 Hz下降至49.5 Hz,300 ms后恢复至50 Hz,经200 ms之后,系统频率由50 Hz上升至50.5 Hz,300 ms后恢复至50 Hz。

图11 频率偏移试验(SCR=5)

图12 频率偏移试验(SCR=2)

经不同系统短路容量下4个暂态试验的验证,从波形可以看出三个模型的暂态特性基本相同,其中聚合模型与参考模型的暂态特性曲线高度重合,而倍乘模型与参考模型的无功功率曲线略有偏差,主要因虚拟电容的引入带来了影响。

4 阻抗频率特性分析

故障穿越、有功阶跃及频率偏移等试验主要体现光伏系统在工频下的暂态特性,但在研究光伏接入柔直的稳定性问题时(如接入孤岛柔直后的稳定性),光伏系统的阻抗频率特性显得尤为重要[10-11]。基于dq阻抗扫描方法对模块化多电平换流器(modular multilevel converter,MMC)的阻抗频率特性进行分析[12]。相较于序阻抗理论,dq阻抗分析方法与实际系统的物理环节联系更加紧密,有利于定量分析外部阻抗特性与内部控制环节之间的关系。考虑基波三相平衡的交流系统在同步旋转坐标系下存在直流静态工作点,可基于周期平均模型在稳态工作点进行线性化处理,建立并网变流器在同步旋转坐标系下的小信号模型,dq阻抗表征了同步旋转坐标系下并网变流器外端口小信号电压和电流的关系,如式(10)表示。

(10)

式中:ΔUd、ΔUq为端口dq域小电压信号;Δid、Δiq为端口dq域小电流信号;Zdd(s)、Zqq(s)分别为d轴、q轴阻抗,Zdq(s)、Zqd(s)为耦合项。

采用RTDS的谐波阻抗扫描元件分别对参考模型、倍乘模型及聚合模型PCC点的电压源换流器(voltage source converter,VSC)侧进行阻抗扫描,从PCC点采集三相电压电流,扫描分析结果如图13所示。

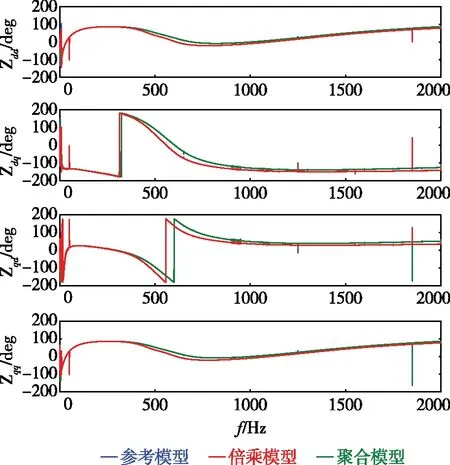
(b)相频特性图13 三个模型的阻抗频率特性

从扫描结果可以看出,倍乘模型与参考模型的频率阻抗特性在低频段(300 Hz以下)重合度较高,而在高频段(300 Hz以上)有明显的偏差;聚合模型与参考模型的阻抗特性在整个频段完全一致(图中蓝线与绿线完全重合)。扫描结果印证了聚合模型比倍乘模型具有更高的等值精度,因此聚合等值方法更适用于光伏系统接入柔直的阻抗频率稳定性研究。