Study of the gluonic quartic gauge couplings at muon colliders

Ji-Chong Yang ,Yu-Chen Guo,* and Yi-Fei Dong

1 Department of Physics,Liaoning Normal University,Dalian 116029,China

2 Center for Theoretical and Experimental High Energy Physics,Liaoning Normal University,Dalian 116029,China

Abstract The potential of muon colliders opens up new possibilities for the exploration of new physics beyond the Standard Model.It is worthwhile to investigate whether muon colliders are suitable for studying gluonic quartic gauge couplings (gQGCs),which can be contributed by dimension-8 operators in the framework of the Standard Model effective field theory,and are intensively studied recently.In this paper,we study the sensitivity of the process μ+ μ - →jjνto gQGCs.Our results indicate that the muon colliders with c.m.energies larger than 4 TeV can be more sensitive to gQGCs than the Large Hadron Collider.

Keywords: gluonic quartic gauge coupling (gQGC),effective field theory (EFT),muon collider,Vector Boson Fusion (VBF)

1.Introduction

So far,most experimental results have demonstrated the success of the Standard Model (SM).However,the theoretical difficulties of the theory itself have led people to believe that the SM is merely an effective theory,with the expectation of new physics (NP) potentially emerging at higher energy scales[1].Due to the lack of clear signs of new physics,the SM effective field theory (SMEFT) [2–5] has become a popular theoretical tool for studying experimental results in a modelindependent way.In most cases,NP effects are expected to manifest in physical processes that are described by dimension-6 operators of SMEFT.However,in some special cases,the contribution of dimension-8 operators may be more important [6–11].These cases include anomalous quartic gauge coupling (aQGC) and neutral triple gauge coupling(nTGC),which have been the subject of many theoretical studies and experimental measurements [12–42].These couplings are fixed by electroweak gauge bosons only.Another type of anomalous gauge coupling that does not exist in the SM is the quartic coupling between gluons and electroweak (EW) vector bosons.They can be described by dimension-8 operators,which are operators contributing to gluonic quartic gauge couplings (gQGCs) [7].The quartic couplings of gluons to EW gauge bosons arise in the Born–Infeld (BI) extension of the SM,which was originally proposed to set an upper limit on the strength of the electromagnetic field [6].It has been shown that the BI also appears in the theories inspired by M theory [43–45].Recently,the gQGCs have been studied at the Large Hadron Collider (LHC)[7,46].

High-energy collisions can directly generate new particles,while precise measurements assist us in identifying the indirect effects of unknown new physics and understanding the dynamics of known particles.The muon collider capitalizes on the advantages of two strategic approaches to exploit the complementarity between energy and precision.The inception of concepts pertaining to muon colliders dates back to earlier time [47–51].At present,the energy frontier attainable by muon colliders remains undetermined.Ongoing investigations are centered on a 10 TeV configuration,with a targeted integrated luminosity of 10 ab-1[52,53].With the high energy and high luminosity,the muon collider not only possesses a stronger capability for probing NP compared to the LHC but also has the ability for more precise measures.As a result,high-energy muon colliders have gained much attention in the community [38–41,54–64].The muon colliders are ideal places to study the dimension-8 operators,including those contributing to the gQGCs.In a high-energy muon collider,the initial state muons emit low-virtuality vector bosons.The weak-boson fusion process transforms the muon collider into a high-luminosity vector boson collider[52,65].The gQGCs can affect the processμ+μ-→jjνvia both the vector boson fusion (VBF) processes and the triboson productions.In this paper,we study the sensitivity of the processμ+μ-→jjνto the gQGCs.

Figure 1.The Feynman diagrams of the gQGC contributions. The tri-boson contribution is shown in the left panel,while the VBF contribution is shown in the right panel.

The rest of this paper is organized as follows.In section 2,the dimension-8 operators contributing to gQGCs are introduced.In section 3,we compare the VBF process with the tri-boson process and discuss the unitarity bound on the operator coefficients.We also present our event selection strategy at muon colliders with different energies and luminosities.The numerical results of the constraints on the coefficients are presented in section 4.In section 5,we summarize and draw our conclusions.

2.Dimension-8 gluonic QGC operators

Although there are many possibilities for new physics at higher energy scales above the EW one,the low energy effective field theory (EFT) should be subject to the SM SU(3)c× SU(2)L× U(1)Ygauge symmetries.A convenient way to take these symmetries into account is the SMEFT [66],which includes systematically all the allowed interactions with mass dimension d ＞4.The extra dimensions are compensated by inverse powers of a mass scale M that is associated with heavy new particles.The gQGCs appear at dimension-8 level with 1/M4suppression [7],

The total and differential cross-sections are largely determined by the Lorentz structure of the gQGC operators.The eight operators can be classified into four pairs {OgT,(0,4),OgT,(1,5),OgT,(2,6),OgT,(3,7)},each with a same Lorentz structure.

The hierarchical structure of the cross-sections generated by the eight gQGC operators is manifest in the 95% C.L.lower bounds derived from the ATLAS data [7] are

3.Features of the signal

3.1.Compare of the tri-boson process and the VBF process

The gQGCs can contribute to the processμ+μ-→jjνvia both the VBF and tri-boson processes,the Feynman diagrams are shown in figure 1.When a new particle X presents in the final states,the relative scaling between the VBF and annihilation contribution is [67]

Thousands of lights were burning on the green branches, and gaily-colored pictures, such as she had seen in the shop-windows, looked down upon her. The little maiden stretched out her hands towards them when--the match went out. The lights of the Christmas tree rose higher and higher, she saw them nowas stars in heaven; one fell down and formed a long trail of fire.

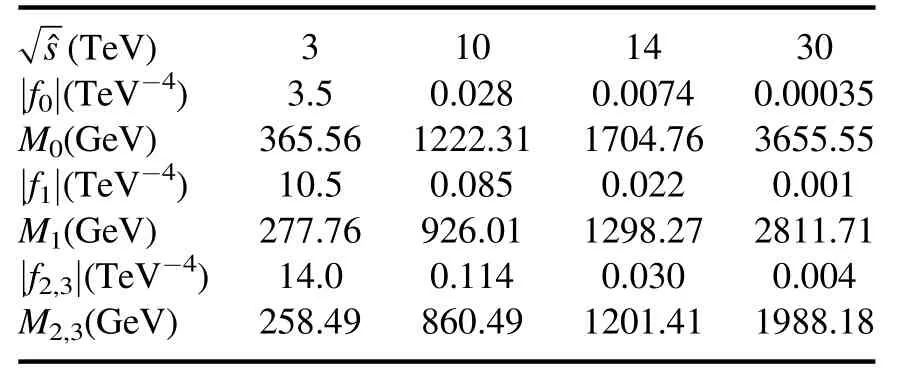
Table 1.The upper bounds of coefficients |fi| and lower bounds of Mi in the sense of partial wave unitarity at different energies.

Figure 2.σtri in equation (4) compared with σVBF in equation (5).When ＜ 5 TeV,σtri is larger than σVBF.

The numerical results of equations (4) and (5) are shown in figure 2.The detector simulation is not included until the Monte Carlo (MC) simulation is applied.It can be seen that the tri-boson contribution is larger than the VBF at about＜ 5 TeV,at=30 TeV,σVBFis about 5 times of σtri.Therefore the contribution of tri-boson is not negligible.In this paper,σVBF,σtri,and the interference between them are considered as the signal of the gQGCs.

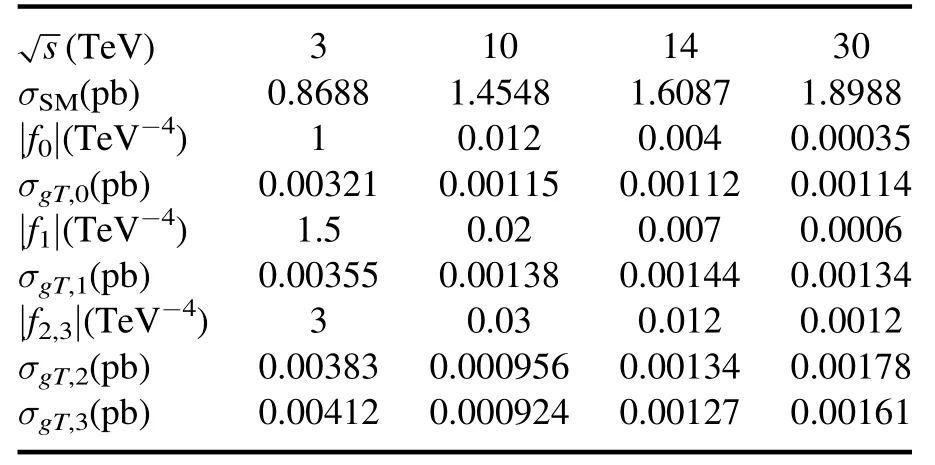
Table 2.The cross-sections of the SM contribution and the upper bounds of coefficients |fi| used in the phenomenological study.The cross-sections of the gQGCs are also shown.

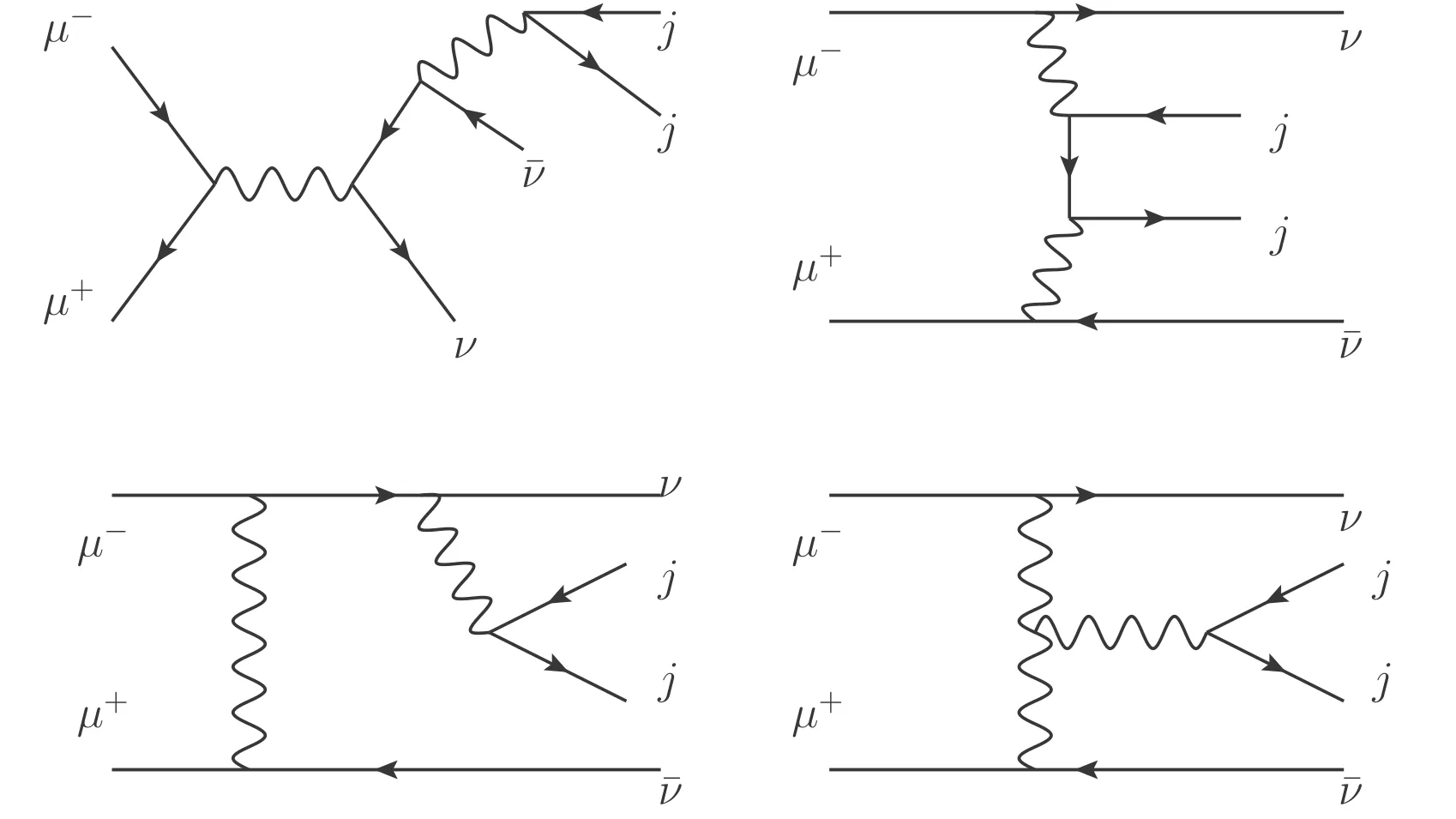
Figure 3.Typical Feynman diagrams of the SM contribution.

Apart from that,note that OgT,4,5,6,7operators do not contribute to the W-boson fusion processes.Since the energies considered are mainly above 5 TeV,in this paper,we only consider the contributions of the OgT,0,1,2,3operators.However,we shall emphasise that the process WW →gg provides a chance to study the OgT,0,1,2,3operators separately,compared with the pp →γγ and pp →Zγ processes where the contributions from OgT,iand OgT,i+4are proportional to each other [46].

3.2.Unitarity bound

The SMEFT is not UV completed.As an EFT,the SMEFT is only valid under a certain energy scale.One of the signals when the SMEFT is no longer valid is the violation of unitarity.With dimension-8 operators,the amplitude of the process W+W-→gg grows as ˆs2which leads to the violation of unitarity [71–73] at large enough energy.The partial wave unitarity bound [74–76] is often used to check whether the energy scale considered is already invalid.For the subprocesswhere λicorrespond to the helicities,the amplitude can be expanded as [77]

where λ=λ1-λ2,λ′=λ3-λ4,θ and φ are zenith and azimuth angles of the one of the gluons in the final state,respectively,andare Wigner d-functions [77].The partial wave unitarity bound is |TJ| ≤2 [74] which is widely used in previous works [33,35–39,78–81].

At leading order of ˆs,the relevant helicity amplitudes are

There are other helicity amplitudes which lead to same unitarity bounds as those derived from equation (8),and therefore are not presented for simplicity.Assuming one operator at a time,the tightest bounds are

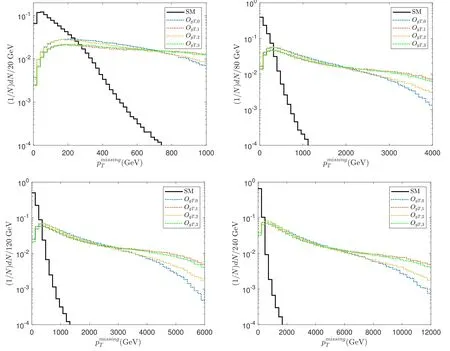
Figure 4.The normalized distributions of for the SM and gQGCs at different energies.The top left panel corresponds to=3 TeV,the top right panel corresponds to=10 TeV,the bottom left panel corresponds to =14 TeV,and the bottom right panel corresponds to =30 TeV.

As such,for the subprocess W+W-→gg,≤s,we consider the largest possiblethe unitarity bounds on the coefficients at different energies are listed in table 1.The energies are chosen as the muon colliders [52,53].

3.3.Event selection strategy

The typical Feynman diagrams for the background at tree level are shown in figure 3.An important feature is that the two jets are both from quarks,which is different from the case of gQGCs where the two jets are both from the gluons.As a consequence,there is no interference term between the SM and the gQGCs.Once the efficiencies of the event selection strategy for both the background and the signal are obtained,the cross-section can be read out.

The signal events are generated by assuming one operator at a time.The sensitivity of the processμ+μ-→to the gQGCs can be estimated with respect to the significance defined as [87,88]

Figure 5.Same as figure 4 but for mjj.

where Ns=NaQGC-NSMand Nbg=NSM.The Nbgcan be obtained by σSMand the luminosities of the muon colliders,where the Nscan be provisionally estimated using σtri+σVBFwhere σtriand σVBFare given in equations (4) and (5).The coefficients are chosen so that the signal significance of the VBF contributions are about Sstat=2～3 before cuts at luminosity L=1 ab-1,L=10 ab-1for=3 TeV and≥ 10 TeV,respectively [52,53].The coeffciients at different energies are listed in table 2.Note that they are also chosen to be within the partial wave unitarity bounds in table 1.The contributions of the gQGCs (denoted as σgT,i)obtained by MC are also shown in table 2.

To investigate the kinematic features,we require that the final states contain at least two jets,which is denoted as the Njcut.To suppress the events from the process μ+μ-→jj,we also require a minimalfor the events,whereis the transverse missing energy.can also be used to suppress the events from the SM contribution toμ+μ-→.This is because the signal grows with the energy so that for the tri-boson signal events,the neutrinos are typically from a highly boosted Z boson.Since neutrinos play a role similar to that of the residual jets of the VBF processes at a hadron collider,similar to the standard VBF cut [89],the neutrinos are expected to be back-to-back.For the VBF signal events,although the neutrinos are back-to-back,the nettranspose momentum is still typically larger than the case of the SM.The normalized distributions offor the backgrounds and signals are shown in figure 4.We require the events to have a largewhich is denoted as thecut.

Table 3.The event selection strategies at different energies.

Due to the same reason,for both the tri-boson and VBF signal events,the jets are energetic.As a result,the invariant mass of the hardest two jets (denoted as mjj) should be large for the signal events.The normalized distributions of mjjfor the background and signal are shown in figure 5.We require the events to have a large mjj,which is denoted as the mjjcut.

At different energies,we use different cuts.The event selection strategies are summarized in table 3.The crosssections after cuts are listed in table 4.The efficiencies of the cuts (denoted as ∈) are also shown in table 4.It can be seenthat the event selection strategies can suppress the background significantly.

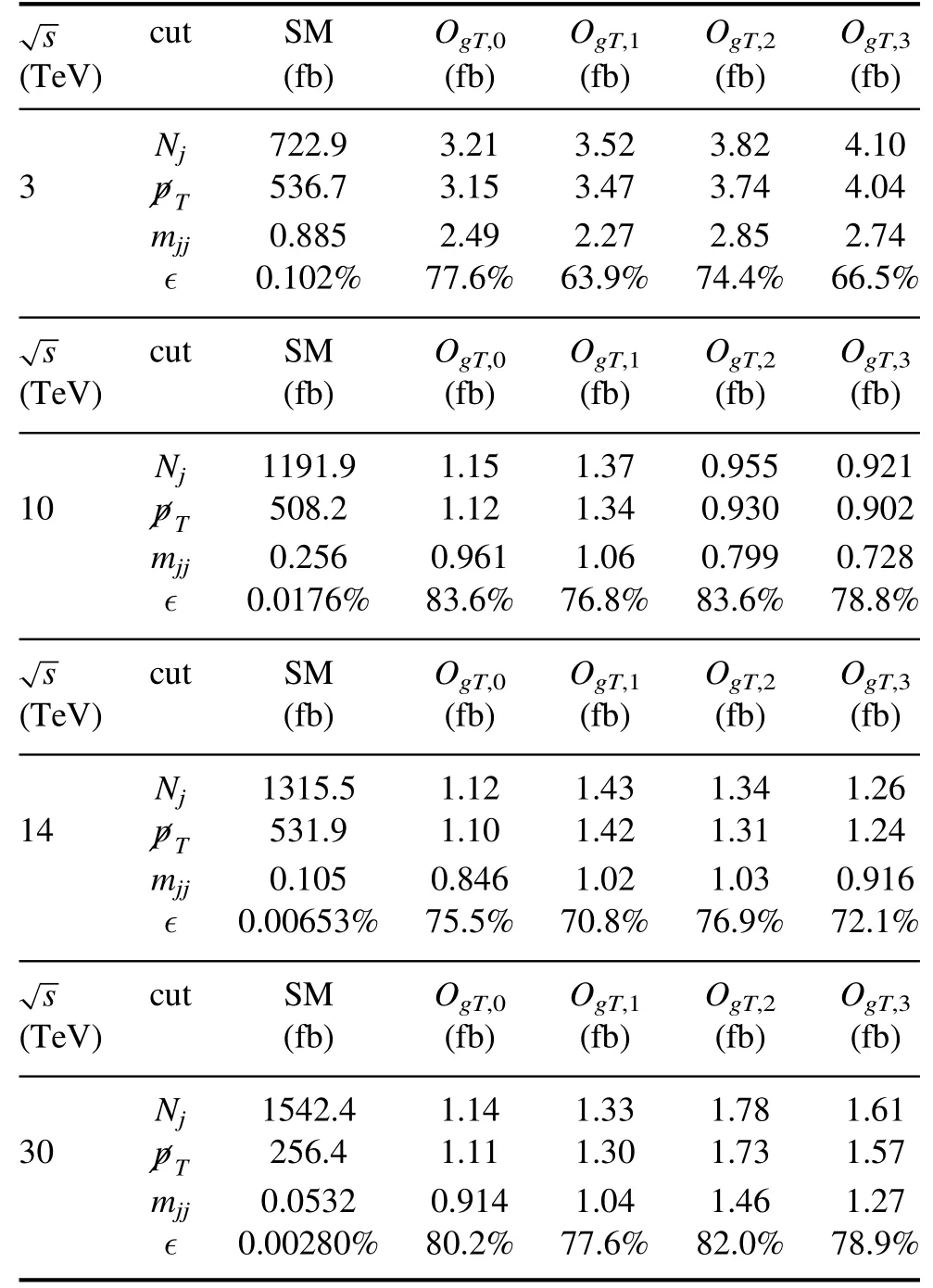
Table 4.The contributions of the SM and gQGCs after cuts.The efficiencies of the cuts are shown in the last row.

4.Constraints on the coefficients

Assuming one operator at a time,without the interference between the SM and the gQGCs,the cross-section after cuts can be expressed as,

where σSMandσgT,iare the cross-sections of the SM and the gQGCs at ˜fi,and ∈SMand ∈gT,iare the cut efficiencies of the SM and gQGC events,respectively.Takingas the ones in table 2,numerical results of σSMand σgT,iare listed in table 2,and ∈SMand ∈gT,iare listed in table 4.The expected constraints at muon colliders can be estimated by the signal significance defined in equation (10).The integrated luminosities for both the ‘conservative’ and ‘optimistic’ cases are considered [52,53].As a result,we can obtain the projected sensitivities on fiand Miby taking 2σ,3σ or 5σ significance.The results are shown in tables 5 and 6.The expected constraints on f2and f3are close to each other,which is indicated by the fact that the leading helicity amplitudes for O2,3are the same.

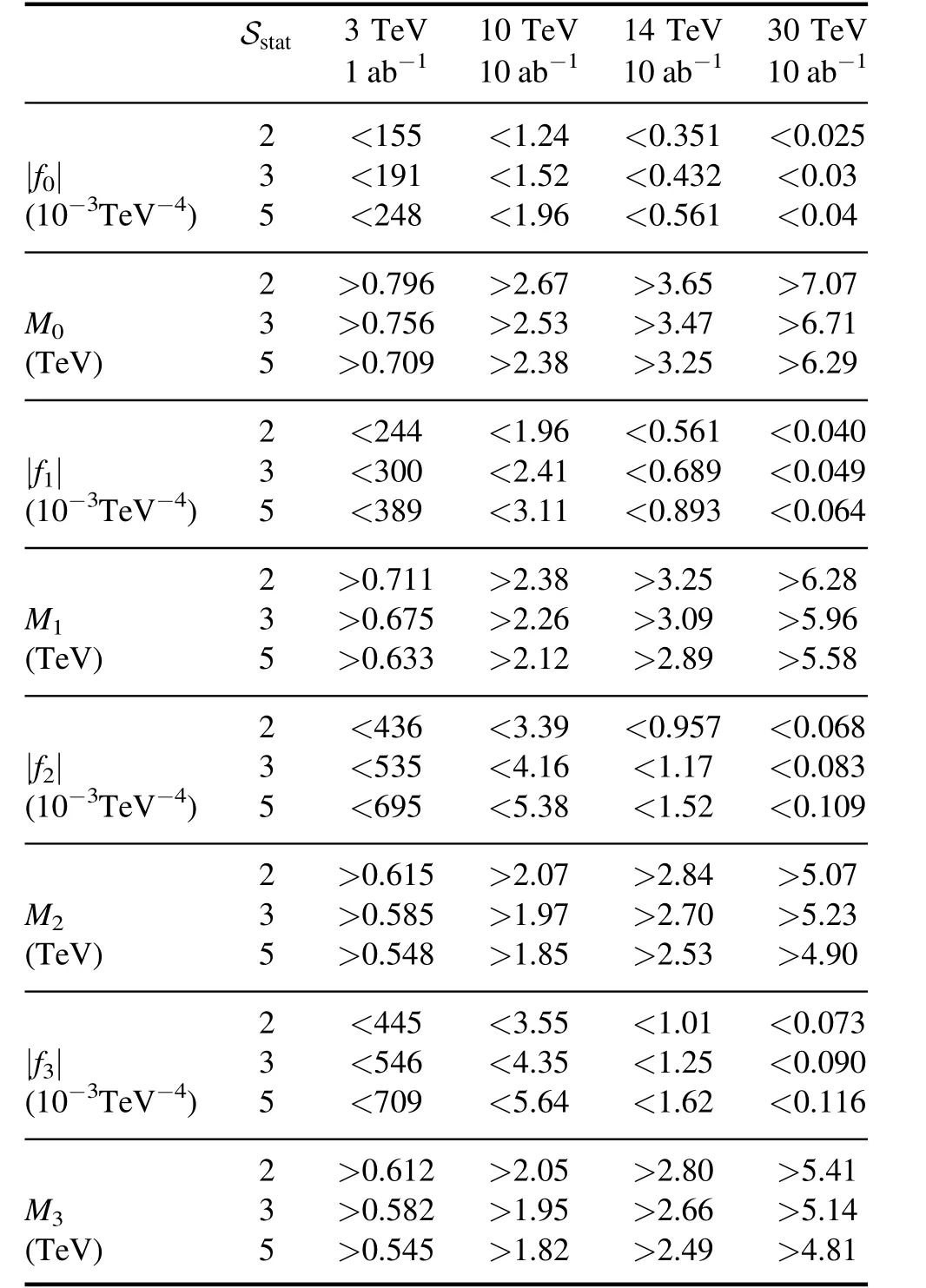
Table 5.The projected sensitivities on the aQGC coefficients at the muon colliders with different c.m.energies and integrated luminosities for the ‘conservative’ case.

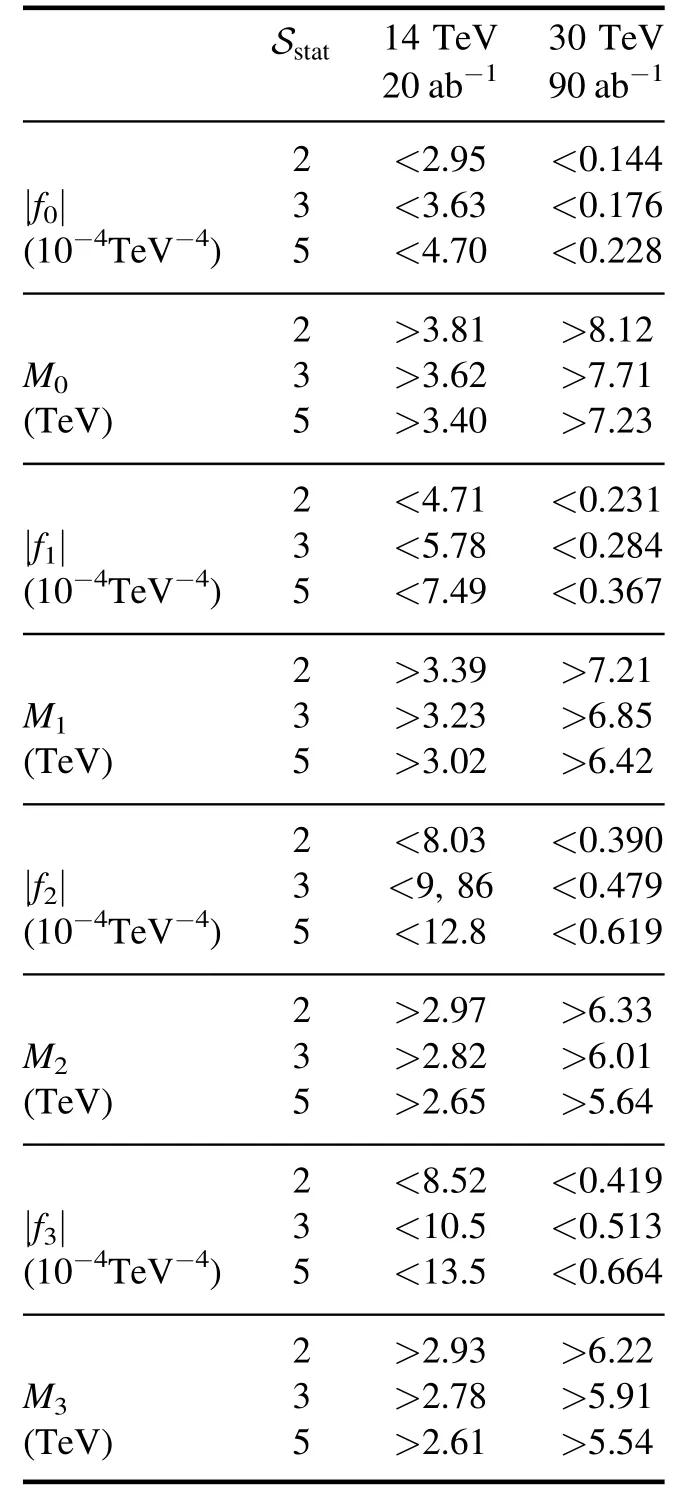
Table 6.The projected sensitivities on the aQGC coefficients at the muon colliders with different c.m.energies and integrated luminosities for the ‘optimistic’ case.

5.Summary

The muon colliders which are also called vector boson colliders are ideal places to study the quartic gauge couplings.In this paper,we investigate the capability of future muon colliders to detect the gQGC in the framework of SMEFT.The cross-sections of the processμ+μ-→with gQGCs present are calculated.

The gQGCs can affect the processμ+μ-→via both tri-boson and VBF contributions.The tri-boson contribution is larger than the VBF whens＜ 5 TeV,and is about 1/5 of the VBF at=30 TeV.Besides,the VBF process can be affected by OgT,0,1,2,3.Therefore,we focus on OgT,0,1,2,3in this paper.

With partial wave unitarity bounds considered,the event selection strategy as well as the expected constraints on the operator coefficients are studied using MC simulation.For the luminosities in the ‘optimistic’ case,2σ lower bounds on M0,1,2,3are about 27%,24%,21% and 20– 21% of the c.m.energies of the muon colliders,respectively.Our results indicate that the muon colliders with＞ 4 TeVcan be more sensitive to the gQGCs than the LHC.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grants Nos.11905093 and 12147214,and the Natural Science Foundation of the Liaoning Scientific Committee No.LJKZ0978.